Конспект урока по алгебре "Кусочно-заданные функции" 9 класс
Урок по алгебре в 9А классе учителя Микитчук Ж.Н. МОУ «СОШ №23»
19.03.07г
Тема урока: «Кусочно-заданные функции»
Цели:
обобщить и совершенствовать знания, умения и навыки учащихся по указанной теме;
воспитывать у учащихся внимательность, сосредоточенность, настойчивость, уверенность в своих знаниях;
развивать мыслительные способности, логическое мышление; речевую культуру, умение применять теоретические знания.
В результате обобщения темы учащиеся должны знать:
понятие кусочно-заданной функции;
формулы различных функций, соответствующие названия и изображения графиков;
уметь:
строить график кусочно-заданной функции;
читать график;
задавать функцию аналитически по графику.
Ход урока
I. Организационно-психологический момент.
Начнем наш урок словами Д.К.Фадеева «Какую бы задачу вы не решали, в конце
вас ждёт счастливая минута – радостное
чувство успеха, укрепление веры в свои силы.
Пусть эти слова на нашем уроке обретут реальное подтверждение.
II. Проверка домашнего задания.
Начнем урок как обычно с проверки д/з.
-Повторите определение кусочной функции и план исследования функций.
1). На доске изобразить придуманные вами графики кусочных функций (рис.1,2,3)
2).Карточки.
№1. Расставьте порядок исследования свойств функций:
выпуклость;
четность, нечётность;
область значений;
ограниченность;
монотонность;
непрерывность;
наибольшее и наименьшее значение функции;
область определения.
№2.Изобразите схематически графики функций:
А) у = kx + b, k0; Б) y = kx![]() , k0;
, k0;
В) у = ![]() , k0.
, k0.
3).Устная работа. – 2мин
Какая функция называется кусочной?
Кусочной называется функция, заданная разными формулами на разных промежутках.
Из каких функций состоят кусочные функции, изображенные на рис.1,2,3?
Какие ещё названия функций вы знаете? Как называются графики соответствующих функций?
Является ли графиком какой-либо функции, фигура, изображенная на рис.4? Почему?
Ответ: нет, т.к. по определению функции, каждому значению независимой переменной х ставится в соответствие единственное значение зависимой переменной у.
4) Самоконтроль -3 мин
Из предложенных графиков и соответствующих формул, задающих функции, выберите верные. Из полученных букв ответов составьте знакомое слово.
Ответ: ГРАФИК
Где в жизни, в науке, в быту мы ещё встречаемся со словом ГРАФИК?
-График зависимости массы от объёма,
-объёма от давления;
- график дежурства;
- график движения поездов;
-графики используются для представления различной информации, например, объём промышленного производства в Саратовской области в период с 1980 по 2002год.. По этому графику можно проследить за снижением и ростом производства в отдельные года.
-Скажите, графиком какой функции представлена данная информация.
Ответ: кусочная функция.
III. Сообщение темы, цели урока.
Тема урока: «Кусочно-заданные функции»
Цель:
- на примере кусочно-заданной функции вспомнить план исследования функций;
повторить шаги построения кусочно-заданной функции;
применять обобщенные знания при решении нестандартных задач.
IV. Актуализация ранее усвоенных знаний.
Понятие функции впервые встретилось нам в 7 классе при изучении линейной зависимости. С точки зрения моделирования реальных процессов, эта зависимость соответствует равномерным процессам.
Пример: Движение пешехода с постоянной скоростью за время t. Формула: s =vt, график – отрезки прямой, расположен в I четверти.
Основная тема 8-го класса – квадратичная функция, моделирующая равноускоренные процессы.
Пример: изученная вами в 9-ом классе формула определения сопротивления нагретой лампы (R) при постоянной мощности (Р) и изменяющемся напряжении (U). Формула
R = ![]() , график – ветвь параболы, расположен-ная в I четверти.
, график – ветвь параболы, расположен-ная в I четверти.
На протяжении трёх лет наши знания о функциях обогащались, количество изученных функций росло, пополнялся и набор заданий для решения которых приходится прибегать к графикам.
Назовите эти типы заданий…
- решение уравнений;
- решение систем уравнений;
- решение неравенств;
- исследование свойств функций.
V.Подготовка уч-ся к обобщающей деятельности.
Вспомним один из типов заданий, а именно – исследование свойств функций или чтение графика.
Обратимся к учебнику. Страница 65 рис.20а из №250.
Задание: прочитать график функции. Порядок исследования функции перед нами.
1. область определения – (-∞; +∞)
2. четность, нечётность – ни четная, ни нечётная
3. монотонность- возрастает [-3; +∞), убывает
[-5;-3], постоянна (-∞; -5];
4. ограниченность – ограничена снизу
5. наибольшее и наименьшее значение функции – унаим = 0, унаиб – не существует;
6. непрерывность- непрерывна на всей области определения;
7. область значений – [0; +∞)
8. выпуклость- выпукла вниз [-5; -2], выпукла и вниз и вверх (-∞; -5] и [-2; +∞).
VI. Воспроизведение знаний на новом уровне.
Вы знаете, что построение и исследование графиков кусочно-заданных функций, рассматриваются во второй части экзамена по алгебре в разделе функции и оцениваются 4-мя и 6-ю баллами. Обратимся к сборнику заданий.
Страница 119 - №4.19-1).
Решение:
1).у = - x![]() , - квадратичная функция, график – парабола, ветви вниз (а = -1, а0).
, - квадратичная функция, график – парабола, ветви вниз (а = -1, а0).
Составим таблицу некоторых значений
х -2 -1 0 1 2
у -4 -1 0 1 4
2) у= 3х – 10, - линейная функция, график – прямая
Составим таблицу некоторых значений
х 3![]() 3
3
у 0 -1
3) у= -3х -10, - линейная функция, график – прямая
Составим таблицу некоторых значений
х -3![]() -3
-3
у 0 -1
4)Построим графики функций в одной системе координат и выделим части графиков на заданных промежутках.
Найдем по графику, при каких значениях х значения функции неотрицательны.
Ответ:f(x) 0 при х = 0 и при ![]() 3
3![]()
VII.Работа над нестандартными заданиями.
№4.29-1), стр. 121.
Решение:
1)Прямая (слева) у = kx + b проходит через точки (-4;0) и (-2;2). Значит,
-4k + b = 0,
-2 k + b = 2; ![]() k = 1, b = 4, у = х+4.
k = 1, b = 4, у = х+4.
Ответ: х +4, если х -2
у = ![]() , если -2 х £ 3
, если -2 х £ 3
3, если х 3
VIII.Контроль знаний.
Итак, подведём небольшой итог. Что мы повторили на уроке?
План исследования функций, шаги построения графика кусочной функции, задание функции аналитически. Проверим как вы усвоили данный материал.
Тестирование на «4»- «5», «3»
I вариант
№1. При чтении графика кусочной функции учащийся допустил три ошибки. Найди эти ошибки и исправь их. Номер ошибки и правильный ответ внеси в таблицу ответов.
У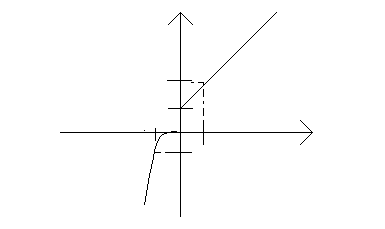
2
1
-1 -1 1 Х
D(f) = [0; +∞)
Ни чётная, ни нечётная
Убывающая (-∞; +∞)
Неограниченная
у наим не существует, у наиб не существует
Непрерывная на всей области определения
Е(f) = (-∞; +∞)
Выпуклая вверх (-∞; 0], выпуклая и вверх и вниз на [0; +∞)
Таблица ответов.
№
ошибки
1
3
6
Правильный
ответ
(-∞; +∞)
Возр-ая
Имеет разрыв
№2. Задай функцию аналитически.
II вариант
№1. При чтении графика кусочной функции учащийся допустил три ошибки. Найди эти ошибки и исправь их. Номер ошибки и правильный ответ внеси в таблицу ответов.
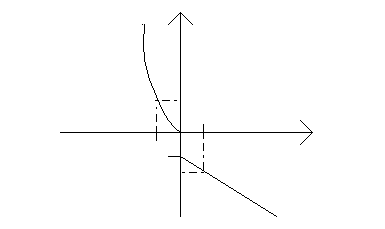
У
1
-1 1 Х
-1
-2
D(f) = [0; +∞)
Ни чётная, ни нечётная
Возрастающая на (-∞; +∞)
Неограниченная
у наим не существует, у наиб не существует
Непрерывная на всей области определения
Е(f) = (-∞; +∞)
Выпуклая вниз (-∞; 0], выпуклая вверх и вниз на [0; +∞)
Таблица ответов.
№
ошибки
1
3
6
Правильный
ответ
(-∞; +∞)
Убыв-ая
Имеет разрыв
№2. Задай функцию аналитически.
- Взаимопроверка
VIII. Анализ и оценка итогов работы
Подведем итог урока.
- Какие функции мы рассматривали сегодня на уроке?
- Какие типы заданий мы обобщили и повторили с помощью кусочно-заданных функций?
- Оценки за урок
IX. Домашнее задание.
Сборник – Iчасть – работа №8, 9 -№16,
II часть - №4.19(2), №4.28(1)
X.Резерв
Творческое задание -задачник – стр 83, домашняя к/р №3 - №2
1 мин
Сл1
8мин
На доске 3 системы координат
Раздаточный материал
№1 – 1 шт + набор на магнитной доске
№2 – 2 шт
На доске 3 системы координат
Сл2
*
Сл3
Сл4
*
Сл5
Сл6
Сл7
Сл8 1 мин
3мин
Сл9
Сл10
Сл11 *
*
*
*
6 мин
Сл12
У доски, показ
*
*
*
*
*
*
*
*
8 мин
Сл13
На доске:
Система координат,
Три функции,
Незаполненные таблицы некоторых значений
*
3 мин
№ записан на доске
Решение одновременно у доски с №4.19
6 мин
Сл15 2 мин
1 мин
Сл16
1мин
Тестирование на «3»
I вариант
№1. Заполните пропуски в плане исследования функции. 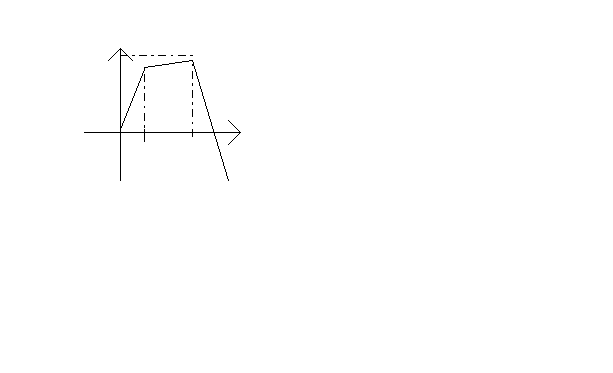
4
0 1 3
D(f) = __________
Ни чётная, ни нечётная
Возрастает на [0;3], убывает на ________
Ограничена ____________
у наим не существует, у наиб =_____
Непрерывна на всей области определения
Е(f) = ____________
Выпукла и вниз и вверх на всей области определения
II вариант
№1. Заполните пропуски в плане исследования функции. 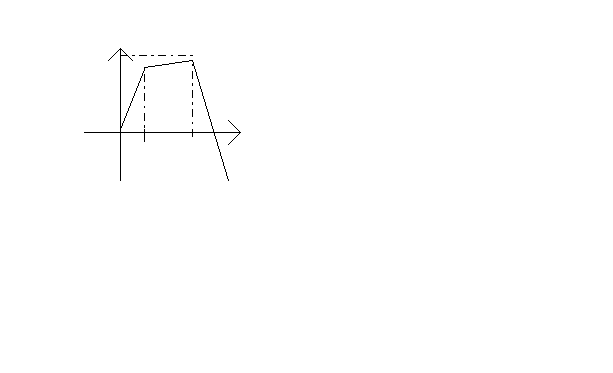
6
0 2 4
D(f) = __________
Ни чётная, ни нечётная
Возрастает на [0;4], убывает на ________
Ограничена ____________
у наим не существует, у наиб =_____
Непрерывна на всей области определения
Е(f) = ____________
Выпукла и вниз и вверх на всей области определения

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ