Логарифмические уравнения

11 класс. Алгебра и начала анализа. А.Г.Мордкович.

Цели урока:

• Обучающие:

  • повторить методы решения логарифмических уравнений;

  • повторить свойства логарифмов;

  • совершенствовать навыков решения логарифмических уравнений.

• Развивающие:

  • развивать логическое мышление;

  • развивать математически грамотную речь.

• Воспитательные:

  • воспитывать познавательную активность, культуру общения;

  • формировать положительную мотивацию к учению.

Ход урока.

1. Организационный момент. (3 мин)

Эпиграф:

Сообщение темы, целей урока.

Каждому ученику дается индивидуальная карточка самоконтроля, в которую на протяжении всего урока он будет записывать количество верных ответов по каждому виду работы.

Индивидуальная карточка самоконтроля

Вид работы

Кол-во верных ответов

Наибольшее кол-во верных ответов

Блиц-опрос

5

Формулы

7

Решение уравнений

3

Сам. работа

3

Итого

18

Критерии оценки:

«5» - 18-17 баллов

«4» - 14-16 баллов

«3» - 9 – 13 баллов

II. Устная работа. (5 мин)

1. 4 ученика вызываются к доске. Им предлагаются логарифмические уравнения в общем виде

1. log _a f (x)=b 2. log _a f (x)= log _a g(x) 3. f (x)^{log a f (x)}=b

4. a(log _n f (x))²+b·log _n f (x)+c=0

и набор карточек, из которых они должны составить решение данного уравнения в общем виде.

log _a f(x)^{log a f(x)} = log _a b

f(x)=a^b

f(x) = g(x)

Пусть t=log _n f(x)

at²+bt+c=0

находим t₁, t₂

log _n f(x)=t_1, log _n f(x)=t₂

f(x)>0

a>0, a ≠1

f(x)>0

a>0, a ≠1

f(x)>0

n>0, n ≠1

f(x)>0

g(x)>0

a>0, a ≠1

В это время классу предлагается блиц-опрос. Каждому ученику дан бланк «Блиц-опрос», в котором он отмечает свои ответы.

1

2

3

4

5

а

б

в

г

Учитель обращает внимание на то, что некоторые вопросы содержат два правильных ответа.

Блиц - опрос

1. Какие из данных функций являются логарифмическими?

а) y= lg (2x+3)

б) y = 4^3x-5

в) y = log ₃ 27 + 8x

г) y = log ₅ 125 – 4x³

2. Область определения логарифмической функции y= log₂ (x-5) +2 :

а) (7; +∞)

б) (5; +∞)

в) (-∞; -5)

г) [5; +∞)

3. Какие из данных функций являются возрастающими?

а) y= log_2.5 (x+7)

б) y = log _0.5 (x-5)

в) y = ln (2x+3)

г) y = log ₂ 4

4. Какая из записей является формулой перехода от логарифмов по основанию m к логарифмам по основанию n:

а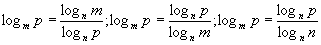) 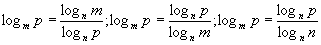б)

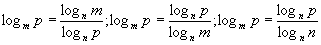
в) ?

5. Свойства логарифмов

У каждого ученика есть аналогичная карточка, необходимо соединить начало и конец формулы.

log _а а n log _а b

log _а а ⁿ 1

log _а b ⁿ n

log _аⁿ b 0

log _а (bc) log _а b - log _а c

log _а (b/c) 1/n · log _а b

log _а 1 log _а b + log _а c

Проверяем правильность выполнения работы. Вносим результат в индивидуальную карточку самоконтроля.

Блиц – опрос

1

2

3

4

а)

х

 

х

 

б)

 

х

 

х

в)

 

х

г)

III. Решение логарифмических уравнений. (15 мин)

Переходим к основной части урока.

На экране – таблица, в которой зашифровано имя ученого, который впервые ввел понятие логарифма. Учащимся предлагается решить уравнения, выбрать наибольший корень и расшифровать закодированное имя. При этом 3 ученика работают у доски, а класс делится на два варианта и каждый вариант решает по два аналогичных уравнения самостоятельно.

Задания на доске:

1. Log₂ (x-3)(x+5)+ Log₂ (x-3)/(x+5) = 2 (1)

2. Lg²x + Lg x +1= 7/ Lg (x/10) (2)

3. x^1-log5^x = 0.04 (3)

Задания для класса:

1 вариант – 1558 (в), 1566(б) (4), (5)

2 вариант – 1565(в), 1563(в) (6),(7)

Кто ввел понятие логарифма?

0,5

1

5

4

25

125

100

0,2

-2

6

10

ж

а

н

р

е

и

п

к

л

д

о

5

6

7

1

1

3

2

3

4

Если уравнения решены правильно, то получаем следующую таблицу

5

6

7

1

1

3

2

3

4

д

ж

о

н

н

е

п

е

р

Джон Непер – шотландский математик, который впервые ввел понятие логарифма. Логарифм – «логос» – соотношение, «арифмос» - число

Результаты работы учащиеся записывают в индивидуальную карточку самоконтроля.

IV. Математический софизм. (3 мин)

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки

Мартин Гарднер

Учащимся предлагается “доказательство” неравенства 2 > 3, необходимо найти ошибку.

Логарифмическая комедия
«2 >3»

Рассмотрим неравенство

¼ > ⅛

(½)² > (½)³

Прологарифмируем по основанию 10

lg (½)² > lg (½)³

2 lg (½) > 3lg (½)

Разделим обе части неравенства на lg (½)

2 >3

V. Самостоятельная работа. (8 мин)

№1552

№1554

№1556

I

а

а

а

II

б

б

б

III

в

в

в

IV

г

г

г

Учащиеся проверяют самостоятельную работу, заносят результат проверки в индивидуальную карточку самоконтроля.

№1552

№1554

№1556

I

2; 9

8; 2

15

II

3; -4

¼; 16

36

III

-3; 6

4; 2

4,5

IV

2; -5

0,04; 125

3

VI. Компьютерная презентация «Логарифмическая спираль». (5 мин)

Логарифмы вокруг нас?

VII. Рефлексия. (3 мин)

Подводим итоги. Каждый ученик считает свои баллы в индивидуальной карточке самоконтроля и видит свой результат работы на уроке. Выясняем: что получилось, а что нет, к каким моментам надо будет вернуться. Учитель собирает тетради и индивидуальные карточки самоконтроля, по которым выставляет оценки за урок.

VIII. Домашнее задание. (2 мин)

Из сборников для подготовки к ЕГЭ выбрать и решить 7 заданий, связанных с логарифмами.