Конспект урока по Алгебре "Многочлены"
Наименование ОУ: МБОУ СОШ №12 г. Саров
ФИО автора: Градова Юлия Геннадьевна
Должность: учитель математики
Конспект урока обобщения и систематизации знаний учащихся с деловой игрой «Заседание ученого совета НИИ по проблемам математики».
Тема: «Многочлены».
Цели:
Систематизировать материал по данной теме.
Провести диагностику усвоения системы знаний и умений и её применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.
Развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность.
Выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно её оценивать.
Методы: репродуктивный, частично-поисковый.
Оборудование: оценочный лист, карточки с названиями лабораторий, бочонки с номерами (от 1 до 20), карточки с заданиями.
План урока:
Мотивационная беседа.(2 мин)
Актуализация опорных знаний. (10 мин)
Игровые действия.(30 мин)
Итог урока.(2 мин)
Рефлексия.(1 мин)
Ход урока.
I. Мотивационная беседа.
Учитель: Представим себе, что сегодня наш класс – научно-исследовательский институт. А вы, ученики, - сотрудники этого института. А именно, сотрудники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании учёного совета этого НИИ, чтобы обсудить с вами тему «Многочлены». В процессе работы в НИИ вы должны: закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятных ранее моментах, проконтролировать и оценить свои знания. У каждого из вас на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце оцените свою работу как сотрудники наших лабораторий.
Оценочный лист.
Лаборатория теоретиков
Лаборатория стихотворная
Лаборатория
исследований
Лаборатория
тайн
Лаборатория
уравнений
Активность
на уроке
Всего баллов
Оценка
Девизом нашего заседания является лозунг: «Дорогу осилит идущий, а математику мыслящий». А сейчас открыли тетради и записали тему урока.
II. Актуализация опорных знаний.
Но прежде, чем войти в лаборатории НИИ, необходимо пройти испытание, которое будет пропуском в эти лаборатории. Здесь предлагается игра «Допуск», с помощью которой учитель проводит актуализацию опорных знаний.
Правила игры: На доске представлен ряд устных упражнений. В руках у учителя мешочек с бочонками, на которых указан номер упражнения. Каждый из учащихся вынимает бочонок и выполняет упражнение с указанным на нем номером.
Устные упражнения:
Упростите:
-
№1. a5·a8·a;
№6. (c5)4·c2;
№11.8a+(-3a+5a);
№16. 4yх²·(-2y);
№2. (-2x²)³;
№7. (2a2b)(ab5);
№12. 6у4+2у3;
№17.(7ab2c3)2;
№3. -4а2-3а2;
№8. 8x5y2-10х2y;
№13.(a+2)(a+3);
№18.7ab(2a+3b);
№4. a24: a12;
№9. (8x4)2 ;
№14. a4·a²;
№19. -5a·(-4a²);
№5. (-3ab)3;
№10.(2a)8: (2a2)3;
№15. (4-y)(4+y);
№20. (c4b³)4.
Итак, мы получили пропуск в лаборатории. Перед нами лаборатория теоретиков.
III.Игровые действия.
Лаборатория теоретиков.
Учащимся предлагается дидактическая игра «Математическое домино».
Правила игры: У каждого учащегося имеется карточка-домино. Карточка содержит вопрос и ответ. Первым начинает ученик, у которого карточка содержит слова «Старт» и «Финиш». Он задаёт стартовый ответ. Он же даёт финишный ответ. Каждый ученик должен внимательно следить за ходом игры, чтобы не пропустить свой ответ. Ответив, ученик задаёт свой вопрос и т.д. Учитель указывает на ошибку, если прозвучал неправильный ответ. Все учащиеся одновременно следят и за тем, чтобы был дан правильный ответ. За игру в домино в оценочный лист учащиеся ставят один балл, если верно ответили на вопрос, и 0 баллов, если пропустили свой ответ.
Карточки-домино:
Финиш: Ответ: Знаки членов, заключаемых в скобки, меняют на противоположные.
Старт: Вопрос: Что называют многочленом?
Ответ: Сумму одночленов.
Вопрос: Что называют одночленом?
Ответ: Произведение чисел, переменных и их степеней.
Вопрос: Какие слагаемые называют подобными?
Ответ: Слагаемые с одинаковой буквенной частью.
Вопрос: Как привести подобные слагаемые?
Ответ: Сложить их числовые коэффициенты, а результат умножить на общую буквенную часть.
Вопрос: Как умножить одночлен на многочлен?
Ответ: Одночлен умножить на каждый член многочлена, а результаты сложить.
Вопрос: Как перемножить одночлены?
Ответ: Перемножить числовые коэффициенты, а затем перемножить степени с одинаковыми основаниями и результаты перемножить.
Вопрос: Как умножить две степени с одинаковыми основаниями?
Ответ: Основание оставить тем же, а показатели степеней сложить.
Вопрос: Как возвести степень в степень?
Ответ: Основание оставить тем же, а показатели степеней перемножить.
Вопрос: Как умножить многочлен на многочлен?
Ответ: Каждый член одного многочлена умножить на каждый член другого многочлена и результаты сложить.
Вопрос: Как называется многочлен, состоящий из трех одночленов?
Ответ: Трехчленом.
Вопрос: Что называется степенью многочлена стандартного вида?
Ответ: Наибольшая из степеней входящих в него одночленов.
Вопрос: Что называется разложением многочлена на множители?
Ответ: Представление многочлена в виде произведения двух или нескольких многочленов.
Вопрос: По какому правилу раскрываются скобки, перед которыми стоит знак «плюс»?
Ответ: Члены, которые заключены в скобки, записывают с теми же знаками.
Вопрос: По какому правилу раскрываются скобки, перед которыми стоит знак «минус»?
Следующая Лаборатория стихотворная.
Для выполнения заданий в этой лаборатории учащимся необходимо приложить всю свою фантазию, смекалку и творчество.
1 задание: Сформулировать правило раскрытия скобок в стихотворной форме.
Пример:
Перед скобкой вижу «плюс», ошибиться не боюсь.
Знаки все я оставляю, значит, правило я знаю!
«Минус» повстречается, будьте осторожны,
Скобки раскрывайте, знаки заменяйте на противоположные!
2 задание: Выполнить задания, сформулированные в стихотворной форме.
Игра с действиями.
Я многочлен от слова «много»
Во мне всегда звучит тревога:
Как одночлены все собрать,
В какую сумму записать?
Живу всегда с друзьями в мире,
Люблю играть в примеры с ними,
А знаки «плюс», «отнять», «умножить»
Всегда играть готовы тоже.
Так вот, мой друг, сейчас давай-ка
В игру вот эту поиграй-ка.
Даю тебе два выраженья
Ты результат найди сложенья,
Затем я знаки поменяю
И все примеры прорешаем.
Даны два выражения, которые нужно сложить, вычесть из первого выражения второе, умножить.
а) (8+3х) и (2у-1);
б) (m2-2n) и (m2+3n).
В оценочный лист учащиеся ставят 5 баллов, если выполняют все задания, одно – 3 балла, ни одного – 0 баллов.
Лаборатория исследований.
Владение математикой – это умение решать задачи, причём не только стандартные, но и требующие оригинальности, изобретательности, смекалки, находчивости. В этой лаборатории учащимся предлагается дидактическая игра «Верно – неверно».
Правила игры: У каждого учащегося карточка, на которой написаны 6 равенств, среди которых есть верные, а есть и неверные. Им необходимо найти ошибки. Напротив каждого равенства нужно написать верное или неверное. Назвать ошибки.
Карточка с заданием.
(4y-3х)(4у+3х)=8у2-9х2
(0,1ху3)2=0,01х2у6
(a-b)(a+b)=a2-b2+2ab
18x2-(10x-5+18x2)= 5+10x
(3a2)3=27а5
4c4-6x2c2+8c=2c(2c2-3x2+4)
В оценочный лист 3 балла - за все правильные ответы, 2 балла - за 4 или 5 правильных ответа, 1 балл – за 3 правильных ответа.
Лаборатория раскрытия тайн.
Учитель: Межпланетная станция, запущенная для изучения планеты Марс, произвела фотосъёмку её поверхности. Побывала на ней, взяла пробу грунта и вернулась на Землю. Вместе с пробами учёные обнаружили кусок твёрдого сплава с таинственными обозначениями. Так вот эти учёные обратились к вам за помощью, чтобы вы объяснили, что обозначают эти таинственные знаки.
Задание: Найти неизвестный математический объект, заполнив пропуски.
Вариант 1.
Вариант 2.
1)3a2 · (* -2a)= 15a4-6a3;
1)2a3 · (*-7a)=8a5-14a4;
2)(10m2 - *) (*+ 10m2)= * - 4t6;
2) ( * -3b³)(*+3b³)= a2 - *;
3)* · ( x² -xy) = x²y²-xy³.
3) * · (a² - 2b)=3a³b - 6ab².
В оценочный лист 3 балла, 2 балла, 1 балл.
Лаборатория уравнений.
Учитель: Перед нами лаборатория уравнений. Давайте примем участие в исследованиях этой лаборатории. Выдающийся физик Альберт Эйнштейн – основоположник теории относительности - говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». Вот и займёмся уравнениями. На доске записаны 8 уравнений. Каждый из вас будет решать 2 уравнения. Затем нужно будет подойти к доске, отыскать полученный результат и прикрепить его обратной стороной (буквой) к своему уравнению. Если вашего результата нет, значит, уравнение решено неверно.
Уравнения:
(6y+2)(5-y)=47-(2y-3)(3y-1) 2 - А
(4-2x)+(5x-3)=(x-2)-(x+3) -2 - Л -
5-3y-(4-2y)=y-8-(y-1) 8 - Д
a·(8-9a)+40=(6-3a)(6+3a) -0,5 - Ж
16y·(2-y)+16y2-40y+25=0
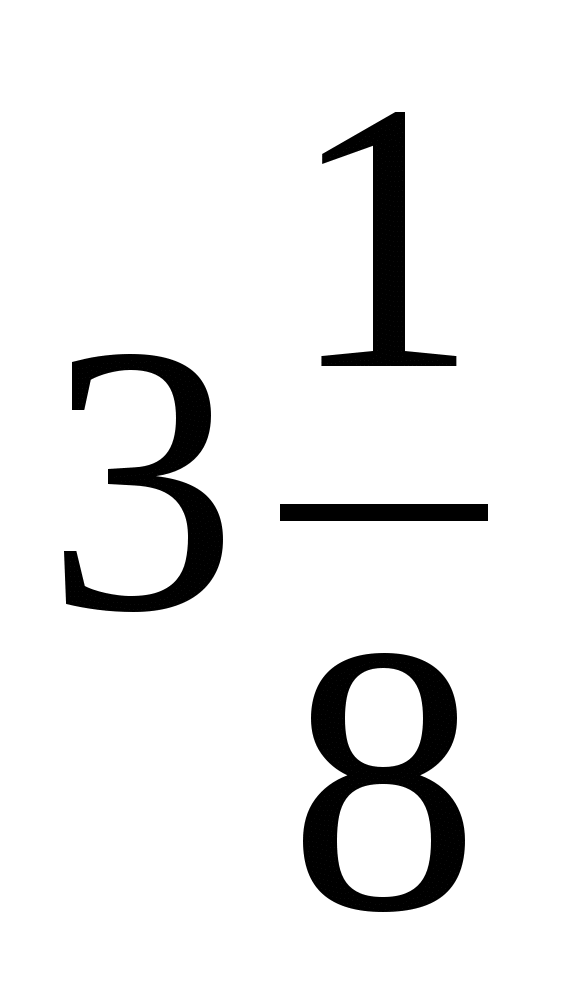 - А
- А4x(3x-1)-2x(6x+8)=5
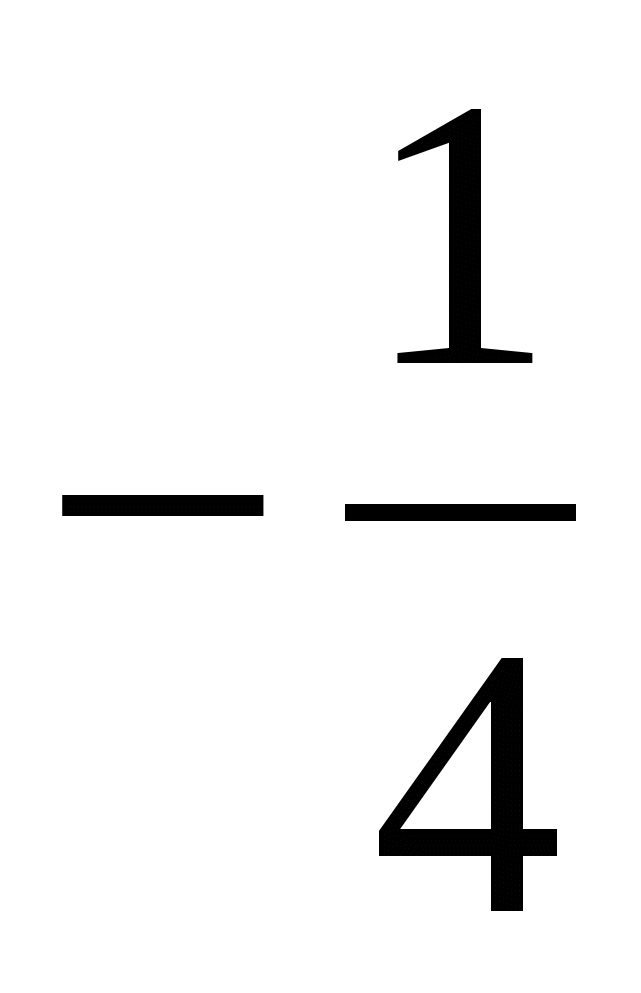 - Б
- Б4-4x+х²-х·(х+1,5)=4 0 - Р
(2х-3)(2х+3)-8х=7+4х² -2 - А
Учитель: Какими приёмами мы пользовались при решении уравнений? Мы получили загадочное слово АЛ-ДЖАБРА. Что же это за слово?
Сообщение учащегося:
Занимаясь математикой, вы не могли не заметить, что она состоит из нескольких частей. Вы научились оперировать с натуральными и дробными числами, знаете положительные и отрицательные числа. «Число» - по-гречески звучит арифмос. Поэтому наука о числе получила греческое название арифметика. Другой раздел математики посвящён различным фигурам и их свойствам и называется «Геометрия». Гео – по-гречески земля, метрио – мерею. Но вот слово алгебра – раздел математики, где решаются уравнения, рассматриваются преобразования выражений, составленные из чисел и букв – не греческое. В чём тут дело? Разве у греков не было алгебры. Была. Но решали древние греки алгебраические задачи геометрически.
А вот слово алгебра произошло от слова ал-джабра, взятого из названия книги узбекского математика, астронома и географа Мухамеда Ал-Хорезми «Краткая книга об исчислениях ал-джабры и ва-л-мукабалы». Арабское слово аль-джебр переводчик не стал переводить, а записал его латинскими буквами algebr. Так возникло название науки, которую мы изучаем. «Ал-джабра» -операция переноса отрицательных членов из одной части уравнения в другую, но уже с положительным знаком. По-русски это слово означает «восполнение».
Лаборатория Эрудитов.
Учащимся предлагается следующее задание:
С помощью рисунка разъясните геометрический смысл формулы a(b+c)=ab+ac для положительных значений a, b и c.
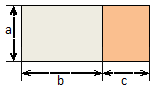
VI Итог урока.
Учитель: Каждый ученик сегодня принимал участие в необычном уроке. Сегодня, выполняя разнообразные задания, вы иногда допускали ошибки. И это неудивительно, любой человек не застрахован от ошибок, особенно, когда он только учится овладевать какой-либо наукой. Важно вовремя найти и исправить эти ошибки, понять, почему они появились, и стараться впредь не допускать их. Все, наверное, помнят поговорку: «Повторение – мать учения». Математика – не исключение, и чтобы хорошо усваивать ее, надо постоянно повторять изученное. Давайте, оценим свою активность на уроке (1-3 балла) и поставим себе оценку за урок: 14-15 баллов –«5», 10-13 баллов -«4», 7-9 баллов -«3» .
V. Рефлексия.
-Что понравилось на уроке?
-Что не понравилось?
-Что необходимо изменить, чтобы было ещё интереснее?

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ