Конспект урока по алгебре "Способы решения тригонометрических уравнений" 10 класс
МОУ «СОШ имени А.П.Чехова»
Урок алгебры в 10 классе
Тема урока:
«Способы решения тригонометрических уравнений»
Учитель математики
МОУ СОШ имени А.П.Чехова Истринского муниципального района Московской области
Мамаева Елена Васильевна
2014 год
План урока
ТЕМА:
«Способы решения тригонометрических уравнений»
Цели урока:
Образовательная:
Рассмотреть решение однородных тригонометрических уравнений и уравнений приводимых к ним
Развивающая:
развитие творческих способностей, познавательной активности;
Воспитательная:
воспитывать интерес к предмету «математика»
Тип урока: урок изучения и первичного закрепления новых знаний.
Задачи урока:
Рассмотреть решение однородных тригонометрических уравнений разных видов
Проверить овладение учащимися способами решения тригонометрических уравнений.
ХОД УРОКА.
Организационный момент
Объяснение нового материала
Уравнения в которых каждое слагаемое имеет одну и ту же степень, называется однородным
a sin f(x) + b cos f (x) = 0, а≠0, b≠0
a sin2 f (x) + b sin f (x)cos f (x)+ c cos2 f(x) =0, a≠0, b≠0, с ≠ 0
Его можно решать делением на старшую степень синуса или косинуса. При этом мы не теряем корней, т.к. если мы в данное уравнение подставим cos x =0, то получим, что sin x =0, что не возможно. sin2 x+cos2x=1
Рассматривается решение уравнений вида
a sin f(x) + b cos f (x) = 0, а и b отличны от нуля
№171 (в) учебник
Sin x+ 3 cosx=0
Раздели каждое слагаемое на cosx, получим
tgx= -3
x= 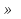 z
z
Рассматривается решение уравнений вида
a sin2 f (x) + b sin f (x)cos f (x)+ c cos2 f(x) =0, a, b, с отличны от нуля
№ 169 ( a, г)
3 sin2x + sinxcosx = 2cos2x
Разделим каждое слагаемое на cos2x, получим
3 tg2x+tgx-2=0
Ответ: x= arctg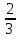 +
+  k, x=
k, x= 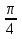 +
+ 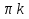
Рассматривается решение уравнений вида
a sin2 f (x) + b sin f (x)cos f (x)+ c cos2 f(x) +d =0,
a≠0, b≠0, с ≠ 0
Заменим d на d(cos2x+sin2x) и получим однородное уравнение
решить уравнение:
cos2x+3sin2x+23 sinxcosx=1
Ответ: x=πn, x= - 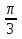 + πk
+ πk
* Решить уравнение
№ 170 (г)
* Решить уравнение
Sin (x+ 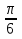 ) + cos (x+
) + cos (x+ 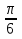 )=0,
)=0,
Ответ: - 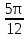 + πk, k
+ πk, k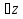
Итоги урока
Домашнее задание
№ 169 (б, в)
5sin2x + 3sincos- 2cos2=3
sin3x +cos3x=0
Повторить формулы тригонометрии
Литература:
Колмогоров А.Н. Алгебра и начала анализа: Учеб. Для 10 – 11 кл. М.: Просвещение, 2010.
Математика в школе № 10 2011г.
Т.Л.Афанасьева «Алгебра 10 класс» издание 2 Волгоград

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ