Применение скалярного произведения векторовна уроках алгебры























Применение скалярного произведения векторов
на уроках алгебры.
Учитель математики лицея №344
г. Санкт-Петербург, Воробей И.М.
Основная цель : ознакомить с данным методом и показать его эффективность при решении уравнений , систем уравнений и некоторых других алгебраических задач.
Векторный метод может быть успешно применен не только в геометрии , но и в алгебре.
Сначала напомним определение и свойства скалярного произведения векторов.
Скалярным произведением двух ненулевых векторов называется произведение их длин на косинус угла между ними :
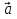
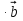 =|
=|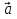 |
| |
|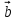 |
|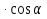 , где α – угол между векторами
, где α – угол между векторами 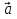 и
и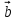
Так как |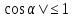 , то |
, то |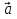 |
| |
|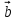 |
|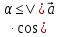 |
| |
|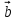 | , следовательно ,
| , следовательно ,
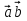 ≤|
≤|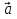 |
| |
|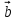 | .
| .
Если векторы 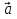 и
и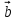 коллинеарные , то
коллинеарные , то 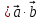 |= |
|= |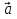 |
| |. В случаи , когда
|. В случаи , когда
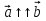 ,
, 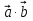 = |
= |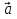 |
| |.
|.
Если векторы имеют известные в прямоугольной системе координат координаты , т.е. 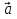 {
{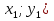 и
и 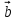 {
{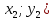 , то их скалярное произведение равно сумме произведений соответствующих координат :
, то их скалярное произведение равно сумме произведений соответствующих координат :
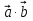 =
= 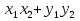 , |
, |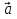 |=
|=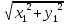 ; |
; |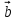 |=
|=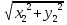 .
.
Значит, 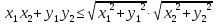 .
.
В пространстве справедливы аналогичные формулы
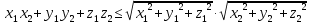 .
.
Наличие радикалов позволяет предположить , что некоторые математические задачи , например , иррациональные уравнения можно решать с помощью скалярного произведения векторов.
Рассмотрим несколько примеров. Покажем эффективность векторного метода при решении уравнений , систем уравнений и при нахождении наименьшего ( наибольшего ) значения функции.
Пример 1. Решить уравнение 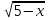 +
+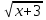 = 4.
= 4.
Решение . ОДЗ: 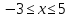 . Далее , обычно , возводят обе части уравнения в квадрат. В этом уравнении эту операцию пришлось бы произвести два раза. Можно решить это уравнение методом оценок. Покажем еще один способ , с помощью скалярного произведения векторов.
. Далее , обычно , возводят обе части уравнения в квадрат. В этом уравнении эту операцию пришлось бы произвести два раза. Можно решить это уравнение методом оценок. Покажем еще один способ , с помощью скалярного произведения векторов.
Рассмотрим вектор 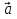 {
{ 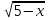 ;
;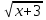 } и вектор
} и вектор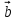 { 1 ; 1 } .
{ 1 ; 1 } .
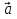
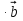 =
= 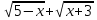 ; |
; |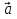 |=
|=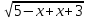 =
=  ; |
; |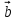 |=
|= 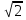 .
.
Т.к. 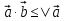 |
| |,то
|,то 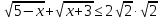 .
.
Итак , 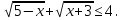 По условию
По условию 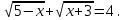
Но 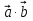 = |
= |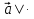 |
|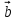 | , если векторы
| , если векторы 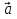 и
и 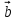 сонаправленные , т.е.
сонаправленные , т.е.
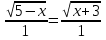 . Откуда
. Откуда 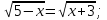
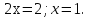
Ответ : 1.
Пример 2. Решить уравнение 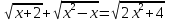 .
.
Решение. ОДЗ: 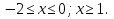 Пусть
Пусть 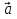 {
{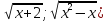 и
и 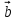 { 1; 1}.
{ 1; 1}.
|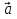 | =
| = 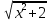 ; |
; |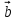 | =
| = 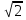 ;
; 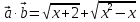 ;
;
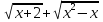
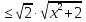 ;
; 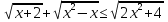 .
.
Равенство возможно только , если векторы 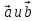 сонаправленные ,т.е.
сонаправленные ,т.е.
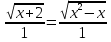 ;
; 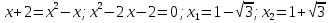 .
.
Оба корня удовлетворяют ОДЗ.
Ответ: 1 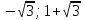 .
.
Пример 3. Решить систему уравнений 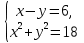 .
.
Решение . Пусть 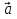 {
{ 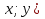 , а
, а  ;|
;|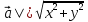 ;
; 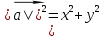 .
.
По условию 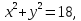 следовательно , |
следовательно , |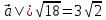 ; |
; |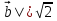 .
.
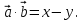 Т.к
Т.к 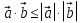 , то
, то 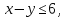 а по условию
а по условию 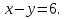
Значит, векторы 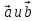 сонаправленные . Имеем
сонаправленные . Имеем 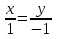 ;
; 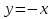 . Из 1-ого уравнения получаем
. Из 1-ого уравнения получаем 
Ответ: 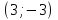
Пример 4. Решить систему уравнений 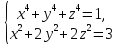 .
.
Решение . Рассмотрим вектор 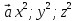 и вектор
и вектор 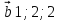 ;
;
|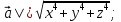 из условия имеем |
из условия имеем | |
|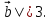
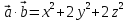 ; |
; |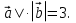 Следовательно, исходя из условия, имеем
Следовательно, исходя из условия, имеем 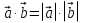 . Это равенство возможно , если векторы
. Это равенство возможно , если векторы 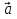 и
и 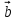 сонаправленные ,т.е.
сонаправленные ,т.е. 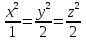 ;
; 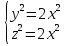 . Подставляя во 2-ое уравнение системы получим
. Подставляя во 2-ое уравнение системы получим 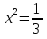 . Тогда
. Тогда 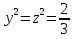 . Исходная система имеет восемь решений.
. Исходная система имеет восемь решений.
Ответ : (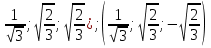 ;
; 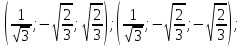
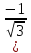 ;
;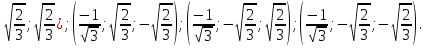
Пример 5. Доказать , что система уравнений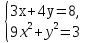 не имеет решений.
не имеет решений.
Доказательство. Пусть 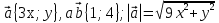 , |
, |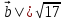 . По условию
. По условию 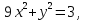 значит , |
значит , |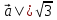 . Т.к.
. Т.к. 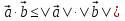 , то
, то 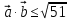 Из условия
Из условия 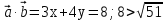 . Значит , система не имеет решений , что и требовалось доказать.
. Значит , система не имеет решений , что и требовалось доказать.
Пример 6 . При каком значении 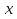 функция
функция 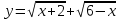 принимает наибольшее значение ?
принимает наибольшее значение ?
Решение . D(y) = [ - 2 ; 6 ] . Рассмотрим векторы 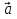 {
{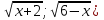 и
и 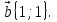
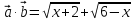 ; |
; |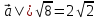 ; |
; |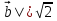 ; |
; |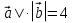 .
.
Т.к. 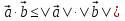 , то
, то 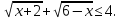 Итак , наибольшее возможное значение функции равно 4. Равенство достигается , если
Итак , наибольшее возможное значение функции равно 4. Равенство достигается , если 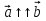 .
.
Т.е. 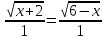 . Решив это уравнение , получим , что
. Решив это уравнение , получим , что 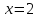 - корень уравнения.
- корень уравнения.
Ответ : при 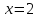 функция принимает наибольшее значение.
функция принимает наибольшее значение.
Пример 7 . Найти наибольшее значение выражения 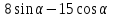 .
.
Решение . Рассмотрим векторы 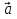 {
{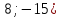 и
и 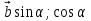 .
.
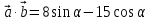 ;
; 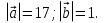 Т.к.
Т.к. 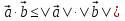 , то получаем
, то получаем 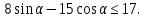 Итак , наибольшее значение выражения
Итак , наибольшее значение выражения 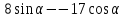 равно 17 .
равно 17 .
Ответ : 17 .
Пример 8 . При всех значениях параметра 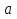 решить уравнение
решить уравнение
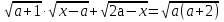 .
.
Решение . ОДЗ ( для параметра 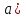 :
: 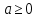 .
.
Рассмотрим векторы 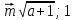 и
и 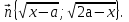
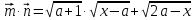 ; |
; |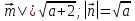 .
.
Т.к. 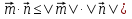 , то
, то 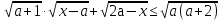 .
.
Равенство возможно , если 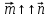 ,т.е.
,т.е. 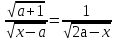 (*) . При
(*) . При 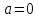 исходное уравнение имеет единственный корень
исходное уравнение имеет единственный корень 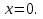
Решая уравнение (*) , получим 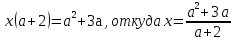 .
.
Ответ: при 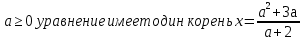 ;
;
при 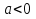 уравнение решений не имеет.
уравнение решений не имеет.
Пример 9 . При каких значениях параметра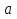 уравнение
уравнение 
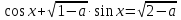 имеет решение. Найти его .
имеет решение. Найти его .
Решение . ОДЗ ( для параметра ) : 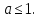
Рассмотрим 
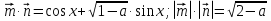 ;
;
Т.к. 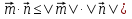 , то
, то 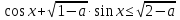 . Равенство возможно , если векторы сонаправлены , т.е.
. Равенство возможно , если векторы сонаправлены , т.е. 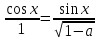 .
.
Если 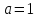 , то уравнение примет вид
, то уравнение примет вид 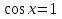 , откуда
, откуда 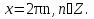
Если 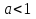 , то из пропорции получим
, то из пропорции получим 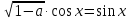 ;
; 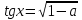 ,
,
откуда 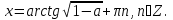
Ответ: 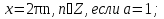
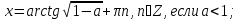
уравнение не имеет решений , если 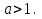
Пример 10 . Доказать неравенство 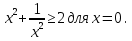
Доказательство . Докажем это неравенство с помощью скалярного произведения векторов. Рассмотрим два вектора 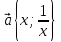 и
и 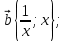
 .
.
Т.к. 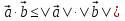 , то
, то 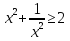 , что и требовалось доказать .
, что и требовалось доказать .
Пример 11 . Доказать , что если 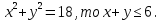
Доказательство . Рассмотрим векторы 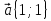 и
и 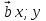 ;
; 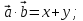
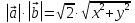 . Т.к
. Т.к 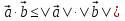 и по условию
и по условию 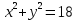 , то получим
, то получим 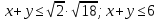 . Что и требовалось доказать .
. Что и требовалось доказать .
Было рассмотрено несколько математических задач , которые решены «векторным» методом , точнее с помощью скалярного произведения векторов. Главная трудность в использовании этого метода в решении задач заключается в выборе векторов. Нужно выбрать координаты векторов 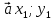 и
и 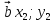 так , чтобы уравнение приняло вид
так , чтобы уравнение приняло вид  .
.

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ