Проект

«Технология проблемного обучения в преподавании математики»

Выполнил:

Базуева Вера Дмитриевна,

учитель математики

МОУ «Стрелецкая средняя

Общеобразовательная школа

Белгородского района

Белгородской области»

Белгород

2014

СОДЕРЖАНИЕ

1. ВВЕДЕНИЕ………………………………………………………… 3

2. ТЕОРЕТИЧЕСКАЯ БАЗА ПО ДАННОЙ ТЕМЕ……………… 5

3. СУЩНОСТЬ РАБОТЫ……………………………………………. 10

4. ОСНОВНЫЕ КОМПОНЕНТЫ………………………………… 16

5. НОВИЗНА РАБОТЫ……………………………………………… 20

6. ЗАКЛЮЧЕНИЕ…………………………………………………… 24

7. БИБЛИОГРАФИЯ……………………………………………….. 25

Приложение 1 Отличие проблемного обучения от традиционного обучения …………………………………………………………….. 26

Приложение 2 Конспект урока по теме: «Решение систем линейных уравнений»………………………………………………………… 27

1. ВВЕДЕНИЕ.

«Каждый человек видит тем больше нерешённых проблем, чем обширнее круг его знаний».

С.Л.Рубинштейн

Процесс проблемного обучения школьников привлекает внимание многих педагогов и психологов, так как в проблемном обучении происходит развитие подготовительной активности ребенка.

Наиболее правильное определение сущности проблемного обучения можно дать, рассматривая его с точки зрения умственного развития. Это обучение, при котором учащиеся получают знания не в готовом виде, а путем самостоятельного исследования.

Процесс обучения – это организованное взаимодействие учителя и учеников для достижения образовательных целей. Сущность процесса обучения состоит в стимулировании и организации активной учебно-познавательной деятельности учащихся по овладению ими знаниями, развитию способностей, выработке взглядов.

Одним из негативных факторов любой деятельности является невозможность достижения поставленной цели, неполучение запланированных результатов. Причины могут быть самые разные: от нереально поставленных целей до несовпадения «желаний с возможностями». Это в полной мере относится и к процессу обучения. Набившие оскомину целевые установки на «повышение качества знаний», на «развитие мышления учащихся» и т.д. так и остаются на уровне деклараций, существенно не изменяя дел на практике. Возникает масса практических вопросов:

как обеспечить гарантированность достижения целей?

как достичь запланированных результатов обучения?

как повысить эффективность образовательного процесса?

Поиски ответов на эти вопросы привели ученых и практиков к попытке «технологизировать» учебный процесс, то есть превратить обучение, в своего рода, производственно-технологический процесс с гарантированным результатом. Именно поэтому появилось специальное направление – педагогическая технология, призванная обеспечить решение поставленных выше вопросов.

В основе педагогической технологии лежит идея полной управляемости учебным процессом, проектирования и воспроизводимости обучающего цикла.

Большое место среди педтехнологий занимают педагогические технологии на основе эффективности управления и организации учебного процесса. А среди них технологии программированного обучения, имеющие целевые ориентации на эффективное обучение на основе научно разработанной программы и обучение, учитывающее индивидуальные данные ребенка.

Любая технология обладает средствами, активизирующими и интенсифицирующими деятельность учащихся, в технологии проблемного обучения и некоторых других эти средства составляют главную идею и основу эффективности результатов.

Тема исследования: «Технология проблемного обучения математике в средней школе».

Объект исследования: технология проблемного обучения

Предмет исследования: процесс обучения математике в средней школе.

Настоящая работа ставит своей целью дать характеристику технологии проблемного обучения и рассмотреть возможность ее применения на уроках математики в средней школе.

Задачи исследования:

Путем анализа педагогической литературы охарактеризовать проблемное обучение как педагогическую технологию.

Изучить возможность реализации технологии проблемного обучения, ее элементов и методов в процессе обучения математике.

Определить эффективность применения технологии проблемного обучения математике в средней школе и сформулировать условия ее применения.

2. ТЕОРЕТИЧЕСКАЯ БАЗА ПО ДАННОЙ ТЕМЕ.

Само слово «технология» происходит от греческих techne – это значит искусство, мастерство и logos – наука, закон. Дословно « технология» - наука о мастерстве.

Эффективность проблемного обучения убедительно доказана как в работах отечественных (А. М. Матюшкин, М. И. Махмутов и др.) и зарубежных (Дж. Дьюи, Э. де Боно, В. Оконь и др.) ученых, так и непосредственно на практике при обучении различным дисциплинам в разных типах школ: начальной, средней специальной и высшей.

На принципиальное отличие проблемного обучения от традиционного (репродуктивного) указывали ученые – педагоги И.Я. Лернер, М.Н. Скаткин и др. «…Его сущность состоит в том, - подчеркивали они, - что учитель наряду с сообщением готовых знаний решения проблем, стоящих перед человечеством, раскрывает и пути их приобретения, вооружает методами науки и техники».

Главная цель обучения – не простое усвоение программного материала, а овладение определенными способами добывания знаний и отысканием ответа на вопрос: «Как вы это узнали?»

Все в сущности сводится к трем слагаемым: научить владеть «методами науки и техники»; развить познавательные способности человека; привить любовь к учебе, труду, сформировать активную жизненную позицию.

Если при репродуктивном обучении механизмом реализации учебной задачи служит учебный материал, то при проблемном – сама методика. Однако не любая методика может реализовать учебную задачу, а только такая, которая имеет двойственное значение.

С одной стороны, она (методика), как и в традиционном обучении, является средством донесения информации, а с другой, она же является учебной задачей, т.е. учебным материалом, который подлежит обязательному изучению.

Основными понятиями проблемного обучения являются понятия «проблемная ситуация», «учебная проблема», «ученическая гипотеза», «взаимодействие преподавателя и учащихся», «теория учения» и др.

Проблемное обучение возникло не эмпирически в результате обобщения передового опыта преподавателей, а с помощью дедукции, – как результат интеграции понятий смежных с педагогикой наук, в первую очередь – логики и психологии. Оно родилось на стыке гносеологии (диалектическая противоречивость развития объектов действительности), логики научного исследования (проблема как форма отражения противоречивости процесса познания действительности), психологии (возникновение состояния любопытства, эмоционально – чувственной реакции на объект и интеллектуального затруднения, вызывающего исследовательский рефлекс «почему?»), дидактики (возникновение принципов и правил организации содержания, форм и методов обучения с учетом обозначенных выше закономерностей и изменение логики взаимодействия деятельностей преподавания учения).

Проблемное обучение – это такая организация учебных знаний, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие личностных способностей.

Проблемное обучение основывается на творческих положениях американского философа, психолога и педагога Дж. Дьюи, который считал, что ребенок повторяет в своем познании путь человечества. Он усваивает материал, не просто слушая или воспринимая органами чувств, а как результат удовлетворения возникшей у него потребности в знаниях.

Условиями успешности обучения являются:

- проблематизация учебного материала «знания – дети удивления и любопытства»;

- активность ребенка;

- связь обучения с жизнью ребенка, игрой, трудом;

Проблемное обучение основано на создании особого вида мотивации – проблемной, потому требует адекватного конструирования дидактического содержания материала, который должен быть представлен как цепь проблемных ситуаций, причем оптимальной структурой материала будет являться сочетание традиционного изложения с включением проблемных ситуаций.

Как показывает практика, проблемные ситуации могут быть разными по уровню проблемности, содержанию, виду рассогласования информации.

В практике работы учителя математики могут быть использованы разнообразные проблемные ситуации.

Не могу!

Дается практическое задание не выполняемое вообще

Несоответствие

Дается задание, где надо использовать знания в новой ситуации

Конфликт

Ситуация рассматривающая противоположности

Неожиданность

Вызывает удивление, необычностью, парадоксальностью

Неопределенность

Неоднозначные решения в виду недостатка данных

Выбор

Дается ряд готовых решений. Выберите правильное

Ошибка

Задания с заведомо допущенной ошибкой

Методические приемы создания проблемных ситуаций:

- учитель подводит школьников к противоречию и предлагает им самим найти способ его разрешения;

- сталкивает противоречия в практической деятельности;

- излагает различные точки зрения на один и тот же вопрос;

- предлагает классу рассмотреть явление с различных позиций (например, с точки зрения юриста, финансиста, педагога);

- побуждает обучаемых делать сравнения, обобщения, выводы из ситуации, сопоставлять факты;

- ставить конкретные вопросы (на обобщение, обоснование, конкретизацию, логику рассуждения);

- определяет проблемные теоретические и практические задания (например, исследовательские);

- ставит проблемные задачи (например, с недостаточным или избыточными исходными данными, с неопределенностью в постановке вопроса, с противоречивыми данными, с заведомо допущенными ошибками, с ограниченными временами решения, на преодоление «психологической инерции» и др.).

Для реализации проблемной технологии необходимы:

- отбор самых актуальных, сущностных задач;

- определение особенностей проблемного обучения в различных видах учебной работы;

- построение оптимальной системы проблемного обучения. Создание учебных и методических пособий и руководств;

- личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка.

Вариантами проблемного обучения являются поисковые и исследовательские методы, при которых учащиеся ведут самостоятельный поиск и исследование проблем, творчески применяют и добывают знания.

В зависимости от характера действий по разрешению породивших ее противоречий учебного познания можно говорить о разных уровнях проблемности.

Первый уровень определяется наличием в учебном материале объективного противоречия и его выражением в форме проблемы: учитель создает проблемную ситуацию и показывает все этапы выхода из нее. Второй уровень связан с процессом коллективного поиска способов решения проблемы: в возникшей проблемной ситуации учащиеся вместе с учителем выдвигают и обосновывают различные гипотезы. Третий уровень: осознав содержание поставленной проблемы, учащиеся сами выдвигают и обосновывают гипотезу и вместе с учителем доказывают ее. Четвертый уровень: учащиеся сами ставят проблему (или принимают формулировку учителя), самостоятельно выдвигают и обосновывают гипотезу, доказывают ее и проверяют правильность решения проблемы.

Уровни проблемности определяются природой проблемной ситуации и закономерностями познавательного процесса: одни учащиеся принимают проблему, другие - нет, одни умеют обосновывать гипотезу и доказывать ее, другие не умеют и т.д.

Разные уровни проблемности выступают объективной основой построения различных вариантов сочетания приемов преподавания и приемов учения, т.е. различных дидактических конструкций, в частности, различных методов обучения.

Современная действительность требует выпускников, умеющих творчески мыслить, самостоятельно приобретать знания, владеть методологией и способами учебно-познавательной деятельности, умениями генерировать новые идеи.

Чтобы выпускник был конкурентоспособным необходимо, развивать ключевые компетенции, такие как
– готовность и способность обучаться самостоятельно;
– уверенность в себе;
– самоконтроль;
– самостоятельность мышления, оригинальность;
– критическое мышление;
– готовность использовать новые идеи и инновации для достижения цели;
– способность общаться;
– способность принимать решения;
– способность к совместной работе ради достижения цели;
– способность слушать других людей и принимать во внимание то, что они говорят;
– способность самостоятельного применения, построения алгоритма и его анализ.

Проанализировав современные требования к выпускникам, задаешься вопросом, каким образом можно достичь желаемых результатов.

Очевидно, что стимулом для познавательной активности учащихся становится познавательная потребность, зависящая в первую очередь, от значимости информации, которая может быть получена в результате решения проблемы, а также интереса, который вызывает у учащегося изучаемая тема.

Технология проблемного обучения базируется на единстве принципов системного квантования и проблемности. Технология включает в себя целевую компоненту, ведущие принципы, специальные способы проектирования содержания обучения, систему задач и упражнений, конструирование дидактических материалов, рейтинговую систему контроля и оценки учебных достижений.

3. СУЩНОСТЬ РАБОТЫ.

В настоящее время под проблемным обучением понимают такую организацию учебного процесса, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению.

Технология использования элементов проблемного обучения в моей работе – это комплексная поддержка и помощь учащимся в решении задач развития, обучения и воспитания.

Цель применения технологии проблемного обучения: научить учащихся идти путем самостоятельных находок и открытий.

Главная ценность использования проблемных ситуаций состоит в том, что дети в очередной раз получают возможность сравнивать, наблюдать, делать выводы; убеждаются в том, что не на каждый вопрос есть готовый ответ, что ответ может быть неоднозначным, что каждый из них имеет полное право искать и находить свой ответ, отстаивать свое мнение. Изменения, происходящие в детях, указывают на то, что учебные проблемы создают благоприятные условия для общего развития каждого ребёнка. Разрешение системы проблемных ситуаций приучает школьников к умственному напряжению, без чего невозможна подготовка к жизни, к труду на пользу общества.

Многие педагоги видят суть проблемного обучения в противоречии между знаниями и отсутствием необходимых знаний. Но тогда возникает вопрос: «Каков путь от незнания к знанию?».  Если он лежит через заучивание, то здесь и проблемы нет. Но если для усвоения нового материала необходимы самостоятельные поиски, связанные с исследованием предметов и явлений, с выявлением их связей, изменений, то есть возникает проблемная ситуация, то здесь требуется напряжение умственной деятельности.

Выделим три группы проблемных ситуаций:

1. Познавательные (теоретическое мышление);
2. Оценочные  (критическое мышление);
3. Организаторско - производственные  (практическое мышление).

Познавательные проблемы решаются сравнением, выдвижением гипотез, предположений и т.д. В результате появляются новые законы и выводы в науке, новые понятия…

Оценочные проблемы требуют критической оценки предметов и результатов труда.

Решение организаторско - производственных проблем связано с поиском путей различных положительных изменений окружающей действительности и способствует развитию практического мышления, а также ведёт к поиску применения знаний на практике.

Рассмотрим подробнее некоторые ситуации.

1. Познавательные проблемы.

1.1 На каждом уроке возможно привлекать учащихся к самостоятельному определению понятий. На основании наблюдений, описаний ученики выделяют существенные признаки предмета или явления. Например, учащиеся усвоили понятие «прямоугольник» и переходят к изучению квадрата. Необходимо определить понятие «квадрат». На доске я рисую несколько  квадратов разных по размерам,  положению, по цвету. Нужно установить, что общего во всех этих фигурах, дать определение понятия «квадрат». После многократного повторения этот приём закрепляется в сознании школьника как способ определения понятия, как средство познания окружающей действительности. Можно выделить два этапа формирования понятий:

- Постановка вопросов для изучения фактов, всесторонний анализ явления.
- Выделение существенных признаков предметов и явлений  (учитель составляет вопросы, которые помогают раскрыть суть явления, проводит беседу, в результате которой формируются новые понятия).

1.2 Главное в решении познавательной проблемы – привлечь школьников к решению данной проблемы, заинтересовать их новой деятельностью.

1.3 Сравнение.   Иногда сравнение выступает как самостоятельная проблема: сравни геометрические фигуры и т. д. Сравнение помогает глубже понять предметы и явления.

С помощью сравнения устанавливается  сходство и различие предметов и явлений по определенным признакам.

1.4 Наиболее сложная познавательная проблема, которую решают ученики на уроке, это выдвижение обоснованных гипотез. На основании имеющихся сведений  ученики должны сделать обоснованные предположения. В процессе выдвижения гипотез важно научить школьников обосновывать предположения, обращать внимание на существенность, достаточность аргументов, из которых вытекает предположение. Чем твёрже, глубже обосновано предположение, тем ближе оно к истине.

2. Оценочные проблемы.

Оценочные проблемные ситуации позволяют развить критическое мышление учащихся. Нет такой области жизни, где бы не приходилось оценивать предметы и явления. Умение правильно, критически мыслить необходимо всем людям.

Обычно на уроке учащимся приходится опровергать ложные суждения. В процессе этой работы они должны проявить высокую наблюдательность и путём сопоставления найти ошибку.

Примеры заданий:

- равным наклонным соответствуют равные наклонные;

- если произведение двух чётных чисел чётное число, то и сумма этих чисел чётное число;

- биссектриса угла в равнобедренном треугольнике есть одновременно его высота и медиана;

- в цветочном магазине продавали 67 роз. Красных было на 4 больше, чем белых. Сколько было красных и белых роз отдельно?

Как правило,  учителя предлагают учащимся задания, в которых ошибки исключаются. В результате у школьников вырабатывается абсолютное доверие сообщениям, указаниям, заданиям. Чтобы этого избежать, необходимо развивать у школьников способность к анализу, умению находить ошибки и обосновывать их. Прививать школьникам эти навыки надо постепенно:  сначала научить определять суждение, в котором имеется ошибка, затем подбирать аргументы, опровергающие ошибки и, наконец, развёрнуто и   последовательно строить опровержение. Опровергнуть суждение – значит установить его ложность; приводимый аргумент должен точно соответствовать логическим законам, правилам. Учитель использует различные приемы для поиска ошибок: взаимопроверка, рецензирование и диспут.

3. Организаторско - производственные проблемы.

Организаторско - производственные ситуации способствуют подготовке учащихся к активной  деятельности на производстве, развивают практическое мышление, учат находить выход из возможных трудных положений. На уроках по различным предметам можно и необходимо готовить учащихся  к труду, к  выбору профессии, учить решать проблемы, которые возникают в процессе практической деятельности. Знания учащихся становятся более глубокими и прочными, обогащаются новыми фактами.

В ходе изучения научно – методической литературы и на основании опыта работы над проектом определены условия повышения эффективности проблемного обучения:

1. Учащиеся на одном уроке должны решать разного вида проблемы.

2. Перед решением проблемных заданий необходимо мотивировать полезность их выполнения.

3. Необходима систематичность в организации проблемного обучения на уроках.

4. Одна проблема должна решаться письменно, т.е. в её решении принимают участие все учащиеся.

5. Необходимо глубокое усвоение  школьниками программного материала.

6. Учёт индивидуальных особенностей учащихся в процессе выполнения проблемных заданий.

7. Постепенное усложнение проблемных заданий, постоянное включение нового, неизвестного.

Известно, что процесс обучения математике в школе включает три основные составляющие:

– объяснение нового материала;
– самостоятельная работа;
– опрос учащихся.

Практика работы над реализацией проекта показала, что объяснение нового материала является эффективным, если содержание передаваемой информации и форма её подачи обеспечивают необходимую активность учащихся,  и от того, как учитель организует объяснение, во многом зависит качество их  знаний. Нередко при изучении геометрии параграф начинается сразу с определения или формулировки теоремы, поэтому учителю самому приходится продумывать вводные замечания, связывать данную тему с предыдущей, создавать проблемные ситуации, подыскивать материал, который бы заинтересовал учащихся. Например, урок, посвящённый трапеции, можно начать сразу с определения, а можно начать так: «Приходилось ли вам слышать слово «трапеция» раньше? Знаете ли вы, что оно означает? Сегодня на уроке мы узнаем, какая фигура в геометрии называется трапецией и каковы её свойства».

А можно начать урок с изображения на доске различных выпуклых четырёхугольников. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и  новый четырёхугольник (трапеция). Учащимся предлагается назвать их и дать  определение, а неизвестный четырёхугольник назвать «трапецией»  и  попросить учащихся дать самим определение (учащиеся должны увидеть  параллельность  только двух сторон).

Несколько иначе приходится начинать урок, на котором доказывается теорема. Возьмём урок «Теорема Пифагора». Начать можно с исторических сведений, рассказать о Пифагоре, а уж затем перейти к доказательству самой теоремы. Изложение исторического материала занимает немного времени и способствует повышению интереса к изучаемой теме. И всё же наиболее целесообразным является вариант, предусматривающий создания проблемной ситуации: «Рассмотрим задачу. В прямоугольном треугольнике катеты равны 4 и 3 сантиметра. Чему равна гипотенуза этого треугольника?»  Потом продолжаем: «Пока вы не можете решить такую задачу. Это не удивительно,  так как для её решения необходимо знать очень важную теорему, с которой мы и познакомимся».

Предлагая учащимся задачу, решение которой возможно только с применением теоремы Пифагора, мы тем самым ставим проблему, как найти гипотенузу, зная катеты треугольника. Благодаря созданной проблемной ситуации, восприятие нового материала делается осознанным, целенаправленным, что способствует его глубокому усвоению.
Проблемную ситуацию можно создать, например, при построении биссектрисы угла, делении отрезка пополам и т.д.
Проблемное обучение эффективно способствует формированию у учащихся математического склада мышления, появлению интереса к предмету, прививает навыки исследовательской работы и желание самостоятельно решать возникшие ситуации.

4. ОСНОВНЫЕ КОМПОНЕНТЫ.

В результате работы над проектом выявлены наиболее эффективные способы организации начала урока:

1. Предлагается задача, которая решается  только с опорой на жизненный опыт ребят, на их смекалку.

2. Даётся задача на тренировку памяти, наблюдательности, на поиск закономерностей по материалу, хорошо известному школьникам.
3. На доске записаны уравнения и ответы к ним, среди которых есть как верные, так и неверные. Предлагается проверить их.
4. На доске записано решение какого-либо примера или задачи с традиционными, наиболее часто встречающимися ошибками. Надо осуществить проверку каждого логического хода решения, преследуется цель получить наиболее полное обоснование критических замечаний.
5. Даётся обычная традиционная задача с традиционным решением. Предлагается найти более короткое, рациональное решение.
6. На доске дан чертёж к сложной задаче и осуществляется коллективный поиск её решения.

7. На столе у каждого ученика лежит чистый лист бумаги. Объявив тему урока, учитель сообщает,  что в конце урока по некоторым рассмотренным на уроке вопросам будет проведена проверочная работа на 15 минут.
8. Урок начинается с чтения по фразам  заданного для самостоятельного изучения параграфа и коллективного обсуждения его смысла. Ученики ответами на вопросы учителя доказывают глубину изучения темы.
9. Ребята изображают некоторую геометрическую фигуру и проводят небольшую исследовательскую работу по определённому плану.
10. Обсуждаются различные способы решения задачи заданной на предыдущем уроке. Эта задача, решение которой требует исследовательской работы, должна быть необычной, интересной, но доступной для всех учащихся.
11. Если на дом было дано творческое задание, то урок надо начинать с представления наиболее удачных работ.

12. Рассматривается некоторая математическая проблема, которая ещё не обсуждалась в классе. Ученики намечают план её решения.

Структура урока с математической проблемой:

1.Организационный момент

- включение детей в деятельность;

- выделение содержательной области.

2. Актуализация знаний

- воспроизведение понятий и алгоритмов, необходимых и достаточных

для «открытия» нового знания;

- фиксирование затруднения в деятельности по известной норме.

3. Постановка учебной проблемы

- определение затруднения, его место.

- определение необходимости нового знания.

4. «Открытие» учащимися нового знания

- выдвижение гипотезы;

- проверка гипотезы.

5. Первичное закрепление

- внешнее оформление новых алгоритмов;

- фиксирование уже оформленного знания.

6. Самостоятельная работа с самопроверкой и самооценкой в классе;

- самостоятельное решение типовых заданий;

- самостоятельная проверка учащимися своей работы.

7. Повторение

- включение нового материала в систему знаний;

- решение задач на повторение и закрепление ранее изученного материала.

8. Итог занятия

- рефлексия деятельности на уроке;

- самооценка учащимися собственной деятельности

Особое значение в обучении имеет искусство ставить вопросы.

Знаменитый древнегреческий учёный Аристотель трактует вопрос как мыслительную форму, обеспечивающую переход от незнания к знанию. Любая система вопросов регулирует деятельность учеников, направляет её в необходимое русло. Чаще всего вопросы учителя подсказывают лишь область поиска решения.

Пример. Поиск решения задачи  с помощью уравнения.

- Какие процессы описаны в условии задачи?

- Какими величинами характеризуется каждый процесс?

- Что нам известно о каждой величине?

- Какую зависимость между величинами выберем для составления уравнения?

Эти вопросы организуют работу учеников на первой основной фазе решения, на этапе анализа ситуации. Вопросы направлены на поиск закономерностей между величинами.

На проблемном уроке надо создать все условия для проявления познавательной активности учеников. Учащиеся не получают готовые знания, а в результате постановки проблемной ситуации испытывают затруднение либо удивление и начинают поиск решения, открывая новые знания самостоятельно. Затем проводим обязательное проговаривание алгоритма решения и применяем его на практике при выполнении самостоятельной работы. Проблемное обучение вызывает со стороны учащихся живые споры, обсуждения, создается обстановка увлеченности, раздумий, поиска. Это плодотворно сказывается на отношении школьника к учению. Постоянная постановка перед ребенком проблемных ситуаций приводит к тому, что он не “пасует” перед проблемами, а стремится их разрешить.

Приемы создания проблемных ситуаций.

- Подведение школьников к противоречию и предложение самим найти способ его разрешения;

- Изложение различные точки зрения на один и тот же вопрос;

- Предложение классу рассмотреть явление с различных позиций;

- Побуждение учащихся делать сравнения, обобщения, выводы из ситуации, сопоставлять факты.

- Постановка конкретных вопросов на обобщение, обоснование, конкретизацию, логику, рассуждения.

- Определение проблемных теоретических и практических заданий;

- Постановка проблемных задач (например: с недостающими, избыточными или противоречивыми данными, с заведомо допущенными ошибками).

Задача учителя - находить, конструировать полезные для познавательного процесса противоречия, привлекать школьников к их обсуждению и решению, естественно, не требуя никаких специальных упражнений, искусственно подбираемых ситуаций.

Обучаясь по данной технологии, у ребят появилась уверенность в своих силах и знаниях.

5. НОВИЗНА РАБОТЫ.

Новизна работы состоит в том, что при создании определенных организационных условий для решения проблемных ситуаций, стимулируя поиск недостающих знаний для разрешения познавательного противоречия, происходит формирование познавательных учебных действий.

Наиболее эффективны следующие три способа организации проблемного обучения: проблемное изложение, поисковая (эвристическая) беседа, самостоятельная поисковая и исследовательская деятельность учащихся.

Способы организации проблемного обучения

Способ организации

Деятельность учителя

Деятельность ученика

Задачи

Проблемное изложение

Ставит проблему, выдвигает гипотезу, показывает путь ее доказательства, формирует вывод

Мысленно следит за процессом творческого поиска и логикой доказательства

Формирование образца мыслительных действий в проблемной ситуации

Частично-поисковой

Конструирует общее задание, расчленяет его на вспомогательные, намечает план поиска, консультирует

Самостоятельно осуществляет последующие этапы поиска решения по составленному плану при корректирующей роли педагога

Формирование элементарных умений и навыков поисковой деятельности

Исследовательский

Объявляет тему, постепенно подводит к необходимости протии весь путь поиска: постановка проблемы, решение выводы

Самостоятельно формулирует проблему, находит ее решение, делает выводы

Формирование навыков исследовательской, творческой деятельности

Новизна в методах обучения и воспитания состоит в том, что учитель:

- управляет познавательной деятельностью ученика, т.е. переходит с позиции носителя знаний (дающего знания) в позицию организатора собственно познавательной деятельности учащихся;

- мотивирует познавательную деятельность ученика на уроке за счет коммуникации, взаимопонимания и добивается положительного отношения к предмету;

- организует самостоятельную работу на уроке;

- создает ситуацию успеха, т.е. предлагает задания, посильные ученику;

- создает положительную эмоциональную атмосферу учебного сотрудничества, которое реализуется в системе гуманных учебных взаимоотношений.

Изучение научно-методической литературы по проблеме и опыт работы помогли составить технологическую карту реализации методики дидактических задач (см. таблицу).

Технологическая карта

Этапы занятия

Цели

Время

(мин)

Содержание деятельности

Формы и методы

1.

Постановка темы и целей

Мотивировать учащихся на активную познавательную деятельность

2

Обоснование значимости рассматриваемого материала в практической деятельности. Формулировка целей (план на доске)

Фронтальная беседа

2.

Постановка задачи

Воспринять и осмыслить задание

3

Ознакомление с дидактической задачей. Выяснение возможностей разрешения заданной ситуации

Фронтальная беседа

3. Информирование

Усвоить новую информацию

7

Работа с информационным листом

Индивидуальная работа

4. Планирование и принятие решения

Уметь рационально использовать новую информацию

3

Составление плана действий

Самостоятельная работа в группах

5. Выполнение

Знать: алгоритм решения систем уравнений способом подстановки. Уметь: решать системы двух линейных уравнений с двумя неизвестными

19

Составление алгоритма решения систем уравнений способом подстановки,

решение системы двух линейных уравнений с двумя неизвестными способом подстановки, анализ решения, решение дидактической задачи

Работа в группах. Фронтальная работа. Индивидуальная работа

6. Контроль

Проверить полноту и правильность выполнения заданий

6

Сравнение составленного алгоритма с эталоном. Выявление собственных ошибок. Анализ решения. Проверка решения дидактической задачи

Контроль учителя. Самоконтроль. Фронтальная беседа. Межгрупповая взаимопроверка

7. Оценка

Уметь оценивать деятельность в соответствии с критериями

5

Заполнение оценочного листа и обсуждение достижения поставленных целей

Самооценка. Работа в группах

Рассмотрим последовательность фаз приведённого выше занятия.

Информация. Занятие начинается с постановки дидактической задачи практического характера. Через близкую к реальной жизни постановку задания достигается двойная цель. Во-первых, учащиеся видят, с какими требованиями они могут столкнуться в реальной жизни, и, во-вторых, возникает адекватная ситуация запроса необходимых знаний и умений.

Планирование. Поскольку задание для учащихся является новым и подобрано так, что с помощью имеющихся знаний и умений его решить нельзя, то у них возникает информационный дефицит. Учащиеся запрашивают недостаточную информацию, и учитель предоставляет её в форме информационных листов. Обучающиеся изучают предложенную им информацию и направляют её для решения ранее возникшей проблемы.

Принятие решения. В этой фазе занятия планируется дальнейший ход действий для решения дидактической задачи. Число и последовательность учебных этапов определяется так же, как и средства, необходимые для каждого учебного этапа.

Выполнение. За принятием решения следует воплощение запланированного в конкретные действия. В нашем примере на этой фазе происходит групповое определение алгоритма решения систем уравнений способом подстановки, индивидуальное решение предложенных систем двух линейных уравнений с двумя неизвестными способом подстановки, групповой анализ предложенных решений систем уравнений (поиск ошибок в решении). Завершает этот этап решения дидактической задачи.

Контроль, который наступает после выполнения заданий.

Оценка. Занятие заканчивается оценкой решения дидактической задачи.

Следует заметить, что фазы “контроль” и “оценка” могут идти параллельно, причём сразу по мере выполнения промежуточных задач заполняется оценочный лист. В конце занятия осуществляется перевод полученных баллов в отметку.

Таким образом, становится очевидной возможность адаптации предметного курса математики к требованиям проблемного обучения.

Анализ и обобщение передового педагогического опыта показывают, что те или иные элементы технологии проблемного обучения находили и находят свое применение при обучении математике, демонстрируя эффективность и оказывая влияние на повышение качества учебного процесса.

6. ЗАКЛЮЧЕНИЕ.

Ознакомившись с большинством современных публикаций по теории и из собственного опыта учителя, можно сделать вывод, что на данном этапе развития человечества проблемное обучение просто необходимо. Проблемное обучение формирует гармонически развитую личность, способную логически мыслить, находить решения в различных проблемных ситуациях, способную и систематизировать и накапливать знания, способную к высокому самоанализу и саморазвитию.

Конечно, проблемный тип обучения не решает всех образовательных задач, поэтому он не может заменить собой всей системы обучения, включающей разные типы, способы и формы организации учебного процесса. Однако следует понимать, что функции проблемного обучения - это содействие эффективному усвоению учащимися системы знаний и способов умственной и практической деятельности; выработка умения творчески применять полученные знания в новой ситуации, решать учебные проблемы; воспитание познавательной самостоятельности, ведущей к приобретению опыта творческой деятельности и развитию творческих способностей детей.

VII. Библиография

1.  Бабанский Ю.К. Методы обучения в современной общеобразовательной школе.-М. Просвещение, 1985.

2.  Бабанский Ю.К. Проблемное обучение как средство повышение эффективности учения школьников.- Ростов-на-Дону, 1970.

3.  Вилькеев Д.В. Познавательная деятельность учащихся при проблемном характере обучения основам наук в школе.- Казань, 1967.

4.  Гальперин П.Я. Методы обучения и умственное развитие ребенка. - М.:Изд-во МГУ, 1985.

5.  Крутецкий В.А. Психология обучения и воспитания школьников. - М.: Просвещение, 1986.

6.  Кудрявцев Т.В. Исследование и опыт проблемного обучения. В кн.: «О проблемном обучении»: Вып. 2.- М.:Высшая школа, 1969.

7.  Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы. - М.:3нание, 1991.

8.  Лернер И.Я. Вопросы проблемного обучения на Всесоюзных педагогических чтениях.// Советская педагогика.-1968.-№ 7.

9.  Лернер И.Я. Система методов обучения. - М.: Знание, 1976.

10.  Людмилов Д.С., Дышинский Е.А., Лурье A.M. Некоторые вопросы проблемного обучения математике: Пособие для учителей.- Пермь, 1975.

11.  Матюшкин A.M. Проблемные ситуации в мышлении и обучении.- М.: Педагогика, 1972.

12.  Махмутов М.И. Организация проблемного обучения в школе. Книга для учителей.- М.: Просвещение, 1977.

13.  Махмутов М.И. Проблемное обучение. Основные вопросы теории.- М.: Педагогика, 1975.

14.  Мочалова Н.М. Методы проблемного обучения и границы их применения.- Казань, 1978.

15.  Оконь В. Основы проблемного обучения.- М.: Просвещение, 1968.

Приложение 1

Отличие проблемного обучения от традиционного обучения

Показатели сравнения

Традиционное обучение

Проблемное обучение

цели

Добывание знаний учащимися собственным трудом.

Добывание знаний с помощью учителя.

Этапы урока: этап № 1

Организация внимания учащихся

Этап № 2

Актуализация ранее изученного: учитель задаёт наводящие вопросы с целью повторения ранее пройденного материала.

Инструкция: обращение к предыдущему опыту (например, учитель напоминает, что степенную функцию учащиеся уже изучали, здесь идёт повторение свойств, построение графиков, ситуация, где она используется?

Этап № 3

Изучение нового материала: учитель сам объясняет тему, приводит примеры, а потом требует от учащихся.

Обсуждение темы в группе: класс делится на группы, сначала идёт обсуждение темы в группе, а потом со всем классом.

Этап № 4

Закрепление: учитель предоставляет учащимся определённые номера на данную тему, и учащиеся закрепляют свои знания на практике.

Разрыв – момент, когда учащиеся должны осознать, что в их знаниях имеются пробелы, которые они сами должны восполнить.

Этап № 5

Вторичное закрепление: учитель уже для закрепления новой темы даёт более сложные задания.

Рефлексия – определение степени усвоения.

Этап № 6

Подведение итогов урока

Приложение 2

КОНСПЕКТ УРОКА ПО ТЕМЕ: «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»

Предмет: математика; учебник «Алгебра 7 класс» авторы Ю.Н. Макарычев.

Дидактическая цель: организовать совместную деятельность, создающую условия для демонстрации учащимися умения формулировать гипотезы, формирования мышления, характерного для математической деятельности;

Логика урока – Учебное занятие закрепления новых знаний и способов деятельности.

Тема: «Решение систем линейных уравнений».

Цели урока:

Образовательные:

совместно с учащимися разработать способы решения систем линейных уравнений;

Развивающие:
организовать совместную деятельность, создающую условия для демонстрации учащимися умения формулировать гипотезы, формирования мышления, характерного для математической деятельности;
Воспитательные:

воспитание чувства дружбы, взаимовыручки, умения работать в команде и ответственности за результаты совместной работы.

Методы обучения: проблемная и личностно - ориентированная технология обучения.

Формы организации познавательной деятельности учащихся:

- фронтальная;

- индивидуальная;

- самостоятельная.

Средства обучения:

Для учащихся: рабочие тетради, презентация, схемы, таблицы

Для учителя: мультимедийная презентация «Решение систем линейных уравнений».

Ход урока:

1.Погружение в проблемную ситуацию.
Приветствие учащихся. Повторение ранее изученного материала: (учащиеся сами определили круг вопросов, задавали друг другу)

Что называется уравнением? (Уравнение – это равенство, содержащее одну или несколько переменных) - линейное уравнение с 1 переменной.

Что называется линейным уравнением с 2 переменными? ()

Приведите примеры линейных уравнений с 2 переменными.

Что является решение линейного уравнения с 2 переменными?

Задача 1: Разность двух чисел равна 6. Найдите эти числа. ()

Какие свойства уравнений вы знаете?

Свойства уравнений:

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

II. Создание проблемной ситуации.
Задача 2: Разность двух чисел равна 4, а их сумма равна 0.Найдите эти числа.

Чем отличаются условия 1 и 2 задачи?

Мы получили с вами 2 уравнения, они объединены одним условием. В алгебре говорят, что получили систему уравнений.

Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно

III. Работа по обоснованию версий в группах.

Сейчас поработайте в группах, рассмотрите данную систему уравнений и попробуйте предложить способы решения данной системы. (Способы решения фиксируются на доске.)

Решите систему уравнений одним из предложенных способов по желанию.
Представители каждой из команд выходят к доске и предлагают свой вариант решения системы уравнений.
Задача 3: Решите систему уравнений: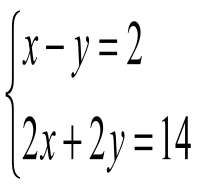
Ответ: (4;2)
Задание группам:

Решите своим методом следующую систему уравнений.

Попробуйте обосновать свой вариант решения и сформулировать правило (алгоритм) решения системы.

Как узнать правильность предложенной вами гипотезы. (Как проверить, правильно ли решена система?)

Что является решение системы линейных уравнений с 2 переменными?

Предложите название своего метода решения системы.

VI. Представление результатов работы групп.
(представители каждой команды выходят к доске и предлагают свои варианты решения системы)
Вывод: Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Итак, одна и та же система решена разными способами.

Какой из них вам показался более удобным?

В чем недостаток графического метода?

Все эти способы в математике имеют свои названия: графический, сложения, подстановка.
V. Итог урока:

способы решения систем уравнений с 2 переменными;

алгоритмы способов решения систем уравнений с 2 переменными;

проверка решения.

VI. Оценивание работы в группе.

Ф.И.

1

2

3

4

5

Балл

1. Высказал(а) идею, версию

2

2. Сформулировал(а) гипотезу

2

3. Уточнил(а) гипотезу

1

4. Задавал(а) вопросы

2

5. Отвечал(а) на вопросы

1

6. Составлял(а) алгоритм

2

7. Представлял(а) группу

2

8. Выполнял(а)

2

Итог

14

Оценка

5

Оценка за количество баллов: от 16 до 14 – «5»
от 10 до 13 – «4»
от 6 до 9 – «3»
от 0 до 5 – «2»
VII. Рефлексия.
На этом уроке я приобрел(а) следующие знания: ______________
Я научился(ась): _______________________
Я продемонстрировал(а) умения: ____________________

Мне нравятся такие уроки за ____________________