Конспект лекций по биофизике
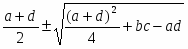 Конспект лекций по биофизике
Конспект лекций по биофизике
Биофизика как наука
Биофизика – это наука, изучающая физические и физико-химические процессы, протекающие в биосистемах на разных уровнях организации и являются основой физиологических актов. Возникновение биофизики произошло, как прогресс в физике, вклад внесли математика, химия и биология.
Живые огранизмы – открытая, саморегулирующаяся, самовоспроизводящаяся и развивающаяся гетерогенная система, важнейшими функциональными веществами в которой являются биополимеры: белки и нуклеиновые кислоты сложного атомно-молекулярного строения.
Задачи биофизики:
Раскрытие общих закономерностей поведения открытых неравновесных систем. Теоретическое обоснование термодинамических (т/д) основ жизни.)
Научное истолкование явлений индивидуального и эволюционного развития, саморегуляции и самовоспроизведения.
Выяснение связей между строением и функциональными свойствами биополиметов и других биологически активных веществ.
Создание и теоретическое обоснование физ-хим методов исследования биообъектов.
Физическое истолкование обширного комплекса функциональных явлений (генерация и распределение нервного импульса, мышечное сокращение, рецепция, фотосинтез и др.)
Разделы биофизики:
Молекулярная – изучает строение и физ-хим свойства, биофизику молекул.
Биофизика клетки – изучает особенности строения и функционирования клеточных и тканевых систем.
Биофизика сложных систем – изучает кинетику биопроцессов, поведение во времени разнообразных процессов присущих живой материи и термодинамику биосистем.
Термодинамика биологических процессов
Предмет и практическая значимость т/д биосистем. Подходы: феноменологический и детальный. Значение имеют т/д параметры только в исходном и конечном состоянии. Термодинамика – это наука, изущающая наиболее общие закономерности превращения различных видов энергии в системе.
Практическая значимость т/д в биологии. Позволяет оценить энергетические изменения, происходящие в результате биохимических реакций; рассчитать энергию разрыва конкретных хим связей; рассчитать осмотическое давление по обе стороны полупроницаемой мембраны; рассчитать влияние концентрации соли в растворе на растворимость макромолекул. Применяется для описания процессов, протекающих в электрохимических ячейках. Привлекается для обоснования теории возникновения и эволюции жизни на Земле.
Понятие т/д систем, виды т/д систем. Система – совокупность взаимодействующих между собой относительно элементарных структур или процессов, объединяющихся в целое выполнением некоторой общей функции, несводимой к функциям ее компонентов. Т/д система – часть пространства с материальным содержимым, ограниченная оболочкой.
а) изолированные (не обмениваются с окружающей средой ни веществом, ни энергией),
б) замкнутые (обмениваются энергией),
в) открытые (обмениваются веществом и энергией).
Параметры:
экстенсивные, зависят от количества вещества в системе (масса, объем),
интенсивные, не зависят от количества вещества в системе (давление, t0).
Первое начало термодинамики
Q = dU - W
Количество теплоты, поступающей в систему расходуется на увеличение внутренней энергии системы за вычетом совершенной работы.
W = pdV + W'max
Работа равна произведению давления на изменившийся объем плюс максимально полезная работа против внешнего давления по изменению объема системы.
Живые организмы не являются источников новой энергии. Окисление поступающих в живой организм питательных веществ приводит к высвобождению в нем эквивалетного количества энергии.
.................. – определение питательных веществ, поступающих в организм. Металлический сосуд с теплоизолирующими стенками в который помещаются исследуемые питательные вещества, затем их сжигают с помощью высоковольтных разрядов и измерают теплоту сгорания.
1 г белка – 5,4 ккал (4,1 ккал до мочевины)
1 г жира – 9,3 ккал
1 г углеводов – 4,1 ккал
Определение расхода энергии в течение суток. Метод прямой или непрямой калориметрии.
Прямой: Камера "ледяной калориметр". Теплоизолирующий материал, лед, лабораторное животное (человек). Энергия, высвобождающаяся из организма эквивалентна поступающей в организм
Непрямой: С полным и неполным газовым анализом.
ДК = выд СО2 в ед t / погл О2 в ед t
Производят сравнение состава и объема вдыхаемого и выдыхаемого воздуха. Используют мешок Дугласа. Для анализа используют газоанализаторы: ГА Холдейна: система стеклянных трубочек, поглощающая CO2 и O2. Сейчас ГА с поглощением световых потоков.
Нормальный дыхательный коэффициент 0,85±0,03. Нахождение КЭК (калориметрический эквивалент кислорода) – численно равен количеству энергии, высвобождающейся в организме при потреблении 1 л О2. Рисунок ДК = 1, КЭК = 5,05; 0,8; 4,8; 0,7; 4,69; 0,85; 4,86.
В клинических условиях используют неполный газовый анализатор, не считают СО2. Считают объем поглощенного О2 с помощью спирографа (аппарат метатест). Диаграмма под наклоном, из замкнутой системы постепенно уходит О2, Х отражает объем поглощенного O2 из системы 1 см≈400 мл. ДК принимается равным здесь 0,85.
1 л – 4,86 ккал
400 мл – х
Второе начало термодинамики
показывает в каком направлении происходит перемещение энергии в изолированных системах.
Энтропия S в т/д имеет троякий смысл:
если в т/д системе происходят процессы, связанные с выделением или поглощением тепла, то эта система при любой t0 способна поглотить некоторое дополнительное количество тепла. Величина, характеризующая тепловую емкость системы и является функцией t0 – S.
Тепловая емкость системы.
Т/д функция состояния системы, являющаяся мерой ее неупорядоченности.
лед S = 9.8, жидкость S = 16.7, газ S = 45.1
Мера вероятности системы, имеет статистический характер. Впервые установил Больцман.
S = k*lgW
Т/д вероятность – это количество микросостояний, возможных в пределах данного макросостояния. Все микросостояния, определяющие т/д вероятность имеют одинаковую математическую вероятность. Математическая вероятность – это среднее значение частоты появления события при массовых испытаниях.
В изолированных системах необратимые т/д процессы протекают в направлении возрастания энтропии. S полностью обратимых т/д процессов сохраняет постоянное значение. Теплота – это особый вид энергии (низкого качетва) не может переходить без потери в другие виды энергии. Тепловая энергия связана с хаотическим движением молекул, остальные виды энергии базируются на упорядоченном движении молекул.
Дриллюэн создал классификацию видов энергии по способности вида энергии превращаться в другие виды энергии.
– max эффективная, превращается во все другие виды энергии. Гравитационная, ядерная, световая, электрическая,
– химическая,
– тепловая. Деградация высших типов энергии в энергию низших типов – основное эволюционное свойство изолированных систем.
Рисунок
Т/д потенциал
Задачи т/д:
Определение величины работы, совершаемой в системе.
Характеристические функции состояния системы изменения которых численно равно полезной работе при условии постоянства определенных т/д параметров.
dU=dQ-dW
dS=dQ/T связ энергия
dQ=TdS
dWmax=TdS-dU
dWmax= dW'max полез +pdV
(бесполезная работа – работа против сил внешнего давления)
Wmax=TdS-dU-pdV
V, T = const
P, T = const
Рассмотрим первый случай
Если V, T = const, то pdV=0, то Wmax=TdS-dU=-d(U-TS)=-dF
F=U-TS – термодинамический потенциал Гельм-Гольци или свободная энергия Гельм-Гольца
Рассмотрим второй случай
Если P, T = const, то Wmax=-d(U+pdV-TS)=-dG
G – т/д потенциал Гиббса или свободная энергия Гиббса
В реальных условиях редко Р постоянно, а V системы изменяется, следовательно величины т/д потенциалов совпадают.
Т/д потенциалы делают заключения
Выполенение полезной работы при выполнении необратимого процесса всегда сопровождается рассеянием энергии, величину которой определяет произведением TdS, чем больше эта величина, тем более необратимым является процесс. Для абсолютно обратимых процессов
По знаку и величине т/д потенциала можно судить о направленности процесса, если в результате процесса величина т/д потенциалов уменьшается, такой процесс является самопроизвольным, идет с выделением энергии и называется экзергоническим, если т/д потенциалы увеличивается, то процесс идет не самопроизвольный, требует притока энергии извне и называется эндергоническим.
При достижении равновесия т/д потенциалы стремятся к минимальному значению.
Процессы превращений энергии и совершения работы могут протекать до тех пор пока свободная энергия не станет равна нулю, а энтропия максимальной. Такое состояние носит названия т/д равновесия.
Такое состояние в неживой природе является конечным состоянием, в направле6нии которого эволюционируют все т/д системы.
КПД
КПД – это отношение произведенной работы к изменению свободной энергии, затраченной на эту работу. КПД = W/dF 1 КПД может выражаться в абсолютных единицах или процентах. Согласно второму закону т/д, КПД обратимого процесса должно быть равно 1. КПД необратимых процессов < 1. КПД реальных биологических процессов < 1. Приблизительное значение КПД реальных биологических процессов:
Гликолиз – 36%
Ф/с –75%
Окислительное фосфорилирование – 55%
Сокращение мышц – 40%
Свечение бактерий – 96%
Градиенты
Биологические системы характеризуются наличием большого количества градиентов (осмотический, электрический, концентрационный…)
Градиент какого-либо т/д параметра изменяется с расстоянием
Рисунок
Ґ=ΔΤ/ Δυ
Ґ – направление от большого значения параметра к меньшему.
Биосистема способна совершать работу, если в ней имеется градиент. Градиент – своеобразное депо энергии.
F свободная энергия F = RTlnФ1/Ф2
Ф значение т/д параметров в 1 и 2 точках
Совершение работы в системе связано с реализацией этой свободной энергии. Если совершается работа, то градиент, за счет энергии которого это происходит, уменьшается, но параллельно возникает другой градиент противоположной направленности. При необратимых процессах величина второго градиента будет меньше, чем величина первого.
Применимость второго закона т/д для характеристики свойств био систем
Второй закон т/д был сформулирован для характристики изолированных систем. Реальные биологические системы являются открытыми.
Значение энтропии строго определено для равновесного состояния. Био системы в своем развитии проходят через целый ряд неравновесных состояний.
Энтропия и другие функции состояния могут быть определены в любой момент изменения неравновесного состояния или энтропии и др функций состояния является непрерывными и однозначными функциями т/д параметров и времени.
В открытой системе
dS=Q'/T+Q/T
Q'/T – тепло в самой ситеме
Q/T – тепло, которым система может обмениваться со средой
diS=Q'/T – внутренний источник энтропии
deS=Q/T – внешний источник энтропии
dS=diS+deS
Энтропия в системе изменяется за счет процессов производства энтропии в самой системе и за счет обмена энтропии между системой и окружающей средой.
diS>0 – необратимые процессы
dS/dt=diS/dt+deS/dt
Скорость изменения энтропии в системе равна сумме скорости продукции энтропии в самой системе и скорости обмена энтропией между системой и окружающей средой.
Скорость продукции энтропии в системе всегда больше 0, так как т/д процессы в ней необратимы.
Второй закон т/д для открытых систем
dS/dt>0 количество энтропии в системе возрастает
а) dS/dt>0; diS/dt>0;
б) deS/dt=0 нет обмена со средой, система изолированная;
в) deS/dt<0, deS/dt< diS/dt
В системе образуется некоторое количество энтропии, но часть энтропии оттекает в окружающую среду, но скорость оттока не велика и энтропия накапливается в системе.
dS/dt=0, стационарное состояние, кол-во энтропии постоянно
deS/dt<0, deS/dt=diS/dt
Вся энтропия, которая образуется оттекает в окружающую среду. Это состояние наиболее характерно для зрелых био систем.
dS/dt<0 общее количество энтропии в системе убывает
deS/dt<0, deS/dt>diS/dt
Энтропия в этой системе, но оттекает из системы больше, чем образуется, следовательно общее кол-во энтропии в системе уменьшается. В реальных био системах это встречается на стадии роста, развития и становления ситемы.
Стационарное состояние
Такое состояние т/д системы при котором ее параметры со временем не изменяются, но происходит обмен веществом и энергией. Для био систем часто встречается, но в то же время множество систем стремится к состоянию равновесия. Открытые системы могут переходить в состояние т/д равновесия
Стационарное состояние:
постоянный обмен энергией с окружающей средой
постоянно тратится свободная энергия на поддержание состояния
т/д потенциалы постоянны, G и F не равны 0
энтропия постоянна, но не максимальна
градиенты присутствуют
Термодинамическое равновесие
отсутствует поток вещества и энергии в окружающую среду и обратно
на поддержание этого состояния не затрачивается свободная энергия
работа способности системы равна 0, т/д потенциалы равны 0
энтропия максимальна
в системе отсутствуют градиенты
Механизмы устойчивости стационарного состояния в био системах. Теорема Пригожина
В любой открытой т/д системе постоянно образуется энтропия, в том числе и в био системе.
Пригожин сформулировал:
В стационарных состояниях при фиксированных внешних параметрах локальная продукция энтропии в открытой т/д системе стремится к минимальному значению.
Энтропия – мера рассеивания свободной энергии, следовательно любая открытая т/д система в стационарном состоянии стремится к минимальному рассеиванию свободной энергии. Если в силу причин система отклонилась от стационарного состояния, то вследствие стремления к системы к минимальной энтропии, в ней возникают внутренние изменения, возвращающие ее в стационарное состояние.
Механизмы саморегуляции систем
Функционируют по принципу обратной связи. Обратная связь – это понятие, обозначающее влияние выходного сигнала системы на ее рабочие параметры.
Рисунок. Различают положительную и отрицательную обратную связь. "–" чаще встречается в био системах, направлена на снижение влияния выходного сигнала на рабочие параметры системы. "+" усиливает влияние выходного сигнала на рабочие параметры системы в результате чего система может выходить из данного состояния.
Гомеостаз – постоянство многих параметров.
"–" мотонейрон, рисунок
"+" секреция желудочного сока. В желудке имеется желудочный сок, который вырабатывается до принятия пищи. Под действием желудочного сока начинается расщепление белков. В начальном отделе кишечника питательные вещества всасываются в кровь. Гормоны (гастрин, гистамин) всасываются в кровь, попадают в сосуды, кровоснабжающие желудок и активизируют его работу.
Механизм кругового возбуждения в нейронах ЦНС
Рисунок. "+" обратная связь имеет место в патогенезе заболевания. "Порочный круг" при инфаркте недостаток кислорода – нарушается питание сердца – гипоксия – нектоз тканей – изменение функций сердца – застой венозной крови – сердечная мышца страдает от недостатка кровоснабжения
Рисунок. В реальных био системах + и – обратная связь часто накладываются друг на друга, существуют параллельно. + обратная связь стремится вывести систему из стационарного состояния, при этом она будет переходить в новое стационарное состояние более выгодное при данных условиях. При этом оба стационарных состояния находятся в пределах физиологической нормы отклонений.
Типы переходных процессов
Рисунок
Кинетика биопроцессов
Динамические свойства биопроцессов
Каждая система состоящая из элементов будет характеризоваться динамикой, складывающейся из элементов. Кинетика биопроцессов – раздел биофизики, изучающий динамические свойства биопроцессов.
Параметры, меняющие свое значение со временем. Переменные величины: численность клеток, биомасса, концентрация отдельных веществ, трансмембранный потенциал. Изначально предполагается, что из изменение в каждый данный момент времени могут быть описаны соответствующими диф уравнениями.
Величины, значение которых с течением времени практически не изменяется. Это рН, t0, электропроводность ткани и т.д.
Пример: характеризует кинетику процесса в культуре клеток
Условия: имеется замкнутая популяция клеток, в которой происходят процессы их размножения и гибели. Питательные вещества присутствуют в избытке.
Вопрос: Как меняется численность клеток со временем? Может ли в ней установиться стационарное состояние, когда число клеток со временем меняться не будет?
Решается с помощью диф уравнения.
Количество клеток = N
dN/dt – ? зависит от V размножения и V гибели клеток.
dN/dt =Vразмножения – Vгибели = k1N – k2N = kN
k – коэффициент пропорциональности, определяется условиями. k1, k2: t0, кол-во пищи, концентрация солей, радиация). k = k1 – k2
dN = kN*dt
N = N0*ekt
N – количество клеток в любой момент времени,
N0 – количество клеток в начальный момент наблюдения t = 0,
е – основание натурального логарифма,
k – коэффициент пропорциональности,
t – время наблюдения за системой.
Если k > 0
t → ∞, N(t) → ∞ растущая
Если k < 0 (k2 < k1)
t → ∞, N(t) → 0 вымирающая
Если k = 0 (k2 = k1)
t → ∞, N = N0 cтационарная
Как изменится количество клеток в системе, если ограничить количество питательных веществ?
В этом случае изменение количества клеток в популяции со временем будет описываться логистическим уравненем Ферхюста:
dN/dt = kN*(Nmax–N/Nmax)
Nmax – максимально возможная численность популяции в данных условиях.
Рисунок. Логистическая кривая.
Начальная часть N << Nmax экспененциальный рост,
Вторая часть – изгиб в другую сторону N → Nmax количество питательных веществ ограничивает дальнейший рост количества клеток в популяции.
Основные особенности кинетики биопроцессов
В биокинетике в качестве переменных величин выступают не только концентрации веществ, но и другие параметры.
Биосистема пространственно гетерогенна, следовательно условия действия реагентов могут различаться в разных точках системы и переменные изменяются не только во времени, но и в пространстве.
Существуют специфические механизмы саморегуляции действия по принципу обратной связи.
Трудности биокинетики связаны так же с тем, что она описывает процессы открытых систем.
Схема системы с отрицательной обратной связью
ОУ – объект управления,
РВ – регулируемая величина,
ИУ – измерительное устройство (измерение параметров регулируемой величины)
АС – аппарат сравнения,
ОС – обратная связь,
f – сигнал от высших центров регуляции.
Простейшая кинетическая модель открытой системы
. Модель системы в которой происходит обмен веществ "а" и "b" с окружающей средой, внутри обратимые реакции превращения "а" в "b", во внешних резервуарах концентрация этих веществ постоянна и равна соответственно А и В.
da/dt = k1(A–a)–k2(a–k–2b)
db/dt = k2a–k3(b–B)–K–2b
Для стационарного состояния будет соблюдаться условие: da/dt = 0, db/dt = 0.
"а" стационарное и "b" стационарное не зависят от начальных условий, то есть от значений "а" и "b" в момент t = 0. "а" стационарное и "b" стационарное определяются только величинами констант k с 1 по 3 и концентраций веществ во внешних резервуарах системы, то есть А и В.
Вывод:
В каком бы начальном состоянии ни находилась система, в ней в конце концов установится один и тот же стационарный режим при котором а = а стационарное, b = b стационарное. Это свойство эквивалентности стационарных состояний. Оно присуще открытым системам и постоянно встречается при изучении свойств биополимеров.
Качественный анализ кинетической модели
Основная идея метода заключается в отказе от нахождения точных аналитических решений диф уравнений. Вместо этого используются качественные характеристики динамического поведения системы: устойчивость или неустойчивость стационарного состояния, переходы между стационарными состояниями, наличие колебательных движений в системе, качественная зависимость поведения системы от критических значений параметров. Наиболее важным свойством стационарного состояния является его устойчивость, она определяется спосбностью системы самопроизвольно в него возвращаться после внесения внешних возмущений, отклоняющих систему от исходно стационарной точки.
Очевидно, чтобы сделать заключение об устойчивость стационарного состояния необходимо иметь соответствующие критерии.
Бассейн с водой открытая система. С определенной Vпр в него поступает вещество а, но оно с определенной Vот из системы истекает. Vпр постоянна, Vпр = V0 = cosnt. Чтобы выяснить с какой скоростью меняется количество вещества в системе, нужно вычислить: da/dt = Vпр – Vот = V0 – ka, k – const Vот.
Рисунок. Стационарное состояние в т. а отвечает условию, что V = cosnt = 0. В стационарной точке da/dt = 0. Количество вещества в системе постоянно. Качетвенный анализ дается графическим методом. Случайные отклонения а будут компенсироваться системой. Стационарное состояние а устойчиво.
Качественный критерий устойчивости стационарного состояния Ляпунова
Если система находится в состоянии равновесия, то точка, изображающая местоположение исследуемого показателя на графике будет името постоянное значение координат.
dx/dt = 0, dy/dt = 0
x(t) – const, y(t) – const
Такая точка получила название особой точки. Она показывает местоположение на графике стационарной системы. Если система по каким то причинам выходит из состояния равновесия, то изображающая точка сместится из особой точки и начнет двигаться по плоскости в соответствии с изменением координат х и у.
В этой ситуации: dx/dt = p; p = f (x;y); dy/dt = q; q = f (x;y).
p и q – непрерывные функции, определенные в данной области плоскости. В соответствии с критерием Липунова состояние равновесия устойчиво, если для любой области допустимых отклонений от состояния равновесия () можно указать область , окружающую состояние равновесия и обладающую тем свойством, что ни одно движение преображающей точки, начинающееся в пределах области никогда не достигнет границ области .
При этих условиях стационарное состояние устойчиво.
Если же для какой то области не существует области , то равновесие не устойчиво.
Во многих системах существует не одно, а несколько стационарных состояний, свойства их чаще всего различаются. И это в первую очередь касается их устойчивости, поэтому в данных ситуациях задачей качественного анализа является определение устойчивости всех стационарных состояний и условий перехода между ними.
Редукция числа уравнений. Принцип узкого места
Желательно отразить в системе уравнений все ее наиболее значимые свойства. Но вместе с тем системы диф уравнений из большого их числа, являются перегруженными. Такая модель чересчур детализирована, следовательно наиболее оптимальными моделями, характеризующими основные свойства систем являются модели, состоящие из небольшого числа диф уравнений (предположительно из двух).
Принцип узкого места (ПУМ) основан на разделении всех переменных, характеризующих свойства системы на быстрые и медленные. Характерное время процесса – отражает время развития процесса. процессов ферментативного катализа 10–1 – 10–6 с, процессы физиологической адаптации, для них несколько минут и больше, процессы репродукции в этой же системе, для них несколько минут и больше. – величина противоположная скорости. V=1/. В пределах одной отдельной цепочки взаимосвязанных реакций всегда имеются наиболее медленные и наиболее быстрые стадии.
Согласно ПУМ общая скорость всей цепи реакций определяется наиболее медленной стадией (она и есть узкое место), она имеет самое большое , Vmin. Общее время всей цепи реакций (всего процесса) будет мало отличаться от характерного времени узкого места. Чтобы воздействовать на время процесса нужно воздействовать на узкое место.
При внешних возмущениях в системе наблюдаются изменения как быстрых, так и медленных перменных, однако эти изменения протекают с разной скоростью. В устойчивой системе быстрые переменные быстро отклоняются от своих начальных значений, но быстро в них возвращаются. Медленные переменные изменяются в ходе длительных переходных процессов, определяющих динамику всей системы. Фактически быстрые переменные колеблются возле своих стационарных значений. Поэтому вместо диф уравнения, описывающего динамику быстрой переменной можно записать алгебраическое уравнение, отражающее ее стационарное значение, что приведет к постоянному уменьшению числа диф уравнений в системе, останутся лишь те, что описывают наиболее медленные процессы.
dx/dt=AF(x;y)
dy/dt=Q(x;y)
A>>1 A*F >> 1 x быстрая переменная (dx/dt быстрая величина, скорость х велика)
делить на А
(dx/dt)=F(x;y), где =1/A, <<1, 0, F(x;y)=0, =0
Следовательно у является управляющим параметром, влияющим на координаты в стационарной точке. В био системах роль узкого места могут выполнять разные звенья цепи в зависимости от условий.
Например, ф/с:
Рисунок
В данном процессе меняется управляющая стадия в зависимости от освещения. При плохом освещении узким место ф\с-а являются начальные фотохимические стадии поглощения и трансформации энергии и света в пигментном аппарате. Скорость этих процессов не зависит от t0 в промежутке от +5 до +300 С. При хорошем освещении узким местом ф\с-а являются темновые процессы переноса электрона и поглощения воды.
Эти процессы не справляются с потоком электронов, поступающих от пигментного комплекса, что приводит к насыщению ф\с-а (световое насыщение), эти процессы являются ферментативными, поэтому их скорость зависит от t0. И скорость ф\с-а будет увеличиваться с ростом t0.
Типы динамического поведения био систем
Система двух диф уравнений, модель хар-ся отсутствием перегруженности, на их основании можно качественно провести анализ.
dx/dt=P(x;y)
dy/dt=Q(x;y)
Используется метод фазовой плоскости
Фазовая плоскость – это плоскость с осями координат, на которых отложено значение переменных (х;у), отражающих состояние системы, таким образом каждая точка этой плоскости будет соответствовать определенному состоянию системы
х0, у0 – начальные состояния системы.
Траектория из последовательности точек, каждая из которых будет характеризовать состояние системы в любой определенный момент времени.
Последоват. сов-ть точек на фазовой плоскости, отражающая значение переменных (х;у) на пути перехода – это линия, получившая название фаз???
Изображающая точка – точка на фазовой плоскости, отражает состояние системы в определенный момент времени. Фазовый портрет – совокупность фазовых траекторий, отражающих качественные черты поведения системы во времени.
P(x;y)=0 –
Q(x;y)=0 –
стационарное состояние
Для нахождения особой (стационарной) точки, необходимо построить на фазовой плоскости кривые P(x;y)=0; Q(x;y)=0. Очевидно, особая точка будет находиться в месте пересечения этих кривых.
dx/dt=k1A – k1x+k2y-kx=P(x,y)
dy/dt=k2x-k-2y-k3y+k3B=Q(x,y)
y=-C1x+C2
y=C3x+C4
C – коэффициент пропорциональности
Графики могут пересекаться в нескольких точках (если это кривые), следовательно существует несколько стационарных состояний.
Фазовый портрет триггерной системы
Типы устойчивости особых точек
Важной задачей является определение устойчивости особых точек. Производится по виду правых частей исходной системы уравнений. Об устойчивости стационарного состояния системы судят по поведению системы в случае небольшого отклонения от стационарной точки.
=x-xст
=у-уст
Для определения характера устойчивости необходимо одновременно учитывать поведение во времени отклонений и . Существуют специальные уравнений, описывающие и .
(t)=C11e1t+C12e2t
(t)=C21e1t+ C22e2t
Особый смысл имеют 1 и 2 – это экспоненциальные показатели
1,2 =
a,b,c,d – значения частных производных в точке (хстац;устац). От вида 1,2 зависит поведение отклонений и соответствующих поведению х и у в особой точке (окресностях). 1,2 это либо действительные числа, либо комплексно-сопряженные (если под знаком корня дробь).
1 и 2 < 0 то есть они являются действительными отрицательными числами, значение и будут со временем снижаться, то есть отклонение системы от особых точек со временем будет . В этом случае стационарное состояние является устойчивым, а особая точка называется устойчивый узел, такой точке соотвествует особый тип фазового портрета.
Рисунок. Система будет возвращаться по какой-то траектории в стационарное состояние.
1 и 2 > 0, действительные положительные числа и будут увеличиваться со временем, следовательно первоначальное состояние было неустойчиво и система все дальше будет отклоняться от состояния равновесия.
Неустойчивый узел. Фазовый портрет такой же, но стрелки на периферию.
1 и 2 действительные числа разных знаков.
Рисунок. Тогда на фазовом портрете системы будет существовать особая точка типа "седла". Сопаратиссы.
Из любого начального положения на фазовой плоскости кроме особой точки сепаратисс система будет удаляться из стационарного состояния. Если 1 и 2 комплексно-сопряженные числа, то изменения во времени и носят колебательный характер. Частные случаи:
Действительные 1 и 2 < 0,
Рисунок. Re<0, то колебания ситемы носят затухающий характер. Особая точка на фазовом портрете будет называться устойчивый фокус.
Действит 1 и 2 > 0,
Рисунок. Cтрелки на фазовом портрете направлены наружу, неустойчивый фокус
Re 1 и 2 = 0,
Рисунок. В этом случае 1 и 2 превращаеются в мнимые числа, фазовые траектории будут представлять собой эллипсы, не проходящие через начало координат. В начале координат находится неустойчивая точка (центр). Необольшие возмущения в системе переводят ее с одной траектории на другую, то есть изменяется амплитуда колебания.
Первые пять типов состояния равновесия являются грубыми, так как их характер не изменяется существенно при небольших изменениях правых частей исходного уравнения, а так же из проиводных первого порядка. Эти типы устойчивости характерны для био систем, так как они должны определенным запасом грубости. Такой запас позволяет им сохранить основные динамические свойства при умеренных внешних воздействиях.
Биологические триггеры
(Триггер – спусковой крючок у оружия)
Любая триггерная система способна переключаться с одного режима на другой. Ф.п. стриггер системы характризуются как минимум двумя стационарными точками (А и С)
Рисунок. 2 вида переключения.
1) силовое переключение осуществляется при значительном изменении переменных х или у.
связан с наличием управляющего параметра. Он оказывает влияние на величину обеих переменных х и у.
После этого можно восстановить значение управляющего парметра, что приведет к восстановлению исходного вида фазового портрета, однако система при этом остается в устойчивой точке С.
Колебательные процессы
характерная черта био систем. Частые колебания промежуточных продуктов био-хим реакций, численности видов, потенциала мембраны и т.д.
В любом организме существует набор био-хим процессов, в их основе лежат внутренние свойства системы. Причины колебаний во внутренних динамических свойствах системы. Автоколебательные процессы. Тип фазового портрета – устойчивый предельный цикл. Замкнутая траектория, не проходящая через начало координат. С наружной и внутренней стороны подходят спиральные траектории. Система работает в устойчивом колебательном режиме. Если система в силу внешних воздействий выйдет из такого режима, то в силу своих свойств она вернется на замкнутую траекторию. Возвращение будет осуществляться по спиральной траектории. Переход движения вдоль траектории предельного цикла в автоколебательной системе не зависит от начальных условий.
Распределение биологической системы
В био кинетике предполагается изменение переменных не только во времени но и в пространстве, в биохимии важнее изменения во времени. В отличие от точечные, такие модели, которые учитывают измениения переменных во времени и в пространстве, называются распределенными. Таким образом, в распределенных системах будут 2 параллельных процесса – хим превращения в отдельных точках пространства и процесс диффузии веществ из области высокой в область низкой концентрации. То есть происходит перенос вещества между соседними элементарными отсеками. В реальных био системах часто существует пространственное распределение источников энергии. Эти системы называются активные распределенные системы.
Анализ распределенной системы:
Состояние системы уравнений, отражающих хим реакцию и диффузию реагента. Max простой пример распределенной системы – система, в которой имеется одна переменная Х, одновременно участвующая в хим процессе и диффунцирующая вдоль узкой трубки. r – учитывается размер трубки. Диффузионный поток вещества – масса вещества, проходящего через единицу площади перпендикулярной к направлению диффузии (ось х), пропорционален градиенту вещества, взятому с обратным знаком.
I = –D*ds(r,t)/dr,
D – коэффициент диффузии, t – время, C – концентрация, изменение концентрации во времени за счет диффузии в элементарном объеме трубки, заключенном между точками r и r+r, зависит от разности потоков в точках r и r+r. Если D const, то изменение С во времени (скорость изменения С) =
dc/dt=D*d2c(r,t)/dr2,
уравнение диффузии, оно описывает скорость изменения С в системе, в которой происходит только диффузия вещества. Но по условию, в распределенной системе параллельно происходит и хим превращение вещества. Величиной, отражающей хим превращение в системе, является величина точечных членов, которая обозначается, как функция концентрации.
dc/dt=f(c)+D*d2c(r,t)/dr2,
выражение отражает химическое превращение и изменение концентрации. В этой системе изменения происходят только по оси Х. В системах, в которых происходят колебательные процессы невозможно отразить их поведение с помощью одного уравнения, поэтому в данном случае используются базовые модели с двумя переменными:
dx/dt=P(x,y)+Dx*d2x/dr2,
dy/dt=Q(x,y)+Dy*d2y/dr2
Такая базовая модель позволяет качественно описать процессы самопроизвольного возникновения волн и структур в распределенных системах. В общем, они называются самоорганизацией, она возникает, когда в системе появляется неустойчивость, приводящая к потере исходного распределения веществ во времени и пространстве. Вместо этого устанавливается новое распределение вещство во времени и пространстве. Характер самоорганизации зависит от функции f (P,Q) (точечных членов) и D, в частности существуют следующие виды самоорганизации:
Распределение возмущения в виде бегущего импульса (нервный импульс).
Стоячие волны.
Синхронные автоколебания разных элементов во всем пространстве системы.
Стационарные неоднородные распределения переменных в пространстве (диссипативные структуры).
Генерация волн автономными источниками импульсной активности (локальные кратковременные флуктуации переменных).
Общим условием возникновения процессов самоорганизации всегда является появление неустойчивости в исходной распределенной системе.
Молекулярная биофизика
Предмет молекулярной биофизики
Изучает строение и физ хим свойства биофункциональных молекул (прежде всего биополимеров). Основной задачей мол биофизики является вскрытие физических механизмов, ответственных за био функциональность этих молекул (напимер, ферментативная активность белков).
Методы: ЭПР, ЯМР, рентгеноструктурный анализ, биохимические технологии.
Стремится выяснить основные детали структуры и функции молекул. Основное свойсто – хиральность биомолекул. Большинство молекул, содержащих больше 3х атомов, не имеют ни центра, ни плоскости симметрии. Их можно назвать диссиметричные, или хиральные. В био молекулах связи С могут быть заняты, как одинаковыми, так и разными группами.
СХ2НZ молекула будет иметь плоскость симметрии. Рисунок
Из 20 а-к хиральность свойственна 19, ей не обладает глицин. В процессе хим синтеза из исходных симметричных молекул хиральное вещество образуется всегда в виде рацимической смеси, которое содержит по 50% молекул D, L – форм хирального вещества. Состояние с максимальной энтропией.
В живой природе имеется фиксация в био структурах какой-либо одной формы хиральных веществ (например в ДНК и РНК всегда D-форма углеводов). С позиции биофизики это объясняется фиксацией информации, то есть выбор одного антипода равнозначен информации в 1 бит.
L-аспарагиновая кислота не имеет вкуса, D-аспарагиновая кислота сладкая. Существуют некоторые яды, вызывающие токсический эффект в одной форме и безвредные в другой. Это свойство открыто в 1848 г. Л. Пастером.
Виды взаимодействий биологических молекул
Основой структуры биологических молекул являются сильные связи – химические ковалентные связи. Биомолекулы отличаются высоким содержанием С, между С–С сильная связь, энергия разрыва равна 328,9 кДж/моль. Сильные связи присутствуют там, где содержатся мономерные звенья. Сильные связи образуются внешними электронами атомов, поэтому для исследования их особенностей используется раздел Квантовая Химия. Но есть важный недостаток сильной связи, они создают жесткий каркас.
Слабые связи основаны на действии невалентных слабых сил, и на их базе формируются биомолекулы. Различаются взаимодействия белковых молекул с другими видами молекул. На базе слабых связей осуществляется тонкая регуляция химических взаимодействий, компартментализация, градиент.
Слабые связи характеризуются преобладанием сил притяжения на больших расстояниях и преобладанием сил отталкивания на близких расстояниях.
Рисунок 1
График зависимости потенциальной энергии слабого взаимодействия от расстояния между двумя взаимодействующими частицами молекулярной природы.
R0 – минимальный потенциал энергии взаимодействия. В точке, соответствующей R0 силы притяжения равны силам отталкивания. Если расстояние меньше R0 , то преобладают силы отталкивания. Если расстояние больше R0, то преобладают силы притяжения. R0 оптимальное расстояние, на котором и будут находиться взаимодействующие частицы.
Вторичная структура биомолекул зависит от различных видов слабых связей.
Ионное взаимодействие.
взаимодействие между двумя ионами с зарядами l1 и l2 . Потенциальная энергия в данном случае находится по формуле:
Uион=(l1 + l2)/R,
R – расстояние между ионами,
– диэлектрическая проницаемость среды,
l1 и l2 – заряды ионов.
Величина Uион зависит от зарядов ионов. Если заряды противоположны, то Uион<0 – притяжение, если заряды имеют одинаковый знак – силы отталкивания преобладают.
Ионные взаимодействия: между ионогенными группами белков, малыми противоионами, фосф группами нуклеиновых кислот и катионами.
Ион-дипольные взаимодействия.
взаимодействия между ионами и полярными группами молекул.
Энтропия этого взаимодействия определяется зарядом иона, дипольным моментом взаимодействующей с ним атомной группы, а так же расстоянием между ними.
P = e*l → U = e*P/ε*R
P – дипольный момент,
l – расстояние между центрами диполя.
Ориентационное взаимодействие
взаимодействие между двумя диполями или группой диполей, присутствующих в некоем участке пространства Рисунок
a) между двумя диполями:
P1 = e1*l1,
P2 = e2*l2,
e – заряд электрона, l – расстояние м/д центрами диполя.
Uориент= 2P1*P2/R3.
б) группа диполей не может выстроиться в антипараллельное положение, будет наблюдаться некоторое усреднение взаимодействия между ними.
Uсред=2P12P22/3kTR6,
k – постоянная Больцмана,
Т – абсолютная температура.
Индукционное взаимодействие
постоянные дипольные молекулы или атомные группы (Р1) индуцируют в другой молекуле или атоме дипольный момент (Р2), с которым он и взаимодейтвует.
Способность индуцировать диполи в других молекулах определяется напряденностью электромагритного поля первого диполя. Р2 дипольный момент будет зависеть от Е1 напряженности поля.
Р2 = а*Е1, а – поляризуемость.
Поляризуемость – это способность электронной оболочки смещаться под действием электронного поля. а = 10–24 см3 (размер самой электронной оболочки)
Uинд=2aP2/R6
индукционное взаимодействие не зависит от температуры.
Если в среде существует первый диполь, наводящие другие, то он вряд ли будет единственым, следовательно индукционные взаимодействия в значительной мере усредняются и компенсируются друг другом.
Дисперсионные взаимодействия
взаимодействия валентно насыщенных электронных оболочек атомов и молекул.Существует между молекулами газов (N2, CO2, O2). И именно дисперсионными взаимодействиями объясняется непредельность поведения этих газов. Дисперсионные взаимодействия лежат в основе структуры молекул кристаллов.
Любой электрон является своеобразным гармоническим осциллятором (когда электрон движется по своей орбите, он является источником волн). Если электрон не взаимодействует с другими электронами, то длину его волны можно рассчитать W0 – исходная частота осцилляции. Во время дисперсионных взаимодействий происходит взаимодействие между двумя такими осцилляторами, при этом длина волны первоначального колебания начинает изменяться, то есть возникает как бы два различных колебания с частотами, отличающимися от первоначальной тем, чем больше взаимодействие.
Uдис. = - ¾* ћ*W0*a2/R6
ћ – постоянная Планка,
R – расстояние между взаимодействующими частицами,
а – поляризуемость.
В основе дисперсионного взаимодействия лежат не электростатические, а квантовомеханические силы. Это доказал Лондон.
Ориентационное, индукционное и дисперсионное взаимодействие называется ВанДер-Ваальсовым взаимодействием. ВанДер-Ваальсовы силы ответственны за образование конденсированной жидкости, а так же они описывают взаимодействие на разделе фаз (твердый и жидкий).
6. Водородные связи –
специфическая связь, которая создается атомом Н, который находится в группах ОН, NH, FH, ClH и иногда SH, причем Н связывает эти группы с валентно насыщенными атомами N2, O2 и F.
Водородные связи определяют структуру и свойства воды, как самого главного и основного расворителя в биосистемах. Водородные связи участвуют в формировании макромолекул, биополимеров, а так же связях с малыми молекулами.
Uвод = 4-29 кДж/моль
Основной вклад в водородные связи вносят электростатические взаимодействия, но они не сводятся к ним. Протон движется вдоль прямой, соединяющей экектоотрицательные атомы и испытывает различное влияние со стороны этих атомов.
Рисунок
Этот график – частный случай, связь между N-H...N и N...H-N. R – расстояние между взаимодействующими частицами. 2 минимума свободной энергии располагаются возле первого или второго взаимодействующего атома N.
7. Гидрофобные взаимодействия
базируются на силах специфического отталкивания между неполярными атомными группами и молекулами воды. Гидрофобные взаимодействия определяют свойства воды, как конденсированной жидкости. Эти взаимодействия объясняются энтропийным эффектом (реализуется наиболее верояное состояние). Гидрофобное взаимодействие определяет структуру белковых молекул, а также многих надмолекулярных систем.
Особенности строения воды
Вода является средой с большим количеством водородных связей, именно они определяют особые свойства воды:
ее способность сохранять жидкое состояние в широком диапазоне t0,
низкую t0 образования льда.
Для льда характерно строго упорядоченное расположение молекул воды, под тетраэдрическими углами. Каждая молекула имеет 4 водородных связи между соседними молекулами. Это рыхлая структура. Когда из льда образуется вода, то эта структура разрушается, в жидкой воде встречаются молекулы с 4,3,2,1 и 0 водородными связями. Водородные связи в жидкой воде характеризуются широким набором углов и длин.
Потенциальная энергия. U вод. связ. жидк. воды – непрерывная функция угла межмолекулярной водородной связи и геометрических характеристик молекулы воды.
Существует несколько моделей структуры воды
Разработана Айзенбергом и Кауцманом. Особое внимание обращается на масштаб времени наблюдения за структурой. Удалось обнаружить 3 структуры воды:
если сделать снимок с длительностью экспозиции намного меньше, чем период колебаний молекул воды (<<кол., =2*10–13 c), то мы регистрируем М-структуру, которая характеризуется малой упорядоченностью.
если продолжить >>кол., но намного меньше времени вращения тел диффузии t=10–5 с, то удается пронаблюдать К-структуру. Она характеризуется упорядоченным расположением молекул воды, но случайностью ориентации.
при >>периода вращения диффузии получается Д-структура. Она характеризуется регулярным расположением молекул воды и их правильной, закономерной ориентацией.
Кластерная модель Шерага.
Жидкая вода состоит из отдельных молекул и структурно связанных кластеров. Кластеры постоянно распадаются и возникают вновь. Это создает усредненное окружение для каждой отдельно взятой молекулы воды, - слабо учитывает молекулы воды в молекулярных группах.
Модель Самойлова
рассматривает структурные изменения воды при различных температурах. Предположим, что во время таяния льда, оторвавшаяся молекула воды заполняет пустоты кристаллической решетки, при этом увеличивается удельный вес. Максимальный удельный вес воды наблюдается при +40С, при более высокой t0 происходит увеличение амплитуды колебаний молекул воды, увеличение занимаемого ею объема и снижению плотности.
Растворимость различных веществ в воде
В воде хорошо растворяются электролиты вследствие высокой диэлектрической проницаемости воды, так же вещества с большим дипольным моментом и вещества, способные образовывать водородные связи с молекулами воды.
Рисунок. Нерастворимые вещества в воде: различные углеводороды, масла, жиры. Это объясняется тем, что контакты между молекулами Н2О–Н2О и С6Н6–О молекулами оказываются более выгодными, чем С6Н6–Н2О. В любой ситуации, когда свободная энергия раствора меньше свободной энергии воды и растворимого вещества, данное вещество хорошо растворяется в воде (и наоборот).
Гибкость полимерных молекул
Молекулы биополимеров сложны и обладают набором свойств.
Инфрмационность полимерных молекул базируется на разнообразии мономерных звеньев. Любая био молекула представляет собой своеобразный био текст и несет в себе некоторый объем информации. Для биофизики важны свойства и информация молекул, для этого информационные молекулы сравнивают с модельными молекулами. К ним относят каучук, он обладает эластчностью (свойство, характерное для биополимеров). Эластичность – это способность полимера испытывать большие упругие деформации (достигающие 100%) при малом модуле упругости. Но в каучуке нет информации, так как он состоит из мономеров, это достоинство используется для сравнения с биополимерами для выяснения биофункции.
Молекулы каучука подчиняются законам Гука
σ = ε(L0–L)/L0,
напряжение σ равно модулю упругости ε, L0 – начальная длина, L – конечная длина. Каучук обладает некоторыми свойствами идеального газа. Энтропийный характер упругости для идеального газа означает, что при движении поршня внутри цилиндра и росте давления в нем, мы переводим его из более вероятного состояния в менее верояное сжатое состояние, понижается энтропия газа. С каучуком происходит тоже самое. Между элементами каучука, связанными в линейную цепь, существуют связи между которыми могут происходить вращения, в результате чего изменяется конформация цепи. В биополимерах так же есть такие связи: С-С, С-N, С-О, вокруг которых могут происходить вращения – молекулы биополимеров обладают конформационной лабильностью. Эти конформационные свойства играют важную роль, так как на них базируются все функционально важные свойства биополимеров.
Клубок, глобула и условия их существованиия
Рисунок. Благодаря вращению вокруг единичных связей, цепочка биополимеров сворачивается самопроизвольно в клубок.
N – количество звеньев
l – средняя длина звена (длины звеньев не равны)
h – расстояние между началом и концом
Нужно найти размер клубка.
h=0, так как конец цепочки может равновероятно находиться в любом месте по отношению к началу, поэтому находят h2 , так как он не равен нулю.
h2=Nl2*(1+cosQ)/(1-cosQ)
рисунок. Q – угол вращения, угол между продолжением и звеном цепи. h2 характеризует размеры полимерного статического клубка. Состояние клубка является наиболее вероятным состоянием биополимера. Ему соответствует максимальная энтропия.
Есть прямые доказательства существования клубка биополимеров. Фотографии. При сворачивании в клубок между атомами возникают взаимодействия двух типов.
Взаимодействия ближнего порядка – взаимодействия между соседними полимерными звеньями.
Дальние взаимодействия, очень объемные эффекты. Они возникают между атомами, которые в цепочечной структуре биополимера отстоят далеко друг от друга, но вследствие изгибов цепи оказались на небольшом расстоянии. Вследствие объемных эффектов плотность звеньев в пространстве, занятом молекулой биополимера, может изменяться от точки к точке. Существует пространственная корреляция. В состоянии клубка флукитуация (колебания) плотности имеет порядок самой плотности. Однако наличие объемных взаимодействий может привести к такому состоянию в котором флуктуация плотности окажется малой по сравнению с плотностью. Такое состояние носит название глобулы.
Условия существования клубка и глобулы.
Важны заряды, расстояния между мономерами и t0. Увеличение t0 способствует отталкиванию звеньев, снижение приводит к притягиванию. Существуют t0 при которых отталкивание между мономерами полностью компенсируется их взаимным притяжением. Такая t0 соответствует точке Гетта Q (тепла). В Q-точке макромолекула представляет собой клубок с размерами R ≈ lN1/2. При увеличении t0 выше Q-точки возрастают силы отталкивания между мономерам и R > lN1/2 но макромолекула будет в виде клубка. При снижении t0 ниже Q-точки в объемных взаимодействиях будут преобладать силы притяжения между мономерам. Это приведет к конденсации полимерного клубка в плотное слабо флуктуирующее образование, которое называют глобулой, R ≈ lN1/3. Таким образом изменение t0 приводит к изменению размеров макромолекулы, изменению плотности мономеров, и как следствие к изменению энергии взаимодействия и изменению агрегатного состояния.
Свободная энергия взаимодействия звеньев зависит от плотности агрегации этих звеньев.
Рисунок. Вид клубка при нулевой температуре, F- свободная энергия, n – число звеньев. В состоянии клубка молекула имеет min свободной энергии при N ≠ 0. Где F=0 будут осуществляться обратимые переходы между клубком и глобулой. Переходы могут быть двух видов:
переходы первого рода: при изменении t0 наблюдается тепловой эффект, S и внутреняя энергия изменяются скачками.
фазовый переход второго рода: без тепловых эффектов. Теплоемкость при этом изменяется скачкообразно, S и внутреняя энергия изменяются плавно. В результате удельный V системы не испытывает скачкообразность изменений.
Таким образом вид перехода определяется свойствами макромолекулы. В случае жесткой полимерной цепи переход клубок-глобула осуществляется как фазовый переход первого рода, в случае гибкой цепи – как фазовый переход второго рода.
Рисунок. Графическая зависимость плотности мономерных звеньев от t0. n – плотность мономерных звеньев, 1 жесткая цепь, 2 гибкая цепь. В случае гибкой цепи нет конкретной Q точки, выделяется Q лишь область. В реальных био молекулах гибкость цепи может изменяться в силу различий отдельных участков.
Статистическая картина фазового перехода усложняется в реальных молекулах. Структуры перестройки зависят от физической природы взаимодействий между мономерными звеньями и необязательно усредняются по всему объему, занятому данной молекулой.
Статистическая теория полимерных цепей
СТПЦ берет начало в 50х годах ХХ века из Ленинграда. Основная идея СТПЦ заключается в том, что в полимерной цепи реализуются не любые повороты атомных групп вокруг единичных связей, но существуют лишь определенные поворотные изомеры. Конформацию ротомеров можно установить, если мы знаем химическую структуру цепи.
Рисунок. Этан. Более выгодня транс-конформация, так как вокруг единичной связи вращается молекула и меняется Е потенц.
Рисунок. Графическая зависимость Е потенц. от угла вращения. φ=0 при транс. При поворотах вокруг единичной связи молекула этана преодолевает своеобразный энергетический барьер = 12200 Дж/моль.
Величина энергетического барьера имеет в своей основе энергию дисперсионных сил, если взаимодействующие звенья не полярны; если же они полярны, то кроме дисперсионных сил, свой вклад вносят ориентационные и индукционные силы.
Рисунок. Бутан. СН3–СН2–СН2–СН3 энергетически более выгодна транс-конформация, при которой СН3 группы находятся на max расстоянии друг от друга. Время превращения одного ротомера в другой 10–10 с. Ротомеры нельзя разделить, они непрерывно переходят из одной конформации в другую.
Биофизика клетки. Мембранология.
Все клетки окружены цитоплазматической мембраной, которая представляет собой функциональную структуру, толщиной в несколько молекулярных слоев, которая ограничивает цитоплазму и большинство внутриклеточных структур, а так же образует единую систему канальцев, складок и замкнутых полостей, расположенных внутри клетки. Толщина редко превышает 10 нм, в этой структуре плотно упакованы липиды и белки, поэтому сухой вес мембраны составляет более ½ сухого веса клетки.
В середине XIX века Дюбуа-Реймон впервые сообщил, что между внутренней и внешней поверхностью кожи лягушки имеется разность потенциалов. Моль ввел термин "мембрана" , он изучал цитоплазму клеток растений и выяснил, что она окружена полупроницаемой мембраной. 1877 г. Пфейфер-ботаник, исследуя явление осмоса, пользовался как естественной, так и искусственной мембраной из осадочного ферроцианида. Cu → cходнства между ними → естественная мембрана участвует в явлении осмоса. Позднее стали говорить о генерации биопотенциала мембраны (конец XIX века). 1902 г – Бернштейн – мембранная теория потенциала покоя и потенциала действия → развитие мембранологии. Хаксли, Ходжкин и К0 впервые показала, что потенцилы покоя и действия базируются на избирательной проницаемости мембраны к определенным ионам (К+) – неодинаковое распределение ионов по обе стороны мембраны, в основе чего лежат процессы активного транспорта ионов через мембрану. С участием мембраны связаны: фоторецепция, рецепция, БАВ, передача нервного импульса, синтез ДНК.
Химический состав мембраны
Достаточно высокое содержание липидов, они составляют мембранную матрицу; белки составляют вариабильную часть; углеводы в виде гликопротеидов и гликолипидов. В мембране всегда находится небольшое кол-во воды (важная роль).
Липиды мембраны:
Классификация
Классы:
Липиды – производные глицерина. Кефалины – фосфодиэтаноламин, Лецитин – фосфатидилхолин.
Липиды – производные сфингозина. Сфингомиолин, цереброзиды.
Стерины – холестерин, β-ситостерин, эргостерин, зимостерин и т.д.
Минорные липиды - β-каротин, витамин К.
Группы:
Нейтральные липиды – холестерин, триглицериды.
Цвиттерионы – 2 заряда диполя – фосфотидилэтаноламин, фосфотидилхолин.
Липиды – слабые кислоты, фосфотидилсерин.
Липиды – сильные кислоты – фосфотидиловые кислоты и сульфокислоты.
Мембранные белки
С трудом поддаются выделению, многие вообще не выделяются без нарушения структуры. Белки в мембране отличаются большим разнообразием. Большинство белков в мембране находятся в виде клубка, 30% белков могут находится на поверхности мембраны в виде спирали. Существует несколько классификаций мембранных белков:
Функциональная классификация
ферментативные,
транспортные,
рецепторные,
каналообразующие,
воротные,
структурные.
Классификация по локализации по отношению к липидам.
интегральные,
периферические.
Интегральные белки погружены в мембрану или пронизывают ее насквозь. Периферические белки на поверхности мембраны и слабо связаны с ней – слабые взаимодействия. На поверхности интегральных белков имеется значительно меньше участков, несущих электрический заряд, чем на поверхности периферических белков.
Вандеркой и Капалди 1972 г. – все аминокислоты делятся на полярные, неполярные и промежуточные. Полярность а-к первой группы приняли за 1, полярность а-к второй группы – за 0, полярность а-к третьей группы – за ½. Изучили состав периферических и интегральных белков: 20 видов мембранных белков: средняя полярность всех белков равна 0,46; интегральные белки имеют полярность от 0,3 до 0,4; периферические белки имеют полярность от 0,41 до 0,53.
Углеводы мембран
В связанном виде не встречаются. В состав мембранных углеводов входят следующие сахара:
Д-галактоза,
Д-глюкоза,
ацетилглюкозамин,
ацетилгалактозамин,
Д-фруктоза,
Д-манноза,
Д-ксилоза.
Родопсин – гликопротеин оболочки сетчатки, состоит из углеводородной цепочки (4%), связанной с белками М=28000 Да. Гликопротеиды являются рецепторами для гормонов, медиаторов, пептидов и др. Большое кол-во гликопротеидов в вирусных оболочках (до 40% оболочки).
Вода
С ней связаны многие структурно-функциональные свойства мембран, а так же процессы стабилизации и формирования мембран. Вода входит в состав мембран и делится на свободную, связанную и захваченную. Связанная и свободная вода различается по подвижности молекул воды и растворяющей способности. Наименьшей подвижностью и растворяющей способностью обладает внутренняя связанная вода. Она присутствует в липидной зоне мембран в виде отдельных молекул. Основную часть связанной воды представляет вода гидратных оболочек. Эта вода окружает полярные группы белков и липидов, имеет min подвижность и практически не обладает свойствами растворителя. Свободная вода в порах и каналах. По ней могут перемещаться свободные ионы. Она является хорошим растворителем, подвижная и обладает всеми свойствами жидкой воды. Захваченная вода обладает изотопным движением, характерным для жидкой воды, является хорошим растворителем. Она встречается в центральной зоне мембран, между ее липидными слоями, но эта вода пространственно делится как с внеклеточной жидкостью, так и с цитоплазмой. У нее нет возможности свободно с ними обмениваться.
Струкрурная организация мембран
Плохо изучена, но внедряется электронная микроскопия, ЯМР, ЭПР.
Мембраны – 3х слойная структура с наружным и внутренним слоем, тонкие, темные до 2,5 нм, внутренний слой между ними светлый до 3,5 нм. Считается, что основой биомембран в большинстве случаев являются мембранные липиды. 1925 г. Грейбель и Гортер описали свойство фосфолипидов самопроизвольное образованием ими угла биомолекулярного слоя с замкнутой поверхностью в водной среде. Липиды образуют шаровидные образования.
Рисунок. В другой работе показано, что такие образования сохраняют устойчивость, если внешний d этой замкнутой поверхности не меннее 30 нм, так как чем меньше d, тем зазоры между головками липидов больше и вода просачивается внутрь замкнутого образования и нарушает стабильность. Стабильность бислоя определяется заряженными головками липидов.
Ассимметричность – 2ух слоев, они могут состоять из разным липидов.
Эритроцитарная мембрана: во внешнем слое много фосфатидилхолина и сфингомиелина, во внутреннем слое много фосфатидилэтаноламина и фосфатидилсерина. Во многих случаях неполярные хвосты содержат цепочки от 10 до 22 атомов С, между которыми могут быть насыщенные и ненасыщенные связи, это обуславливает ряд свойств мембран. Чем больше ненасыщенных связей, тем ниже t0 замерзания липидного бислоя. Внутренний слой бислоя нерыхлый, он содержит множество холестерина, он заполняет пространство между неполярными хвостами, влияет на t0 замерзания бислоя: чем больше холестерина, тем ниже t0 кристаллизации. Холестерин участвует в стабилизации мембран и будет влиять на проницаемость мембран, чем его больше, тем ниже проницаемость мембраны.
Мембранные липиды обладают динамическими свойствами:
способность липидной молекулы к латеральной диффузии, коэффициент латеральной диффузии равен 3,25*10–8 см/сек. Коэф отражает способность перемещения липидной молекулы вдоль мембраны,
вращательная диффузия, К=10–9 сек,
flip-flop переход, липидные молекулы пересекают мембрану, переходя из одного слоя в другой. К=10–3 сек средняя величина, показывающая число переходов – 1 переход в 1000 сек.
Организация мембранных белков
Большая часть мембранных белков находится в виде клубка (≥70%), основная часть может разворачиваться на поверхности липидного бислоя вследствие электростатического взаимодействия с липидными головками. В этом случае белки будут расположены на поверхности липидов в виде спирали.
Родоспин, М=28000 Да, форма сферы, d=4 нм, мелкая молекула.
Динамические свойства белков.
Латеральная диффузия. все значения для белков с М=100000, К=3*10–10 см/сек. Но белки могут объединяться в кластеры, которые мало подвижны.
Вращательная диффузия К=0,34 сек.
flip-flop переходы, К=10–4 сек – частота flip-flop перехода.
Модели биологических мембран
В 1935 г. модель Даниэля Доусона унитарная модель био мембран. Липидный бислой – структурная основа. Наружный и внутренний слои – глобулярные белки. Симметричная модель.
Модель Робертсона (середина 60х г). Мембрана представляет собой 3х слойную структуру, средний слой из липидов. Белковые молекулы развернуты на поверхности двойного липидного слоя вследствие электростатических взаимодействий заряженными головками фосфолипидов. Модель Робертсона ассимметрична, так как на наружной поверхности мембраны – гликопротеиды.
В группе моделей предполагается наличие белков матрицы. Модель Лючи (середина 60х г.) – белково-кристаллическая модель.
Модель _______________ (1970) сохраняется концепция липидного бислоя, однако этот слой прирастается участками симметрично расположенных белков, они жестко фиксированны пространственно за счет дальнодействующих белок-белковых свойств.
Модель Сенгера и Николсона. 60-70 г. Основа – липидный бислой, в который включены молекулы интегральных и периферических белков.
Жидкомозаичная модель. С ее помощью объясняется проницаемость мембран.
Мембранный транспорт
Активный: вещества переносятся через мембрану против концентрационного, электрического и других видов градиентов, на это тратится энергия клеточного метаболизма. Первичный активный транспорт и вторичный активный транспорт.
Пассивный: вещество без затрат энергии клеточного метаболизма переносится через мембрану в направлении градиента. В его основе диффузия и осмос.
Диффузия
определяется движением молекулярных частиц по направлению концентрационного градиента. Диффузия в физике рассматривается на примере простых моделей. Для полной диффузии необходимо несколько суток. Для био систем скорость диффузии не изменяется, но она осуществляется очень быстро. Процесс диффузии через мембрану изучают на примере:
Скорость диффузии будет определяться количеством вещества, диффундирующем в единицу времени.
Закон Фика.
dQs/dt=Ds*A*dCs/dx
dQs/dt – количесво вещества диффундирующее в единицу времени
Ds – коэффициент диффузии
А – площадь поверхности
dCs/dx – концентрационный градиент (изменение концентрации вещества с расстоянием)
Для скорости диффузии важной величиной является концентрационный градиент. Коэф диффузии зависит от природы и молекулярной массы растворенного вещества и растворителя. Из правого в левый движение хаотичное, но оно не велико. Будут наблюдаться однонаправленные потоки – количество растворенного вещества, пересекающих единицу площади поверхности молекулы за 1 секунду в данном направлении.
Iоднонапр потока = dQs/dt , I измеряется в моль/см2*сек.
Однонаправленный поток вещества в одном направлении не зависит от потока этого же вещества в противоположном направлении.
dQs/dt=P*(C1-C2),
для описания диффузии незаряженных молекул.
Р – проницаемость мембраны,
(C1-C2) – разность между концентрацией вещества 1 и 2.
[C]=моль/см3,
[P]=cм/с.
Скорость движения незаряженных молекул является линейной функцией концентрационного градиента. Р является функцией рассматриваемых мембран и диффунцирующего вещества.
Р=Дм*К/х,
Дм коэффициент диффузии вещества внутри мембраны (чем больше вязкость мембраны, тем больше диффузия молекул, тем ниже эта величина). К- коэффициент распределения. х – величина толщины мембраны. Коэффициент проницаемости от 10–12 до 10–2 см/сек эритроцитарный.
Под действием антидиуретического гормона проницаемость мембраны может возрастать в 10 раз.
Осмос
1748 г. – открытие осмоса. Офицально считается, что открыл Жан-Антуан Молле. Особые свойства мочевого пузыря лягушки. установил, что эта мембрана обладает особым свойством: если по одну сторону чистая вода, по другую растворенные вещества (растворы сахаров). В этих условиях вода начинает активно проникать через мембрану мочевого пузыря в раствор.
Осмос заключается в переходе молекул воды через мембрану по направлениям ее концентрационных градиентов. Наступает равновесие (динамическое) определяется фактором осмотического давления (направление слева направо).
Гидростатическое давление раствора в правом отсеке, когда эти два давления уравновесили друг друга, то мы получим равновесие. Вывод: для того, чтобы измерить осмотическое давление раствора нужно измерить гидростатическое давление во втором отсеке.
В 1877 г. Пфейффер определил количественный показатель осмоса с помощью осмометра (имеет полупроницаемую мембрану – из осадочного ферроцианида Сu). Пфейффер сделал заключение – осмотическое давление пропорционально концентрации растворенного вещества.
Вант-Гофер: в термодинамическом отношении молекулы воды ведут себя подобно молекулам газа.
π=RTS или π=RTη/V,
π – осмотическое давление,
RTη – количество молей вещества,
R – газовая постоянная,
Т – абсолютная температура,
С – концентрация.
Это выражение справедливо лишь для разбавленных растворов.
Осмотичность:
два раствора, в которых создается одинаковое осмотическое давление по обе стороны мембраны проницаемой только для воды называются изоосмотическими, растворы содержат в единице объема одинаковое число растворенных молекул. Если один из растворов имеет осмотическое давление по отношению к другому, то первый раствор называется гиперосмотически, второй – гипоосмотическим.
Тоничность:
определяется по реакции клеток и тканей на их погружение в раствор; если при погружении в раствор ткань не набухает, не сморщивается, такой раствор называют изотоническим по отношению к ткани. Если при погружении ткань набухает – раствор гипотонический, если ткань сморщивается – раствор гипертонический.
Транспорт ионов
Необходимо учитывать и влияние электрических сил.
На заряженные частицы (органические и неорганические ионы) действуют 2 силы, определяющие их диффузию через мембрану: концентрационный градиент и электрическая сила (определяется разностью потенциалов). Совокупность этих двух сил составляет электрохимический потенциал.
Существует разность потенциалов, уравновешивающая действующий на данный ион концентрационный градиент и предотвращающая трансмембранный перенос данного иона. В этой ситуации будет существовать некоторое состояние равновесия – электрохимическое равновесие, а соответствующие потенциалы мембраны будут называться равновесными потенциалами. Например, на мембране много К+, идет отток К+. Если зарядить внутреннюю поверхность мембраны до –97 мВ, для Na+ равновесный потенциал ≈ +55 мВ.
Диффузия заряженных частиц может происходить против концентрационного градиента, если электрический градиент будет направлен противоположно концентрационному и будет превышать его действие.
Доннановское равновесие
Фредерик Доннан – физико-химик, 1911 г.
Если налить в сосуд с полупроницаемоей перегородкой воды, то в 1 и 2 будет вода. Доннан добавил в первый отсек соль KCl. По прошествии определенного времени концентрации различных ионов в двух отсеках стали равны. Доннан взял соль с органическими ионами, которые не проходят через мембрану. Через некоторое время ионы K+ и Cl– начинают диффунцировать. Наступает ситуация при которой в первом отсеке [K+] больше, чем во втором, в первом отсеке [Cl–] меньше, чем во втором.
Вывод: анион, не проходящий через мембрану оказывает на распределение анионов и катионов, свободно проходящих через мембрану между отсеками.
Такая же ситуация наблюдается и в клетках и в биосистемах. Установленное Доннаном равновесие обусловлено несколькими фактами:
Оба отсека по отдельности должны быть электронейтральными, то есть в каждом отсеке число "+" ионов должно быть равно числу "–" ионов.
Диффундирующие ионы (K+ и Cl–) пересекают мембрану парами, при этом сохраняется электронейтральность отсеков. Вероятность пересечения мембраны этими ионами определятется произведением их концентраций [K+]*[Cl–].
В равновесии скорость диффузии KCl в одном направлении равна скорости диффузии KCl в противоположном направлении. Поэтому [K+]*[Cl–] должно быть одинаковым для обоих отсеков.
Математическое выражение Доннановского равновесия:
[K+]2/[K+]1=([A–]1+[Cl–]1)/[Cl–]2.
Механизмы пассивного транспорта через мембраны
Пассивный транспорт осуществляется главным образом тремя способами:
Вещества, находящиеся в водной фазе по одну сторону мембраны, растворяются в липидно-белковом слое мембраны, пересекают его и вновь переходят в водную фазу с противоположной стороны мембраны.
Вещества, которые перемещаются через поры или каналы мембраны, заполненные водой.
Молекулы транспортируемого вещества соединяются с молекулой переносчиком, встроенным в мембрану и переносчик опосредует или облегчает транспорт – этот транспорт называют облегченной или опосредованной диффузией. Молекулы переносчика всегда жирорастворимы, они ускоряют транспорт веществ по их концентрационному или электрохимическому градиенту.
Первый механизм:
Простой транспорт. Он осуществляется под влиянием теплового движения частиц. Для того, чтобы попасть из водной фазы в липидную, молекула должна разорвать все свои водородные связи с водой, на это затрачивается энергия 5 ккал/моль водородных связей. Чем меньше молекула образует водородных связей, тем больше ее шансы проникнуть через мембрану. Этот вид транспорта только для незаряженных молекул. На подвижность молекулы внутри мембраны будет влиять молекулярная масса и форма молекулы. Но самый главный фактор – это коэффициент распределения. Он определяется экспериментально: берется пробирка, соедржащая равные объемы (количества) воды и оливкового масла, затем в нее добавляется исследуемое вещество. Пробирку хорошенько встряхивают, чтобы смесь распределилась по всему объему. Затем определяют концентрацию этого вещества в воде и в масле.
Коэф. распр. К = конц в-ва в липидной фазе / конц в-ва в водной фазе.
1937 г. Колландер Р. провел очень большие исследования на гигантских клетках пресноводных водорослей, которые были посвящены изучению зависимости коэф. распр. и проницаемости мембраны для веществ существует некая генеральная зависимость.
Распределение точек для различных веществ. Но были исключения, например H2O, CO2 и другие мелкие незаряженные молекулы – наблюдаются большие колебания К и проницаемости. Гексанол (1 ОН) и монитол (6 ОН) одинаковы по элементарному составу. Это приводит к тому, что –ОН группы образуют водородные связи с водой, поэтому снижается растворимость вещества в липидах, это сказывается на К. Наличие только одной –ОН группы снижает К в 40 раз.
Поэтому гексанол диффундирует гораздо быстрее, чем монитол.
В отношении воды было сделано предположение: она дополнительно диффундирует через поры мембраны. Это было доказано экспериментально: если брать синтетическую мембрану, но состоящую только из липидов, вода проходит через нее еще одни механизм, связанный с динамическими свойствами липидов. Так как во время этих динамических движений образуются дефекты и очень подвижные молекулы воды успевают протикнуть через них через мембрану.
Кинетика такого транспорта характеризует графическую зависимость скорости поступления через мембрану от концентрации вещества вне клетки. Эта прямая отражает кинетику без насыщения (то есть концентрация вещества может возрастать до бесконечености). Такая кинетика отличает простую диффузию от двух других механизмов пассивного транспорта.
Второй механизм:
Диффузия через мембранные каналы. Основная масса каналов специфична (пропускает только один вид ионов), другие или не- или частично специфичны, причем каналы заполнены водой. Это доказано экспериментрально в наблюдениях на искусственном липидном бислое. Если на его поверхность поместить электролит, то прохождения ионов нет, если добавить каналообразующие белки, то возникает электрический ток. Каналообразующие белки выделяют из природного сырья, причем они самостоятельно встраиваются в мембрану. В настоящее время разработаны методы выделения каналообразующих белков. Нестатин – противогрибковый антибиотик, его молекулы представляют собой стержневидные образования, которые могут встраиваться, как в естественные, так и в искусственные мембраны.
Через такие поры могут проходить отрицательные ионы (Cl–, молекулы воды, мочевина, мелкие незаряженные частицы, +заряженные частицы не проходят). На такой модели изучали этот вид транспорта. В области высокой концентрации наблюдается явление насыщения, так как пропускная способность ионноых каналов ограничена. Но в биосистемах явления насыщения не встречается.
Третий механизм:
Облегченная диффузия.
Это говорит, что скорость увеличивается только при относительно низких концентрациях. Это кинетика насыщения.
Причины кинетики насыщения:
Связывание проникающей молекулы с определенным участком внутри канала или вблизи него.
Основная причина – транспорт вещества через мембрану с помощью молекулы-переносчика:
а) количество молекул-переносчиков ограничено,
б) скорость из реагирования с переносимым веществом так же лимитирована.
Скорость облегченной диффузии достигает max, когда все молекулы переносчика будут заняты транспортируемым веществом.
Теория облегченной диффузии напоминает теорию субстрат-связывающего комплекса. Данный вид транспорта можно ингибировать с помощью химических аналогов транспортируемого вещества.
Механизмы первично активного транспорта
Энергия клеточного механизма концентрируется в виде АТФ. Существуют специальные мембранные насосы, их совокупность – первично активный транспорт. Источник энергии – клеточный метаболизм, если отключить источник энергии, то ионы расположатся равномерно, относительно мембраны. Концентрационный градиент направлен внутрь клетки, ионы Na пассивно поступают внутрь клетки. Но концентрационный градиент постоянен, так как ему противостоят Na насосы.
Основные особенности первично активного транспорта:
Осуществляется против концентрационного градиента.
Система первичного транспорта в высшей степени специфична (Na система не перекачивает другие ионы).
Для его обеспечения необходима АТФ или другие источники энергии (метаболические яды блокируют насос).
Обменивает один вид ионов на другой (К-Na насос).
Многие виды ионных насосов выполняют электрическую работу, перенося заряды через мембрану (реогенный насос – это насос, при работе которого создается электрический ток).
Активный транспорт с помощью ионных насосов избирательно подавляется блокирующими агентами. (Существуют специфические вещества, которые блокируют данный насос, например, убаин – сердечный гликозид. Это вещество конкурентно блокирует участки, связывающие ионы К+.)
Энергия, необходимая для первично активного транспорта, высвобождается при гидролизе АТФ ферментами, расположенными в мембране. Активность ферментов зависит от концентрации ионов.
Современная гипотеза первично активного транспорта
K-Na-АТФаза – молекула из двух субъединиц, имеющих внутренние полости: -большая субъединица (полипептид), -малая субъединица (гликопротеид). обладает высоким сродством к Na +, - к К+. Полость -субъединицы заполняется 3 ионами Na+, полость -субъединицы заполняется 2 ионами К+. Потом у -субъединицы сродство к Na+ падает, а у -субъединицы сродство к К+ возрастает.
За счет флуктуации происходит пространственное совмещение полостей субъединиц и обмен ионами. В конце цикла полости открываются, и ионы их покидают.
Другая гипотеза. В начале происходит заполнение полостей описанным выше способом, затем поворот K-Na-АТФазы на 1800. После чего ионы покидают полости, а K-Na-АТФаза опять поворачивается на 1800. Если молеула постоянно переворачивается, то это должно привести к перестройке молекулярного слоя – спорный момент.
Механизм вторично активного транспорта
заключается в переносе веществ через мембрану против концентрационного градиента, обеспечиваемом энергией, которая высвобождается при переносе другого вещества по градиенту. То, что транспортируется по градиенту, называется синпортом, или ко-транспорт. Пример, транспорт а-к или сахаров через био мембраны.
Транспорт в клетки аланина.
В присутствии внеклеточных ионов Na+ транспорт аланина в клетки осуществляется до тех пор, пока внутриклеточная концентрация Na+ будет в 7-10 раз больше внеклеточной. Если во внеклеточной среде Na+ отсутствует, то концентрация аланина внутри клетки не отличается от внеклеточной.
2 рисунка. max скорость транспорта в двух случаях одинакова. Внеклеточный Na+ оказывает непосредственное влияние на транспорт аланина (различный наклон графиков). Если повысить внутриклеточную концентрацию Na+, то аланин из клетки будет выходить во внеклеточную среду. Вторично активный транспорт не зависит от концентрации Na+ вне клетки, а зависит от концентрации градиента ионов Na+. Градиент Na+ является движущей силой, промежуточной стадией в процессе использования энергии (в системе вторично активного транспорта).
Системы антипорта, или контр-транспорта – это система вторично активного транспорта, функциорующая на основе переносчика обменника, обеспечивающего выведение из клетки транспортирующего вещества против его концентрационного градиента в обмен на сопряженный, пассивно поступающий в клетки поток ионов Na+. Движущей силой является потенциальная энергия концентрационного градиента ионов Na+.
Примеры:
Транспорт Ca2+ в обмена на Na+, осуществляется во многих типах клеток. Уровень концентрации внутриклеточного Ca2+ 10–9 моля, внеклеточной – 10–6 моля. Мышечное сокращение, выделение нейромедиаторов синапсами регулируется Са2+-зависимыми К+-каналами. Механизм: и ионы Nа+ и ионы Са2+ имеют один и тот же переносчик, у внутренней поверхности мембраны, обладающей высоким сродством к Са2+, у наружной – к Nа+. Са2+-насос удаляет Са2+ из клетки.
Антипортная система клеток проксимальных отделов нефрона, обменивающая Nа+ на Н+. Из мочи к клетки проксимальных отделов нефрона выделяется Nа+, взамен выводится Н+. Система не совершает электрическую работу, поэтому не надо тратить энергию. K-Na-насос сохраняет Nа+ в организме.
Визикулярный транспорт
происходит путем эндо- и экзоцитоза. Это вид транспорта, при котором вещества перекачиваются внутрь клетки или из нее внутри маленьких пузырьков или визикул. Жидкие вещества – пиноцитоз, твердые вещества – фагоцитоз. Когда переносятся гормоны или медиаторы, то вначале они взаимодействуют с мембранными рецепторами. Рецепторы обладают способностью к латеральной диффузии, при этом образование комплекса рецептора с лигандом вызывает перемещение этого комплекса в углубление мембраны.
Образуется окаймленная ямка. Внутренняя поверхность покрыта особым белком – клатрином, он связывает занятую лигандом молекулу рецептора, затем этот белок участвует в отшнуровывании визикулы от поверхности мембраны. Визикулы разрушаются, но некоторые проходят насквозь, и тогда вещества высвобождаются с другой стороны. Когда визикула разрушается внутри клетки – эндоцитоз, вне клетки – экзоцитоз. Мембранный материал вновь включается в клетку круговорот.
Потенциал покоя
это разница потенциалов между цитоплазмой и внеклеточной средой, существующая в каждой живой клетке, находящейся в состоянии покоя. Внутриклеточная среда заряжена отрицательно. Величина ПП может быть различной, зависит от состояния клетки от –15 до –90 мВ у большинства клеток.
Для того, чтобы измерить величину ПП используется микроэлектродная техника. Используется специальный вид электродов, отличающийся намного меньшим диаметром кончика (доли мкм, или 1 мкм). Бывают стеклянные и металлические, по форме напоминают копье, необходим раствор электролита для хорошего проведения электрического тока.
Основные теории ПП:
В 1848 г. Дюбуа-Реймон "теория электромоторных молекул" (теория заряженных диполей). Дюбуа-Реймон предположил, что на мембране находятся диполи, ориентированные отрицательным зарядом внутрь. При возбуждении диполи поворачиваются на 1800, что приводит к положительному заряду внутри клетки. Разность потенциалов в этой теории является предшествующей.
В 60-е годы XIX в. – альтернативная теория Германа. В состоянии покоя мембрана клетки не заряжена, и ПП отсутствует. Однако при повреждении, в поврежденном участке появляется избыток отрицательного заряда, в силу наличия кислых продуктов. Поэтому между поврежденными и неповреждеными участками возникает электрический ток. Теория Германа исключала существование разности потенциалов на мембране.
Теория полупроницаемой мембраны Берштейна. 1906 г. Положения:
мембрана обладает свойством полупроницаемости (в специальных экспериментах в группе Пфейффера показали: при пропускании электрического тока – поляризация мембраны и появление концентрационной электро-двигательной силы.
наличие концентрационных градиентов на биологической мембране. В исходном состоянии К+, Сl–, Na+ и другие распределены различно на мембране. Берштейн обратил внимание на К+-концентрационный градиент по направлению из клетки наружу.
Существуют механические насосы. Перемещение из клетки через мембрану осуществляется по градиенту; но выход не бесконечен, как только К+ выйдет из клетки, образуются силы, противодействующие этому выходу. 1. Первый положительный заряд на мембране препятствует выходу остальных (электростатическое отталкивание). 2. Крупные молекулы, которые не могут проходить через мембрану, мембраны их не пропускают, они не будут пропускать К+ мембранный слой ионов К+ снаружи, слой анионов изнутри. При повреждении мембраны анионы выходят наружу и создается электрический ток.
Еm = RT/F * ln([K+]ant/[K+]in)
Еm – ПП, F- число Фарадея.
Эксперимент: кнаружи поверхности мембраны облицеров. соли К+ выход ионов К+ из клетки затруднен величина ПП?
Результат: ампликация солей К+ к наружной поверхности мембраны приводит к снижению величины ПП, степень снижения оказалась пропорциональной концентрации К+ в облицеров. растворе.
Вывод: К+ имеет основное значение в генерации ПП.
Если удалить Na+ или изменить его концентрацию во внеклеточной жидкости, это не толко не снизит величину ПП, но даже приведет к небольшой дополнительной поляризации мембраны Na+ не играет существенной роли в генерации ПП.
Прямые определения концентрации К+ в клетке и окружающей среде показали хорошее соотношение с теоретически рассчитанными значениями ПП. После Бернштейна данные подтверждались.
Джерард и Фурузава, 1930 г. Работали на нервах краба в условиях гипоксии и апоксии (полное отсутствие О2). ПП прогрессивно снижался и, наконец, исчез в нормальном целостном участке нерва.
Вывод: энергия, необходимая для генерации ПП берется из окислительных процессов.
Современная мембранная теория
Ходжкин и Хаксли разработали в 30х годах ХХ в., используя микроэлектродную технику на гигантских аксонах кальмара. ПП –50 мВ. При возбуждении генерации ПД амплитуда до 100 мВ.
С позиции теории Берштейна. При возбужедении растет проницаемость мембраны для всех ионов. При этом происходит перераспределение этих ионов в сторону выравнивания концентрации внутри и вне клетки, поэтому ПД = ПП ( –50 мВ) кризис мембранной теории Берштейна.
Основные положения современной мембранной теории
Клеточные мембраны обладают избирательной проницаемостью не только к ионам состоянии К+, но и к Na+ и к другим.
Эти виды ионной проницаемости обнаруживают самостоятельную изменчивость в зависимости от функционального состояния клетки.
В мембране диэлектриком явлется липидная фаза (конденсатор), чтобы зарядить конденсатор до –75 мВ на 1 мм2 должно находиться 5000 пар ионов. В генерации ПП участвует К+, концентрация внутри клетки в 20 раз выше концентрационный градиент для внутрь клетки (так как во внеклеточной среде концентрация ионов Na+ в 5-15 раз больше, концентрация Сl– вне клетки в 20-100 раз больше.
Чем больше проницаемость мембраны для иона, тем больше в клетку вносится данного иона.
Р К+ : Р Na+ : Р Сl– = 1 : 0,04 : 0,045
Уравнение Гольдмана:
Em = RT/F * ln (PК+*[К+]out+ PNa+*[Na+]out+ PCl–*[Cl–]out)/(PК+*[К+]in+ PNa+*[Na+]in+ PCl–*[Cl–]in)
Потенцил Действия
Объясняется поворотом диполя на 1800.
Теория альтерации Германа. При возбуждении возникает избыток кислых продуктов, которые несут отрицательны заряд, что приводит к разности потенциалов между возбужденным и невозбужденым учаском.
Мембранная теория Берштейна. В возбужденном участке мембраны резко увеличивается проницаемость для всех ионов, концентрации ионов смешиваются и участок становится электронейтральным.
Ходжкин и Хаксли. Рост проницаемости мембраны для ионов в месте воздействия. При возбуждении электропроницаемость мембраны увеличивается примерно в 500 раз. Max увеличивается проницаемость мембраны для Na+ (отсюда Na-теория ПД). Na+ свободно проходит внуть клетки. При возбужедении электро-химическое равновесие определяется потенциалом Na+. Равновесный потенциал для К+ = –97 мВ, для Na+ = +50 мВ. При возбужедении мембрана перезаряжается. Положение обратной активации и инактивации Na+-каналов, Na+-канал может активироваться (открываться) при определенных значениях потенциала. Причина активации Na+-каналов – деполяризация мембраны, чем больше деполяризация, тем больше проницаемость мембраны для Na+. Зависимость близка к линейной в подкор уровне; как только мембрана достигнет критического уровня деполяризации – зависимость нелинейная, лавинообразный вход Na+ в клетку.
1). Для объяснения реполяризации используется положение об инактивации Na+-каналов. При приближении потенциала мембраны к равновесному для Na+, Na+-каналы инактивируются и посупление Na в клетку прекращается. К графику: в основе регенеративный процесс (сам себя поддерживающий), развивающийся по принципу обратной связи.
2). Рост К+ проницаемости мембраны. Не столь значителен, как для Na+ ( в 5-15 и 500 раз соответственно). Проницаемость для К+ развивается медленнее, чем для Na+. Ионы К+ в этой ситуации будут выходить наружу и выносить заряд.
3). Механизм активного транспорта, представленный K-Na-насосом. 3 Na+ внутрь и 2 К+ наружу.
Эксперименты Ходжкина и Хаксли.
Гигантский аксон кальмара. Из внеклеточной среды были удалены 2/3 Na+. При этом амплитуда ПД снизилась на 50%. Замена внутриклеточного Na+ на другие ионы приводит к некоторому росту ПД. Замена ½ внутриклеточного К+ на Na+ приводит к значительному снижению ПД.
Метод фиксации потенциала
метод Петч-Клемпинга. С его помощью можно зафиксировать на длительное время значение мембранного потенциала на любом желаемом уровне. Это делается с помощью внешнего генератора напряжения
Суммарные мембранные токи при ПД
Подпороговая область:
Слабое изменение мембранного потенциала, суммарный ионный ток направлен от клетки наружу, так как поток К+, выходящий из клетки, уже усиливается из-за удаления мембранного потенциала от равновесного потенциала для К+. Входящий ток Na+ еще слаб, так как рост Na+-проницаемости пока невелик. Однако с развитием деполяризации Na-ый поток постепенно нарастает.
Критический уровень деполяризации:
В этот момент суммарный ионный ток через мембрану равен нулю, так как встречные токи ионов Na+ и К+ уравновешивают друг друга. Даже небольшая дальнейшая деполяризация приводит к росту входа Na+-тока в сотни раз.
Во время фазы деполяризации резко увеличивается Na+-проницаемость и суммарный мембранный ток, направленный внутрь клетки. Выходящий К+-ток растет медленнее и становится заметным только к моменту пика потенциала.
Фаза реполяризации:
В момент пика потенциала большинство Na+-каналов инактивированны, а К+-ток max. Поэтому суммарный мембранный ток – выходящий.
Кальциевая теория активации и инактивации Na+-каналов
В состоянии покоя у наружного отверстия Na+-канала находится Са2+, который электростатически тормозит проникновение Na+ в канал. При возбуждении наружная поверхность мембраны заряжена отрицательно, при этом Са2+ уходят со своих мест, вход открывается и Na+ входит в клетки.
Инактивация: по ходу деполяризации узкие Na+-каналы могут закупориваться Na+. Во многих каналах есть воротные белки (могут менять свое местоположение под влиянием изменения потенциала). В состоянии покоя активационный белок закрыт, а инактивационный открыт. При возбуждении открывается активационный белок в момент закрывания инактивационного белка. В конце реполяризации белки так же закрываются и потом открываются (исходное состояние).
Передача возбуждения по нервным волокнам
В начале 30х годов ХХ в. Хилл. 1932 г. "Химическая волна проведения в нервах". Хилл использовал разные нервы, но преимущественно краба. Даже в состоянии покоя в единицу времени вырабатывается некоторое количество тепла. Это тепло было названо теплопродукция покоя. Когда в нервном волокне возбуждение – теплопродукция возбуждения (ТВ), она делится на 2 фазы:
Начальная ТВ, которая составляет 2-3% от всей ТВ и приходится непосредственно на период возбуждения.
Задержанная ТВ 97% всей ТВ. Если подать серийный импульс на нерв краба, то задержанную ТВ можно зафиксировать в течение 25-30 минут. Возбуждения в тканях уже нет, но ТВ имеет место.
Утечка тепла при работе Na.
Хилл разрабтал чувствительную теплоэлектрическую методику, которая позволяла фиксировать теплообразование в течение 20 мс. Эксперименты при О0 С. Начальную фазу теплопродукции делили на 2 периода: позитивная и негативная начальная теплопродукция. При О0 С для нерва краба позитив в начальные 20 мс = 14 мк кал. В течение последующих 150 мс 85% тепла поглощается нервной тканью обратно (12 мк кал).
Позитивная начальная теплопродукция: причина: химические процессы, обуславливающие изменение проницаемости мембраны. При возбуждении в клетку поступает Na+ и смешивается с К+ и наоборот. Должно образовываться тепло. Это тепло покрывает до 50% позитивной начальной теплопродукции.
Негативная начальная теплопродукция: химические реакции в этот период могут быть эндотермическими. Негативная теплопродукция не является обязательной.
Проведение возбуждения
В 1885 г. Герман предложил теорию малых токов. Осуществляется последовательно между участками волокна. В участке, соседнем с возбужденным будет наблюдаться выход электрического тока.
Кабельная теория нервного волокна: нервное волокно внутри содержит проводящую среду, оболочка невного волокна имеет слой, который плохо проводит возбуждение. Нервное волокно омывается внеклеточной жидкостью, которая проводит электрический ток.
Эквивалентная электрическая схема нервного волокна
В состоянии покоя внутриклеточная среда имеет избыточный отрицательный заряд. Сила тока меняется с расстоянием от возбужденного сегмента, декремента.
Факторы, определяющие скорость распространения возбуждения по нервному волокну
Пространственная константа определяет величину декремента деполяризации, - пространственная константа.
Коэффициент надежности, соотношение между амплитудой ПД, критической энергией и ПП. S=ПД/(Екр–ПП), ПД=120мВ, ПП=–70мВ, Екр=–55мВ S=8. Чем больше S, тем быстрее проведение.
Временная константа мембр. При возбуждении мембраны меняется заряд. Длительность перезарядки мембраны. мембр=Rm*Cm. Чем больше мембр, тем ниже С. Vраспр=S*/мембр.
Механизм распространения возбуждения
Возбуждение охватывает последовательно все отделы нервного волокна. R наруж влияет на скорость распространения возбуждения. В экспериментрах Ходжкина изменили внеклеточную среду на масло, которое имеет большее сопротивление, объем снизился на 30-50%. Эксперимент: нерв помещается на параллельные пластинки из серебра, замыкают с помощью ртутной ванночки, объем проведеним растет на 16-30%. Была подтверждена теория местных токов для безмякотных волокон. В мякотных нерных волокнах механизм проведения другой. Миелин имеет рост сопротивления и снижение емкости, миелиновая оболочка прерывается перехватами Ранвье – сальтаторное проведение. R на 1 см2 поверхности в перехвате Ранвье = 10-20 Ом, в миелиновой оболочке = 0,003-0,005 Ом. Петли тока в миелиновых нервных волокнах выходят через невозбужденый перехват Ранвье, находящийся спереди от возбужденного . Эксперименты Тасаки.
Электроды стоят на миелине, два выходящих тока (это токи, выходящие из последующего и предыдущего перехвата Ранвье. Входящий ток не регистрируется.
Средний электрод на перехвате. Появляется входящий ток.

Нравится материал? Поддержи автора!
Ещё документы из категории биология:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ