Методика группировки показателей

Выборка банков

Таблица 1 – Список 30 крупнейших банков России по размеру капитала, млн. руб.

Ранг

Название банка

Город

Чистые активы

Прибыль

Внешторгбанк

Москва

25286

1962

ОНЭКСИМбанк

Москва

19221

266

Инкомбанк

Москва

17275

744

Империал

Москва

6649

429

Международный московский банк

Москва

7609

290

Международный промышленный банк

Москва

4887

Российский кредит

Москва

12278

367

МЕНАТЕП

Москва

11058

146

Промстройбанк России

Москва

5651

239

Уникомбанк

Москва

3743

Возрождение

Москва

4079

158

Московский деловой мир

Москва

1951

340

Нефтехимбанк

Москва

2568

Ланта-банк

Москва

630

ИнтерТЭКбанк

Москва

1295

Гута-банк

Москва

5636

Совфинтрейд

Москва

1356

215

Совиндбанк

Москва

811

301

Русский банк имущественной опеки

Москва

425

Чейз Манхеттен Банк Интернэшил

Москва

2317

335

Еврофинанс

Москва

1283

Омскпромстройбанк

Омск

650

Запсибкомбанк

Тюмень

1137

133

Диалог-Банк

Москва

1012

127

Кредит Свисс АО

Москва

2869

118

МАПО-Банк

Москва

1237

Росэксимбанк

Москва

339

Уральский банк реконструкции и развития

Екатеринбург

513

115

Уралтрансбанк

Екатеринбург

622

143

Пробизнесбанк

Москва

1486

Способ отбора банков – механический. Я выбрал каждый второй банк.

1 Анализ выборочной совокупности

а) Количество групп определяем по формуле Стерджесса:

n = 1+3,322 lg N

где: n – число групп;

N – число единиц совокупности.

n=1+3,322 lg 30=5,906997≈6

Величина интервала определяется по формуле:

h = (X_max – X_min₎/n

где: X_max– максимальное значение группировочного признака;

X_min – минимальное значение группировочного признака.

h₁=(25286–425)/6 = 4143,5 млн. руб.

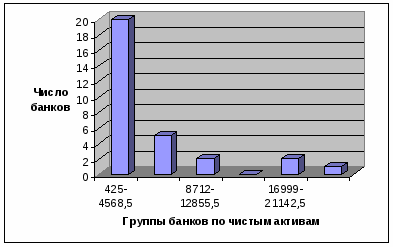
Таблица 2 – Группировка банков по чистым активам, млн. руб.

№ группы

Группы банков по чистым активам

Число банков

425–4568,5

4568,5–8712

8712–12855,5

12855,5–16999

16999–21142,5

21142,5–25286

Итого

h₂= (1962–5)/6=326,2 млн. руб.

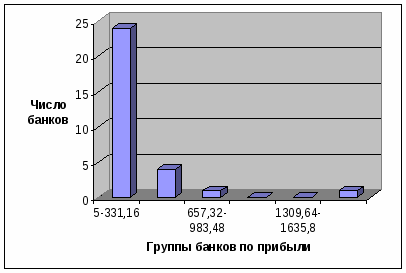
Таблица 3 – Группировка банков по прибыли, млн. руб.

№ группы

Группы банков по прибыли

Число банков

5–331,16

331,16–657,32

657,32–983,48

983,48–1309,64

1309,64–1635,8

1635,8–1962

Итого

б) Графики по данным полученных рядов:

Рисунок 1 – Группировка банков по чистым активам, млн. руб.

Рисунок 2 – Группировка банков по прибыли, млн. руб.

в) Средняя арифметическая взвешенная находится по формуле:

x = ∑ x_i * f_i/ ∑ f_i

Таблица 4 – Таблица для расчета средней арифметической по чистым активам

№ группы

Группы банков по чистым активам

Число банков, f

Середина интервала, X _i

X*f

425–4568,5

2496,75

49935

4568,5–8712

6640,25

33201,25

8712–12855,5

10783,75

21567,5

12855,5–16999

14927,25

16999–21142,5

19070,75

38141,5

21142,5–25286

23214,25

Итого

166059,5

х=166059,5/30=5535,3 млн. руб.

Таблица 5 – Таблица для расчета средней арифметической по прибыли

№ группы

Группы банков по прибыли

Число банков, f

Середина интервала, X _i

X* f

5–331,16

168,08

4033,92

331,16–657,32

494,24

1976,96

657,32–983,48

820,4

983,48–1309,64

1146,56

1309,64–1635,8

1472,72

1635,8–1962

1798,9

Итого

8630,18

х=8630,18/30=287,7 млн. руб.

Мода находится по формуле:

Мо = Хо + К*(F_MO – F_MO_-1/ (F_MO – F_MO_-1)+(F_MO – F_MO₊₁₎)

где: Хо – нижняя (начальная) граница модального интервала;

К – величина интервала;

F_MO- частота модального интервала;

F_MO_-1 – частота интервала, предшествующего модальному;

F_MO₊₁-частота интервала, следующего за модальным интервалом.

Находим модальный интервал по наибольшей частоте f₁. Наибольшая частота равна 20. Модальный интервал – [425–4568,5]. Хо = 425, К=4143,5

Мо ₁ = 425 + 4143,5*(20–0/(20–0)+(20–5))= 2604,04 млн. руб.

Вывод: наиболее часто встречается банк с размером чистых активов 2604,04 млн. руб.

f₂=24. Модальный интервал – [5–331,16]. Хо = 5, К=326,2

Мо ₂ = 5 + 326,2*(24–0/(24–0)+(24–4))= 178,8 млн. руб.

Вывод: наиболее часто встречается банк с размером прибыли 178,8 млн. руб.

Для определения медианы рассчитывают ее порядковый номер (N_Me)

N_Me = (n+1)/2

N_Me = (30+1)/2 = 15,5

Рассчитываем медиану (Ме) по формуле:

Ме = Хо + К*(( f / 2 – S_Me_-1) / f_Me)

где: Хо – нижняя граница медианного интервала;

К – величина интервала;

f = n – число единиц совокупности;

S_Me_-1– накопленная частота, предшествующая медианному интервалу;

f_Me– медианная частота.

Ме₁ = 425 + 4143,5*((30/2 – 0)/20) = 3426,4 млн. руб.

То есть 15 банков имеет чистые активы более 3426,4 млн. руб. и 15 – менее 3426,4 млн. руб.

Ме₂ = 5 + 326,2*((30/2 – 0)/24) = 207 млн. руб.

То есть 15 банков имеет прибыль более 207 млн. руб. и 15 – менее 207 млн. руб.

Абсолютные показатели вариации

Размах вариации – это разность между максимальным и минимальным значением статистической совокупности. Находится по формуле:

R=X_max – X_min

где: X_max- максимальное значение признака;

X_min- минимальное значение признака.

R₁= 25286–425 = 24861 млн. руб.

Разница между банком с максимальным размером чистых активов и банком с минимальным размером чистых активов равна 24861 млн. руб.

R₂=1962–5 = 1957 млн. руб.

Разница между банком с максимальным размером прибыли и банком с минимальным размером прибыли равна 1957 млн. руб.

Среднее линейное отклонение – это средняя величина из отклонений значений признака от их средней. Находится по формуле:

d =  |X_i – X| *f_i/  f_i

где X_i- значение признака;

Х – среднее значение признака;

f – частота.

Таблица 6 – Расчет среднего линейного отклонения по чистым активам

№ группы

Группы банков по чистым активам

Число банков, f

Середина интервала, X _i

|X _i – Х|

|X _i – Х|*f

425–4568,5

2496,75

-3038,55

-60771

4568,5–8712

6640,25

1104,95

5524,75

8712–12855,5

10783,75

5248,45

10496,9

12855,5–16999

14927,25

9391,95

16999–21142,5

19070,75

13535,45

27070,9

21142,5–25286

23214,25

17678,95

Итого

0,5

d = 0,5/30 = 0,02 млн. руб.

Средняя величина из отклонений размера чистых активов от их средней составляет 0,02 млн. руб.

Таблица 7 – Расчет среднего линейного отклонения по прибыли

№ группы

Группы банков по прибыли

Число банков, f

Середина интервала, X _i

|X _i – Х|

|X _i – Х|*f

5–331,16

168,08

-119,62

-2870,88

331,16–657,32

494,24

206,54

826,16

657,32–983,48

820,4

532,7

983,48–1309,64

1146,56

858,86

1309,64–1635,8

1472,72

1185,02

1635,8–1962

1798,9

1511,2

Итого

-0,82

d = -0,82/30 = -0,03 млн. руб.

Средняя величина из отклонений размера прибыли от их средней составляет -0,03 млн. руб.

Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины. Находится по формуле:

 ²=  (X_i – X)²*f_i/  f_i

Таблица 8 – Расчет дисперсии по чистым активам

Группы банков по чистым активам

Число банков, f

Середина интервала, X _i

X _i – Х

(X _i – Х)²

(X _i – Х)² *f

425–4568,5

2496,75

-3038,55

9232786,1

184655722

4568,5–8712

6640,25

1104,95

1220914,5

6104572,5

8712–12855,5

10783,75

5248,45

27546227,4

55092454,8

12855,5–16999

14927,25

9391,95

88208724,8

16999–21142,5

19070,75

13535,45

183208406,7

366416813,4

21142,5–25286

23214,25

17678,95

312545273,1

Итого

924814835,8

 ²=924814835,8/30=30827161,2 млн. руб.

Таблица 9 – Расчет дисперсии по прибыли

Группы банков по прибыли

Число банков, f

Середина интервала, X _i

X _i – Х

(X _i – Х)²

(X _i – Х)² *f

5–331,16

168,08

-119,62

14308,9

343414,7

331,16–657,32

494,24

206,54

42658,8

170635,1

657,32–983,48

820,4

532,7

283769,3

983,48–1309,64

1146,56

858,86

737640,5

1309,64–1635,8

1472,72

1185,02

1404272,4

1635,8–1962

1798,9

1511,2

2283725,4

Итого

3081544,5

 ²= 3081544,5 /30 =102718,1 млн. руб.

Среднее квадратическое отклонение – это корень квадратный из дисперсии. Находится по формуле:

σ=  ( (X_i – X)²*f_i/ f_i₎

σ=  30827161,2 =5552,2 млн. руб.

σ=  102718,1 = 320,5 млн. руб.

Относительные показатели вариации

В общем виде они показывают отношение абсолютных показателей вариации к средней величине. К ним относятся:

Коэффициент осцилляции. Находится по формуле:

V_R= R / x * 100%

V_R₁= 24861 / 5535,3 * 100% = 449,1%

V_R₂=1957 / 287,7 *100% = 680,2%

Относительное линейное отклонение. Находится по формуле:

V_d= d / x * 100%

V_d₁ = 0,02 / 5535,3 * 100% = 0,0004%

V_d₁ = -0,03 / 287,7* 100% =-0,01%

Коэффициент вариации (характеризует однородность совокупности). Находится по формуле:

V_σ = σ / x * 100%

V_σ₁= 5552,2 / 5535,3 * 100% = 100% > 33% (совокупность неоднородная)

V_σ₁= 320,5/ 287,7* 100% = 111%> 33% (совокупность неоднородная)

г) Определение количественных характеристик распределения. К ним относятся:

– Показатель асимметрии. Находится по формуле:

As = ₃/  ³

₃=  (X_i – X)³* f_i/  f_i

где: ₃– центральный момент 3 – го порядка;

 ³- среднее квадратичное отклонение в кубе.

Таблица 10 – Расчет асимметрии по чистым активам, млн. руб.

Группы банков по чистым активам

Число банков, f

Середина интервала, X _i

X _i – Х

(X _i – Х)³

(X _i – Х)³ *f

425–4568,5

2496,75

-3038,55

-28054282211,7

-561085644234

4568,5–8712

6640,25

1104,95

134909479,5

674547397,5

8712–12855,5

10783,75

5248,45

144574997210,6

289149994421,2

12855,5–16999

14927,25

9391,95

828451932908,8

16999–21142,5

19070,75

13535,45

2479808228501,3

4959616457002,6

21142,5–25286

23214,25

17678,95

5525472255915,4

Итого

10213827610502,7

₃=10213827610502,7/ 30 = 340460920350,1

As = 340460920350,1/171157252096,6 = 1,9 > 0, асимметрия правосторонняя

Таблица 11 – Расчет асимметрии по прибыли, млн. руб.

Группы банков по прибыли

Число банков, f

Середина интервала, X _i

X _i – Х

(X _i – Х)³

(X _i – Х)³ *f

5–331,16

168,08

-119,62

-1711635,9

-41079261,6

331,16–657,32

494,24

206,54

8810742,7

35242970,8

657,32–983,48

820,4

532,7

151163900,8

983,48–1309,64

1146,56

858,86

633529919,5

1309,64–1635,8

1472,72

1185,02

1664090879,9

1635,8–1962

1798,9

1511,2

3451165884,9

Итого

3596493494,9

₃= 3596493494,9 / 30 = 119883116,5

As = 119883116,5/32921840,1= 3,6>0, асимметрия является правосторонней.

Чтобы определить является ли асимметрия существенной или несущественной рассчитывают отношение показателя асимметрии к среднеквадратическому отклонению:

As / _As

где: _As- среднеквадратическая ошибка асимметрии.

Она зависит от объема совокупности и рассчитывается по формуле:

_As=  6*(n – 1)/(n+1)*(n+3)

_As=  6 * (30 – 1)/(30+1)*(30+3) = 0,4

As / _As (по чистым активам) = 1,9 / 0,4 = 4,75>3

As / _As(по прибыли) = 3,6/ 0,4 = 9>3

Таким образом, As / _Asво всех случаях > 3  асимметрия существенна. Так как асимметрия существенна, эксцесс не рассчитывается.

д) Нахождение эмпирической функции и построение ее графика.

Для удобства вычислений вероятностей случайные величины нормируются, а затем по специальным таблицам находим плотность распределения нормированной случайной величины:

t = (x_i – x) / 

f ^| = ( f * k / )*  (t)

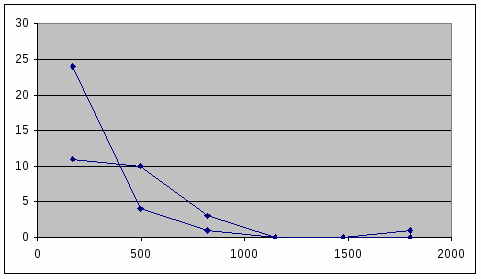
Таблица 14 – Расчет теоретических частот по чистым активам

Середина интервала, X _i

Число банков, f

X _i – Х

 (t)

f ^|

2496,75

-3038,55

-0,54

0,3448

8,0

6640,25

1104,95

0,19

0,3918

9,0

10783,75

5248,45

0,94

0,2565

6,0

14927,25

9391,95

1,69

0,0957

2,0

19070,75

13535,45

2,44

0,0203

23214,25

17678,95

3,18

0,0025

Итого

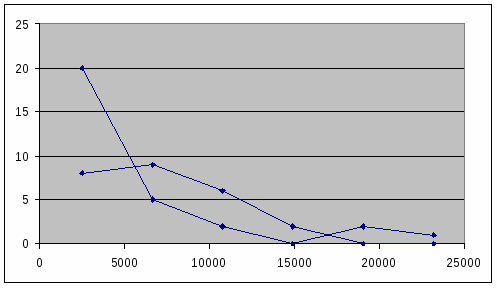
Таблица 15 – Расчет теоретических частот по прибыли

Середина интервала, X _i

Число банков, f

X _i – Х

 (t)

f ^|

168,08

-119,62

-0,37

0,3726

11,0

494,24

206,54

0,64

0,3251

10,0

820,4

532,7

1,66

0,1006

3,0

1146,56

858,86

2,68

0,0110

1472,72

1185,02

3,69

0,0004

1798,9

1511,2

4,71

Итого

Рисунок 3 – Эмпирическая и теоретическая функции распределения по чистым активам

Рисунок 4 – Эмпирическая и теоретическая функции распределения по прибыли

ж) Проверим гипотезу о том, что изучаемые признаки подчиняются нормальному закону распределения с помощью математического критерия Романовского:

 =(²_расч- (h-l1))/2 – (h-l1)

²_расч= (f – f ^|)²/ f

где: f – эмпирические частоты;

f ^| – теоретические частоты.

h – число групп;

l – число независимых параметров, которые необходимо знать, чтобы построить кривую теоретического распределения.

Таблица 16 – Проверка гипотезы по размеру чистых активов

Группы банков по чистым активам

Число банков, f

f ^|

(f- f ^|)

(f- f ^|)²

(f- f ^|)²/f

425–4568,5

8,0

12,0

1440

7,2

4568,5–8712

9,0

-4,0

16,0

3,2

8712–12855,5

6,0

-4,0

16,0

8,0

12855,5–16999

2,0

-2,0

4,0

0,0

16999–21142,5

2,0

4,0

2,0

21142,5–25286

1,0

Итого

22,4

²_расч= 22,4

 = (22,4 – (6–2–1))/(2*(6–2–1))= 7,9>3, следовательно, что гипотеза о соответствии распределения банков по размеру чистых активов закону нормального распределения отвергается

Таблица 17 – Проверка гипотезы по размеру прибыли

Группы банков по прибыли

Число банков, f

f ^|

(f- f ^|)

(f- f ^|)²

(f- f ^|)²/f

5–331,16

11,0

13,0

169,0

7,0

331,16–657,32

10,0

-6,0

36,0

9,0

657,32–983,48

3,0

-2,0

4,0

983,48–1309,64

1309,64–1635,8

1635,8–1962

1,0

Итого

²_расч= 21

 = (21 – (6–2–1))/(2*(6–2–1))= 7,3  3, следовательно, что гипотеза о соответствии распределения банков по размеру прибыли закону нормального распределения отвергается.

з) Определение границ, в которых с вероятностью 0,95 будет находиться среднее значение выбранных показателей в генеральной совокупности. Средняя ошибка выборки определяется по формуле:

 = ²/ n * (1 – (n/N))

где: n – число единиц в выборочной совокупности;

N – число единиц в генеральной совокупности.

=  30827161,2 /30*(1 – (30/200))= 1099,5 млн. руб.
= 102718,1 /30*(1 – (30/200))=63,5 млн. руб.

Предельная ошибка выборки определяется по формуле:

 =  * t

где t – коэффициент доверия, определяемый в зависимости от вероятности по таблицам. p = 0,95  t = 1,96

 = 1099,5*1,96 = 2155,02 млн. руб.

 = 63,5*1,96 = 124,4 млн. руб.

Границы среднего значения показателя определяются по формуле:

Х= Х  

где: Х – среднее арифметическое значение признака.

Х = 5535,3+ 2155,02 =7690,3 млн. руб.

Х = 5535,3 – 2155,02 =3380,5 млн. руб.

Х = 287,7 +124,4= 412,1 млн. руб.

Х = 287,7 – 124,4= 163,3 млн. руб.

Границы, в которых с вероятностью 0,95 будет находиться среднее значение показателя чистых активов в генеральной совокупности, лежит в пределах 3380,5 млн. руб.  Х  7690,3 млн. руб.

Границы, в которых с вероятностью 0,95 будет находиться среднее значение показателя прибыль в генеральной совокупности, лежит в пределах 163,3 млн. руб. Х  412,1 млн. руб.

По выше приведенным расчетам можно сделать следующие выводы:

– из 30 отобранных банков, наиболее часто встречаются банки с размером чистых активов 2604,04 млн. руб., с размером прибыли 178,8 млн. руб.;

– из отобранных банков 15 имеют размер чистых активов больше 3426,4 млн. руб. и 15 менее. И прибыль 15 банков больше 207 млн. руб., а у 15 менее;

– по данным абсолютных показателей вариации выборки по прибыли значительно ниже, чем по чистым активам;

– по данным относительных показателей совокупность неоднородная. Ассиметрия по чистым активам и по прибыли является правосторонней.

– границы, в которых с вероятностью 0,95 будет находиться среднее значение показателя чистых активов в генеральной совокупности, лежит в пределах

3380,5 млн. руб.  Х  7690,3 млн. руб., прибыль в пределах 163,3 млн. руб. Х  412,1 млн. руб.;

– гипотеза о том, что изучаемые признаки подчиняются нормальному закону распределения отвергается;

– зависимость между чистыми активами и прибылью по тесноте связи сильная, по направлению прямая;

– параметр коэффициента а не значим и не может распространяться на всю совокупность, а параметр b значим и его можно разместить на всю совокупность;

– коэффициент корреляции статистически значим.

Список используемой литературы

Конспект лекций
Статистика: учеб./ И.И. Елисеева А.В.

Листать вверх Листать вниз

Получить код

Скачать материал (0.05 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории экономика:

Денежные переводы

Интеллектуальная рабочая сила

Альфа-групп в Украине

Ценообразование в отрасли машиностроение

Особенности инфляционных процессов в современной российской экономике

Формирование цены труда в российской экономике

Інвестиційна модель Дж. М. Кейнса