Обработка статистической информации

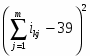
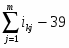
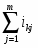
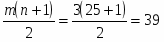
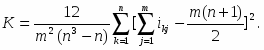
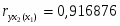
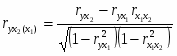
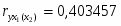
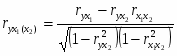
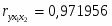
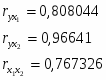
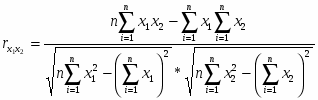
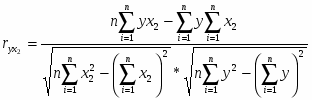
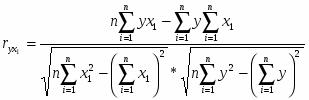
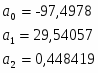
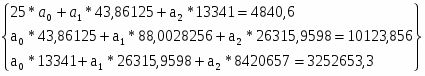
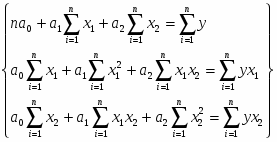
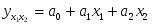
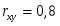
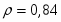
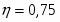
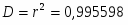
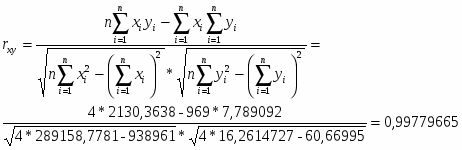
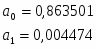
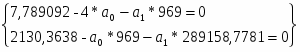
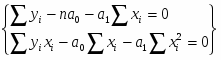
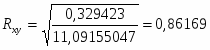
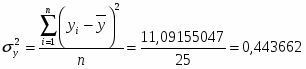
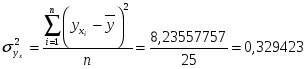
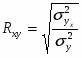
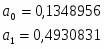
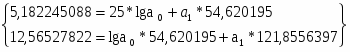
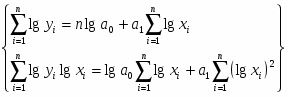
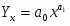
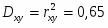
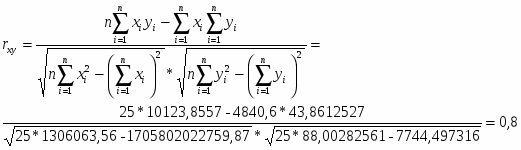
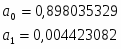
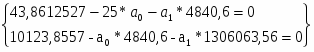
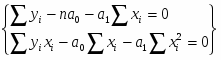
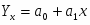
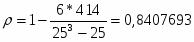
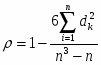
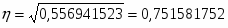
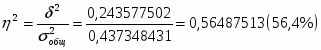
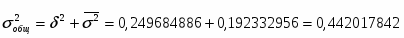
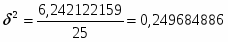
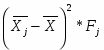
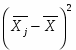
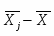
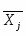
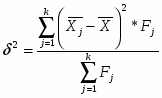
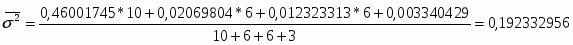
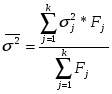
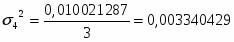
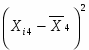
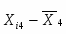
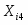
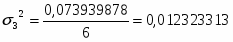
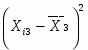
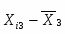
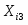
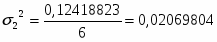
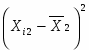
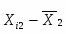
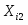
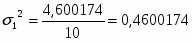
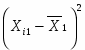
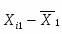
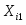
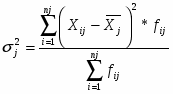
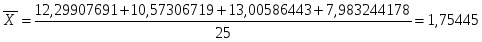
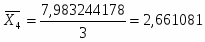
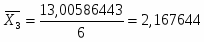
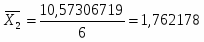
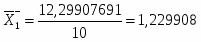
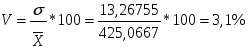
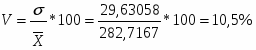
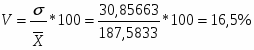
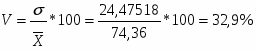
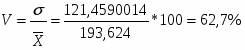
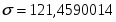
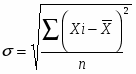
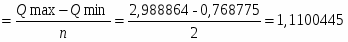
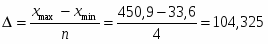
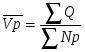
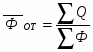
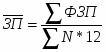
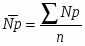
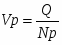
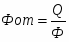
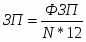МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА ЭКОНОМИКИ И ФИНАНСОВ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ

по дисциплине: СТАТИСТИКА

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.

816к Д.С. Гончарова

Санкт-Петербург 2010

Содержание

Введение

1. Относительные показатели

1.1 Среднемесячная заработная плата работника предприятия.

1.2 Доля заработной платы работников предприятия в объеме продукции

1.3 Фондоотдача основных фондов

2. Средние показатели

3. Группировка статистических данных

3.1 Простая аналитическая группировка

3.2 Комбинационная группировка

4. Проверка статистической совокупности на однородность

5. Определение взаимосвязи между двумя показателями (с использованием дисперсий)

6. Определение тесноты взаимосвязи между показателями с помощью коэффициента ранговой корреляции

7. Определение тесноты парной связи и формы связи с использованием корреляционно- регрессивного анализа между признаками

7.1 Определение тесноты парной связи и формы для всей статистической совокупности

7.1.1Линейная форма зависимости

7.1.2 Степенная форма зависимости

7.2 Определение тесноты парной связи и формы связи для групп, полученных в результате простой группировки

8. Сравнение и анализ расчетов

9. Исследование тесноты линейной множественной связи

9.1 Парные коэффициенты корреляции

9.2 Множественный коэффициент корреляции

9.3 Частные коэффициенты корреляции

9.4 Коэффициент конкордации

Заключение

Список литературы

Введение

Цель работы: изучение и освоение различных методов обработки статистической информации.

Для достижения поставленной цели необходимо выполнить следующие задачи:

определить относительные показатели по предприятиям;
рассчитать средние показатели по всей совокупности предприятий;
выполнить группировку статистической информации;
осуществить проверку статистической совокупности на однородность с использованием коэффициента вариации;
определить взаимосвязь (с использованием дисперсий) между показателями;
с использованием коэффициента ранговой корреляции определить тесноту взаимосвязи между показателями;
определить тесноту парной связи и форму связи с использованием корреляционно-регрессионного анализа между признаками;
исследовать линейную и нелинейную зависимость;
исследовать тесноту линейной множественной связи
определить:

Коэффициент конкордации.
Множественный коэффициент корреляции.
Парные коэффициенты корреляции.
Частные коэффициенты корреляции.

1. Относительные показатели

1.1 Среднемесячная заработная плата работника предприятия

Среднемесячная заработная плата рабочего по всей совокупности предприятий рассчитывается по формуле:

ФЗП- Фонд заработной платы (без учета выплат в различные фонды),

N- Среднесписочная численность работающих, чел.

Таблица 1.1

№

Фонд заработной платы (без учета выплат в различные фонды),

млн р

Среднесписочная числен-ность работающих, чел.

Среднемесячная заработная плата работника предприятия, тыс. р/мес.

33,6

205

13,65854

63,2

267

19,72534

241,0

668

30,06487

275,3

714

32,13119

159,7

544

24,46385

209,0

622

28,00107

251,8

683

30,7223

286,3

728

32,77244

149,3

526

23,65336

93,4

267

29,15106

406,9

868

39,0649

80,6

228

29,45906

278,2

718

32,28877

70,9

270

21,88272

92,0

413

18,56336

260,8

695

31,27098

71,6

364

16,39194

191,0

595

26,7507

450,9

914

41,1105

120,5

320

31,38021

79,7

256

25,94401

175,5

570

25,65789

38,1

229

13,86463

417,4

879

39,57148

343,9

798

35,9127

1.2 Фондоотдача основных фондов

Фондоотдача основных фондов по всей совокупности предприятий рассчитывается по формуле:

Q- Объем товарной продукции,

Ф- Среднегодовая стоимость основных фонов.

Таблица 1.2

№

Объем товарной продукции,

млн. р.

Среднегодовая стоимость основных фондов, млн. р.

Фондоотдача основных фондов

163,8

180,1

0,909495

236,5

294,5

0,803056

843,3

420,8

2,00404

1005,9

469,7

2,14158

696,3

426,9

1,631061

1031,3

552,4

1,866944

1361,2

664,6

2,048149

1712,9

784,2

2,184264

538,9

341,8

1,576653

350,4

438

0,8

2149,9

825,4

2,604677

352,8

179,8

1,96218

1187,1

551,5

2,152493

262,4

323,4

0,811379

438,8

354,2

1,238848

1150,5

551,9

2,084617

249,4

228,3

1,092422

655,3

367,4

1,783615

2549,5

930,3

2,740514

536,8

179,6

2,988864

311,2

404,8

0,768775

809,7

473,3

1,710754

166,7

180,4

0,924058

2185,1

828,3

2,638054

2066,2

862,8

2,394761

1.3 Месячная производительность труда одного рабочего

Месячная производительность труда одного рабочего по всей совокупности предприятий рассчитывается по формуле:

Q- Объем товарной продукции,

Np- Среднесписочная численность рабочих.

Таблица 1.3

№

Объем товарной продукции,

млн. р.

Среднесписочная численность рабочих, чел.

Месячная производительность труда одного рабочего, тыс. р/чел.

163,8

205

0,0000665854

236,5

267

0,0000738140

843,3

668

0,0001052021

1005,9

714

0,0001174020

696,3

544

0,0001066636

1031,3

622

0,0001381699

1361,2

683

0,0001660810

1712,9

728

0,0001960737

538,9

526

0,0000853771

350,4

267

0,0001093633

2149,9

868

0,0002064036

352,8

228

0,0001289474

1187,1

718

0,0001377786

262,4

270

0,0000809877

438,8

413

0,0000885391

1150,5

695

0,0001379496

249,4

364

0,0000570971

655,3

595

0,0000917787

2549,5

914

0,0002324489

536,8

320

0,0001397917

311,2

256

0,0001013021

809,7

570

0,0001183772

166,7

229

0,0000606623

2185,1

879

0,0002071578

2066,2

798

0,0002157686

2. Средние показатели

Средние показатели по всей совокупности предприятий рассчитываются по следующим формулам:

Таблица 2.1

№

Среднеспи-сочная численность рабочих, чел.

Среднемесячная заработная плата работника, тыс. р/мес.

Фондоотдача основных фондов

Среднемесячная производительность труда одного рабочего, тыс. р/чел.

205

13,65854

0,909495

0,0000665854

267

19,72534

0,803056

0,0000738140

668

30,06487

2,00404

0,0001052021

714

32,13119

2,14158

0,0001174020

544

24,46385

1,631061

0,0001066636

622

28,00107

1,866944

0,0001381699

683

30,7223

2,048149

0,0001660810

728

32,77244

2,184264

0,0001960737

526

23,65336

1,576653

0,0000853771

267

29,15106

0,8

0,0001093633

868

39,0649

2,604677

0,0002064036

228

29,45906

1,96218

0,0001289474

718

32,28877

2,152493

0,0001377786

270

21,88272

0,811379

0,0000809877

413

18,56336

1,238848

0,0000885391

695

31,27098

2,084617

0,0001379496

364

16,39194

1,092422

0,0000570971

595

26,7507

1,783615

0,0000917787

914

41,1105

2,740514

0,0002324489

320

31,38021

2,988864

0,0001397917

256

25,94401

0,768775

0,0001013021

570

25,65789

1,710754

0,0001183772

229

13,86463

0,924058

0,0000606623

879

39,57148

2,638054

0,0002071578

798

35,9127

2,394761

0,0002157686

Среднее

533,64

30,236364

1,947784

0,143742

3. Группировка статистических данных

3.1 Простая аналитическая группировка

Величина равных интервалов определяется по формуле:

где и  максимальное и минимальное значение признака;

n  заданное количество интервалов группировки

Анализ данных таблицы 3.1 показывает, что самое большое количество предприятий находится в первой группе, а наименьшее в четвертой. Фондоотдача основных фондов, среднесписочная численность рабочих и среднемесячная заработная плата работника предприятия находятся в прямой зависимости от фонда заработной платы.

3.2 Комбинационная группировка

Согласно исходным данным группировочные признаки: фонд заработной платы и фондоотдача основных фондов, а результативными являются среднесписочная численность рабочих, производительность труда одного рабочего.

∆₁=104,325

∆₂

Таблица 3.2

Номер

групппы

Группы фирм

Номера фирм

Среднесписочная численность рабочих, чел.

Производительность труда одного рабочего, р/чел.

По Фонду заработной платы, тыс.р.

По фондоотдаче основных фондов

Суммарная

Средняя

Суммарная

Средняя

33,6-137,925

0,768775-1,8788195

1,2,10,

14,15,

17,21,23

2271

283,875

0,0006383509

0,0000797939

1,8788195-2,988864

12,20

548

274

0,0002687390

0,0001343695

Итого:

2819

281,9

0,0009070899

0,00009070899

137,925-242,25

0,768775-1,8788195

5,6,9,18,

2857

571,4

0,0005403664

0,000108073

1,8788195-2,988864

668

0,0001052021

Итого:

3525

587,5

0,0006455685

0,000107595

III

242,25- 346,575

0,768775-1,8788195

1,8788195-2,988864

4,7,8,13,16,25

4336

722,66666

0,0009710535

0,000161842

Итого:

4336

722,66666

0,0009710535

0,000161842

346,575-450,9

0,768775-1,8788195

1,8788195-2,988864

11,19,24

2661

887

0,0006460103

0,000215337

Итого:

2661

887

0,0006460103

0,000215337

Наибольшее количество предприятий состоит в первой группе, наибольшая производительность труда одного рабочего у предприятий входящих в 4 группу, а так же в этой группе наибольшие показатели среднесписочной численности рабочих. Среднесписочная численность рабочих и производительность труда одного рабочего находятся в прямой зависимости с фондом заработной платы и фондоотдачей основных фондов.

4. Проверка статистической совокупности на однородность

В своей работе проверку статистической совокупности на однородность я произвожу с использованием коэффициента вариации по признаку Фонд заработной платы.

Таблица 4.1

ФЗП(Xi)

Xi-X

(Xi-X)^2

33,6

-160,024

25607,68

63,2

-130,424

17010,42

241

47,376

2244,485

275,3

81,676

6670,969

159,7

-33,924

1150,838

209

15,376

236,4214

251,8

58,176

3384,447

286,3

92,676

8588,841

149,3

-44,324

1964,617

93,4

-100,224

10044,85

406,9

213,276

45486,65

80,6

-113,024

12774,42

278,2

84,576

7153,1

70,9

-122,724

15061,18

-101,624

10327,44

260,8

67,176

4512,615

71,6

-122,024

14889,86

191

-2,624

6,885376

450,9

257,276

66190,94

120,5

-73,124

5347,119

79,7

-113,924

12978,68

175,5

-18,124

328,4794

38,1

-155,524

24187,71

417,4

223,776

50075,7

343,9

150,276

22582,88

4840,6

368807,2

Среднее линейное отклонение – это среднее значение отклонений вариантов признака от их средней величины:

X=193,624

xi – варианты признака

х – средняя величина признака

n – численность единиц совокупности

На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.

Далее я рассчитываю коэффициенты вариации для простой группировки.

Для первой группы:

Таблица 4.2

Xi-X10

(Xi-X)^2

33,6

-40,76

1661,378

63,2

-11,16

124,5456

93,4

19,04

362,5216

80,6

6,24

38,9376

70,9

-3,46

11,9716

17,64

311,1696

71,6

-2,76

7,6176

120,5

46,14

2128,9

79,7

5,34

28,5156

38,1

-36,26

1314,788

743,6

5990,344

X=74,36

σ=24,47518

Нужно произвести перегруппировку.

Для второй группы:

Таблица 4.3

Xi-X6

(Xi-X)^2

241

53,4167

2853,34

159,7

-27,8833

777,4803

209

21,4167

458,6736

149,3

-38,2833

1465,614

191

3,41667

11,67361

175,5

-12,0833

146,0069

1125,5

5712,788

X=187,5833

σ=30,85663

На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

Для третьей группы:

Таблица 4.4

Xi-X6

(Xi-X)^2

275,3

-7,41667

55,00694

251,8

-30,9167

955,8403

286,3

3,583333

12,84028

278,2

-4,51667

20,40028

260,8

-21,9167

480,3403

343,9

61,18333

3743,4

1696,3

5267,828

X=282,7167

σ=29,63058

Для четвертой группы:

Таблица 4.5

Xi-X

(Xi-X)^2

406,9

-18,1667

330,0278

450,9

25,83333

667,3611

417,4

-7,66667

58,77778

1275,2

1056,167

X=425,0667

σ=13,26755

5. Определение взаимосвязи между двумя показателями (с использованием дисперсий)

Все явления общественной жизни взаимосвязаны и взаимообусловлены. Задача состоит в том, чтобы выявить и измерить связи и зависимости между изучаемыми явлениями.

Эмпирическое корреляционное отношение – это показатель тесноты связи между взаимосвязанными явлениями.

Таблица 5.1

№

Фонд заработной платы, млн. р.

Фондоотдача основных фондов

33,6-137,925

0,909494725

0,803056027

0,8

1,9621802

0,811379097

1,238848108

1,092422251

2,988864143

0,768774704

0,92405765

137,925-242,25

2,004039924

1,631061138

1,866944243

1,576653013

1,783614589

1,710754278

242,25- 346,575

2,141579732

2,048149263

2,184264218

2,1524932

2,084616778

2,394761242

346,575-450,9

2,60467652

2,740513813

2,638053845

Я определяю взаимосвязь между фондом заработной платы и фондоотдачей основных фондов.

Далее я рассчитываю среднее значение фондоотдачи основных фондов:

Рассчитываю для каждой группы групповую дисперсию.

Групповая дисперсия рассчитывается по формуле:

Дисперсия для 1 группы:

Таблица 5.2

0,909494725

-0,320412965

0,102664468

0,803056027

-0,426851663

0,182202343

0,8

-0,429907691

0,184820622

1,9621802

0,73227251

0,536223028

0,811379097

-0,418528593

0,175166184

1,238848108

0,008940418

0,0000799

1,092422251

-0,137485439

0,018902246

2,988864143

1,758956452

3,0939278

0,768774704

-0,461132987

0,212643632

0,92405765

-0,305850041

0,093544247

Итого:

4,600174502

Дисперсия для 2 группы:

Таблица 5.3

2,004039924

0,24186206

0,05849726

1,631061138

-0,131116726

0,0171916

1,866944243

0,104766379

0,01097599

1,576653013

-0,185524851

0,03441947

1,783614589

0,021436725

0,00045953

1,710754278

-0,051423586

0,00264439

Итого:

0,12418823

Дисперсия для 3 группы:

Таблица 5.4

2,141579732

0,005654493

3,19733E-05

2,048149263

-0,087775976

0,007704622

2,184264218

0,048338979

0,002336657

2,1524932

-0,173745039

0,030187338

2,084616778

-0,051308461

0,002632558

2,394761242

0,258836003

0,066996077

Итого:

0,073939878

Дисперсия для 4 группы:

Таблица 5.5

2,60467652

-0,056404872

0,00318151

2,740513813

0,07943242

0,006309509

2,638053845

-0,023027548

0,000530268

Итого:

0,010021287

Далее я рассчитываю среднюю внутригрупповую дисперсию :

Внутригрупповая дисперсия находится по формуле:

Далее я рассчитываю межгрупповую дисперсию:

Межгрупповая дисперсия рассчитывается по формуле:

Таблица 5.6

№

Кол-во

1,229907691

-0,5245424

0,275144748

2,751447479

1,762177864

0,00772776

0,000059718

0,000358309

2,167644072

0,41319396

0,170729252

1,024375512

2,661081393

0,90663128

0,821980286

2,465940859

Итого:

6,242122159

Далее рассчитываю общую дисперсию:

Рассчитываю коэффициент детерминации:

Рассчитываю эмпирическое корреляционное отношение:

Изменение фонда заработной платы влияет на изменение фондоотдачи основных фондов на 56,4%, между фондом заработной платы и фондоотдачей основных фондов предприятия существует тесная положительная связь.

6. Определение тесноты взаимосвязи между показателями с помощью коэффициента ранговой корреляции

Коэффициент ранговой корреляции находится по формуле:

Таблица 6.1

№

Фонд заработной платы, млн.р.

Фондоотдача основных фондов

Ранг ФЗП

Ранг Ф

d_k

d²_k

33,6

0,909494725

-4

63,2

0,803056027

241

2,004039924

275,3

2,141579732

159,7

1,631061138

209

1,866944243

251,8

2,048149263

286,3

2,184264218

149,3

1,576653013

93,4

0,8

406,9

2,60467652

80,6

1,9621802

-7

278,2

2,1524932

70,9

0,811379097

1,238848108

260,8

2,084616778

71,6

1,092422251

-2

191

1,783614589

450,9

2,740513813

120,5

2,988864143

-15

225

79,7

0,768774704

175,5

1,710754278

38,1

0,92405765

-4

417,4

2,638053845

343,9

2,394761242

Итого:

4840,6

43,8612527

414

7. Определение тесноты парной связи и формы связи с использованием корреляционно- регрессивного анализа между признаками

Тесноту парной связи и форму связи с использованием корреляционно-регрессивного анализа я определяю между фондом заработной платы и фондоотдачей основных фондов.

7.1 Определение тесноты парной связи и формы для всей статистической совокупности

7.1.1Линейная форма зависимости

Таблица 7.1

№

x²

y²

Y_x

33,6

0,909494725

30,55902277

1128,96

0,827180655

1,046650876

63,2

0,803056027

50,75314092

3994,24

0,644898983

1,177574095

241

2,004039924

482,9736217

58081

4,016176017

1,963998029

275,3

2,141579732

589,5769001

75790,09

4,586363747

2,115709732

159,7

1,631061138

260,4804638

25504,09

2,660360437

1,604401483

209

1,866944243

390,1913469

43681

3,485480808

1,822459413

251,8

2,048149263

515,7239844

63403,24

4,194915402

2,011767312

286,3

2,184264218

625,3548457

81967,69

4,771010175

2,164363632

149,3

1,576653013

235,3942949

22290,49

2,485834725

1,558401433

93,4

0,8

74,72

8723,56

0,64

1,311151164

406,9

2,60467652

1059,842876

165567,61

6,784339776

2,69778729

80,6

1,9621802

158,1517241

6496,36

3,850151138

1,254535717

278,2

2,1524932

598,8236083

77395,24

4,633226978

2,128536669

70,9

0,811379097

57,52677798

5026,81

0,658336039

1,211631825

1,238848108

113,974026

8464

1,534744636

1,304958849

260,8

2,084616778

543,6680558

68016,64

4,345627113

2,051575047

71,6

1,092422251

78,2174332

5126,56

1,193386375

1,214727982

191

1,783614589

340,6703865

36481

3,181281002

1,742843942

450,9

2,740513813

1235,697678

203310,81

7,510415958

2,892402886

120,5

2,988864143

360,1581292

14520,25

8,933308863

1,431016679

79,7

0,768774704

61,27134387

6352,09

0,591014545

1,250554944

175,5

1,710754278

300,2373759

30800,25

2,926680201

1,674286175

38,1

0,92405765

35,20659645

1451,61

0,85388254

1,066554744

417,4

2,638053845

1101,123675

174222,76

6,95932809

2,744229648

343,9

2,394761242

823,5583913

118267,21

5,734881408

2,41913314

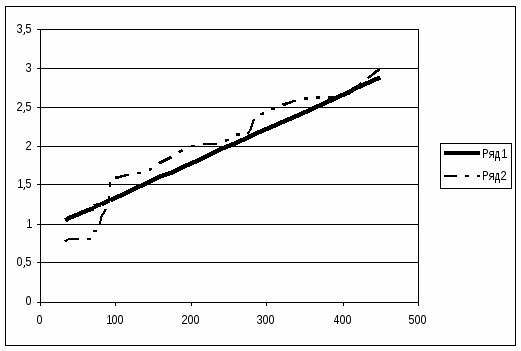
Итого:

4840,6

43,8612527

10123,8557

1306063,56

88,00282561

43,8612527

Рисунок 7.1

7.1.2 Степенная форма зависимости

Таблица 7.2

№

lgx

lgy

lgxlgy

(lgx)²

Y_x

33,6

0,909494725

1,5263393

-0,041199815

-0,062884896

2,32971159

0,7631503

63,2

0,803056027

1,8007171

-0,095254154

-0,171525782

3,242581996

1,0420802

241

2,004039924

2,382017

0,301906369

0,719146117

5,674005191

2,0161849

275,3

2,141579732

2,4398062

0,330734248

0,806927473

5,952654349

2,1529068

159,7

1,631061138

2,2033049

0,21247024

0,468136725

4,854552553

1,6459264

209

1,866944243

2,3201463

0,271131348

0,62906439

5,383078789

1,8794161

251,8

2,048149263

2,4010557

0,311361603

0,747596561

5,765068598

2,0602409

286,3

2,184264218

2,4568213

0,339305171

0,833612189

6,035971136

2,1949018

149,3

1,576653013

2,1740598

0,197736125

0,429890162

4,726536048

1,5921726

93,4

0,8

1,9703469

-0,096910013

-0,190946341

3,882266813

1,2634054

406,9

2,60467652

2,6094877

0,415753795

1,08490441

6,809426003

2,6103113

80,6

1,9621802

1,906335

0,292738889

0,558058402

3,634113292

1,1748423

278,2

2,1524932

2,4443571

0,332941788

0,813828632

5,974881758

2,1640595

70,9

0,811379097

1,8506462

-0,090776185

-0,167994605

3,424891488

1,10286

1,238848108

1,9637878

0,093018062

0,182667738

3,856462631

1,2540319

260,8

2,084616778

2,4163076

0,319026229

0,770865497

5,838542355

2,0962277

71,6

1,092422251

1,854913

0,038390538

0,071211108

3,44070232

1,1082156

191

1,783614589

2,2810334

0,251301016

0,573226003

5,203113222

1,7977819

450,9

2,740513813

2,6540802

0,437831995

1,162041245

7,044141895

2,745871

120,5

2,988864143

2,080987

0,475506175

0,989522191

4,330507089

1,4325096

79,7

0,768774704

1,9014583

-0,114200916

-0,217148281

3,615543748

1,1683554

175,5

1,710754278

2,2442771

0,233187635

0,523337674

5,036779795

1,7243012

38,1

0,92405765

1,580925

-0,034300933

-0,054227202

2,499323779

0,8119427

417,4

2,638053845

2,6205524

0,421283656

1,103995914

6,867295116

2,6433103

343,9

2,394761242

2,5364322

0,379262221

0,9619729

6,433488183

2,4025357

Итого:

4840,6

43,8612527

54,620195

5,182245088

12,56527822

121,8556397

42,847542

Рисунок 7.2

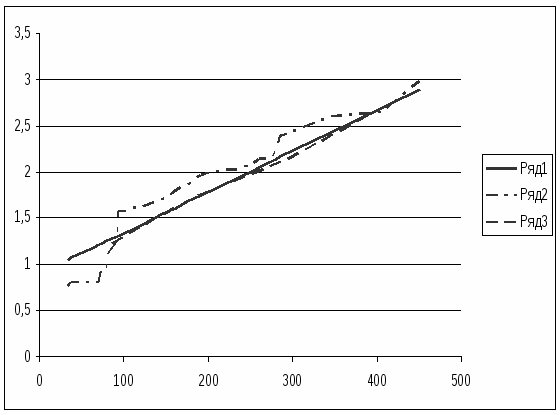
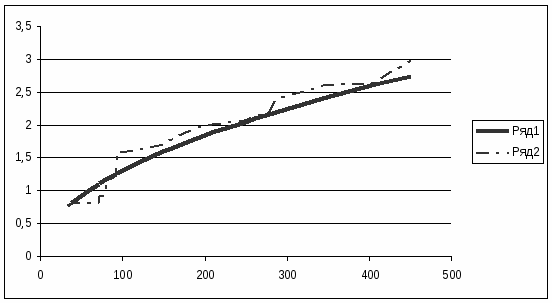
7.2 Определение тесноты парной связи и формы связи для групп, полученных в результате простой группировки

Таблица 7.3

№

X²

Y²

Y_x

85,7625

1,229908

105,479985

7355,206406

1,51267369

1,2471831

190,0875

1,762178

334,968011

36133,25766

3,1052713

1,7139097

294,4125

2,135925

628,843019

86678,72016

4,56217561

2,1806363

398,7375

2,661081

1061,07279

158991,5939

7,08135209

2,6473629

Итого:

969

7,789092

2130,3638

289158,7781

16,2614727

7,789092

Рисунок 7.3

При сравнении пунктов 7.1 и 7.2 видно, что в обоих пунктах коэффициент корреляции достаточно велик, что свидетельствует о сильной и прямой связи между фондом заработной платы и фондоотдачей основных фондов.

8. Сравнение и анализ расчетов

При расчетах в 5, 6 и 7 пунктах видно, что между объемом товарной продукции и среднемесячной заработной платой работника предприятия присутствует прямая положительная связь.

9. Исследование тесноты линейной множественной связи

Исследование тесноты множественной линейной связи между результативным признаком объемом товарной продукции и двумя факторными среднемесячной заработной платой работника предприятия и фондоотдачей основных фондов.

Вид уравнения множественной регрессии:

Таблица 9.1

X₁

X₂

X₁²

X₂²

X₁X₂

X₁Y

X₂Y

Y_x_1x2

33,6

0,909495

205

0,82718066

42025

186,446419

30,559023

6888

21,2951101

63,2

0,803056

267

0,64489898

71289

214,415959

50,753141

16874,4

45,9528289

241

2,00404

668

4,01617602

446224

1338,69867

482,97362

160988

261,246605

275,3

2,14158

714

4,58636375

509796

1529,08793

589,5769

196564,2

285,936884

159,7

1,631061

544

2,66036044

295936

887,297259

260,48046

86876,8

194,62464

209

1,866944

622

3,48548081

386884

1161,23932

390,19135

129998

236,569445

251,8

2,048149

683

4,1949154

466489

1398,88595

515,72398

171979,4

269,275905

286,3

2,184264

728

4,77101018

529984

1590,14435

625,35485

208426,4

293,475674

149,3

1,576653

526

2,48583472

276676

829,319485

235,39429

78531,8

184,945851

93,4

0,8

267

0,64

71289

213,6

74,72

24937,8

45,8625521

406,9

2,604677

868

6,78433978

753424

2260,85922

1059,8429

353189,2

368,673556

80,6

1,96218

228

3,85015114

51984

447,377086

158,15172

18376,8

62,7056787

278,2

2,152493

718

4,63322698

515524

1545,49012

598,82361

199747,6

288,05295

70,9

0,811379

270

0,65833604

72900

219,072356

57,526778

19143

47,5439542

1,238848

413

1,53474464

170569

511,644269

113,97403

37996

124,295552

260,8

2,084617

695

4,34562711

483025

1448,80866

543,66806

181256

275,734204

71,6

1,092422

364

1,19338638

132496

397,6417

78,217433

26062,4

97,997517

191

1,783615

595

3,181281

354025

1061,25068

340,67039

113645

222,000526

450,9

2,740514

914

7,51041596

835396

2504,82962

1235,6977

412122,6

393,313542

120,5

2,988864

320

8,93330886

102400

956,436526

360,15813

38560

134,289059

79,7

0,768775

256

0,59101454

65536

196,806324

61,271344

20403,2

40,0075298

175,5

1,710754

570

2,9266802

324900

975,129939

300,23738

100035

208,637715

38,1

0,924058

229

0,85388254

52441

211,609202

35,206596

8724,9

32,4873636

417,4

2,638054

879

6,95932809

772641

2318,84933

1101,1237

366894,6

374,59215

343,9

2,394761

798

5,73488141

636804

1911,01947

823,55839

274432,2

331,083208

Итого:

4840,6

43,86125

13341

88,0028256

8420657

26315,9598

10123,856

3252653,3

4840,6

9.1 Парные коэффициенты корреляции

Парный коэффициент корреляции находится по формуле:

9.2 Множественный коэффициент корреляции

Множественный коэффициент корреляции находится по формуле:

9.3Частные коэффициенты корреляции

Частный коэффициент корреляции находится по формуле:

9.4 Коэффициент конкордации

Коэффициент конкордации находится по формуле:

n_i– число неразличимых элементов (рангов) в i –й группе признака X_j ;

m_j– число групп из неразличимых рангов.

Таблица 9.2

№

Фонд заработной платы, млн. р.

Фондоотдача основных фондов

Среднесписочная численность рабочих, чел.

Ранги

ФЗП

Фот

33,6

0,909495

205

63,2

0,803056

267

241

2,00404

668

275,3

2,14158

714

159,7

1,631061

544

209

1,866944

622

251,8

2,048149

683

286,3

2,184264

728

149,3

1,576653

526

93,4

0,8

267

406,9

2,604677

868

80,6

1,96218

228

278,2

2,152493

718

70,9

0,811379

270

1,238848

413

260,8

2,084617

695

71,6

1,092422

364

191

1,783615

595

450,9

2,740514

914

120,5

2,988864

320

79,7

0,768775

256

175,5

1,710754

570

38,1

0,924058

229

417,4

2,638054

879

343,9

2,394761

798

Таблица 9.3

№

Ранги

ЗП

Фот

-32

1024

-28

784

289

-5

121

529

-8

-22

484

841

-16

256

400

-24

576

-13

169

196

-18

324

1225

-28

784

-2

-28

784

1024

676

Итого:

10676

Заключение

Настоящая работа ставила перед собой цель освоения практических навыков обработки статистической информации. В процессе работы было рассмотрено 25 предприятий. Вначале были рассчитаны относительные и средние показатели для каждого предприятия. На основе рассчитанных относительных, а так же абсолютных признаков была сделана простая аналитическая группировка по фонду заработной платы, в результате которой был сделан вывод о наличии прямой связи между ним и результативными показателями: фондоотдачей основных фондов, среднесписочной численностью рабочих, среднемесячной заработной платой работника предприятия, производительностью труда одного рабочего.

Затем совокупность предприятий была проверена на однородность по признаку фонд заработной платы, в результате чего было выяснено, что вся совокупность предприятий неоднородна по этому показателю, но одна группа, полученная в результате простой группировки оказалась неоднородна по данному признаку, так как коэффициент вариации в этом случае оказался выше 25%

Затем вся совокупность предприятий была проанализирована по двум признакам: фонд заработной платы и фондоотдачей основных фондов для выявления наличия и тесноты связи.

С использованием дисперсий было вычислено эмпирическое корреляционное отношение 75%. Коэффициент ранговой корреляции равен 84%. Затем были рассчитаны показатели тесноты связи: парный коэффициент корреляции оказался равен 0,8.

Далее был проведен анализ по всей совокупности предприятий на наличие и тесноту множественной связи между результативным признаком фондом заработной платы и двумя факторными признаками: фондоотдачей основных фондов и среднесписочной численностью рабочих.

С использованием рангов был рассчитан коэффициент конкордации – 0,91. Кроме этого был вычислен множественный коэффициент корреляции – 0,97. Поэтому можно утверждать, что между результативным и факторными признаками существует сильная связь. Так же были рассчитаны парные коэффициенты корреляции и частные коэффициенты корреляции, на основе которых можно утверждать, что фонд заработной платы зависит от фондоотдачи основных фондов и среднесписочной численности рабочих.

Список литературы

Богородская Н.А. Статистика. Методы анализа статистической информации: Методические указания к практическим занятиям / СПбГУАП, СПб., 2008. 158 с.
Теория статистики: Учебник / Под ред. Г.Л.Громыко.  2-е изд., перераб. и доп.  М.: ИНФРА-М, 2005.  476 с.

Листать вверх Листать вниз

Получить код

Скачать материал (0.13 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории экономика:

Рыночная экономика

Место бизнес-плана в планировании деятельности существующего предприятия

Анализ финансово-хозяйственной деятельности предприятия

Політекономія як суспільно-економічна наука

Нары м ні, пайда болуы, ызметі 4

Банки

Препятствие на пути прямых инвестиций: антимонопольное законодательство или несовершенство налоговой системы