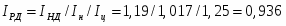
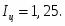
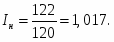
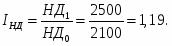
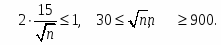
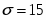
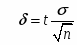
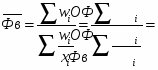
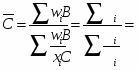
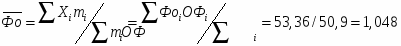
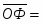
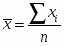
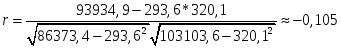
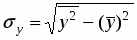
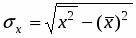
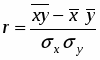
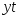
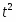
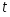
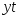
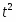
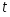
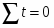
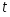
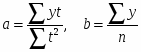
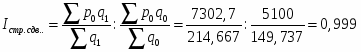
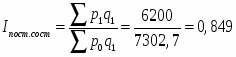
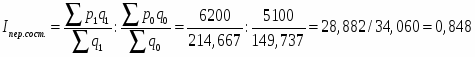
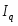
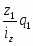
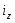
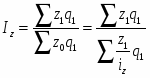
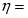
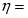
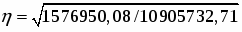
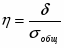
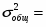
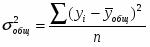
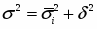
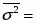
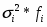
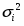
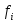
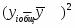
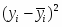
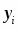
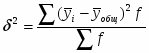
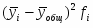
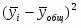
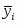
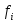
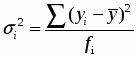
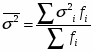
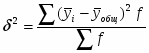
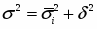
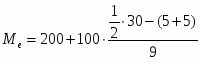
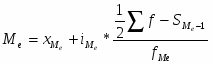
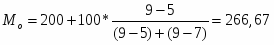
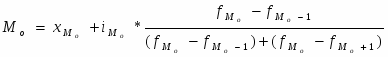Задание 1

1. По данным таблицы 1 произведите группировку 30 коммерческих банков по величине прибыли, образовав 6 групп с заданными интервалами:

а) До 100; б) 100-200; в) 200-300; г) 300-500; д) 500-700; е) 700 и более.

Таблица 1 Список крупнейших банков России по размеру капитала на 01.01.97 г, (млрд. руб.)

Ранг

Название банка

Город

Кредит- ные вложения

Объем вложений в ценные бумаги

Прибыль

1.

Национальный резервный банк

Москва

2439

4994

645

2.

ОНЭКСИМбанк

Москва

15581

1547

266

3.

Международная финансовая компания

Москва

7612

510

512

4.

Инкомбанк

Москва

9432

2975

744

5.

ТОКОбанк

Москва

4318

852

282

6.

Империал

Москва

5398

654

429

7.

Автобанк

Москва

3900

1684

913

8.

Международный московский банк

Москва

5077

1173

290

9.

СБС

Москва

3256

4556

175

10.

Международный промышленный банк

Москва

3419

597

18

11.

Башкредитбанк

Уфа

778

551

417

12.

Российский кредит

Москва

6019

1429

367

13.

Мосбизнесбанк

Москва

4899

1837

481

14.

МЕНАТЕП

Москва

9035

786

146

15.

Московский индустриальный банк

Москва

1742

469

365

16.

Промстройбанк России

Москва

2890

1115

239

17.

Промышленно-строительный банк

С.-Петербург

1600

991

306

18.

Уникомбанк

Москва

1605

439

57

19.

Газпромбанк

Москва

1764

673

265

20.

Возрождение

Москва

2236

532

158

21.

Мост-банк

Москва

4423

2020

129

22.

Московский деловой мир

Москва

981

543

340

23.

Межкомбанк

Москва

2004

1040

167

24.

Нефтехимбанк

Москва

1216

838

41

25.

Ситибанк Т/О

Москва

1490

1041

258

26.

Ланта-банк

Москва

545

44

35

27.

Альба-альянс

147

426

298

28.

ИнтерТЭКбанк

Москва

1039

167

57

29.

Мосстройэкономбанк

Москва

1091

27

221

30.

Росэстбанк

Тольятти

511

195

243

1.По каждой группе рассчитайте:

- средний размер прибыли;

- средний размер кредитных вложений;

- средний объем вложений в ценные бумаги.

Результаты оформите в аналитической таблице. Сделайте выводы.

2. По данным таблицы определите модальное и медианное значения прибыли.

3. По показателю размер кредитных вложений рассчитайте:

- общую дисперсию по правилу сложения дисперсии;

- общую дисперсию любым другим способом;

- эмпирическое корреляционное отношение.

Сделайте выводы.

Решение

1.Строим ранжированный ряд банков по прибыли.

Ранг

№

Название банка

Город

Кредит- ные вложе-ния

Объем вложений в ценные бумаги

При-быль

1.

10.

Международный промышленный банк

Москва

3419

597

18

2.

26.

Ланта-банк

Москва

545

44

35

3.

24.

Нефтехимбанк

Москва

1216

838

41

4.

18.

Уникомбанк

Москва

1605

439

57

5.

28.

ИнтерТЭКбанк

Москва

1039

167

57

6.

21.

Мост-банк

Москва

4423

2020

129

7.

14.

МЕНАТЕП

Москва

9035

786

146

8.

20.

Возрождение

Москва

2236

532

158

9.

23.

Межкомбанк

Москва

2004

1040

167

10.

9.

СБС

Москва

3256

4556

175

11.

29.

Мосстройэкономбанк

Москва

1091

27

221

12.

16.

Промстройбанк России

Москва

2890

1115

239

13.

30.

Росэстбанк

Тольятти

511

195

243

14.

25.

Ситибанк Т/О

Москва

1490

1041

258

15.

19.

Газпромбанк

Москва

1764

673

265

16.

2.

ОНЭКСИМбанк

Москва

15581

1547

266

17.

5.

ТОКОбанк

Москва

4318

852

282

18.

8.

Международный московский банк

Москва

5077

1173

290

19.

27.

Альба-альянс

147

426

298

20.

17.

Промышленно-строительный банк

С.-Петербург

1600

991

306

21.

22.

Московский деловой мир

Москва

981

543

340

22.

15.

Московский индустриальный банк

Москва

1742

469

365

23.

12.

Российский кредит

Москва

6019

1429

367

24.

11.

Башкредитбанк

Уфа

778

551

417

25.

6.

Империал

Москва

5398

654

429

26.

13.

Мосбизнесбанк

Москва

4899

1837

481

27.

3.

Международная финансовая компания

Москва

7612

510

512

28.

1.

Национальный резервный банк

Москва

2439

4994

645

29.

4.

Инкомбанк

Москва

9432

2975

744

30.

7.

Автобанк

Москва

3900

1684

913

Группировочная таблица:

№ интервала

интервал

Ранги точек интервала

Количество точек интервала

1-й интервал

До 100

1-5

5

2-й интервал

100-200

6-10

5

3-й интервал

200-300

11-19

9

4-й интервал

300-500

20-26

7

5-й интервал

500-700

27-28

2

6-й интервал

700 и более

29-30

2

По каждой группе определяем общий размер прибыли, общий размер кредитных вложений и общий объем вложений в ценные бумаги. Составляем вспомогательную таблицу:

Интервал

Кредитные вложения

Объем вложений в ценные бумаги

Прибыль

До 100

3419

597

18

545

44

35

1216

838

41

1605

439

57

1039

167

57

Итого в 1 –м интервале

7824

2085

208

100-200

4423

2020

129

9035

786

146

2236

532

158

2004

1040

167

3256

4556

175

Итого во 2 –м интервале

20954

8934

775

200-300

1091

27

221

2890

1115

239

511

195

243

1490

1041

258

1764

673

265

15581

1547

266

4318

852

282

5077

1173

290

147

426

298

Итого в 3 –м интервале

32869

7049

2362

300-500

1600

991

306

981

543

340

1742

469

365

6019

1429

367

778

551

417

5398

654

429

4899

1837

481

Итого в 4 –м интервале

21417

6474

2705

500-700

7612

510

512

2439

4994

645

Итого в 5 –м интервале

10051

5504

1157

700 и более

9432

2975

744

3900

1684

913

Итого в 6 –м интервале

13332

4659

1657

Всего

106447

34705

8864

По каждой группе определяем средний размер прибыли, средний размер кредитных вложений и средний объем вложений в ценные бумаги. Результаты представляем в итоговой таблице:

Группа

Число

банков

Кредитные вложения

Объем вложений в ценные бумаги

Прибыль

Средний размер кредитных вложений

Средний объем вложений в ценные бумаги

Средний размер прибыли

1

5

7824

2085

208

1564,8

417

41,6

2

5

20954

8934

775

4190,8

1786,8

155

3

9

32869

7049

2362

3652,1

783,22

262,44

4

7

21417

6474

2705

3059,6

924,86

386,43

5

2

10051

5504

1157

5025,5

2752

578,5

6

2

13332

4659

1657

6666

2329,5

828,5

Всего

30

106447

34705

Итого

15686

1156,8

295,47

Вывод:

По результатам группировки нельзя заключить, что с ростом средней прибыли увеличиваются или уменьшаются средний размер кредитных вложений и средний объем вложений в ценные бумаги.

2. Мода определяется по формуле:

.

Модальным является интервал [200;300], содержащий наибольшее количество банков. Получаем модальное значение прибыли:

Медиана определяется по формуле:

Медианным интервалом является интервал [200 - 300], содержащий 30/2=15-й банк. Получаем медианное значение прибыли:

=255,56.

3. По показателю размер кредитных вложений рассчитаем общую дисперсию по правилу сложения дисперсии:

,

где - межгрупповая дисперсия;

- средняя из групповых дисперсий .

Для нахождения межгрупповой дисперсии составляем вспомогательную таблицу:

Итого оборот: 15686

Число банков ()

Средний размер кредитных вложений ()

1

5

1564,8

3933875,6

19669377,8

2

5

4190,8

412934,76

2064673,8

3

9

3652,1

10795,21

97156,89

4

7

3059,6

238729,96

1671109,72

5

2

5025,5

2182415,3

4364830,58

6

2

6666

9720676,8

19441353,7

Всего

30

3548,2

47308502,5

Получаем: = 47308502,5/30=1576950,08.

Для нахождения групповых дисперсий и общей дисперсии составляем вспомогательную таблицу:

Интервал

Кредитные вложения ()

До 100

3419

3438057,64

16701,25

545

1039992,04

9019410,45

1216

121661,44

5439312,32

1605

1616,04

3776155,79

1039

276465,64

6296251,92

Итого в 1 –м интервале

7824

4877792,8

Среднее в 1 –м интервале

1564,8

975558,56

100-200

4423

53916,84

765216,72

9035

23466273,6

30104608,45

2236

3821243,04

1721956,32

2004

4782094,24

2384656,59

3256

873851,04

85400,32

Итого во 2 –м интервале

20954

32997379

Среднее во 2 –м интервале

4190,8

6599475,8

200-300

1091

6559290,12

6037995,65

2890

580813,346

433271,12

511

9866579,01

9224786,32

1490

4674724,46

4236324,45

1764

3564963,57

3183488,59

15581

142298390

144787473,65

4318

443408,012

592540,72

5077

2030308,35

2337127,52

147

12285803,9

11568388,19

Итого в 3 –м интервале

32869

182304281

Среднее в 3 –м интервале

3652,1

20256031,2

300-500

1600

2130348,76

3795613,12

981

4320459,18

6590686,99

1742

1735994,47

3262478,85

6019

8758217,47

6104687,92

778

5205568,18

7674192,72

5398

5468248,18

3421636,72

4899

3383497,47

1824570,59

Итого в 4 –м интервале

21417

31002334

Среднее в 4 –м интервале

3059,6

4428904,8

500-700

7612

6689982,25

16514199,52

2439

6689982,25

1230398,59

Итого в 5 –м интервале

10051

13379965

Среднее в 5 –м интервале

5025,5

6689982,3

700 и более

9432

7650756

34618710,19

3900

7650756

123739,79

Итого в 6 –м интервале

13332

15301512

Среднее в 6 –м интервале

6666

7650756

Всего

106447

327171981,37

Для нахождения средней из групповых дисперсий составляем таблицу внутригрупповых дисперсий:

Группа

Число банков ()

Групповая дисперсия

1

5

975558,56

4877792,8

2

5

6599475,8

32997379

3

9

20256031,2

182304281

4

7

4428904,8

31002333,6

5

2

6689982,3

13379964,6

6

2

7650756

15301512

Всего

30

279863263

Получаем: 279863263 / 30 = 9328775,427

Общая дисперсия по правилу сложения дисперсии равна: =9328775,427+1576950,08= 10905725,51.

Рассчитаем общую дисперсию по формуле: .

По результатам таблицы получаем: 327171981,37 / 30 = 10905732,71.

Вычисляем эмпирическое корреляционное отношение по формуле: .

Получаем: =0,38

Эмпирическое корреляционное отношение равно: 0,38 и означает, что связь между кредитными вложениями и прибылью средняя.

Вывод:

Модальное значение прибыли равно 266,67 млрд. руб. и равно наиболее часто встречающемуся размеру прибыли. Медианное значение прибыли равно 255,56 млрд. руб. и означает, что половина банков имеют прибыль менее 255,56 млрд. руб. По показателю размер кредитных вложений межгрупповая дисперсия равна 1576950,08, средняя из групповых дисперсий равна 9328775,427. Общая дисперсия по правилу сложения дисперсии равна 10905725,51, что приблизительно совпадает с точным значением дисперсии (разницу можно объяснить погрешностью вычислений). Эмпирическое корреляционное отношение равно: 0,38 и означает, что связь между кредитными вложениями и прибылью средняя.

Задание 2

Имеются следующие данные по району за 1999 год (условные):

1. На начало года численность трудоспособного населения рабочего возраста составила 320 т. чел., работающих лиц пенсионного возраста - 15 т. чел., работающих подростков до 16 лет - 5 т. чел.

2. В течение года вступило в рабочий возраст 20 т. чел., 0,5 т. чел. из них нетрудоспособны; прибыло из других районов трудоспособных лиц 2,5 тыс. человек. Выбыло по естественным причинам 15 тыс. чел.; в другие районы - 10 т. чел. трудоспособного населения.

Определите:

1. Численность трудовых ресурсов на начало и конец года.

2. Абсолютные и относительные показатели воспроизводства трудовых ресурсов.

Решение

1. Найдем численность трудовых ресурсов: на начало года: 320 +15 + 5 = 340 тыс. чел.

Численность трудовых ресурсов: на конец года: 340 + (20-0,5) +2,5 -15-10= 335

2. Абсолютный прирост трудовых ресурсов: 335 – 340 = -5 тыс. чел.

Численность трудовых ресурсов уменьшилась на 5 тыс. чел.

Темп роста трудовых ресурсов: 335 / 340 *100 = 98,2%.

Темп прироста трудовых ресурсов: 98,2 - 100 = -1,8%.

Численность трудовых ресурсов уменьшилась на 1,8%.

Задание 3

Имеются следующие данные по предприятию:

Номер цеха

Затраты на производство продукции, тыс. р.

Изменение себестоимости единицы продукции в отчетном периоде по сравнению с базизным, %

1

1200

+5,0

2

1800

-3,5

3

2800

-3,0

4

2500

-

Определите в целом по предприятию:

1 Изменение себестоимости единицы продукции.

2 Изменение общих затрат на производство продукции, если физический объем производства увеличился на 8 %.

3. Сумму экономии в связи с изменением себестоимости единицы продукции.

Решение

1. По условию известен индивидуальный индекс себестоимости:

_.

Найдем изменение себестоимости единицы продукции, используя общий индекс себестоимости продукции:

Номер цеха

Затраты на производство продукции, тыс. р. z₁q₁

Индивидуальный индекс себестоимости

1

1200

1,05

1142,86

2

1800

0,965

1865,28

3

2800

0,97

2886,60

4

2500

1

2500,00

Сумма

8300

8394,74

Получаем общий индекс себестоимости продукции: _{Ix = 8300 / 8394.74 = 0.989}

В целом себестоимость уменьшилась на 1.1%.

2. Если физический объем производства увеличился на 8%, то индекс физического объема равен = 1,08. Тогда общий индекс затрат на производство равен = 0,989*1,08=1.068. Следовательно, общие затраты на производство продукции увеличились на 6,81%.

3.Сумма экономии от среднего снижения себестоимости равна 8394,74-8300=94 тыс. руб.

Ответ. 1. В целом себестоимость уменьшилась на 1,1%.

2. Если физический объем производства увеличился на 8%, то общие затраты на производство продукции увеличились на 6,81%.

3.Сумма экономии от среднего снижения себестоимости равна 94 тыс. руб.

Задание 4

Имеются следующие данные по 3 рынкам города о продаже яблок:

Номер рынка

Продано яблок, тыс.р.

Цена 1 кг яблок, р.

июнь

август

июнь

август

1

2500

3000

35

30

2

1000

1200

32

25

3

1600

2000

34

30

Определите изменение средней цены на яблоки по 3 рынкам города всего и в т.ч. за счет:

- изменения цены на каждом рынке города;

- изменения, структуры продаж.

Решение

Составляем расчетную таблицу:

Номер рынка

Продано яблок, тыс.р.

Цена 1 кг яблок, р.

Продано яблок, тыс. кг

р₀q₁

июнь

р₀q₀

август р₁q₁

июнь р₀

август

р₁

июнь

q₀

август

q₁

1

2500

3000

35

30

71,429

100,000

3500

2

1000

1200

32

25

31,250

48,000

1536

3

1600

2000

34

30

47,059

66,667

2266,7

Сумма

5100

6200

149,737

214,667

7302,7

Индекс цен переменного состава:

В целом цена уменьшилась на 15,2 % , т.е. на 34,060-28,882=5,178 руб.

Индекс цен постоянного состава:

Средняя цена уменьшилась на 15,1 % из-за изменения цен на каждом рынке города, т.е на 34,060*0,151=5,143 руб.

Индекс структурных сдвигов в объеме продажи:

Из-за структурных изменений цена уменьшилась на 0,01 % т.е на 34,060*0,01= 0,341 руб.

Вывод.

В целом цена уменьшилась на 5,178 руб., т.е. на 15,2 %.

Средняя цена уменьшилась на 5,143 руб. из-за изменения цен на каждом рынке города, т.е на 15,1 %.

Из-за структурных изменений цена уменьшилась на 0,341 руб. т.е на 0,01 %.

Задание 5

Имеются следующие данные об изменении физического объема ВВП за период с 1990 г. (1990=100%):

Показатели

1991

1992

1993

1994

1995

Индекс физического объема

95,0

81,2

74,2

64,7

62,2

Определите, как в среднем ежегодно изменяется физический объем ВВП в указанном периоде. Исчислите цепные темпы изменения ВВП (в сопоставимых ценах).

Решение

В условии задачи даны базисные темпы изменения физического объема ВВП

Т_рбi= (у_i / y₀ ) *100.

Среднее ежегодное изменение физического объема ВВП равно

В среднем ежегодно физический объем ВВП в указанном периоде уменьшается на 9,1%. Так как цепные темпы изменения вычисляются по формуле: Т_рцi= (у_i / y_i-1 )*100, то цепные темпы изменения можно вычислить по формуле:

Т_рцi = Т_рбi / Т_рбi-1 *100.

Результаты вычислений представляем в таблице:

Показатели

1991

1992

1993

1994

1995

Индекс физического объема

95

85,474

91,379

87,197

96,136

Цепные темпы изменения ВВП

95

85,474

91,379

87,197

96,136

Задание 6

Имеются следующие данные о грузообороте предприятий транспорта и перевозке грузов предприятиями транспорта за 1986-1997 гг. в одном из регионов:

Годы

Грузооборот предприятий транспорта, млрд ткм

Перевозка грузов предприятиями транспорта, млн.т.

1986

280

285

1987

304

283

1988

270

321

1989

305

302

1990

301

316

1991

307

359

1992

296

334

1993

299

348

1994

296

333

1995

269

358

1996

310

305

1997

286

297

Для изучения связи между этими рядами произведите:

1. выравнивание рядов динамики по уравнению прямой;

2. вычислите коэффициент корреляции;

3. рассчитайте прогнозные значения грузооборота на 3 года вперед.

Сделайте выводы.

Решение

1. Воспользуемся прямолинейной формой связи регрессии, y = аt + b..

Оценки а и b можно искать по следующим формулам: , где - номер года и .

Для грузооборота предприятий транспорта составляем расчетную таблицу:

Годы

Грузооборот предприятий транспорта, у

1986

-11

280

121

-3080

1987

-9

304

81

-2736

1988

-7

270

49

-1890

1989

-5

305

25

-1525

1990

-3

301

9

-903

1991

-1

307

1

-307

1992

1

296

1

296

1993

3

299

9

897

1994

5

296

25

1480

1995

7

269

49

1883

1996

9

310

81

2790

1997

11

286

121

3146

Итого

0

3523

572

51

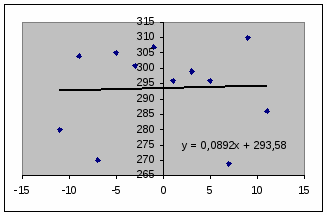
Подставляя итоги в формулы, получаем: а = 51/572=0,989, b = 3523/12=293,583

Уравнение регрессии: y = 0.989 t +293,583.

Найденное уравнение регрессии есть уравнение прямой, которая изображена на рис.

Для перевозки грузов предприятиями транспорта составляем расчетную таблицу:

Годы

Перевозка грузов предприятиями транспорта, млн.т.

1986

-11

285

121

-3135

1987

-9

283

81

-2547

1988

-7

321

49

-2247

1989

-5

302

25

-1510

1990

-3

316

9

-948

1991

-1

359

1

-359

1992

1

334

1

334

1993

3

348

9

1044

1994

5

333

25

1665

1995

7

358

49

2506

1996

9

305

81

2745

1997

11

297

121

3267

Итого

0

3841

572

815

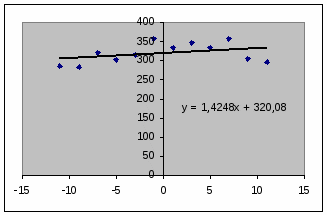
Подставляя итоги в формулы, получаем: а = 815/572=1,425, b = 3841/12=320,08

Уравнение регрессии: y = 1,425 t +320,08.

Найденное уравнение регрессии есть уравнение прямой, которая изображена на рис.

2. Вычисляем коэффициент корреляции по формуле:

, где , .

Составляем расчетную таблицу:

Годы

Исходные данные

Расчетные данные

Грузооборот предприятий транспорта, х

Перевозка грузов предприятиями транспорта, у

Х²

Y²

XY

1986

280

285

78400

81225

79800

1987

304

283

92416

80089

86032

1988

270

321

72900

103041

86670

1989

305

302

93025

91204

92110

1990

301

316

90601

99856

95116

1991

307

359

94249

128881

110213

1992

296

334

87616

111556

98864

1993

299

348

89401

121104

104052

1994

296

333

87616

110889

98568

1995

269

358

72361

128164

96302

1996

310

305

96100

93025

94550

1997

286

297

81796

88209

84942

Итого

3523

3841

1036481

1237243

1127219

Средние

293,5833

320,0833

86373,417

103103,58

93934,917

Получаем:

Так как коэффициент корреляции близок к 0, связь между признаками слабая.

3.Рассчитаем прогнозные значения грузооборота на 3 года вперед с помощью уравнения регрессии:

y = 293,583t +0.989:

у (13) = 0.989 * 13 + 293,583 = 306,362,

у (15) = 0.989 * 15 + 293,583 = 308,328,

у (17) = 0.989 * 17 + 293,583 = 310,294.

Задание 7

Имеются следующие данные по группе предприятий района:

Пре дпри ятие

Стоимость основных производственных фондов, млн.руб.

Фондоотдача (выпуск продукции на 1 руб.основных производственных фондов), руб.

Производительность труда рабочих, тыс. руб.

Фондовооруж енность труда рабочих, тыс. руб.

1

21,0

1,2

11,0

9,5

2

12,5

1,0

7,1

7,3

3

17,4

0,9

6,8

8,4

Определите по предприятиям района среднее значение:

1. стоимости основных производственных фондов на одно предприятие;

2. фондоотдачи;

3. производительности труда;

4. фондовооруженности труда

Решение

Составляем расчетную таблицу:

Предпри ятие

Стоимость основных производственных фондов, ОФ

Фондоотдача, Фо

Производительность труда С

Фондовооруж енность труда рабочих, Фв

Выпуск В= ОФ* Фо

Количество рабочих

N=В/С

Число рабо-чих Т=ОФ / Фв

1

21

1,2

11

9,5

25,2

2,291

2,211

2

12,5

1

7,1

7,3

12,5

1,761

1,712

3

17,4

0,9

6,8

8,4

15,66

2,303

2,071

Сумма

50,9

53,36

6,354

5,994

1. Находим среднее значение стоимости основных производственных фондов на одно предприятие по формуле средней арифметической простой:

50,9/3 = 16,967 млн.руб.

2.Находим среднее значение фондоотдачи по формуле средней арифметической взвешенной:

руб.

3. Находим среднее значение производительности труда по формуле средней гармонической взвешенной: 53,36/6,354=8,397 тыс. руб.

4. Находим среднее значение фондовооруженности труда по формуле средней гармонической взвешенной: 50,9/5,994=8,491 тыс. руб.

Задание 8

С целью определения средних затрат времени при поездках на работу населением города планируется выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 мин. При среднем квадратическом отклонении 15 мин.

Решение

Ошибка выборочной средней при повторном отборе вычисляется по формуле:.

Так как Р = 0,954, то коэффициент доверия t=2.

По условию, среднее квадратическое отклонение .

Из неравенства получаем:

Таким образом, должно быть обследовано не менее 900 человек.

Задание 9

Имеются следующие данные о среднедушевых доходах и расходах на продукты питания по совокупности семей в базисном и отчетном периодах:

Показатель

Базисный период

Отчетный период

Среднедушевой доход за год, т. руб.

40

45

Расходы на продукты питания, т. руб

28

33,5

Определите коэффициент эластичности расходов на питание в зависимости от роста дохода.

Решение

Определим коэффициент эластичности расходов на питание в зависимости от роста дохода по правилу:

Коэффициент эластичности =(Процентное изменение расходов на питание)/ (Процентное изменение роста дохода)

Среднедушевой доход за год увеличился на 45/40*100-100=12,5%.

Расходы на продукты питания увеличились на 33,5/28*100-100=19,6%.

Получаем: Коэффициент эластичности = 19,6 / 12,5 = 1,568.

При росте дохода на 1% расходы на питание увеличиваются на 1,568%.

Задание 10

Номинальные среднедушевые доходы населения одного из регионов составили в текущем периоде 2500 руб., за предыдущий период - 2100 руб.; доля налоговых платежей увеличилась с 20 до 22% соответственно. Цены выросли на 25%. Как изменились реальные доходы населения.

Решение

Индекс общей суммы номинальных доходов:

Индекс налогов:

Индекс цен:

Индекс общей суммы реальных доходов: .

Реальные доходы населения уменьшились на 6,4%.

Литература

1. Гусаров В.М. Статистика: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2001.

2. Сборник задач по теории статистики: Учебное пособие/ Под ред.проф. В.В.Глинского и к.э.н., доц. Л.К. Серга. Изд.З-е.- М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.

3. Статистика: Учебное пособие/Харченко Л-П., Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г.Ионина. - Изд. 2-е, перераб. и доп. - М.: ИНФРА-М.2001.

4. Теория статистики: Учебник / Под ред. Р.А. Шмойловой,- М.-.Финансы и статистика, 2000.

5. Экономика и статистика фирм: Учебник /В.Е.Адамов, С. Д. Ильенкова, Т.П. Сиротина; под ред. С.Д. Ильенковой. - 2-е изд. - М.: Финансы и статистика, 1997.