Уфимский Государственный Авиационный Технический Университет

Кафедра Экономики предпринимательства

ОТЧЕТ

по лабораторной работе № 1

по дисциплине

Эконометрика

Выполнил:

студент группы ЭУП -332

Грачева В.Д ., Байгузина Э.Х.

Проверил:

Уфа 2010

Лабораторная работа №1

Построение и эконометрический анализ однофакторных регрессионных моделей

1 Цель работы

Приобретение практических навыков по эконометрическому анализу, моделированию и прогнозированию на основе регрессий с использованием компьютерного инструментария статистико-математической обработки данных программы Statistica при построении и анализе линейной однофакторной модели регрессии.

3 Задание на лабораторную работу

1. Провести качественный анализ целей, объекта и предмета исследования. Целью исследования является выявление количественной зависимости показателей экономического явления (процесса), которая позволит принимать обоснованные решения по управлению этим экономическим явлением (процессом). Объект и предмет исследования выбираются в соответствии с заданием. Исходные данные следует брать из официальных источников статистики – статистических сборников, публикуемых Госкомстатом.

2. Подготовка исходных данных для исследования. Занести исходные данные для проведения однофакторного регрессионного анализа в программу Statistica.

3. Определить значения описательных статистик: 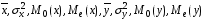по каждой переменной и объяснить их содержательный смысл.

4. Построить диаграмму рассеяния зависимой и независимой переменных. Объяснить возможные причины корреляции между этими переменными.

5. Найти значение линейного коэффициента корреляции r_xy и пояснить его смысл.

6. Построить линию регрессии и определить точечные значения оценок параметров линейного уравнения регрессии а и b и дать их интерпретацию. Какими достоинствами и недостатками с точки зрения экономической теории и практики исследуемых данных обладает построенная регрессия.

7. Определить стандартные ошибки параметров уравнения и записать доверительные интервалы для этих параметров. Сравнить точечные значения оцененных параметров с их интервальными оценками. Сделать выводы.

8. Оценить статистическую значимость параметров линейной регрессии и уравнения в целом. Все справочные данные приведены в приложениях. Сделать выводы.

9. Найти коэффициент детерминации R² и прокомментировать его значение.

10. Построить график остатков ε_i и проанализировать его.

11. Для заданного x=x_k построить точечный и интервальный (с вероятностью р=0,95) прогноз и сделать выводы.

12. Представить зависимость между исследуемыми переменными графически. Есть ли основание для использования нелинейных форм зависимостей?

13. Построить регрессии, использующие различные формы связи: обратную, показательную, экспоненциальную, логарифмическую.

14. Для каждой из рассматриваемых форм регрессий провести анализ качества уравнения регрессии. В качестве вспомогательного приема провести расчет эластичностей (там, где их значение не является очевидным из простроенных регрессий).

15. Проанализировать, улучшились ли статистические характеристики уравнения регрессии для каждой из реализованных форм регрессий (моделей) по сравнению между собой (а также по сравнению с линейной регрессионной моделью).

16. Выбрать одну из форм регрессии как наилучшую на основе нескольких критериев. Обосновать свой выбор.

17. Сделать выводы по работе.

Исходные данные

Число предприятий и организаций

17636

19023

15736

25814

13000

13014

15926

20974

17082

18486

12952

104392

11728

21628

16874

28230

23165

24121

24392

49246

21689

31617

17523

13982

16120

14385

51174

17989

61549

44602

17323

Объем промышленного производства, млн. руб.

19609

36594

24926

23011

10247

3596

6785

16161

6758

7988

6418

56443

6844

11245

13172

12881

19461

22636

16126

50927

21893

16532

13676

27638

6234

6701

28284

9199

76228

21215

14552

1)исходные данные

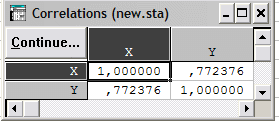
2) корреляционная матрица:

корреляционная матрица показывает, что значение коэффициента парной корреляции между переменными равно 0,77, т.е. связь между переменными функциональная.

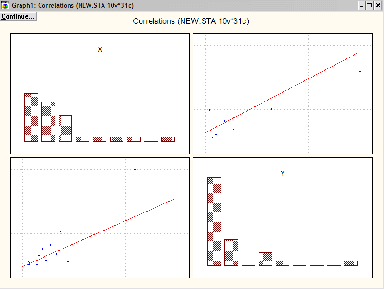
3) график зависимости результативной и факторной переменной:

Полученный график показывает, что между числом предприятий и объемами промышленного производства наблюдается сильная зависимость, т. е. можно использовать модель линейной регрессии. Над графиком дается само вычисленное уравнение линейной регрессии

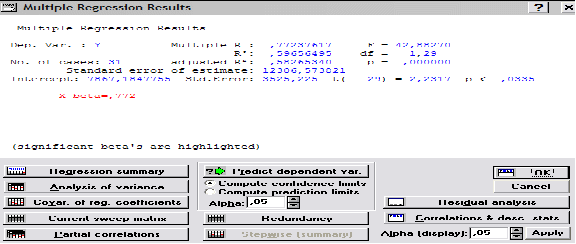
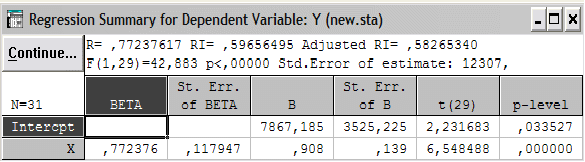
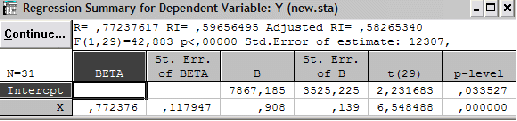
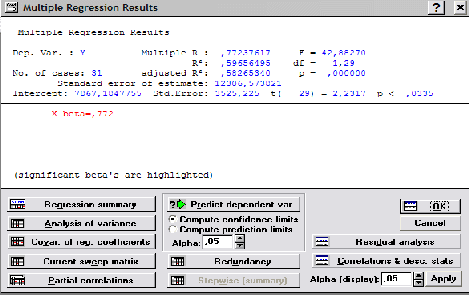
4) Анализ значимости модели и ее компонентов

• множественный коэффициент корреляции, в нашем случае равен 0,77237617

F – значение критерия Фишера, составляет 42,88270

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=19 (21 наблюдений минус 2 равно 19) при уровне значимости α=0,05 равно 0,89, а рассчитанное значение равно 42,88270. Расчетное значение значительно больше табличного, поэтому признается статистическая значимость найденного коэффициента парной корреляции между переменными.

• R² – множественный коэффициент детерминации, равен 0,59656495.

• df – число степеней свободы F-критерия, составляет 1,29.

• adjusted R² – скорректированный коэффициент детерминации, равен 0, 58265340.

• Standard error of estimate – среднеквадратическая ошибка, в примере 12306,573821.

• Intercept (Разрыв) – оценка свободного члена модели регрессии, равна –7867,1847755.

• Std.Error – стандартная ошибка оценки, составляет 3525,225.

t(29)=2,2317 и р<0,0335 – значения t-критерия и критического уровня значимости, используемые для проверки гипотезы о равенстве нулю свободного члена регрессии. в нашем случае гипотеза должна быть принята, если уровень значимости равен 0,0335 или ниже. Примем уровень значимости α = 0,05, тогда гипотеза о равенстве нулю свободного члена регрессии отклоняется.

• в 4-ом столбце В содержатся оценки параметров модели регрессии –7867,185 и 0,908

Уравнение принимает вид ОРГАН (y)= 7867.185+0.908 * выпуск(x).

• в пятом столбце St.Err. of В – значения стандартной ошибки параметров модели регрессии, соответственно 3525.225и 0,139

• в 6-ом и 7-ом столбцах t(29) и p-level – значения t-критерия и минимального уровня значимости, используемые для проверки гипотез о равенстве 0 коэффициентов регрессии. В данном примере р-значения близки к нулю, т.е. оба параметра модели значимы. Расчетные значения t-критерия Стьюдента для каждого параметра, отраженные в столбце t(29), сравниваем с табличным значением t-критерия для числа степеней свобода, равного 19. t_табл = 2,231683 при уровне значимости α=0,05. рассчитанные значения t-критерия для обоих параметров больше табличного, что свидетельствует о значимости найденных значений.

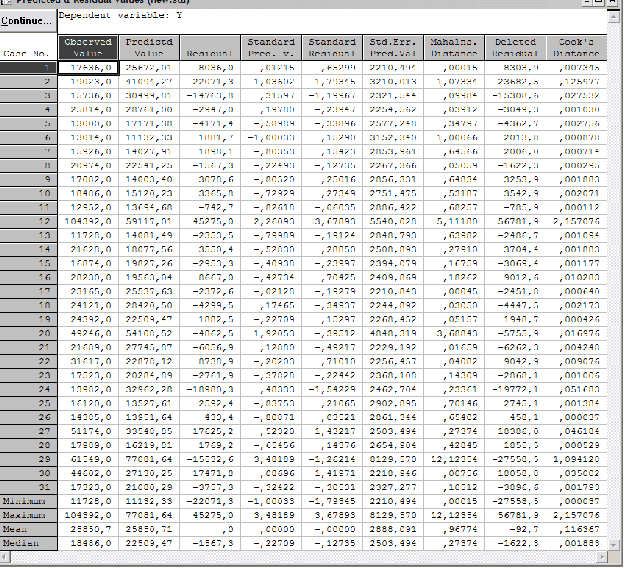
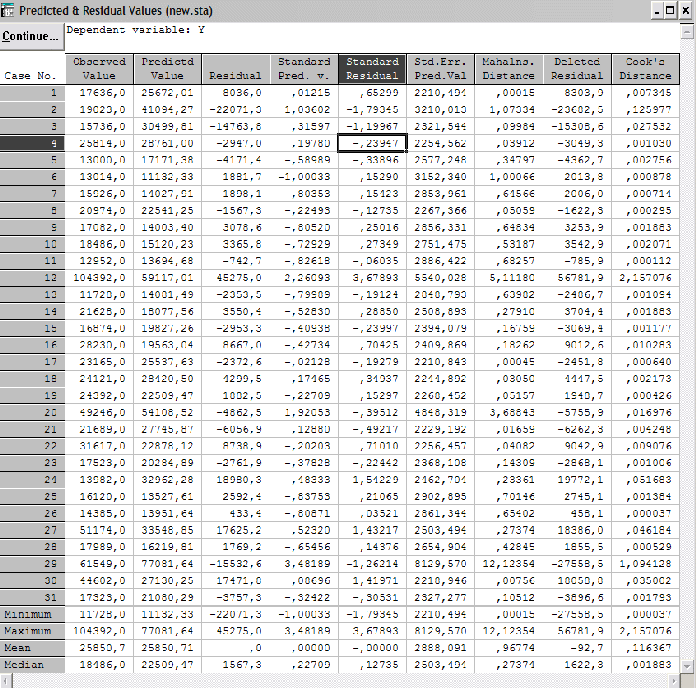
5)Анализ остатков

В нашем примере распределение остатков достаточно близко к нормальному, остатки располагаются близко к аппроксимирующей линии, что также говорит об адекватности модели.

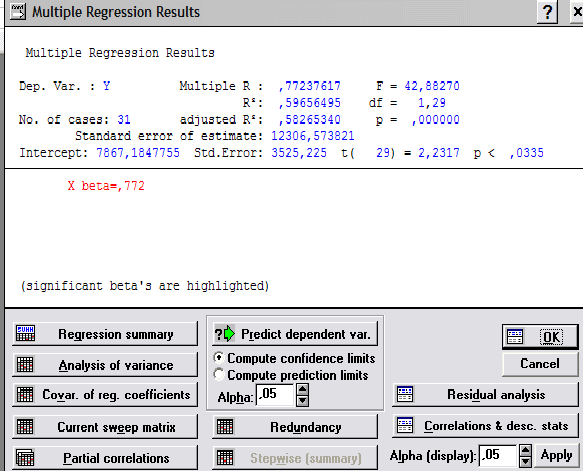
6)Построение доверительных интервалов

• Dep. Var. (Подчиненный) – имя зависимой переменной, в примере – ОРГАНИЗАЦИИ.

• Multiple R (Умножение R) – множественный коэффициент корреляции, в нашем случае равен 0,77237617.

• F – значение критерия Фишера, составляет 42,88270.

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=19 (21 наблюдений минус 2 равно 19) при уровне значимости α=0,05 равно 0,89, а рассчитанное значение равно 42,88270. Расчетное значение значительно больше табличного, поэтому признается статистическая значимость найденного коэффициента парной корреляции между переменными. Как правило, считается, что уравнение пригодно для практического использования, если F_расч > F_табл минимум в 4 раза. В нашем случае это условие соблюдается.

• R² – множественный коэффициент детерминации, равен 0,59656495.

• df – число степеней свободы F-критерия, составляет 1,29.

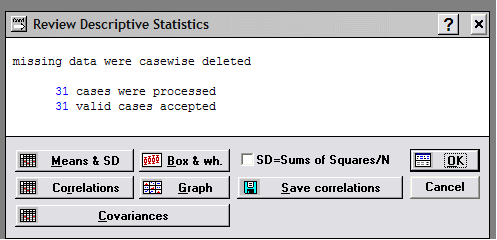
• No. of cases (Число случаев) – количество наблюдений, равно 31.

• adjusted R² – скорректированный коэффициент детерминации, равен 12306,57.

• р – критический уровень значимости модели, в примере р = 0,000000 показывает, что зависимость числа предприятий и организаций области от численности населения значима.

• Standard error of estimate – среднеквадратическая ошибка, в примере 12306,57

• Intercept (Разрыв) – оценка свободного члена модели регрессии, равна –7867,18

• Std.Error – стандартная ошибка оценки, составляет 3525,225

t(29)=2,2 и р<0,0335 – значения t-критерия и критического уровня значимости, используемые для проверки гипотезы о равенстве нулю свободного члена регрессии. в нашем случае гипотеза должна быть принята, если уровень значимости равен 0,0335 или ниже. Примем уровень значимости α = 0,05 тогда гипотеза о равенстве нулю свободного члена регрессии отклоняется.

Для вывода оценок всех коэффициентов модели регрессии и результатов проверки их значимости

• в 4-ом столбце В содержатся оценки параметров модели регрессии –7867,185и 0,139.

Уравнение принимает вид ОРГАН[y]=7867,185+0,139 * выпуск[x].

• в пятом столбце St.Err. of В – значения стандартной ошибки параметров модели регрессии, соответственно 3525,225 и 0,139

• в 6-ом и 7-ом столбцах t(29) и p-level – значения t-критерия и минимального уровня значимости, используемые для проверки гипотез о равенстве 0 коэффициентов регрессии. В данном примере р-значения близки к нулю, т.е. оба параметра модели значимы. Расчетные значения t-критерия Стьюдента для каждого параметра, отраженные в столбце t(29), сравниваем с табличным значением t-критерия для числа степеней свобода, равного 19. t_табл = 0,89 при уровне значимости α=0,05. рассчитанные значения t-критерия для обоих параметров больше табличного, что свидетельствует о значимости найденных значений.

7)Анализ остатков

В нашем примере распределение остатков достаточно близко к нормальному, остатки располагаются близко к аппроксимирующей линии, что также говорит об адекватности модели.

8)Построение доверительных интервалов

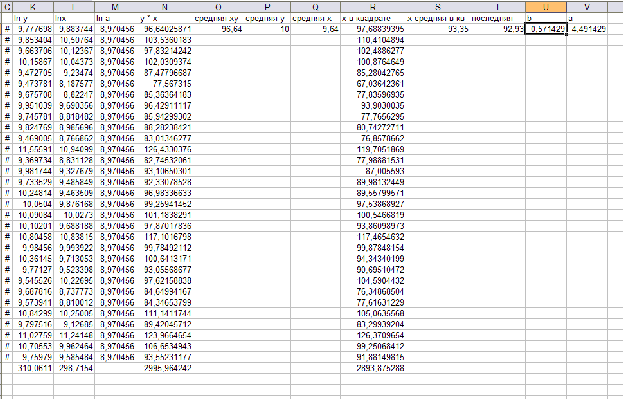
X

y

y с ^

A

1

19609

7867,185

0,908

17847,697

17636

0,012004

42,725

2

36594

7867,185

0,908

33227,352

19023

0,746694

3

24926

7867,185

0,908

22632,808

15736

0,438282

4

23011

7867,185

0,908

20893,988

25814

0,190595

5

10247

7867,185

0,908

9304,276

13000

0,284286

6

3596

7867,185

0,908

3265,168

13014

0,749103

7

6785

7867,185

0,908

6160,78

15926

0,613162

8

16161

7867,185

0,908

14674,188

20974

0,300363

9

6758

7867,185

0,908

6136,264

17082

0,640776

10

7988

7867,185

0,908

7253,104

18486

0,607643

11

6418

7867,185

0,908

5827,544

12952

0,550066

12

56443

7867,185

0,908

51250,244

104392

0,50906

13

6844

7867,185

0,908

6214,352

11728

0,470127

14

11245

7867,185

0,908

10210,46

21628

0,527905

15

13172

7867,185

0,908

11960,176

16874

0,291207

16

12881

7867,185

0,908

11695,948

28230

0,585691

17

19461

7867,185

0,908

17670,588

23165

0,237186

18

22636

7867,185

0,908

20553,488

24121

0,147901

19

16126

7867,185

0,908

14642,408

24392

0,399704

20

50927

7867,185

0,908

46241,716

49246

0,061006

21

21893

7867,185

0,908

19878,844

21689

0,08346

22

16532

7867,185

0,908

15011,056

31617

0,525222

23

13676

7867,185

0,908

12417,808

17523

0,291342

24

27638

7867,185

0,908

25095,304

13982

0,794829

25

6234

7867,185

0,908

5660,472

16120

0,648854

26

6701

7867,185

0,908

6084,508

14385

0,577024

27

28284

7867,185

0,908

25681,872

51174

0,498146

28

9199

7867,185

0,908

8352,692

17989

0,535678

29

76228

7867,185

0,908

69215,024

61549

0,124552

30

21215

7867,185

0,908

19263,22

44602

0,568109

31

14552

7867,185

0,908

13213,216

17323

0,237244

13,24722

31

100

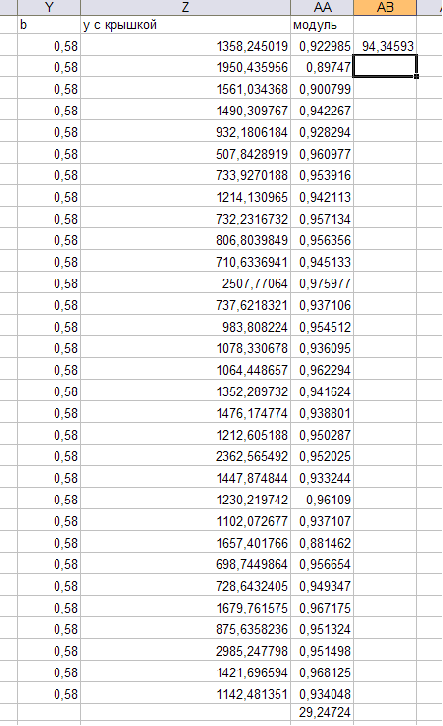
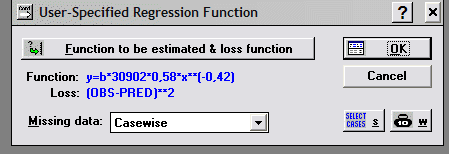
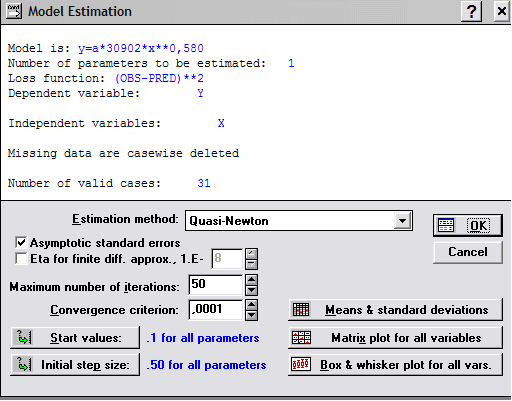
9)Нелинейные модели

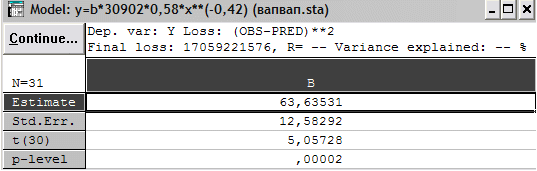
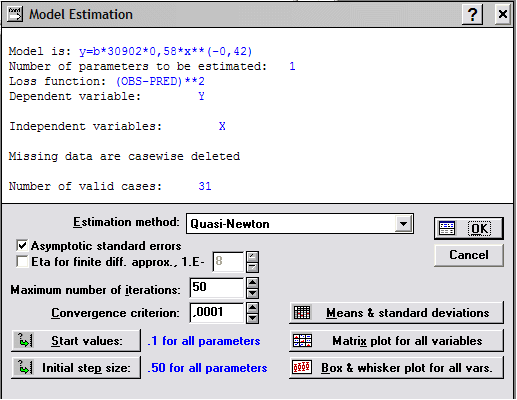
В верхнем поле этого окна отображается информация по подбору модели

• ее математическое описание,

• число искомых параметров,

• тип функции потерь,

• название переменных,

• автоматическое исключение строки при отсутствии в ней одной из переменных,

• количество обрабатываемых строк.

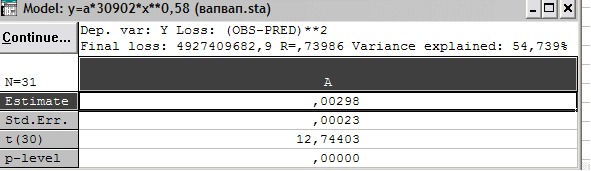
В верхнем поле отражена сумма Final loss (Конечная остаточная сумма квадратов), корреляционное отношение R и доля Variance explained (Доля объясненного рассеяния в %). Величина t (13) – t-отношение Std.Err. (Стандарт погрешности для асимптотической оценки параметра) к Estimate (Сама оценка) при 13 степенях свободы. Естественно, вероятность такого t-отношения и ошибки отклонения гипотезы о нулевой величине параметра практически равна нулю.

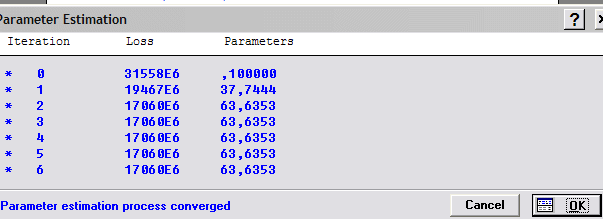
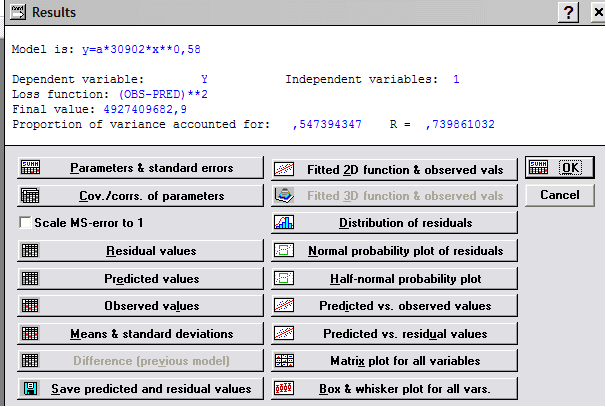
10 Вывод и анализ второго приближения зависимости

В данном случае получена большая вероятность (0,00002) ошибки отклонения гипотезы о нулевой величине второго параметра. Иными словами, эту гипотезу следует принять и оставить первое приближение.

ВЫВОД:

В линейной модели коэффициент корреляции равен 0,77. Коэффициент аппроксимации равен 42,725 .В нелинейной коэффициент аппроксимации - 94,35

Следовательно, величина отклонения теоретического значения от эмпирического в первой модели меньше ,чем во второй и наиболее оптимальной для выбора модели является первая модель, так как статистические характеристики ее уравнения регрессии для каждой из реализованных форм регрессий наиболее подходящие.