Практическое применение статистических методов
Имеются следующие данные 25 предприятий легкой промышленности по величине балансовой прибыли и объему произведенной продукции:
Таблица 1.1
№ предприятия
Объем произведенной продукции, млн. руб.
Валовая прибыль, млн. руб.
1
653
45
2
305
11
3
508
33
4
482
27
5
766
55
6
800
64
7
343
14
8
545
37
9
603
41
10
798
59
11
474
28
12
642
43
13
402
23
14
552
35
15
732
54
16
412
26
17
798
58
18
501
30
19
602
41
20
558
36
21
308
12
22
700
50
23
496
29
24
577
38
25
688
49
С целью изучения зависимости между объемом произведенной продукции и валовой прибылью произведите группировку предприятий по объему произведенной продукции (факторный признак), образовав пять групп предприятий с равными интервалами.
По каждой группе и совокупности предприятий подсчитайте:
число предприятий;
объем произведенной продукции – всего и в среднем на одно предприятие;
валовую прибыль – всего и в среднем на одно предприятие.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Решение:
1. Произведем группировку предприятий по объему произведенной продукции (факторный признак), образовав пять групп предприятий с равными интервалами.
Определим размах вариации: R = Xmax- Xmin = 800-305 = 495
Длина интервала:
Группировку произведем в таблице 1.2.
Таблица 1.2
№ п/п
Группы
№ банка
Объем произведенной продукции, млн. руб.
Валовая прибыль, млн. руб.
средний
средняя
1
305-404
2
305
339,5
11
15
21
308
12
7
343
14
13
402
23
Итого:
4
1358
60
2
405-503
16
412
473,0
26
28
11
474
28
4
482
27
23
496
29
18
501
30
Итого:
5
2365
140
3
504-602
3
508
557,0
33
36,667
8
545
37
14
552
35
20
558
36
24
577
38
19
602
41
Итого:
6
3342
220
4
603-701
9
603
657,2
41
45,6
12
642
43
1
653
45
25
688
49
22
700
50
Итого:
5
3286
228
5
702-800
15
732
778,8
54
58
5
766
55
10
798
59
17
798
58
6
800
64
Итого:
5
3894
290
Всего:
25
14245
938
Выводы:
Разбив на 5 групп по объему произведенной продукции банки получили, что:
Самая многочисленная группа 3, с количеством входящих в неё шести банков, самая малочисленная – 1, в неё входит 4 банка.
По объему произведенной продукции в общем и среднем, валовой прибыли и средней валовой прибыли на одно предприятие лидирует пятая группа, а первая – наименее эффективна.
Данные показывают, что при увеличении объема произведенной продукции валовая прибыль увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость.
Задача № 2
Имеются следующие данные по двум заводам, вырабатывающим однородную продукцию:
Таблица 2.1
Номер завода
Январь
Февраль
затраты времени на единицу продукции, час
изготовлено продукции, шт
затраты времени на
единицу продукции, час
всю продукцию, час
1
2
160
1,8
420
2
2,8
180
2,4
440
Вычислите средние затраты времени на изготовление единицы продукции по двум заводам в январе и феврале. Укажите виды средних величин, используемых в решении задач.
Решение:
Для января статистические данные представлены количеством выпущенной продукции и затратами времени на выпуск единицы продукции, поэтому средние затраты времени на изготовление единицы продукции определяем по формуле средней арифметической взвешенной:
= ,
где х - затраты времени на единицу продукции, час.
f - изготовлено продукции, шт.
= час.
Для февраля статистические данные представлены затратами времени на весь выпуск продукции и затратами времени на выпуск единицы продукции, поэтому средние затраты времени на изготовление единицы продукции определяем по формуле средней гармонической взвешенной:
= ,
где w – объем признака, равный произведению вариант на частоты: w = x f.
=
На заводе №1 в январе затраты времени на единицу продукции были снижены с 2 до 1,8 часа. На заводе №2 в 1993 г. затраты времени на единицу продукции были снижены с 2,8 до 2,4 часа.
В среднем по двум заводам затраты времени снизились с 2,424 до 2,0,64 часа, что практически обусловлено снижением эффективности производства на заводах.
Задача № 3
В целях изучения стажа рабочих одного из цехов завода проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
Таблица 3.1
Стаж рабочих, лет
Число рабочих, чел
До 5
От 5 до 10
От 10 до 15
От 15 до 20
От 20 до 25
Свыше 25
5
10
35
25
15
10
Итого
100
На основании этих данных вычислите:
Средний стаж рабочих цеха.
Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.
Коэффициент вариации.
С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.
С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.
Сделайте выводы.
Решение:
Для вычисления средней величины в каждой группе определяем серединное значение (середину интервала), после чего определяем средний стаж рабочих цеха по формуле средней арифметической взвешенной.
В закрытом интервале серединное значение определяем как полусумму верхней и нижней границ, открытые интервалы приравниваются к рядом стоящим. Кроме того, для расчёта дисперсии последовательно определяем отклонение каждой группы от средней, квадрат отклонения и произведение квадрата отклонения на число работников в группе. Расчёт производим в таблице 3.2.
Таблица 3.2
Расчет среднего квадратического отклонения
Стаж рабочих, лет
Число рабочих, чел. f
х
xf
()2
()2 f
До 5
5
2,5
12,5
-13,25
175,563
877,813
5-10
10
7,5
75
-8,25
68,0625
680,625
10-15
35
12,5
437,5
-3,25
10,5625
369,688
15-20
25
17,5
437,5
1,75
3,0625
76,5625
20-25
15
22,5
337,5
6,75
45,5625
683,438
св. 25
10
27,5
275
11,75
138,063
1380,63
Итого:
100
-
1575
-
-
4068,75
Определим средний стаж рабочих цеха:
= = = 15,75 лет.
Определим среднее квадратическое отклонение:
σ = = 6,379 лет.
Дисперсия признака σ2 = = 40,688 лет.
Определим коэффициент вариации
V = %
Определим с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.
Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле:
Δх = t
При =3μ и p = w3μ степень вероятности повышается до 0,997.
Таким образом:
t = 3
σ2= 40,688 - дисперсия признака;
n = 15,75 - средний стаж рабочих цеха;
- это 10%-ная механическая выборка.
Δх = t
Доверительные интервалы для средней будут равны:
– Δх + Δх .
=15,75 лет.4,574 года. или 15,75-4,5715,75+4,57
С вероятностью 0,997 можно утверждать, что средний стаж рабочих цеха находится в пределах от 11,18 дней до 20,32 дней.
Определим с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.
Средняя ошибки для выборочной доли при бесповторном способе отбора рассчитывается по формуле:
Δw = t .
При =3μ и p = w3μ степень вероятности повышается до 0,997.
Таким образом:
t = 3;
n = 100 - численность рабочих цеха;
- это 10%-ная механическая выборка;
Определим w - удельный вес числа рабочих со стажем работы от 10 до 20 лет.
25+35=0,6 или 60%,
100
т.е. доля рабочих со стажем работы от 10 до 20 лет – 60%.
Δw = t или 13,9%.
Доверительные интервалы для доли будут равны:
p = w Δw .
p = 60% 13,9%, тогда 60% – 13,9% p 60% + 13,9%.
Доля числа рабочих со стажем работы от 10 до 20 лет будет находиться в пределах от 46,1 до 73,9% при вероятности 0,997.
Численность населения России характеризуется следующими данными:
Таблица 4.1
-
Годы
На начало года, тыс. чел
1997
2002
2003
2004
2005
2006
2007
148041
148306
147976
147502
147105
146388
145500
Для анализа численности населения России за 2002-2007 гг. определите:
Абсолютные приросты, темпы роста и темпы прироста по годам и к 2002 году.
Полученные показатели представьте в таблице.
Среднегодовую численность населения России.
Среднегодовой темп роста и прироста численности населения России за 2002-2007 гг. и за 1997-2002 гг.
Постройте график динамики численности населения России.
Сделайте выводы.
Решение:
Определим абсолютные приросты, темпы роста и темпы прироста по годам и к 2002 году. Полученные показатели представим в таблице 4.2.
Таблица 4.2
Абсолютные приросты, темпы роста и темпы прироста
Годы
На начало года, тыс. чел
уi
Абс. приросты, млн.тонн
Темпы роста
Темпы прироста, %
цепные
базисные (к 2002г)
цепные
базисные (к 2002г)
цепные
базисные (к 2002г)
yц = уi – yi-1
yб =
уi – y2002
k =
k =
Δkц =
kц % – 100
Δkб =
k % – 100
1997
148041
265
-265
1,002
0,998
0,2%
-0,2%
2002
148306
-
-
-
-
-
-
2003
147976
-330
-330
0,998
0,998
-0,2%
-0,2%
2004
147502
-474
-804
0,997
0,995
-0,3%
-0,5%
2005
147105
-397
-1201
0,997
0,992
-0,3%
-0,8%
2006
146388
-717
-1918
0,995
0,987
-0,5%
-1,3%
2007
145500
-888
-2806
0,994
0,981
-0,6%
-1,9%
2. Определим среднегодовую численность населения России за 2002-2007 гг.:
За 2002-2007 гг. мы имеем интервальный ряд динамики с равными интервалами. Поэтому среднегодовую численность населения исчислим по формуле средней арифметической простой:
====
147129,5тыс.чел.
где у – уровни ряда
n – число уровней ряда.
3. Среднегодовой темп роста и прироста численности населения России за 2002-2007 гг.
Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
==,
где n – число цепных темпов роста;
за 2002-2007 гг.: ===0,996 или 99,6%.
Среднегодовой темп роста численности населения России за 2002-2007 гг. равен 99,6 %.
Среднегодовой темп прироста за 2002-2007 гг. исчисляется следующим образом:
Δ = % – 100%=99,6–100=0,4%.
Таким образом, численность населения России за период 2002-2007 гг. уменьшалось за год в среднем на 0,4%.
Выводы: численность населения России по данным таблицы 4.1. в 2002 году повысилась по сравнению с 1997 годом на 265 тыс.чел. или на 0,2%. Затем вплоть до 2007 года снижалось в среднем на 0,4% за год.
Имеются следующие данные о стоимости имущества предприятия (млн. руб.):
Таблица 5.1
01.01.
01.02.
01.03.
01.04.
01.05.
01.06.
01.07.
Стоимость имущества, млн. руб.
62
68
65
68
70
75
78
Определите среднегодовую стоимость имущества:
за I квартал;
за II квартал;
за полугодие в целом.
Решение:
Среднегодовая стоимость имущества рассчитывается по формуле средней арифметической простой:
За I квартал: = = 66 млн. руб.
За II квартал: = = 72,667 млн. руб.
За полугодие в целом: = = 69,333 млн. руб.
Динамика средних цен и объема продажи на колхозных рынках города характеризуется следующими данными:
Таблица 6.1
Наименование товара
Продано товаров за период, тыс. кг
Средняя цена за 1 кг за период, руб.
базисный
отчетный
базисный
отчетный
Колхозный рынок № 1:
Картофель
Свежая капуста
6,0
2,5
6,2
2,4
8,0
15,0
8,5
19,0
Колхозный рынок №2:
Картофель
12,0
12,8
7,5
8,0
На основании имеющихся данных вычислите:
Для колхозного рынка № 1 (по двум видам товаров вместе):
а) общий индекс товарооборота в фактических ценах;
б) общий индекс цен;
в) общий индекс физического объема товарооборота.
Определите в отчетном периоде прирост товарооборота в абсолютной сумме и разложите по факторам (за счет изменения цен и объема продаж товаров).
Покажите взаимосвязь начисленных индексов.
Для двух колхозных рынков вместе (по картофелю):
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продажи картофеля на динамику средней цены.
Решение:
1. Для колхозного рынка № 1 определим индивидуальные индексы:
По товару Картофель: ip = = = 1,033 или 103,3%,
iq = = = 1,063 или 106,3%,
По товару Свежая капуста: ip = = = 0,960 или 96%,
iq = = = 1,267 или 126,7%.
Таблица 6.2
Индивидуальные индексы для товаров колхозного рынка №1
Индивидуальные индексы
Продано товаров за период, тыс. кг
Средняя цена за 1 кг за период, руб.
Картофель
1,033
1,063
Свежая капуста
0,960
1,267
Таким образом:
цены на картофель выросли в отчетном году на 6,3%;
объем продаж по картофелю увеличился на 3,3%.
цены на свежую капусту выросли в отчетном периоде на 26,7%;
свежей капусты было продано в отчетном периоде по сравнению с базисным на 4% меньше.
а) Чтобы определить изменение товарооборота в фактических ценах в абсолютной сумме, необходимо рассчитать агрегатный индекс товарооборота в фактических ценах:
Ipq = = = = 1,150 или 115,0%.
Разность между числителем и знаменателем индекса товарооборота в фактических ценах дает прирост (или снижение) товарооборота в абсолютной сумме:
Δpq = –= 98,3-85,5 = 12,8 (тыс. руб.).
Товарооборот в фактических ценах вырос в отчетном периоде по сравнению с базисным периодом на 15% или на 12,8 тыс.руб.
б) Перейдем к расчету агрегатного индекса цен. В качестве веса введем в индекс неизменное количество товаров отчетного периода (по формуле Пааше). Формула агрегатного индекса цен будет выглядеть следующим образом:
Ip = = = = 1,148 или 114,8%.
Разность между числителем и знаменателем индекса цен дает прирост (снижение) товарооборота за счет изменения цен:
Δpq(p) = –= 98,3-85,6 =12,7 (тыс. руб.).
Прирост товарооборота в абсолютной сумме в отчетном периоде составил 12,7 тыс. рублей за счет увеличения цен на 14,8%.
в) Чтобы рассчитать агрегатный индекс физического объема товарооборота, который будет характеризовать изменение объема продажи товаров, примем в качестве веса неизменные цены базисного периода и определим стоимость каждого товара:
Iq = = = = 1,001 или 100,1%,
Разность между числителем и знаменателем индекса физического объема товарооборота дает прирост (или снижение) товарооборота в неизменных ценах:
Δpq(q) = –= 85,6-85,5 = 0,1 (тыс. руб.).
Прирост товарооборота в абсолютной сумме в отчетном периоде за счет увеличения количества проданного товара на 0,1% составил 0,1 тыс. руб.
Связь между изменениями объема товарооборота, количеством продажи товаров и уровнем их цен выражается в системе взаимосвязанных индексов:
= или = Ipq ,
тогда в нашем примере:
1,148*1,001=1,150
Произведение двух индексов () дает нам показатель динамики товарооборота в фактических ценах (Ipq), то есть за счет роста цен на 14,8% (в абсолютной сумме – 12,7 тыс.руб.) и увеличения объема продаж на 0,1% (в абсолютной сумме – 100 руб.), товарооборот увеличился в отчетном году на 15% (в абсолютной сумме – 12,8 тыс.руб.).
2. а) Индекс цен переменного состава определим по следующей формуле:
==:
или =:==1,0648 или 106,48%.
Средняя цена единицы продукции по двум заводам возросла на 6,48%.
б) Индекс постоянного состава определим по агрегатному индексу цен:
Ip = = = = 1,0652 или 106,52%.
Это означает, что в среднем по двум заводам цена единицы повысилась на 6,52%.
в) Индекс структурных сдвигов определим по формуле:
Iстр = :
или Iстр = :==0,9995 или 99,95%
Средняя цена единицы по двум заводам снизилась на 0,05% за счет изменения удельного веса на отдельном заводе в общем выпуске продукции.
Покажем взаимосвязь трех исчисленных индексов:
= или 1,0652 = .
Общий вывод: Если бы происшедшие изменения цен продукции не сопровождались перераспределениями в ее выпуске, то средняя себестоимость продукции по двум заводам выросла бы на 6,48%.
Изменение структуры выпуска продукции в общем объеме вызвало снижение цен на 0,05%. Одновременное воздействие двух факторов увеличило среднюю цену продукции по двум заводам на 6,52%.
группировка средний прирост дисперсия
По заводу имеются следующие данные о выпуске продукции:
Таблица 7.1
Вид продукции
Выпуск продукции в I квартале, тыс. руб.
Увеличение (+) или уменьшение (-) выпуска продукции во II квартале по сравнению с I кварталом, %
Рельсы трамвайные
22300
+3,0
Чугун литейный
15800
-2,0
Железо листовое
10500
+1,5
1.Определить общий индекс физического объема продукции.
2.Определить сумму изменения затрат за счет объема произведенной продукции.
Решение:
1. Определим индивидуальные индексы физического объема товарооборота в таблице:
Таблица 7.2
Вид продукции
Выпуск продукции в I квартале, тыс. руб.
Индивидуальный индекс физического объема, т/об
Рельсы трамвайные
22300
1,03
Чугун литейный
15800
0,98
Железо листовое
10500
1,015
q = = = = 1,011
Физический объем продукции увеличился на 1,1%.
2. Сумма изменения затрат равна 49110,5-48600 = 510,5 тыс.руб.
Таким образом за счет увеличения физического объема продукции на 1,1% сумма затрат увеличилась на 510,5 тыс.руб.
Для изучения тесноты связи между объемом произведенной продукции (факторный признак – Х) и балансовой прибылью (результативный признак – У) по данным задачи № 1 вычислите эмпирическое корреляционное отношение.
Сделайте выводы.
Решение:
Для расчета межгрупповой дисперсии строим расчетную таблицу 8.1.
Таблица 8.1
Расчет среднего квадратического отклонения
Группы банков по объему произведенной продукции
Число банков
n
Сумма прибыли на один банк, млн.руб. У
()2
()2n
305-404
4
15,00
-22,520
507,150
2028,602
405-503
5
28,00
-9,520
90,630
453,152
504-602
6
36,67
-0,853
0,728
4,369
603-701
5
45,60
8,080
65,286
326,432
702-800
5
58,00
20,480
419,430
2097,152
Итого:
25
37,52
4909,707
Рассчитаем межгрупповую дисперсию по формуле
= ==196,388
Для расчета общей дисперсии возведем все значения «у» (валовую прибыль) в квадрат.
Таблица 8.2
Валовая прибыль, млн.руб.
У
Валовая прибыль, млн.руб.
У2
Валовая прибыль, млн.руб.
У
Валовая прибыль, млн.руб.
У2
Валовая прибыль, млн.руб.
У
Валовая прибыль, млн.руб.
У2
45
2025
59
3481
41
1681
11
121
28
784
36
1296
33
1089
43
1849
12
144
27
729
23
529
50
2500
55
3025
35
1225
29
841
64
4096
54
2916
38
1444
14
196
26
676
49
2401
37
1369
58
3364
ИТОГО
40362
41
1681
30
900
Рассчитаем общую дисперсию по формуле:
= – = – 37,522 = 206,73
Тогда коэффициент детерминации будет:
η2 == = 0,950.
Он означает, что вариация суммы выданных банком кредитов на 95% объясняется вариацией размера процентной ставки и на 5% – прочими факторами.

Нравится материал? Поддержи автора!
Ещё документы из категории экономика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ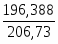
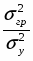
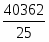
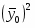

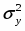
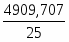
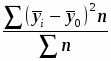
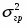
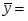
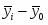
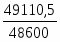
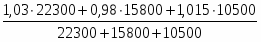
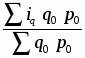
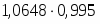
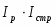
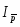
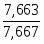
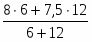
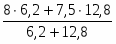
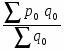
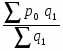
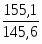
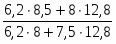
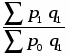
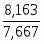
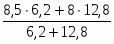
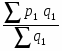
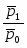
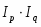
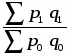
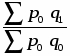
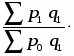
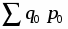
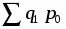
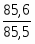
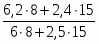
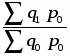
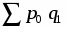
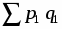
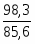
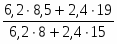
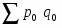
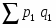
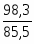
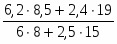
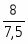
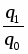
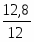
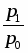
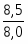
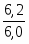
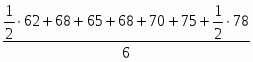
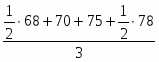
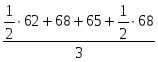
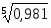
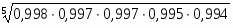
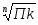
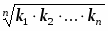
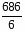

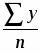
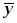
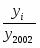


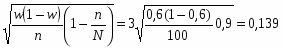
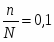
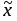
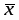
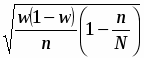
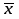
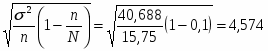
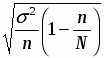
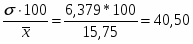
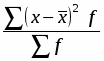
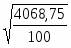
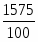
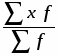
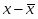
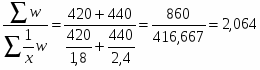
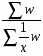
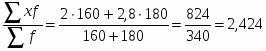
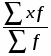
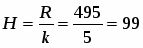 Задача № 1
Задача № 1