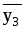
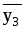
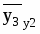
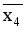
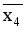
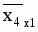
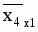
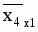
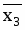
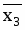
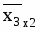
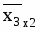
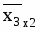
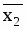
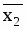
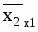
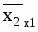
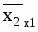
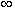
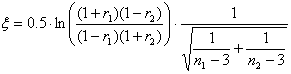
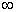
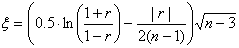
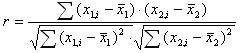
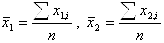
КУРСОВАЯ РАБОТА

«Расчет коэффициента корреляции между притоком прямых иностранных инвестиций и темпами экономического роста на примере Великобритании и Венгрии

Содержание

Введение

1. Теоретические аспекты изучения корреляционных связей в экономике

1.1 Корреляционный анализ

1.2 Краткая экономическая характеристика Великобритании

1.3 Краткая экономическая характеристика Венгрии

2. Корреляционный анализ экономики

2.1 Анализ основных показателей прироста иностранных инвестиций

2.2 Анализ корреляционных связей и темпов экономического роста

Заключение

Список литературы

Введение

Актуальность темы данной работы определяется тем, что обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности.

Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных.

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи показателей биржевых ставок методами корреляционно-регрессионного анализа.

Цель работы определить коэффициент корреляции между притоками ПИИ и темпами экономического роста развитой и развивающейся страны

В связи с поставленной целью необходимо решить ряд задач:

– дать понятие корреляционному анализу

– дать характеристику экономики Великобритании

– дать характеристику экономики Венгрии

– Провести анализ между прямыми иностранными инвестициями и ростом ВВП страны

1. Теоретические аспекты изучения корреляционных связей в экономике

1.1 Корреляционный анализ

Корреляционный анализ – метод, позволяющий обнаружить зависимость между несколькими случайными величинами.

Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию – о взаимосвязи этих параметров.

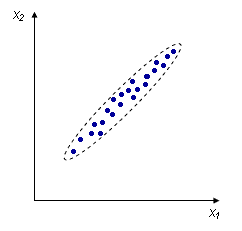
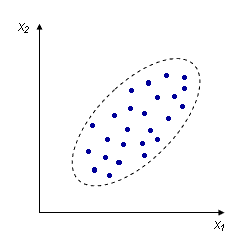
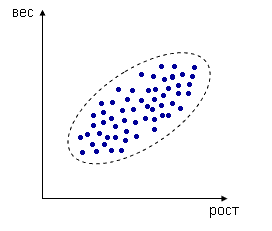
Например, измеряем рос и вес человека, каждое измерение представлено точкой в двумерном пространстве:

Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость – корреляция.

В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:

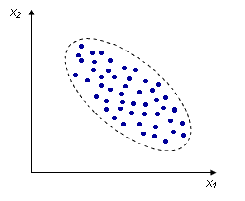
Отрицательная корреляция:

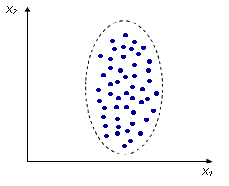
Отсутствие корреляции:

Корреляцию необходимо охарактеризовать численно, чтобы, например, различать такие случаи:

Для этого вводится коэффициент корреляции. Он рассчитывается следующим образом:

Есть массив из n точек {x1, i, x2, i}

Рассчитываются средние значения для каждого параметра:

И коэффициент корреляции:

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна.

Коэффициент корреляции является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:

1. Коэффициент корреляции значимо отличается от нуля (т.е. корреляция есть):

Тестовая статистика вычисляется по формуле:

и сравнивается с табличным значением коэффициента Стьюдента t (p = 0.95, f = ) = 1.96

Если тестовая статистика больше табличного значения, то коэффициент значимо отличается от нуля. По формуле видно, что чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля)

2. Отличие между двумя коэффициентами корреляции значимо:

Тестовая статистика:

Также сравнивается с табличным значением t (p,)

Методами корреляционного анализа решаются следующие задачи:

1) Взаимосвязь. Есть ли взаимосвязь между параметрами?

2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.

3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.

1.2 Краткая экономическая характеристика Великобритании

Великобритания – высокоразвитая индустриальная страна, входит в первую пятерку наиболее развитых государств мира. По запасам энергоресурсов Великобритания занимает 1-е место в Европе и является крупным производителем нефти и газа

Главной особенностью макроэкономического развития страны является то, что Великобритания выбрала неолиберальную, «англосаксонскую» модель развития. Для нее характерно преобладание свободного частного предпринимательства (более 80% общего объема производства). Частный сектор обеспечивает свыше 75% всех рабочих мест. Политика британского правительства направлена на создание максимально благоприятных возможностей для развития частного бизнеса. Однако при общем повышении жизненного уровня населения в стране наблюдается значительная поляризация доходов, когда 10% населения владеют 54% национального богатства.

Великобритания в международном разделении труда выступает как поставщик промышленной продукции. Вместе с тем экономическая роль Великобритании в современном мире определяется не только промышленной, но и банковской, страховой, судо-фрахтовой и другой коммерческой деятельностью. Около 30% ее валового национального продукта поступает от обрабатывающей промышленности и 45% – от сферы обслуживания, включающей транспорт и связь, розничную торговлю, страхование, банки и другие финансовые учреждения, здравоохранение и образование. Доля сферы обслуживания в валовом национальном продукте увеличивается значительно быстрее, чем доля обрабатывающей промышленности, которая даже несколько снижается. Уменьшилась также доля сельского хозяйства – до 3% и добывающей промышленности – до 1,4%.

Вывоз промышленных товаров и экспорт «услуг» для развития экономики Великобритании имеет исключительное значение, которые вместе дают 26% валового национального продукта. Важной статьей дохода британских международных монополий был и остается вывоз капитала в другие страны.

С переориентацией британской промышленности на новейшие отрасли для ее развития внешний рынок стал играть большую роль, чем дешевая рабочая сила. В последнее время этот рынок британские монополии находят в развитых капиталистических странах, доля которых в вывозе британского капитала превысила 3/5. Все еще велик экспорт капитала Великобритании в развивающиеся страны: на нее приходится почти половина капитала вывозимого в эти страны западноевропейскими государствами. В то же время быстро растут вклады иностранных монополий в экономику Великобритании.

Великобритания, потеряв почти все свои колонии, утратила многие экономические преимущества: контроль над богатейшими мировыми месторождениями – цветных металлов, нефти, важными источниками натурального каучука, дешевой сельскохозяйственной продукции, гарантированные рынки сбыта промышленных товаров и безграничные возможности вывоза капитала на все континенты.

Будучи должником США и их «младшим» партнером и взяв на себя значительные расходы по НАТО, Великобритания вынуждена мириться с проникновением в ее экономику американского капитала, роль которого возрастает с каждым годом. Деньги магнатов из-за океана вкладываются преимущественно в быстро развивающиеся современные отрасли промышленности. Американскими фирмами выпускается свыше половины автомобилей, 3/5 ЭВМ и такая же доля медикаментов. Более половины компаний, занятых разведкой месторождений нефти и газа в Северном море – также американские.

1.3 Краткая экономическая характеристика Венгрии

Венгрия – новая постсоциалистическая страна Центральной Европы с экономикой, в которой уже утвердились основные рыночные принципы. Современный уровень экономического и социального развития Венгрии эксперты считают одним из самых высоких среди стран Центральной и Юго-Восточной Европы. Венгерская экономика в значительной мере ориентирована на Европейский Союз. Благоприятная в начале 2000 г. конъюнктура в странах ЕС способствовала ускоренному экономическому росту и в Венгрии: в I квартале ВВП возрос на 6,6% по сравнению с аналогичным периодом 1999 г. Наметившееся к концу 2000 г. замедление темпов экономического роста в Евросоюзе сыграло определяющую роль в снижении темпов роста и в Венгрии.

Тем не менее, в целом за 2000 г. Венгрии удалось сохранить за собой одно из лидирующих мест среди стран региона по темпам экономического роста (5,3% при среднем темпе прироста по странам Центральной Европы порядка 4,2%).

Форсированный приток иностранного капитала привел к коренной перестройке структуры венгерской экономики. В Венгрии за последние годы сформировалась индустриально-аграрная структура экономики западноевропейского типа: промышленность и строительство обеспечивают более 30% произведенного ВВП, сельское хозяйство – около 5%, а сфера услуг – 65%.

Довольно прочным и устойчивым представляется нынешнее валютно-финансовое положение Венгрии. Несмотря на значительное ухудшение для страны условий внешней торговли, в допустимых пределах удается удерживать дефицит внешнеторгового и платежного балансов страны.

Степень либерализации внешнеторгового режима, осуществленной в Венгрии, оценивается секретариатом ВТО в основном положительно, хотя отмечается сравнительно высокий средний уровень таможенных пошлин, применяемых Венгрией в рамках режима наибольшего благоприятствования.

Розничный товарооборот на внутреннем рынке после спада 1987–1997 гг. постоянно расширяется (в 2002 г. – 24,8 млн. долл.). Этому способствуют рост денежных доходов населения, появление новых видов торговли (гипермаркетов, торговых центров) и повышение качества обслуживания. Структура товарооборота приблизительно таклва: 33,4% – продовольствие, 28,4% – транспортные средства, запчасти и топливо к ним, 16,4% – мебель и бытовая техника, 9,5% – товары культурно-познавательного назначения.

В Будапеште 25 ноября 2005 г. состоялась конференция «Динамичная экономика», в ходе которой министр финансов Венгрии Я. Вереш, подводя итоги развития венгерской экономики за последние годы, отметил, что рост венгерского ВВП как по номиналу, так и по паритету покупательной способности был наивысшим среди стран региона. Устойчивый рост экспорта свидетельствует о том, что выпускаемая Венгрией продукция качественна и пользуется спросом на мировых рынках. Источниками роста венгерской экономики являются, в первую очередь, инвестиции транснациональных корпораций и государственные капиталовложения. Эра транснациональных корпораций и производства продуктов с низкой долей добавленной стоимости подошла к концу, поэтому экономическая стратегия должна меняться

2. Корреляционный анализ экономики

2.1 Анализ основных показателей прироста иностранных инвестиций

Таблица 1 Исходные данные

Годы

ВВП

Инвестиции

Население

ВВП на душу

Венгрия

Великобритания

Венгрия

Великобритания

Венгрия

Великобритания

Венгрия

Великобритания

flow

stock

flow

stock

1970

5862

91505

-14

-

-

-

13193

816341

444

112

1971

6532

98562

-3

-

-

-

13567

836575

481

118

1972

7244

112161

60

-

-

-

13951

856684

519

131

1973

8668

136769

96

-

-

-

14345

876160

604

156

1974

10929

142255

62

-

-

-

14749

894620

741

159

1975

13346

161162

81

-

-

-

15161

911807

880

177

1976

12730

151628

72

-

-

-

15582

927548

817

163

1977

11475

172349

42

-

-

-

16012

941975

717

183

1978

9851

214160

17

-

-

-

16447

955438

599

224

1979

12583

263190

37

-

-

-

16886

968388

745

272

1980

16740

306520

27

890

57

1074

17325

981235

966

312

1981

20448

293852

125

965

265

1339

17763

993977

1151

296

1982

20801

295370

48

1022

430

1769

18200

1006632

1143

293

1983

16142

317352

38

1092

916

2685

18638

1019587

866

311

1984

16923

314637

-89

1119

1419

4104

19079

1033202

887

305

1985

14610

309083

1

1130

1956

6060

19523

1047715

748

295

1986

21725

304348

22

1152

2244

8304

19972

1063348

1088

286

1987

35586

329851

32

1173

2314

10617

20422

1079915

1743

305

1988

31082

413439

26

1258

3194

13811

20872

1096826

1489

377

1989

34947

459782

59

1287

3393

17204

21320

1113313

1639

413

1990

29281

404494

41

1330

3487

20691

21762

1128790

1346

358

1991

34544

424117

-7

1370

4366

25057

22199

1143047

1556

371

1992

36083

499859

-79

1504

11008

36064

22628

1156259

1595

432

1993

34835

641069

761

1642

27515

63579

23050

1168652

1511

549

1994

44910

582653

3289

4451

33767

74151

23460

1180625

1914

494

1995

53635

756960

2557

5510

37521

101098

23857

1192464

2248

635

1996

55813

892014

3471

6720

41726

128069

24242

1204238

2302

741

1997

59130

985046

2139

7753

45257

153995

24613

1215797

2402

810

1998

56752

1045199

1644

8297

45463

175156

24973

1227016

2273

852

1999

51553

1098832

1940

9791

40319

186189

25322

1237730

2036

888

2000

53336

1192836

810

11062

40715

193348

25663

1247777

2078

956

2001

53954

1316558

1144

11835

46878

203142

25995

1257144

2076

1047

2002

57059

1454040

2156

12549

52743

216503

26321

1265938

2168

1149

2003

61504

1647918

1335

12876

53505

228371

26641

1274276

2309

1293

2004

69662

1936502

1599

13310

60360

245467

26959

1282336

2584

1510

2005

79382

2278419

2579

15889

72406

272094

27274

1290336

2911

1766

2006

90048

2666772

3467

19356

69468

292559

27589

1298049

3264

2054

Таблица 2 Темпы прироста показателей для Венгрия

Годы

Абсолютные значения

Темпы прироста

ВВП, у1

Инвестиции

Население, у4

ВВП на душу

ВВП

Инвестиции

Население

ВВП на душу

flow, у2

stock, у3

flow

stock

1970

5862

-14

-

13193

444

1971

6532

-3

-

13567

481

1,11

-

-

1,03

1,08

1972

7244

60

-

13951

519

1,11

-

-

1,03

1,08

1973

8668

96

-

14345

604

1,20

-

-

1,03

1,16

1974

10929

62

-

14749

741

1,26

-

-

1,03

1,23

1975

13346

81

-

15161

880

1,22

-

-

1,03

1,19

1976

12730

72

-

15582

817

0,95

-

-

1,03

0,93

1977

11475

42

-

16012

717

0,90

-

-

1,03

0,88

1978

9851

17

-

16447

599

0,86

-

-

1,03

0,84

1979

12583

37

-

16886

745

1,28

-

-

1,03

1,24

1980

16740

27

890

17325

966

1,33

-

-

1,03

1,30

1981

20448

125

965

17763

1151

1,22

4,63

1,08

1,03

1,19

1982

20801

48

1022

18200

1143

1,02

0,38

1,06

1,02

0,99

1983

16142

38

1092

18638

866

0,78

0,79

1,07

1,02

0,76

1984

16923

-89

1119

19079

887

1,05

-2,34

1,02

1,02

1,02

1985

14610

1

1130

19523

748

0,86

-0,01

1,01

1,02

0,84

1986

21725

22

1152

19972

1088

1,49

22,00

1,02

1,02

1,45

1987

35586

32

1173

20422

1743

1,64

1,45

1,02

1,02

1,60

1988

31082

26

1258

20872

1489

0,87

0,81

1,07

1,02

0,85

1989

34947

59

1287

21320

1639

1,12

2,27

1,02

1,02

1,10

1990

29281

41

1330

21762

1346

0,84

0,69

1,03

1,02

0,82

1991

34544

-7

1370

22199

1556

1,18

-0,17

1,03

1,02

1,16

1992

36083

-79

1504

22628

1595

1,04

11,29

1,10

1,02

1,02

1993

34835

761

1642

23050

1511

0,97

-9,63

1,09

1,02

0,95

1994

44910

3289

4451

23460

1914

1,29

4,32

2,71

1,02

1,27

1995

53635

2557

5510

23857

2248

1,19

0,78

1,24

1,02

1,17

1996

55813

3471

6720

24242

2302

1,04

1,36

1,22

1,02

1,02

1997

59130

2139

7753

24613

2402

1,06

0,62

1,15

1,02

1,04

1998

56752

1644

8297

24973

2273

0,96

0,77

1,07

1,01

0,95

1999

51553

1940

9791

25322

2036

0,91

1,18

1,18

1,01

0,90

2000

53336

810

11062

25663

2078

1,03

0,42

1,13

1,01

1,02

2001

53954

1144

11835

25995

2076

1,01

1,41

1,07

1,01

1,00

2002

57059

2156

12549

26321

2168

1,06

1,88

1,06

1,01

1,04

2003

61504

1335

12876

26641

2309

1,08

0,62

1,03

1,01

1,06

2004

69662

1599

13310

26959

2584

1,13

1,20

1,03

1,01

1,12

2005

79382

2579

15889

27274

2911

1,14

1,61

1,19

1,01

1,13

2006

90048

3467

19356

27589

3264

1,13

1,34

1,22

1,01

1,12

Средний коэффициент роста

1,08

1,21

1,13

1,02

1,06

Таблица 3 Темпы прироста показателей для Великобритании

Годы

Абсолютные значения

Темпы прироста

ВВП, у1

Инвестиции

Население, у4

ВВП на душу

ВВП

Инвестиции

Население

ВВП на душу

flow, у2

stock, у3

flow

stock

1970

91505

816341

112

1971

98562

-

-

836575

118

1,08

-

-

1,02

1,05

1972

112161

-

-

856684

131

1,14

-

-

1,02

1,11

1973

136769

-

-

876160

156

1,22

-

-

1,02

1,19

1974

142255

-

-

894620

159

1,04

-

-

1,02

1,02

1975

161162

-

-

911807

177

1,13

-

-

1,02

1,11

1976

151628

-

-

927548

163

0,94

-

-

1,02

0,92

1977

172349

-

-

941975

183

1,14

-

-

1,02

1,12

1978

214160

-

-

955438

224

1,24

-

-

1,01

1,23

1979

263190

0

-

968388

272

1,23

-

-

1,01

1,21

1980

306520

57

1074

981235

312

1,16

-

-

1,01

1,15

1981

293852

265

1339

993977

296

0,96

4,65

1,25

1,01

0,95

1982

295370

430

1769

1006632

293

1,01

1,62

1,32

1,01

0,99

1983

317352

916

2685

1019587

311

1,07

2,13

1,52

1,01

1,06

1984

314637

1419

4104

1033202

305

0,99

1,55

1,53

1,01

0,98

1985

309083

1956

6060

1047715

295

0,98

1,38

1,48

1,01

0,97

1986

304348

2244

8304

1063348

286

0,98

1,15

1,37

1,01

0,97

1987

329851

2314

10617

1079915

305

1,08

1,03

1,28

1,02

1,07

1988

413439

3194

13811

1096826

377

1,25

1,38

1,30

1,02

1,23

1989

459782

3393

17204

1113313

413

1,11

1,06

1,25

1,02

1,10

1990

404494

3487

20691

1128790

358

0,88

1,03

1,20

1,01

0,87

1991

424117

4366

25057

1143047

371

1,05

1,25

1,21

1,01

1,04

1992

499859

11008

36064

1156259

432

1,18

2,52

1,44

1,01

1,17

1993

641069

27515

63579

1168652

549

1,28

2,50

1,76

1,01

1,27

1994

582653

33767

74151

1180625

494

0,91

1,23

1,17

1,01

0,90

1995

756960

37521

101098

1192464

635

1,30

1,11

1,36

1,01

1,29

1996

892014

41726

128069

1204238

741

1,18

1,11

1,27

1,01

1,17

1997

985046

45257

153995

1215797

810

1,10

1,08

1,20

1,01

1,09

1998

1045199

45463

175156

1227016

852

1,06

1,00

1,14

1,01

1,05

1999

1098832

40319

186189

1237730

888

1,05

0,89

1,06

1,01

1,04

2000

1192836

40715

193348

1247777

956

1,09

1,01

1,04

1,01

1,08

2001

1316558

46878

203142

1257144

1047

1,10

1,15

1,05

1,01

1,10

2002

1454040

52743

216503

1265938

1149

1,10

1,13

1,07

1,01

1,10

2003

1647918

53505

228371

1274276

1293

1,13

1,01

1,05

1,01

1,13

2004

1936502

60360

245467

1282336

1510

1,18

1,13

1,07

1,01

1,17

2005

2278419

72406

272094

1290336

1766

1,18

1,20

1,11

1,01

1,17

2006

2666772

69468

292559

1298049

2054

1,17

0,96

1,08

1,01

1,16

Средний коэффициент роста

1,10

1,31

1,24

1,01

1,09

Коэффициент роста цепным методом рассчитывается по формуле:

К_pц = 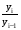. (1)

Средний коэффициент роста цепным методом рассчитывается по формуле:

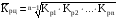. (2)

Как следует из сравнительного анализа динамики данных социально-экономических показателей развития, Великобритания превосходит венгрия по всем показателям роста, кроме темпов роста численности населения. При этом особенно заметно преимущество Великобритании по сравнению с Венгрия в темпах роста привлечения в страну иностранных инвестиций, как flow, так и stock.

Поскольку Великобритания более заметно превосходит Венгрия в темпах роста ВВП, чем Венгрия превосходит Великобритания в темпах роста населения, то как следствие Великобритания имеет более высокие темпы роста среднедушевого ВВП.

Таблица 4 Расчетные корреляции ВВП и инвестиций flow для Венгрия

Годы

х1

х2

х12

х2х1

х2-

(х2-) 2

х22

х2-

(х2-) 2

1970

5862

-14

34363044

-82068

-359

344,9

118956,9

196

-813,6

661936,2

1971

6532

-3

42667024

-19596

-331

328,1

107646,0

9

-802,6

644158,1

1972

7244

60

52475536

434640

-302

361,5

130714,6

3600

-739,6

547000,2

1973

8668

96

75134224

832128

-242

338,4

114545,0

9216

-703,6

495045,4

1974

10929

62

119443041

677598

-149

210,6

44355,6

3844

-737,6

544045,8

1975

13346

81

178115716

1081026

-48

129,3

16717,4

6561

-718,6

516378,2

1976

12730

72

162052900

916560

-74

145,9

21275,5

5184

-727,6

529393,9

1977

11475

42

131675625

481950

-126

167,9

28206,3

1764

-757,6

573949,6

1978

9851

17

97042201

167467

-193

210,3

44246,0

289

-782,6

612454,3

1979

12583

37

158331889

465571

-80

117,0

13680,2

1369

-762,6

581550,5

1980

16740

27

280227600

451980

93

-65,6

4298,6

729

-772,6

596902,4

1981

20448

125

418120704

2556000

246

-121,5

14751,5

15625

-674,6

455077,9

1982

20801

48

432681601

998448

261

-213,1

45414,2

2304

-751,6

564894,4

1983

16142

38

260564164

613396

68

-29,7

884,8

1444

-761,6

580026,3

1984

16923

-89

286387929

-1506147

100

-189,2

35781,1

7921

-888,6

789600,4

1985

14610

1

213452100

14610

4

-3,2

10,0

1

-798,6

637753,3

1986

21725

22

471975625

477950

299

-277,5

76981,0

484

-777,6

604653,4

1987

35586

32

1266363396

1138752

875

-842,7

710180,6

1024

-767,6

589201,5

1988

31082

26

966090724

808132

688

-661,8

437971,9

676

-773,6

598448,6

1989

34947

59

1221292809

2061873

848

-789,2

622839,8

3481

-740,6

548480,4

1990

29281

41

857376961

1200521

613

-572,0

327239,2

1681

-758,6

575465,8

1991

34544

-7

1193287936

-241808

831

-838,5

703042,8

49

-806,6

650594,8

1992

36083

-79

1301982889

-2850557

895

-974,3

949355,9

6241

-878,6

771928,5

1993

34835

761

1213477225

26509435

844

-82,6

6815,1

579121

-38,6

1489,5

1994

44910

3289

2016908100

147708990

1262

2027,3

4109975,9

10817521

2489,4

6197139,3

1995

53635

2557

2876713225

137144695

1624

933,2

870857,2

6538249

1757,4

3088473,8

1996

55813

3471

3115090969

193726923

1714

1756,8

3086362,5

12047841

2671,4

7136406,8

1997

59130

2139

3496356900

126479070

1852

287,1

82449,7

4575321

1339,4

1794006,8

1998

56752

1644

3220789504

93300288

1753

-109,2

11917,3

2702736

844,4

713020,5

1999

51553

1940

2657711809

100012820

1537

402,6

162091,4

3763600

1140,4

1300524,5

2000

53336

810

2844728896

43202160

1611

-801,4

642231,4

656100

10,4

108,3

2001

53954

1144

2911034116

61723376

1637

-493,0

243090,4

1308736

344,4

118615,1

2002

57059

2156

3255729481

123019204

1766

390,1

152172,1

4648336

1356,4

1839835,6

2003

61504

1335

3782742016

82107840

1950

-615,4

378700,8

1782225

535,4

286658,9

2004

69662

1599

4852794244

111389538

2289

-690,0

476051,6

2556801

799,4

639049,0

2005

79382

2579

6301501924

204726178

2692

-113,4

12852,8

6651241

1779,4

3166283,6

2006

90048

3467

8108642304

312196416

3135

332,0

110199,4

12020089

2667,4

7115051,6

Итого

1249705

29585

60875326351

1773925359

29585,00

0,0

14914862,5

70721609,0

0,0

47065602,9

В среднем

33775,8

799,6

1645279090,6

47943928,6

799,6

0,0

403104,4

1911394,8

0,0

1272043,3

Приведем расчет корреляционной зависимости на примере ВВП и инвестиций flow для Венгрия.

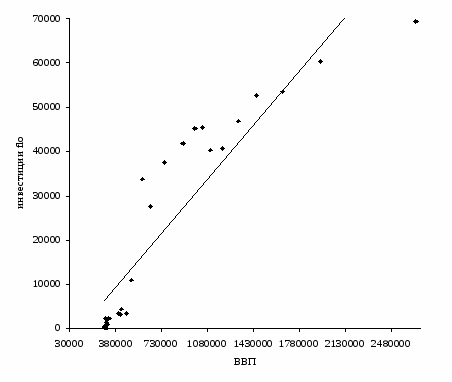
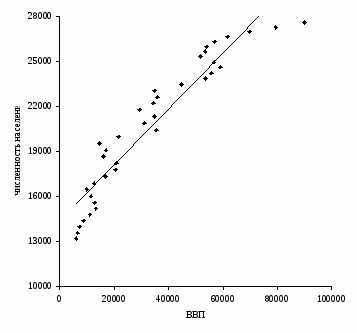
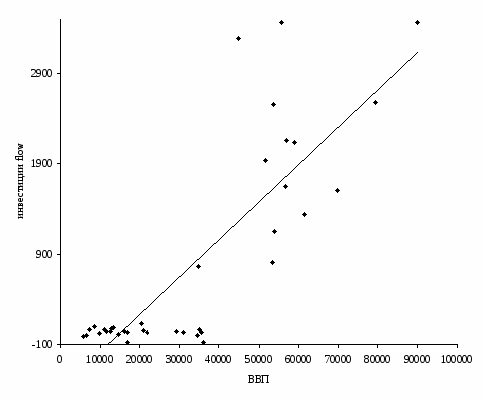
Проведем визуальный анализ данных путем построения корреляционного поля зависимости инвестиций flow от ВВП.

Рисунок 1 Корреляционное поле зависимости инвестиций flow от ВВП

Проанализировав данные и их графическое изображение, можно сделать предположение, что связь между признаками линейная и она описывается уравнением прямой:

х₂ = а₀ + а₁ ∙ х₁. (3)

Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систем нормальных уравнений.

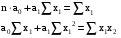(4)

Откуда:

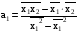(5)

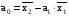(6)

По формулам (5), (6) вычислим а₀, а₁, используя расчетные данные таблицы 4.

.

.

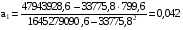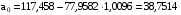Вычислив параметры, получим следующее уравнение регрессии:

х₂ = -602,190 + 0,042 ∙ х₁.

Следовательно, с увеличением ВВП на 1 млн. долл., инвестиции flow увеличатся на 0,42% млн. долл.

Значимость коэффициентов регрессии проверим по t-критерию Стьюдента. Вычислим расчетные значения t-критерия по формулам:

для параметра а₀:

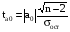, (7)

для параметра а₁:

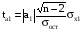, (8)

где n – объем выборки,

среднее квадратическое отклонение результативного признака у от выровненных значений у_х:

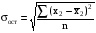, (9)

среднее квадратическое отклонение факторного признака х от общей средней :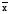

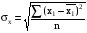. (10)

Находим:

, ,

, .

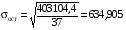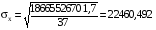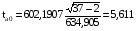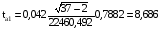Вычисленные значения t_a0 и t_a1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 37–2 =35. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым при условии, если t_расч> t_табл.

Так как t_расча0 = 5,611 больше t_табл = 3,000, параметр а₀ признается значимым, т.е. в этом случае мало вероятно, что найденное значение параметра обусловлено только случайными совпадениями.

Так как t_расча1 = 8,686 больше t_табл = 3,000, следовательно, параметр а₁ также признается значимым.

Выявим тесноту корреляционной связи между х и у с помощью линейного коэффициента корреляции, используя формулу:

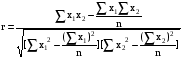. (11)

.

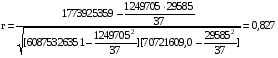Т.к. линейный коэффициент корреляции r = 0,827, то связь между инвестициями flow и ВВП прямая, очень высокая связь.

Значимость линейного коэффициента корреляции определяется помощью t-критерия Стьюдента (число степеней свободы = 35, уровень значимости а = 0,05) по формуле:

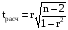. (12)

.

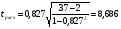Так как 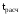= 8,686 больше t_табл = 3,000, следовательно, коэффициент корреляции признается значимым.

Определим линейный коэффициент детерминации r²:

r² = 0,827² = 0,683.

Он показывает, что 68,3% вариации инвестиций flow обусловлено вариацией ВВП.

Теоретическое корреляционное отношение η определим по формуле:

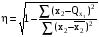. (13)

.

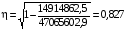Т.к. r = η, то будем считать, что линейная форма связи между х₁ и х₂, выбрана верно.

Аналогично проведем расчет корреляции для остальных параметров.

Уравнение регрессии:

х₃ = 2211,412 + 3,316 ∙ х₂.

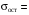3821,256, 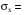1205,708, 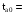3,007, 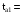5,437.

Вычисленные значения t_a0 и t_a1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 27–2 = 25 при уровне значимости а = 0,05.

Таблица 5 Расчетные корреляции инвестиций flow и stock для Венгрия

Годы

х2

х3

х22

х3х2

х3-

(х3 -) 2

х32

х3 -

(х3 -) 2

1980

27

890

729

24030

2301

-1411,0

1990797,4

792100

-4900,1

24011088,9

1981

125

965

15625

120625

2626

-1661,0

2758816,8

931225

-4825,1

23281697,2

1982

48

1022

2304

49056

2371

-1348,6

1818726,6

1044484

-4768,1

22734883,6

1983

38

1092

1444

41496

2337

-1245,4

1551113,8

1192464

-4698,1

22072248,0

1984

-89

1119

7921

-99591

1916

-797,2

635603,7

1252161

-4671,1

21819279,0

1985

1

1130

1

1130

2215

-1084,7

1176635,7

1276900

-4660,1

21716635,6

1986

22

1152

484

25344

2284

-1132,4

1282270,7

1327104

-4638,1

21512074,7

1987

32

1173

1024

37536

2318

-1144,5

1309968,3

1375929

-4617,1

21317715,0

1988

26

1258

676

32708

2298

-1039,6

1080850,8

1582564

-4532,1

20540031,1

1989

59

1287

3481

75933

2407

-1120,1

1254585,3

1656369

-4503,1

20278009,7

1990

41

1330

1681

54530

2347

-1017,4

1035075,4

1768900

-4460,1

19892591,1

1991

-7

1370

49

-9590

2188

-818,2

669445,9

1876900

-4420,1

19537382,2

1992

-79

1504

6241

-118816

1949

-445,4

198391,9

2262016

-4286,1

18370748,5

1993

761

1642

579121

1249562

4735

-3093,2

9568091,5

2696164

-4148,1

17206825,8

1994

3289

4451

10817521

14639339

13119

-8668,2

75138177,8

19811401

-1339,1

1793218,6

1995

2557

5510

6538249

14089070

10692

-5181,6

26848812,5

30360100

-280,1

78462,2

1996

3471

6720

12047841

23325120

13723

-7002,8

49039524,8

45158400

929,9

864693,3

1997

2139

7753

4575321

16583667

9305

-1552,3

2409655,0

60109009

1962,9

3852932,8

1998

1644

8297

2702736

13640268

7664

633,3

401117,3

68840209

2506,9

6284491,9

1999

1940

9791

3763600

18994540

8645

1145,7

1312555,0

95863681

4000,9

16007111,9

2000

810

11062

656100

8960220

4898

6164,3

37998108,6

122367844

5271,9

27792812,5

2001

1144

11835

1308736

13539240

6005

5829,6

33983828,8

140067225

6044,9

36540681,7

2002

2156

12549

4648336

27055644

9362

3187,3

10158970,2

157477401

6758,9

45682579,0

2003

1335

12876

1782225

17189460

6639

6237,1

38901696,0

165791376

7085,9

50209821,3

2004

1599

13310

2556801

21282690

7514

5795,6

33588731,8

177156100

7519,9

56548728,9

2005

2579

15889

6651241

40977731

10765

5124,5

26260029,2

252460321

10098,9

101987556,8

2006

3467

19356

12020089

67107252

13710

5646,4

31882320,6

374654736

13565,9

184033341,3

Итого

29135

156333

70689577

298868194

156333,00

0,0

394253901,3

1731153083,0

0,0

825967642,7

В среднем

1079,1

5790,1

2618132,5

11069192,4

5790,1

0,0

14601996,3

64116780,9

0,0

30591394,2

Так как t_а0 = 3,007 меньше t_табл = 3,080, параметр а₀ признается незначимым.

Так как t_а1 = 5,437 больше t_табл = 3,080, следовательно, параметр а₁ признается значимым.

Линейный коэффициент корреляции:

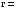0,723.

Т.к. r = 0,723, то связь между инвестициями stock и flow, прямая, высокая связь.

Так как 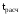= 5,232 больше t_табл = 3,080, следовательно, коэффициент корреляции признается значимым.

Определим линейный коэффициент детерминации r²:

r² = 0,723² = 0,523.

Он показывает, что 52,3% вариации инвестиций stock обусловлено вариацией инвестиций flow.

Т.к. r = η, то будем считать, что линейная форма связи между х₂ и х₃, выбрана верно.

2.2 Анализ корреляционных связей и темпов экономического роста

Таблица 6 Расчетные корреляции ВВП и численности населения для Венгрия

Годы

х1

х4

х12

х4х1

х4 -

(х4 -) 2

х42

х4 -

(х4 -) 2

1970

5862

13193

34363044

77337366

15492

-2299,0

5285369,4

174055249

-7497,7

56215140,5

1971

6532

13567

42667024

88619644

15617

-2049,8

4201574,6

184063489

-7123,7

50746755,1

1972

7244

13951

52475536

101061044

15749

-1798,4

3234161,7

194630401

-6739,7

45423228,2

1973

8668

14345

75134224

124342460

16015

-1669,6

2787510,8

205779025

-6345,7

40267599,8

1974

10929

14749

119443041

161191821

16436

-1686,7

2844868,6

217533001

-5941,7

35303509,8

1975

13346

15161

178115716

202338706

16886

-1724,8

2974994,2

229855921

-5529,7

30577313,1

1976

12730

15582

162052900

198358860

16771

-1189,1

1413942,2

242798724

-5108,7

26098567,2

1977

11475

16012

131675625

183737700

16537

-525,4

276004,3

256384144

-4678,7

21890006,1

1978

9851

16447

97042201

162019397

16235

212,1

44983,6

270503809

-4243,7

18008783,2

1979

12583

16886

158331889

212476538

16744

142,3

20244,8

285136996

-3804,7

14475557,0

1980

16740

17325

280227600

290020500

17518

-192,9

37217,1

300155625

-3365,7

11327772,8

1981

20448

17763

418120704

363217824

18208

-445,5

198467,8

315524169

-2927,7

8571284,9

1982

20801

18200

432681601

378578200

18274

-74,2

5511,6

331240000

-2490,7

6203465,3

1983

16142

18638

260564164

300854596

17407

1231,5

1516479,8

347375044

-2052,7

4213477,4

1984

16923

19079

286387929

322873917

17552

1527,0

2331730,6

364008241

-1611,7

2597498,5

1985

14610

19523

213452100

285231030

17121

2401,8

5768522,3

381147529

-1167,7

1363466,5

1986

21725

19972

471975625

433891700

18446

1525,7

2327679,8

398880784

-718,7

516494,7

1987

35586

20422

1266363396

726737292

21028

-605,8

367001,2

417058084

-268,7

72186,6

1988

31082

20872

966090724

648743504

20189

683,0

466517,7

435640384

181,3

32878,5

1989

34947

21320

1221292809

745070040

20909

411,2

169086,6

454542400

629,3

396049,1

1990

29281

21762

857376961

637213122

19854

1908,4

3642144,0

473584644

1071,3

1147735,8

1991

34544

22199

1193287936

766842256

20834

1365,3

1863925,0

492795601

1508,3

2275042,3

1992

36083

22628

1301982889

816486124

21120

1507,6

2272954,9

512026384

1937,3

3753225,5

1993

34835

23050

1213477225

802946750

20888

2162,1

4674505,1

531302500

2359,3

5566411,3

1994

44910

23460

2016908100

1053588600

22764

695,7

483980,6

550371600

2769,3

7669157,2

1995

53635

23857

2876713225

1279570195

24389

-532,3

283302,1

569156449

3166,3

10025609,7

1996

55813

24242

3115090969

1353018746

24795

-552,9

305690,9

587674564

3551,3

12611904,5

1997

59130

24613

3496356900

1455366690

25413

-799,7

639444,9

605799769

3922,3

15384628,1

1998

56752

24973

3220789504

1417267696

24970

3,2

10,4

623650729

4282,3

18338301,6

1999

51553

25322

2657711809

1305425066

24002

1320,5

1743697,6

641203684

4631,3

21449165,0

2000

53336

25663

2844728896

1368761768

24334

1329,4

1767369,7

658589569

4972,3

24724009,2

2001

53954

25995

2911034116

1402534230

24449

1546,3

2391130,1

675740025

5304,3

28135856,5

2002

57059

26321

3255729481

1501849939

25027

1294,1

1674568,4

692795041

5630,3

31700552,0

2003

61504

26641

3782742016

1638528064

25855

786,2

618129,4

709742881

5950,3

35406359,6

2004

69662

26959

4852794244

1878017858

27374

-415,1

172339,6

726787681

6268,3

39291889,8

2005

79382

27274

6301501924

2165064668

29184

-1910,4

3649612,6

743871076

6583,3

43340159,2

2006

90048

27589

8108642304

2484334272

31171

-3581,8

12829558,2

761152921

6898,3

47586878,5

Итого

1249705

765555

60875326351

29333518183

765555,00

0,0

75284232,5

16562558137,0

0,0

722707920,1

В среднем

33775,8

20690,7

1645279090,6

792797788,7

20690,7

0,0

2034709,0

447636706,4

0,0

19532646,5

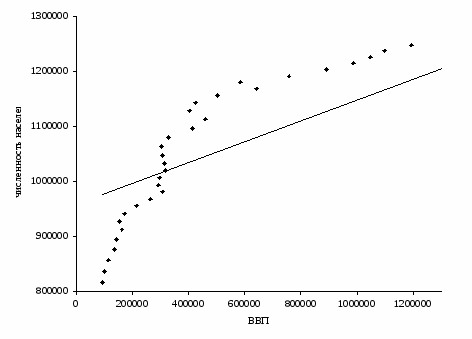
Рисунок 3 Корреляционное поле зависимости численности населения от ВВП

Вычислив параметры, получим следующее уравнение регрессии:

х₄ = 14400,251 + 0,186 ∙ х₁.

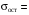1426,432, 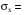22460,492, 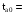59,725, 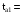17,349.

Вычисленные значения t_a0 и t_a1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 37–2 = 35 при уровне значимости а = 0,05.

Так как t_а0 = 59,725 меньше t_табл = 3,000, параметр а₀ признается значимым.

Так как t_а1 = 17,349 больше t_табл = 3,000, следовательно, параметр а₁ признается значимым.

Линейный коэффициент корреляции:

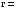0,946.

Т.к. r = 0,946, то связь между ВВП и численностью населения Венгрия прямая, полная связь.

Так как 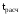= 17,349 больше t_табл = 3,000, следовательно, коэффициент корреляции признается значимым.

Линейный коэффициент детерминации r²:

r² = 0,946² = 0,896.

Он показывает, что 89,6% вариации численности населения Венгрия обусловлено вариацией ВВП.

Т.к. r = η, то будем считать, что линейная форма связи между х₁ и х₄, выбрана верно.

Таблица 7 Расчетные корреляции ВВП и инвестиций flow для Великобритании

Годы

у1

у2

у12

у2у1

у2-

(у2-) 2

у22

у2-

(у2-) 2

1980

306520

57

93954510400

17471640

6811

-6753,6

45610866,6

3249

-25968,6

674369724,8

1981

293852

265

86348997904

77870780

6369

-6104,2

37261741,6

70225

-25760,6

663610038,9

1982

295370

430

87243436900

127009100

6422

-5992,1

35905567,4

184900

-25595,6

655136256,1

1983

317352

916

100712291904

290694432

7188

-6272,0

39337472,5

839056

-25109,6

630493500,1

1984

314637

1419

98996441769

446469903

7093

-5674,4

32198486,1

2013561

-24606,6

605486221,7

1985

309083

1956

95532300889

604566348

6900

-4943,9

24441894,6

3825936

-24069,6

579347070,5

1986

304348

2244

92627705104

682956912

6735

-4490,9

20168283,1

5035536

-23781,6

565565907,8

1987

329851

2314

108801682201

763275214

7623

-5309,4

28189872,0

5354596

-23711,6

562241379,7

1988

413439

3194

170931806721

1320524166

10536

-7341,5

53898309,5

10201636

-22831,6

521283311,5

1989

459782

3393

211399487524

1560040326

12150

-8757,1

76686741,8

11512449

-22632,6

512235924,0

1990

404494

3487

163615396036

1410470578

10224

-6736,9

45385966,9

12159169

-22538,6

507989825,6

1991

424117

4366

179875229689

1851694822

10908

-6541,6

42791994,8

19061956

-21659,6

469139555,7

1992

499859

11008

249859019881

5502447872

13546

-2538,3

6443192,9

121176064

-15017,6

225529199,7

1993

641069

27515

410969462761

17639013535

18466

9049,0

81884795,5

757075225

1489,4

2218224,1

1994

582653

33767

339484518409

19674443851

16431

17336,2

300543292,2

1140210289

7741,4

59928815,2

1995

756960

37521

572988441600

28401896160

22504

15017,5

225524707,5

1407825441

11495,4

132143540,0

1996

892014

41726

795688976196

37220176164

27209

14517,3

210752465,7

1741059076

15700,4

246501629,8

1997

985046

45257

970315622116

44580226822

30450

14807,2

219252047,2

2048196049

19231,4

369845606,3

1998

1045199

45463

1092440949601

47517882137

32546

12917,5

166861387,1

2066884369

19437,4

377811366,9

1999

1098832

40319

1207431764224

44303807408

34414

5905,0

34868513,2

1625621761

14293,4

204300436,5

2000

1192836

40715

1422857722896

48566317740

37689

3025,9

9156306,8

1657711225

14689,4

215777601,9

2001

1316558

46878

1733324967364

61717605924

41999

4878,6

23800465,0

2197546884

20852,4

434821350,1

2002

1454040

52743

2114232321600

76690431720

46789

5953,8

35447956,0

2781824049

26717,4

713817879,5

2003

1647918

53505

2715633734724

88171852590

53544

-38,7

1499,4

2862785025

27479,4

755115796,0

2004

1936502

60360

3750039996004

116887260720

63598

-3237,7

10482948,8

3643329600

34334,4

1178848988,7

2005

2278419

72406

5191193139561

164971206114

75510

-3103,8

9633756,9

5242628836

46380,4

2151138755,7

2006

2666772

69468

7111672899984

185255317296

89040

-19571,7

383051849,5

4825803024

43442,4

1887239543,4

Итого

23167522

702692

31168172823962

996252930274

702692,00

0,0

2199582380,2

34189939186,0

0,0

15901937450,3

В среднем

858056,4

26025,6

1154376771257,9

36898256676,8

26025,6

0,0

81466014,1

1266294043,9

0,0

588960646,3

Рисунок 4 Корреляционное поле зависимости инвестиций flow от ВВП

Уравнение регрессии:

у₂ = -3868,309 + 0,035 ∙ у₁.

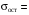9025,853, 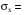646618,927, 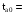2,143, 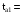12,480.

Так как t_расча0 = 2,143 меньше t_табл = 3,000, параметр а₀ признается незначимым, т.е. в этом случае вероятно, что найденное значение параметра обусловлено только случайными совпадениями.

Так как t_расча1 = 12,480 больше t_табл = 3,000, следовательно, параметр а₁ также признается значимым.

Линейный коэффициент корреляции:

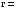0,928.

Т.к. линейный коэффициент корреляции r = 0,928, то связь между инвестициями flow и ВВП прямая, полная связь.

Так как 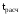= 12,480 больше t_табл = 3,000, следовательно, коэффициент корреляции признается значимым.

Линейный коэффициент детерминации r²:

r² = 0,928² = 0,862.

Он показывает, что 86,2% вариации инвестиций flow обусловлено вариацией ВВП.

Т.к. r = η, то будем считать, что линейная форма связи между у₁ и у₂, выбрана верно.

Уравнение регрессии:

у₃ = -3159,825 + 3,939 ∙ у₂.

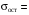21642,509, 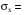24268,511, 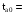0,759, 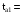22,950.

Так как t_а0 = 0,759 меньше t_табл = 3,080, параметр а₀ признается незначимым.

Таблица 8 Расчетные корреляции инвестиций flow и stock для Великобритании

Годы

у2

у3

у22

у3у2

у3-

(у3 -) 2

у32

у3 -

(у3 -) 2

1980

57

1074

3249

61218

-2935

4009,3

16074563,3

1153476

-98277,9

9658536164,6

1981

265

1339

70225

354835

-2116

3455,0

11937189,3

1792921

-98012,9

9606519128,1

1982

430

1769

184900

760670

-1466

3235,1

10465933,9

3129361

-97582,9

9522412975,5

1983

916

2685

839056

2459460

448

2236,8

5003349,3

7209225

-96666,9

9344480246,9

1984

1419

4104

2013561

5823576

2429

1674,6

2804161,7

16842816

-95247,9

9072153282,4

1985

1956

6060

3825936

11853360

4545

1515,4

2296400,1

36723600

-93291,9

8703369621,9

1986

2244

8304

5035536

18634176

5679

2625,0

6890583,2

68956416

-91047,9

8289711326,8

1987

2314

10617

5354596

24567738

5955

4662,3

21736769,4

112720689

-88734,9

7873873933,2

1988

3194

13811

10201636

44112334

9421

4390,1

19272641,6

190743721

-85540,9

7317237335,5

1989

3393

17204

11512449

58373172

10205

6999,2

48989161,0

295977616

-82147,9

6748269563,9

1990

3487

20691

12159169

72149517

10575

10116,0

102332881,1

428117481

-78660,9

6187529614,1

1991

4366

25057

19061956

109398862

14037

11019,7

121433816,5

627853249

-74294,9

5519725011,7

1992

11008

36064

121176064

396992512

40199

-4135,3

17100707,5

1300612096

-63287,9

4005352192,0

1993

27515

63579

757075225

1749376185

105218

-41639,3

1733830818,0

4042289241

-35772,9

1279696929,6

1994

33767

74151

1140210289

2503856817

129844

-55693,1

3101725256,8

5498370801

-25200,9

635082934,1

1995

37521

101098

1407825441

3793298058

144631

-43532,7

1895093177,2

10220805604

1746,1

3049033,4

1996

41726

128069

1741059076

5343807094

161194

-33124,6

1097241332,8

16401668761

28717,1

824674597,8

1997

45257

153995

2048196049

6969351715

175102

-21106,8

445496905,1

23714460025

54643,1

2985873639,5

1998

45463

175156

2066884369

7963117228

175913

-757,2

573360,4

30679624336

75804,1

5746268876,5

1999

40319

186189

1625621761

7506954291

155652

30537,4

932530506,6

34666343721

86837,1

7540690298,5

2000

40715

193348

1657711225

7872163820

157211

36136,6

1305851571,7

37383449104

93996,1

8835275866,7

2001

46878

203142

2197546884

9522890676

181487

21655,3

468951479,2

41266672164

103790,1

10772394852,6

2002

52743

216503

2781824049

11419017729

204588

11914,8

141962250,2

46873549009

117151,1

13724391512,4

2003

53505

228371

2862785025

12218990355

207590

20781,4

431865306,2

52153313641

129019,1

16645940588,9

2004

60360

245467

3643329600

14816388120

234591

10876,4

118295806,7

60254048089

146115,1

21349636518,4

2005

72406

272094

5242628836

19701238164

282038

-9944,3

98888889,0

74035144836

172742,1

29839849746,8

2006

69468

292559

4825803024

20323488612

270466

22093,1

488106070,8

85590768481

193207,1

37329002095,5

Итого

702692

2682500

34189939186

132449480294

2682500,00

0,0

12646750888,4

525872340480,0

0,0

259360997887,4

В среднем

26025,6

99351,9

1266294043,9

4905536307,2

99351,9

0,0

468398181,1

19476753351,1

0,0

9605962884,7

Так как t_а1 = 22,950 больше t_табл = 3,080, следовательно, параметр а₁ признается значимым.

Линейный коэффициент корреляции:

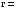0,975.

Т.к. r = 0,975, то связь между инвестициями stock и flow, прямая, полная.

Так как 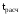= 22,084 больше t_табл = 3,080, следовательно, коэффициент корреляции признается значимым.

Определим линейный коэффициент детерминации r²:

r² = 0,975² = 0,951.

Он показывает, что 95,1% вариации инвестиций stock обусловлено вариацией инвестиций flow.

Т.к. r = η, то будем считать, что линейная форма связи между х₂ и х₃, выбрана верно.

Рисунок 6 Корреляционное поле зависимости численности населения от ВВП

Вычислив параметры, получим следующее уравнение регрессии:

у₄ = 960230,354 + 0,189 ∙ у₁.

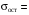80354,857, 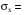635176,603, 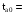70,696, 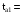8,825.

Так как t_а0 = 70,696 больше t_табл = 3,000, параметр а₀ признается значимым.

Так как t_а1 = 8,825 больше t_табл = 3,000, следовательно, параметр а₁ признается значимым.

Линейный коэффициент корреляции:

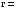0,831.

Т.к. r = 0,831, то связь между ВВП и численностью населения Великобритании прямая, полная связь.

Так как 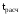= 8,825 больше t_табл = 3,000, следовательно, коэффициент корреляции признается значимым.

Линейный коэффициент детерминации r²:

r² = 0,831² = 0,690.

Он показывает, что 69,0% вариации численности населения Великобритании обусловлено вариацией ВВП.

Т.к. r = η, то будем считать, что линейная форма связи между х₁ и х₄, выбрана верно.

Заключение

Таким образом, значимыми приняты все рассмотренные связи:

1) между инвестициями flow и ВВП Венгрия (прямая, очень высокая связь);

2) между инвестициями stock и flow (прямая, высокая связь);

3) между ВВП и численностью населения Венгрия (прямая, полная связь);

4) между инвестициями flow и ВВП Великобритании (прямая, полная связь);

5) между инвестициями stock и flow Великобритании (прямая, полная связь);

6) между ВВП и численностью населения Великобритании (прямая, полная связь).

Незначимым признан параметр а₀ для связей:

1) между инвестициями stock и flow Венгрия;

2) между инвестициями flow и ВВП Великобритании;

3) между инвестициями stock и flow Великобритании.

В целом все исследованные модели являются адекватными и на их основе можно делать прогнозы.

Список литературы

1. В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский «Теория вероятностей и математическая сатистика»/ М., 1991.

2. «Теория Статистики» под редакцией Р.А. Шмойловой/ «ФиС», 1998.

3. «Многомерный статистический анализ на ЭBM с использованием пакета Microsoft Excel»/ М., 1997.

4. А.А. Френкель, Е.В. Адамова «Корреляционно регрессионный анализ в экономических приложениях»/ М., 1987.

5. И.Д. Одинцов «Теория статистики»/ М., 1998.

6. А.Н. Кленин, К.К. Шевченко «Математическая статистика для экономистов-статистиков»/ М., 1990.