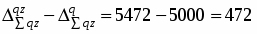
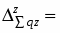
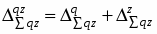
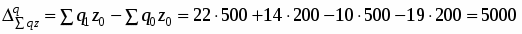
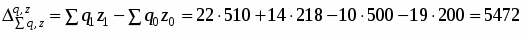
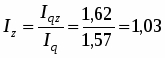
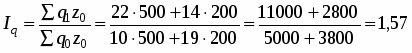
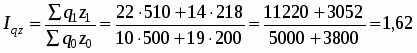
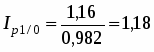
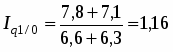
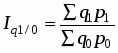
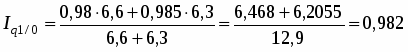
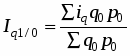
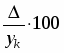
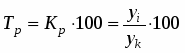
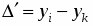
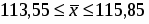
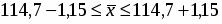
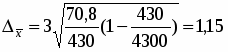
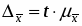
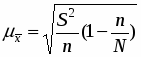
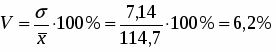
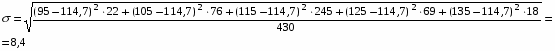
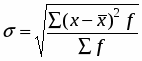
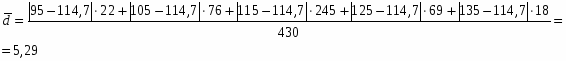
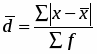
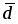
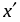
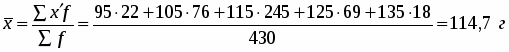Содержание

Задача №5

Задача №12

Задача №21

Задача №23

Список использованной литературы

Задача №5

В целях контроля за соблюдением норма расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 10% изделий получены следующие данные о весе обследованных единиц:

Вес изделия, г

Число образцов, шт.

До 100

22

100 – 110

76

110 – 120

245

120 – 130

69

130 и выше

18

Итого

430

На основании данных выборочного обследования вычислите:

1. Средний вес изделия.

2. Среднее линейное отклонение.

3. Дисперсию.

4. Среднее квадратическое отклонение.

5. Коэффициент вариации.

6. С вероятностью 0,997 возможные границы, в которых заключен средний вес изделия во всей партии.

Решение:

Введем условные обозначения:

х – вес изделия, г;

f – число образцов в каждой группе.

Средняя арифметическая для интервального ряда распределения:

- середина соответствующего интервала значения признака; вычисляется как средняя из значений границ интервала.

Среднее линейное отклонение () и среднее квадратическое отклонение () показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения

Среднее линейное отклонение определяется по формуле:

.

Среднее квадратическое отклонение () и дисперсия (²) определяются по формулам:

² = (8,4)² = 70,8

Коэффициент вариации вычисляется по формуле:

Так как коэффициент вариации меньше 33% можно говорить о том, что совокупность однородна.

Механическая выборка заключается в отборе единиц из генеральной совокупности через равные промежутки из определенного расположения их в генеральной совокупности.

Если в генеральной совокупности единицы располагаются случайным образом по отношению к изучаемому признаку, то механический отбор можно рассматривать как разновидность случайного бесповторного отбора; поэтому для оценки ошибки механической выборки применяются формулы случайной бесповторной выборки.

,

,

Где N – общая численность единиц в генеральной совокупности; N = 430  100 / 10 = 4 300 ед.;

n – объем выборочной совокупности; n = 430 ед.

t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки. В зависимости от принятой вероятности Р определяется значение коэффициента кратности (t) по удвоенной нормированной функции Лапласа.

При вероятности Р = 0,997 t = 3,0.

Задача №12

Имеются следующие данные по региону:

Годы

Добыча железной руды, тыс. т

Базисные показатели динамики

Абсолютные приросты, тыс. т

Темы роста, %

Темпы прироста, %

1992

308

-

100,0

-

1993

15,1

1994

105,3

1995

6,6

1996

110,1

1997

8,9

Определите недостающие показатели.

Решение:

При расчете базисных показателей динамики приняты следующие условные обозначения:

y_i – уровень любого периода (кроме первого), называемый уровнем текущего периода;

y_к– уровень, принятый за постоянную базу сравнения (начальный уровень).

Абсолютный прирост показывает на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного. Данный показатель вычисляется по формуле:

Темп роста – это коэффициент роста, выраженный в процентах; он показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периода. Данный показатель вычисляется по формуле:

.

Темп прироста показывает, на сколько процентов уровень текущего периода больше (или меньше) уровня базисного периода. Данный показатель вычисляется по формуле:

Т_п = (К_р – 1)  100 = Т_р – 100 = .

Расчет показателей приведен в таблице.

Годы

Добыча железной руды, тыс. т

Базисные показатели динамики

Абсолютные приросты, тыс. т

Темы роста, %

Темпы прироста, %

1992

308

-

100,0

-

1993

308 + 15,1 = 323,1

15,1

323,1*100/308=104,9

104,9-100=4,9

1994

105,3*308/100=324,3

324,3 – 308 = 16,3

105,3

105,3-100=5,3

1995

308*106,6/100=328,3

328,3 – 308 = 20,3

100 + 6,6 = 106,6

6,6

1996

308*110,1/100=339,1

339,1 – 308 = 31,1

110,1

110,1-100=10,1

1997

308 + 8,9 = 316,9

8,9

316,9*100/308 = 102,9

102,9-100=2,9

Задача №21

Имеются следующие данные о реализации товаров:

Наименование товара

Товарооборот в фактических ценах, тыс. руб.

Изменение количества реализованных товаров в отчетном периоде по сравнению с базисным, %

(i_q)

Базисный период (q₀p₀)

Отчетный период (q₁p₁)

Портфели

6,6

7,8

-2

Сумки

6,3

7,1

-1,5

Определите:

1. Общий индекс физического объема товарооборота.

2. Общий индекс товарооборота.

3. Общий индекс цен.

Решение:

Индекс – относительная величина, характеризирующая изменение уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом.

По степени охвата элементов совокупности различают индивидуальные и общие индексы.

Средний взвешенный индекс физического объема товарооборота вычисляется по формуле:

, где

i_q – индивидуальный индекс по каждому виду продукции;

q₀p₀ – товарооборот продукции каждого вида в базисном периоде.

Агрегатный индекс товарооборота I_{q 1/0} характеризует изменение товарооборота всей совокупности продукции и исчисляется по формуле:

, где

q₁, q₀ – количество единиц отдельных видов реализованной продукции соответственно в отчетном и базисном периодах;

p₀, р₁– цена единицы отдельного вида продукции в базисном периоде и отчетном периодах соответственно.

Общий индекс цен вычисляется как:

.

Задача №23

Имеются следующие данные:

Вид продукции

Произведено продукции, тыс. шт.

Себестоимость 1 шт., руб.

базисный q₀

отчетный q₁

базисный z₀

отчетный z₁

Столы

19

22

500

510

Стулья

10

14

200

218

Определите:

1) общие индексы себестоимость единицы продукции, физического объема продукции, затрат на производство продукции;

2) абсолютное изменение затрат на производство – общее и за счет изменения себестоимость единицы продукции и физического объема продукции.

Решение:

1) Общий индекс затрат на производство продукции:

Общий индекс физического объема продукции:

Общий индекс себестоимости:

2) Абсолютное изменение общей суммы затрат на производство продукции за счет изменения количества продукции и ее себестоимости

тыс. руб.

Абсолютное изменение общей стоимости продукции за счет изменения физического объема:

тыс. руб.

Так как общее абсолютное изменение затрат вычисляется по формуле:

, то

тыс. руб.

Общая сумма затрат на производство продукции увеличилась на 5472 тыс. руб., в том числе за счет изменения себестоимости единицы продукции – на 472 тыс. руб.; за счет изменения физического объема продукции – на 5000 тыс. руб.

Список использованной литературы

1. Елисеева И. И., Юзбашев М. М. Общая теория статистики. – М.: Финансы и статистика, 2004.

2. Ефимова М. Р., Ганченко О. И., Петрова Е. В. Практикум по общей теории статистики. – М.: Финансы и статистика, 2004.

3. Ефимова М. Р. и до. Общая теория статистики. – М.: ИНФРА-М, 2004.

4. Общая теория статистики / Под ред. О. Э. Башиной, А. А. Спирина. – М.: Финансы и статистика, 2003.

5. Статистика / Под ред. М. Р. Ефимовой. – М.: ИНФРА-М, 2000.