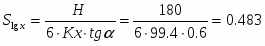
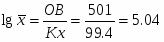
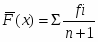
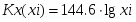
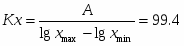
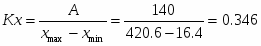
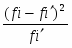
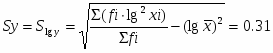
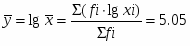
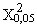
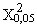
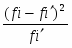
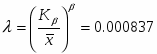
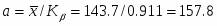
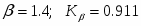
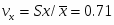
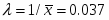
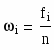
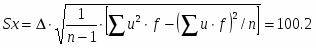
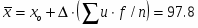
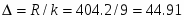
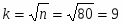
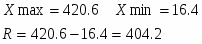
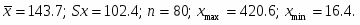
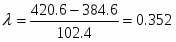
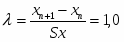
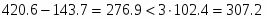
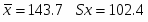
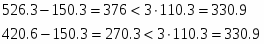
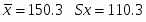
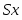
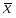
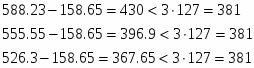
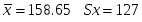
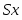
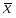
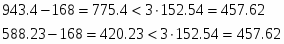
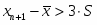
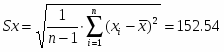
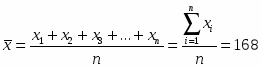
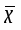ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Институт транспортной техники и организации производства

(ИТТОП)

Кафедра: «Локомотивы и локомотивное хозяйство»

Курсовой проект

на тему:

«Статистические методы обработки выборочных данных наблюдений или экспериментов»

Выполнил: студент Краснов М.А.

группы ТЛТ-451

Принял: Пузанков А.Д.

Москва 2009

СОДЕРЖАНИЕ

1. ПЕРВИЧНЫЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

2. ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ АНАЛИЗИРУЕМОЙ ВЕЛИЧИНЫ И РАСЧЕТ ЕЕ ХАРАКТЕРИСТИК

3. ОПРЕДЕЛЕНИЕ ВИДА ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И РАСЧЕТ ЕГО ПАРАМЕТРОВ ПРИ ПОМОЩИ МЕТОДА МОМЕНТОВ

4. ОПРЕДЕЛЕНИЕ ВИДА ТЕОРЕТИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ГРАФИЧЕСКИМ МЕТОДОМ

1. Первичный анализ экспериментальных данных

Запишем полученные значения в вариационный ряд в возрастающем порядке:

Таблица 1.

16,4

21,6

35,46

38,76

39,84

40,65

44,25

46,73

47,62

50,25

50,25

51,02

51,8

55,22

55,25

55,55

61,73

63,3

64,93

67,56

68,5

68,5

71,94

73

73,53

73,53

74,07

77,52

78,12

78,74

78,74

80,64

85,47

86,2

87,72

90,1

92,6

94,34

95,24

96,15

99,01

99,01

106,4

108,6

116,28

133,3

135,13

137

144,93

149,25

153,84

161,3

166,7

172,4

172,4

175,44

178,6

178,6

185,18

192,3

208,33

212,76

227,27

232,56

238,1

243,9

256,41

277,8

277,8

285,7

285,71

285,71

322,6

322,6

344,83

370,4

370,4

370,4

384,6

420,6

526,3

555,55

588,23

943,4

x_max = 943,4; x_min = 16,4

Результат последних двух измерений вызывает сомнения. Поэтому выполняем проверку:

Величину выборочного среднего находим из соотношения:

(1)

Корень квадратный из дисперсии, взятый с положительным знаком, называется среднеквадратическим отклонением и рассчитывается по формуле:

(2)

Упрощённая проверка сомнительного результата на брак выполняется из условия:

Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последнее одно значение, отбрасываем их и пересчитываем и :

Проверяем по упрощённой проверки:

Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последние два значения, отбрасываем их и пересчитываем и :

Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последнее одно значение, отбрасываем их и пересчитываем и :

Таким образом, по упрощенной проверке результат сомнительного измерения не является браком.

Так же выполним подобную проверку с помощью критерия Ирвина:

Таким образом, по расчётам обеих проверок результат последнего сомнительного измерения не является браком.

Из этого следует, что нужно произвести повторный расчёт, но уже без данного измерения:

2. Построение эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик

Определяем размах имеющихся данных, т.е. разности между наибольшим и наименьшим выборочным значениями (R = Xmax – Xmin):

Выбор числа интервалов группировки k при числе наблюдений n<100 – ориентировочное значение интервалов можно рассчитать с использованием формулы Хайнхольда и Гаеде:

Тогда ширина интервала:

Результат подсчёта частот и характеристик эмпирического распределения

Таблица 2.

Границы интервала

группировки

Ср.знач.

интерв.

Распределение

данных

f_i

U

U*f

U^2*f

16,4…61,31

38,86

////////////////

16

-1

-16

16

61,31…106,22

83,77

//////////////////////////

26

0

0

0

106,22…151,13

128,68

////////

8

1

8

8

151,13…196,04

173,59

//////////

10

2

20

40

196,04…240,96

218,50

/////

5

3

15

45

240,96…285,87

263,41

/////

5

4

20

80

285,87…330,78

308,32

////

4

5

20

100

330,78…375,69

353,23

////

4

6

24

144

375,69…420,60

398,14

//

2

7

14

98

ИТОГО

80

 

105

531

Принимаем «ложный нуль» x₀=83,77 и обозначаем нулем тот интервал, которому соответствует максимальная частота (f=26). Далее, для интервалов, следующих к наименьшему наблюдаемому значению вписываем -1, -2 … и 1, 2, … для интервалов, следующих к наибольшему значению наблюдаемой величины.

Выборочное среднее х и среднеквадратическое отклонение Sx рассчитываем, используя следующие выражения:

(3)

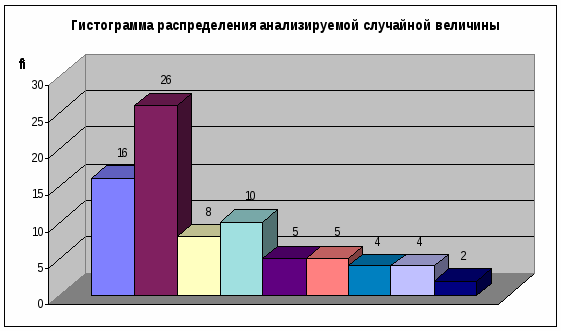
Для построения гистограммы, приведённой на рис.1, по оси абсцисс в выбранном масштабе отмечаем границы интервалов. Левая ось размечается масштабом частот, а на правую, в случае необходимости, можно нанести шкалу относительных частот. На чистом поле гистограммы указываются значения: числа данных; среднего арифметического; среднеквадратического отклонения.

Рис.1

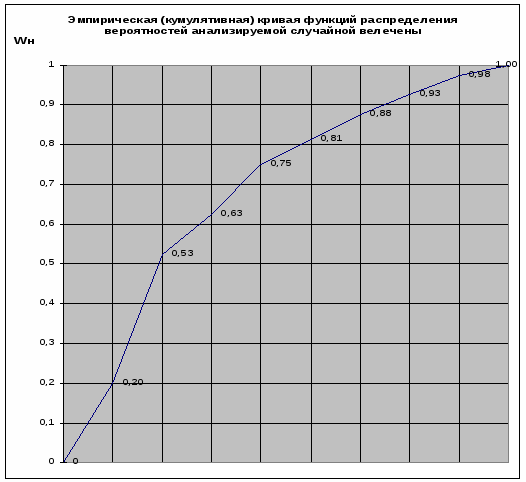
Помимо гистограммы эмпирические данные измерений случайной величины могут быть представлены в виде кумулятивной кривой функции распределения вероятностей. Для этого данные, представленные в табл.1., должны быть дополнены частостями (см. табл.2.).

Частость находим из соотношения:

Таблица частот f и частостей ω.

Таблица 3.

Границы интервала

группировки

Частота,fi

Частость,

ω i

Накопленная

частость, ω н

16,4…61,31

16

0,20

0,20

61,31…106,22

26

0,33

0,53

106,22…151,13

8

0,10

0,63

151,13…196,04

10

0,13

0,75

196,04…240,96

5

0,06

0,81

240,96…285,87

5

0,06

0,88

285,87…330,78

4

0,05

0,93

330,78…375,69

4

0,05

0,98

375,69…420,60

2

0,03

1,00

ИТОГО

80

1

Рис. 2

3. Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов

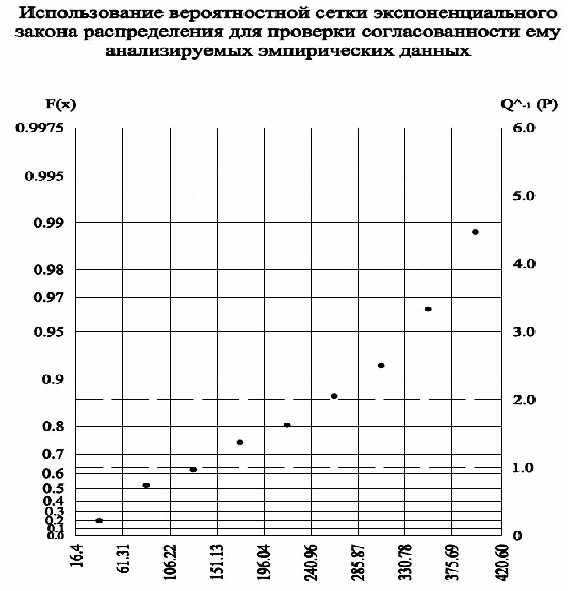
Экспоненциальный (нормальный) закон распределения

Параметр закона распределения:

Таблица 4

№

xi

10³ км

fi

шт

λ*xi

e^-λ*xi

φ(xi)

10^-6

fi’

шт

1

38,86

16

0,270

0,763

0,531

19,08

0,50

2

83,77

26

0,583

0,558

0,388

13,96

10,39

3

128,68

8

0,895

0,408

0,284

10,21

0,48

4

173,59

10

1,208

0,299

0,208

7,47

0,86

5

218,50

5

1,520

0,219

0,152

5,47

0,04

6

263,41

5

1,833

0,160

0,111

4,00

0,25

7

308,32

4

2,145

0,117

0,081

2,93

0,39

8

353,23

4

2,458

0,086

0,060

2,14

1,62

9

398,14

2

2,770

0,063

0,044

1,57

0,12

ИТОГО:

80

14,64

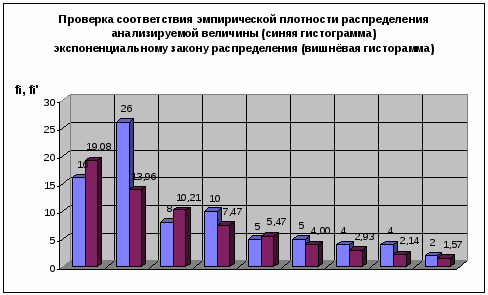
Рис. 4

Нормальный закон распределения двухпараметрический, число степеней свободы υ = 7 и = 14,067.

Так как χ² > χ_0,05², то гипотеза о принадлежности эмпирической выборки значений, экспоненциальному закону распределения отвергается

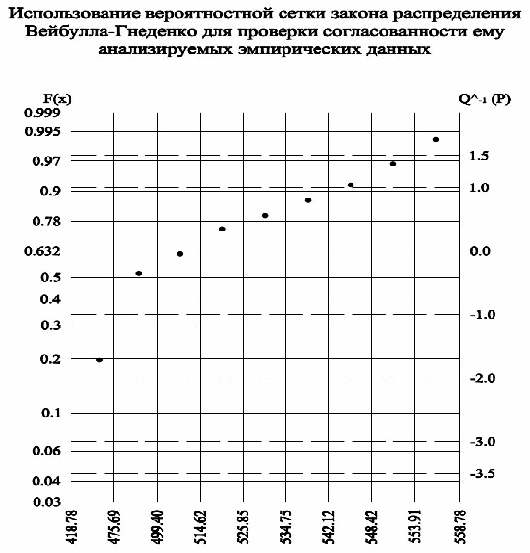
Распределение Вейбулла - Гнеденко

Величина выборочного коэффициента вариации:

По данным приложения таблица П1,2:

Таблица 5

№

Xi

10³ км

fi

шт

xi/a

a* φ(xi)

φ(xi)

10^-6

fi’

шт

1

38,86

16

0,246

0,6944

4,4017

15,81

0,00

2

83,77

26

0,531

0,7197

4,5618

16,39

5,63

3

128,68

8

0,816

0,6085

3,8567

13,86

2,48

4

173,59

10

1,100

0,4637

2,9393

10,56

0,03

5

218,50

5

1,385

0,3293

2,0870

7,50

0,83

6

263,41

5

1,670

0,2213

1,4029

5,04

0,00

7

308,32

4

1,954

0,1422

0,9014

3,24

0,18

8

353,23

4

2,239

0,0879

0,5570

2,00

2,00

9

398,14

2

2,524

0,0525

0,3325

1,19

0,54

ИТОГО:

80

75,60

11,69

Рис. 5

Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и = 12,592.

Так как χ² > χ_0,05², то эмпирическая выборка значений пренадлежит закону распределения Вейбулла - Гнеденко

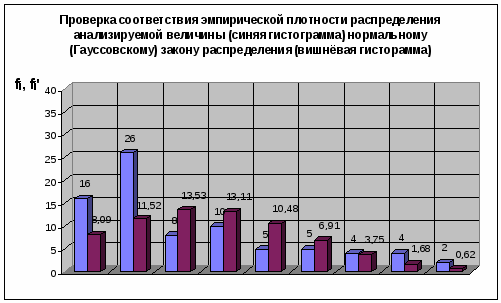
Нормальный (Гауссовский) закон распределения

Таблица 6

№

Xi

10³ км

fi

ti

φ(ti)

10^-2

φ(xi)

fi’

щт

1

38,86

16

-1,025

0,231

0,101

8,09

7,72

2

83,77

26

-0,586

0,328

0,144

11,52

18,18

3

128,68

8

-0,147

0,386

0,169

13,53

2,26

4

173,59

10

0,292

0,374

0,164

13,11

0,74

5

218,50

5

0,731

0,298

0,131

10,48

2,86

6

263,41

5

1,169

0,197

0,086

6,91

0,53

7

308,32

4

1,608

0,107

0,047

3,75

0,02

8

353,23

4

2,047

0,048

0,021

1,68

3,18

9

398,14

2

2,486

0,018

0,008

0,62

3,04

ИТОГО:

80

69,71

38,54

Рис. 6

Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и = 12.592.

Так как χ² > χ_0,05², то гипотеза о принадлежности эмпирической выборки значений, нормальному (Гауссовскому) закону распределения отвергается

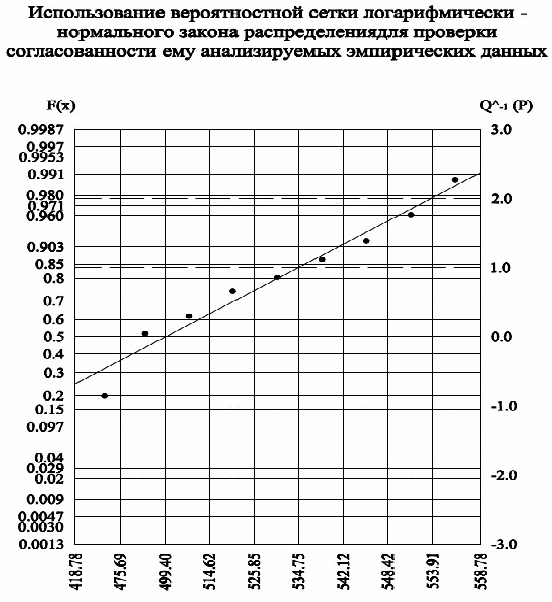
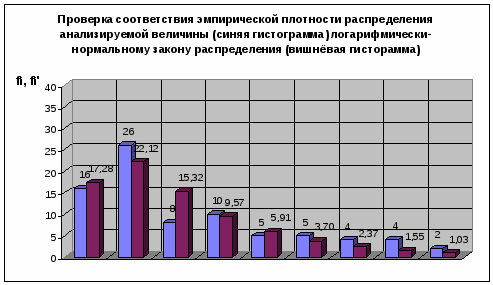
Логарифмически - нормальный закон распределения

Значения средне-выборочное и средне-квадратичное:

Таблица 7

№

Xi

10³ км

fi

ti

φ(ti)

φ(xi)

fi’

щт

1

38,86

16

-1,481

0,133

4,808

17,28

0,094

2

83,77

26

-0,404

0,367

6,155

22,12

0,682

3

128,68

8

0,198

0,391

4,263

15,32

3,494

4

173,59

10

0,618

0,329

2,663

9,57

0,019

5

218,50

5

0,941

0,256

1,645

5,91

0,140

6

263,41

5

1,203

0,193

1,030

3,70

0,455

7

308,32

4

1,423

0,144

0,659

2,37

1,126

8

353,23

4

1,614

0,108

0,430

1,55

3,892

9

398,14

2

1,782

0,081

0,287

1,03

0,908

ИТОГО:

80

10,81

Рис. 7

Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и = 12.592.

Так как χ² < χ_0,05², то эмпирическая выборка значений принадлежит логарифмически-нормальному закону распределения

4. Определение вида теоретического закона распределения случайной величины графическими методами

Расчёт координат эмпирических точек заданной выборки

Таблица 8.

№ п/п

Среднее значение

интервала x_i , 10³ км

f_i , шт

Σ f_i

F(x)= Σ f_i/n+1

1

38,86

16

16

0,198

2

83,77

26

42

0,519

3

128,68

8

50

0,617

4

173,59

10

60

0,741

5

218,50

5

65

0,802

6

263,41

5

70

0,864

7

308,32

4

74

0,914

8

353,23

4

78

0,963

9

398,14

2

80

0,988

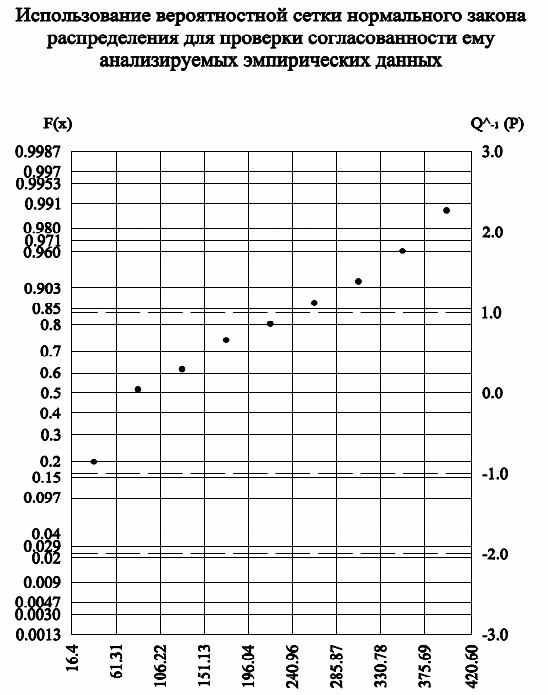
Используя полученные в табл.4. данные, строим вероятностную сетку и выполняем проверку согласованности.

Выбор масштаба построения вероятностной сетки:

• ширина графика (ось абсцисс) А = 140 мм ;

• высота графика (ось ординат) Н = 180 мм .

Нормальный закон распределения

Масштаб значений оси абсцисс устанавливается на основе выражения:

Таблица 9

P = F(x)

0,5

0,6

0,7

0,8

0,8413

0,85

0,903

y = Q^-1(P)

0

0,25

0,52

0,85

1

1,05

1,3

Ky (P), мм

0

7,5

15,6

25,5

30

31,5

39

P = F(x)

0,96

0,971

0,98

0,991

0,9953

0,997

0,9987

y = Q^-1(P)

1,75

1,9

2,05

2,35

2,6

2,75

3

Ky(P), мм

52,5

57

61,5

70,5

78

82,5

90

Лгарифмически - нормальный закон распределения

Масштаб значений оси абсцисс устанавливается на основе выражения:

Таблица 10

№

Границы интервала

xi

10³ км

1

418,78…475,69

38,86

456,01

0,198

2

475,69…499,40

83,77

489,15

0,519

3

499,40…514,62

128,68

507,68

0,617

4

514,62…525,85

173,59

520,60

0,741

5

525,85…534,75

218,50

530,52

0,802

6

534,75…542,12

263,41

538,59

0,864

7

542,12…548,42

308,32

545,38

0,914

8

548,42…553,91

353,23

551,25

0,963

9

553,91…558,78

398,14

556,42

0,988

Экспоненциальный (нормальный) закон распределения

Таблица 11

P = F(x)

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

Ky (P), мм

0,0

3,2

6,7

10,7

15,3

20,8

27,5

36,1

P = F(x)

0,8

0,9

0,95

0,97

0,98

0,99

0,995

0,9975

Ky(P), мм

48,3

69,1

89,9

105,2

117,4

138,2

158,9

179,7

Распределение Вейбулла – Гнеденко

Таблица 12

P = F(x)

0,03

0,04

0,06

0,1

0,2

0,3

0,4

y = Q^-1(P)

-3,5

-3,2

-2,8

-2,25

-1,5

-1,03

-0,7

Ky (P), мм

-118,8

-108,6

-95,0

-76,4

-50,9

-35,0

-23,8

P = F(x)

0,5

0,632

0,78

0,9

0,97

0,955

0,999

y = Q^-1(P)

-0,36

0,00

0,41

0,83

1,25

1,66

1,93

Ky(P), мм

-12,2

0,00

13,9

28,2

42,4

56,3

65,5