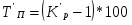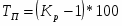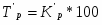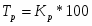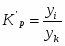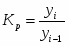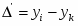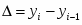ЗАДАЧА 1

По годовым отчетам промышленных предприятий района получена следующая информация:

Номер предприятия

Объем продукции, млн. руб.

Среднегодовая стоимость основных производственных фондов, млн. руб.

1

134,4

7,2

2

264

11,6

3

372

15,6

4

145

7,6

5

427

16,0

6

585

22,0

7

170

8,4

8

464

18,8

9

180

9,2

10

308

13,2

11

586

21,0

12

338

14,0

13

480

19,0

14

240

11,0

15

362

14,8

16

603

23,0

17

375

15,6

18

216

10,0

19

572

19,8

20

277

12,4

Сгруппируйте предприятия по объему выработанной продукции, выделив четыре группы с равными интервалами. По каждой группе определите:

1. Число предприятий;

2. Объем продукции – в целом по группе и в среднем на 1 предприятие;

3. Стоимость основных производственных фондов – в целом по группе и в среднем на 1 предприятие.

Решение оформите в виде статистической таблицы. Сделайте выводы.

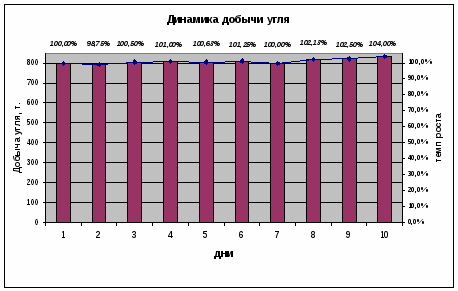
Изобразите ряд распределения предприятий по объему продукции графически в виде гистограммы распределения.

Решение

Ранжируем ряд по объему выработанной продукции

Номер предприятия

Объем продукции, млн. руб.

Среднегодовая стоимость основных производственных фондов, млн. руб.

1

134,4

7,2

4

145

7,6

7

170

8,4

9

180

9,2

18

216

10

14

240

11

2

264

11,6

20

277

12,4

10

308

13,2

12

338

14

15

362

14,8

3

372

15,6

17

375

15,6

5

427

16

8

464

18,8

13

480

19,0

19

572

19,8

6

585

22

11

586

21

16

603

23

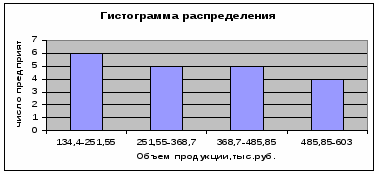
При построении ряда с равными интервалами величина интервала h определяется по формуле

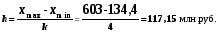
где 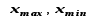– наибольшее и наименьшее значения признака в исследуемой совокупности, k- число групп интервального ряда.

Сгруппируем данные

Границы интервалов

Число предприятий

Объем продукции (млн. руб.)

Среднегодовая стоимость фондов (млн. руб.)

В сумме

В среднем на 1 предприятие

В сумме

В среднем на 1 предприятие

% к объему

134,4-251,55

6

1085,4

180,9

53,4

8,9

4,92%

251,55-368,7

5

1549

309,8

66,0

13,2

4,26%

368,7-485,85

5

2118

423,6

65,5

13,1

3,09%

485,85-603

4

2346

586,5

85,8

21,45

3,66%

Σ

20

7098,4

1500,8

270,7

56,65

15,93%

Как мы видим из таблицы и диаграммы, частота распределения предприятий по объему выработанной продукции имеет тенденцию к снижению, более часто встречаются предприятия с объемом выработанной продукции от 134,4 до 251,55 млн.руб. Также мы видим, что с ростом объема выработанной продукции, уменьшается среднегодовая стоимость фондов (с 4,92% к объему выработанной продукции в первой группе до 3,66% к объему выработанной продукции в четвертой группе)

Рис.1

ЗАДАЧА 2

Методом механического отбора проведено 5 % обследование веса расфасованного груза (мешки муки). Распределение 60 отобранных мешков по весу дало следующие результаты:

Вес мешка, кг.

Число мешков

До 45

3

45-50

6

50-55

40

55-60

7

60-и более

4

Итого:

60

Определите:

1. средний вес одного мешка муки в выборке;

2. размах вариации;

3. среднее линейное отклонение;

4. дисперсию;

5. среднее квадратическое отклонение;

6. коэффициент вариации.

7. с вероятностью 0,997 пределы, в которых может быть гарантирован средний вес мешка муки во всей партии.

Сделайте выводы.

Решение:

Рассчитаем характеристики ряда распределения. Середины крайних (открытых) интервалов определим, исходя из гипотезы равнонаполненности интервалов.

Для расчетов составим вспомогательную таблицу:

Количество изделий за смену, шт.

Середина интервала,

х_i

Частота,

f_i

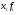
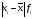
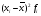
До 45

42,5

3

127,5

30,75

315,1875

45-50

47,5

6

285

31,5

165,375

50-55

52,5

40

2100

10

2,5

55-60

57,5

7

402,5

33,25

157,9375

60-и более

62,5

4

250

39

380,25

Σ

60

3165

144,5

1021,25

1. Для расчета средней дневной выработки рабочих воспользуемся формулой средневзвешенного:

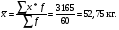
2. Размах вариации равен:

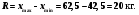
3. Среднее линейное отклонение определим по формуле:

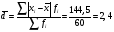
4. Дисперсию найдем по формуле:

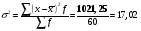
5. Соответственно, среднеквадратическое отклонение равно:

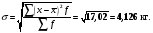
6. Вычислим коэффициент вариации

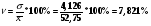
Коэффициент вариации значительно меньше 33% – совокупность достаточно однородна.

1. Определим возможные границы, в которых ожидается среднедневная выработка изделий в генеральной совокупности рабочих. По условию n = 100, тогда N – размер совокупности равен:

N = 60*100% /5% = 1200 шт.

Используем формулы для бесповторного отбора:

Предельная ошибка выборки равна:

,

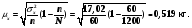т.е. ошибка выборки для средней величины составляет 0,519 кг.

Установим предельные значения для генеральной средней с вероятностью 0,997, учитывая, что вероятности 0,954 соответствует значение коэффициента доверия t=3:

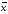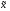
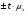== 52,75 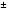3* 0,519 , или 52,23 кг ≤ 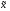≤ 53,27 кг

Таким образом, с вероятностью 99,7%, средний вес мешка муки во всей партии может быть га рантирован в пределах от 52,23 до 53,27 кг.

ЗАДАЧА 3

Имеются следующие данные о продаже картофеля по двум рынкам города:

Рынок

Цена за 1 кг, руб.

Продано картофеля, т

I квартал

II квартал

I квартал

II квартал

1

12

10

5

8

2

11,5

9,5

7

10

3

14

11

4,5

6

Определите:

1. Индивидуальные индексы цен.

2. Индекс цен переменного состава.

3. Индекс цен фиксированного состава.

4. Индекс влияния структурных сдвигов.

Решение

Индивидуальные индексы цен

i_p1=10/2=0,83=83,3% (снижение на 16,7%)

i_p2=9,5/11,5=0,83=82,6% (снижение на 17,4%)

i_p3=11/14=0,79=78,6% (снижение на 21,4%)

Составим вспомогательную таблицу

Рынок

Цена за 1 кг, руб.

Продано картофеля, т

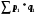
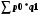
I квартал

II квартал

I квартал

II квартал

1

12

10

5

8

60

80

96

2

11,5

9,5

7

10

80,5

95

115

3

14

11

4,5

6

63

66

84

Сумма

16,5

24

203,5

241

295

На изменение средних цен влияют два фактора:

- цена единицы продукции на рынке

- структура выпуска продукции

Совместное влияние факторов на изменение средней цены картофеля учитывает индекс переменного состава.

Он представляет собой соотношение двух средних величин, т.е. здесь учитываются и структурные изменения в составе совокупности, и изменение качественного признака у отдельных объектов.

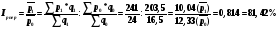
Средняя цена снизилась на 18,58% за счет совместного действия двух факторов

В абсолютном выражении это

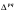=(10,04-12,33)=-2,29 р.

Т.е. средняя стоимость 1 кг картофеля снизилась на 2,29 руб.

Изменение за счет качественного признака учитывает индекс фиксированного (постоянного) состава

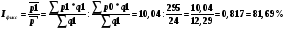
Средняя стоимость 1 кг картофеля снизилась на 18,31% за счет изменения единицы продукции на каждом рынке.

В абсолютном выражении это

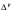= (10,04-12,29)= -2,25 руб.

Изменение структуры выпуска продукции (т.е. изменение доли предприятий в общем выпуске продукции) учитывает индекс структурных сдвигов.

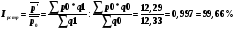
Средняя цена картофеля снизилась на 0,34% за счет изменения структуры продажи картофеля.

В абсолютном выражении это

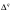=(12,29-12,33)= 0,04 руб.

Взаимосвязь системы индексов:

I_пер=I_фикс*I_стр.

0,814=0,817*0,997

Общий вывод: если бы произошедшие изменения стоимости картофеля не сопровождались структурными изменениями в ее выпуске, то средняя стоимость снизилась бы на 18,31% (на 2 руб. 25 коп.). Изменение структуры продаж на рынках в общем объеме продаж вызвало снижение стоимости на 0,34% (4 коп.). Одновременное воздействие обоих факторов снизило среднюю стоимость 1 кг картофеля на 18,58%, или 2 руб. 29 коп.

ЗАДАЧА 4

Имеются следующие данные о ежесуточной добыче угля по шахте за первую декаду:

День

1

2

3

4

5

6

7

8

9

10

Добыча угля, т.

800

790

804

808

805

810

800

817

820

832

Для анализа динамики добычи угля по шахте определить:

1. абсолютные приросты, темпы роста и прироста добычи угля (базисные и цепные);

2. абсолютное значение 1 % прироста.

3. среднемесячный темп роста и прироста, средний абсолютный прирост (двумя способами);

4. ожидаемый объем добычи угля на 11 день при условии, что среднемесячные темпы с 1 по 10 день сохранятся на 11 день.

Полученные результаты представьте в табличной форме. На основе базисных темпов роста изобразите графически динамику добычи угля.

Сделайте выводы.

Решение:

Показатели динамики

Добыча угля,

т.

Абсолютный прирост,

Δ, т.

Коэффициент роста,

Кр

Темп роста,

Тр, %

Темп прироста,

Тп, %

Абсолютное значение 1% прироста, А_i

С переменной

базой

С постоянной

базой

С переменной

базой

С постоянной

базой

С переменной

базой

С постоянной

базой

С переменной

базой

С постоянной

базой

С переменной

базой

дни

значение

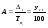
1

800

2

790

-10,00

-10,00

0,99

0,99

98,75%

98,75%

-1,25%

-1,25%

8,00

3

804

14,00

4,00

1,02

1,01

101,77%

100,50%

1,77%

0,50%

7,90

4

808

4,00

8,00

1,00

1,01

100,50%

101,00%

0,50%

1,00%

8,04

5

805

-3,00

5,00

1,00

1,01

99,63%

100,63%

-0,37%

0,63%

8,08

6

810

5,00

10,00

1,01

1,01

100,62%

101,25%

0,62%

1,25%

8,05

7

800

-10,00

0,00

0,99

1,00

98,77%

100,00%

-1,23%

0,00%

8,10

8

817

17,00

17,00

1,02

1,02

102,13%

102,13%

2,13%

2,13%

8,00

9

820

3,00

20,00

1,00

1,03

100,37%

102,50%

0,37%

2,50%

8,17

10

832

12,00

32,00

1,01

1,04

101,46%

104,00%

1,46%

4,00%

8,20

Средние показатели динамики

Показатель

Средний

Абсолютный прирост, т.

Средний

Коэффициент рост

Средний

Темп роста, %

Средний

Темп прироста, %

Средняя величина

абсолютного значения 1% прироста

Метод расчета

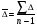
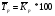0

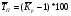
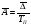
Значение

3,56

1,004

100,44%

0,44%

8,14

Рассчитаем ожидаемый объем добычи угля на 11 день при условии, что среднемесячные темпы роста с 1 по 10 день сохранятся на 11 день.

;

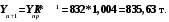На основании рассмотренных данных мы видим, что темп роста добычи угля за рассматриваемый период колеблется. За десять дней лет темп прироста составил 4%. Средний коэффициент роста составил около 1,004 раза, что соответствует среднему приросту в день 0,44%. Средний абсолютный прирост составил 3,56 т. в день.

ЗАДАЧА 5

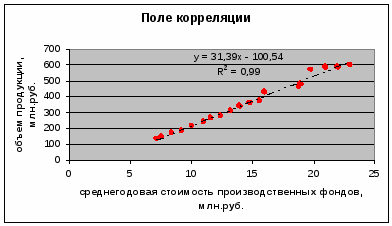
По данным задачи 1 найдите уравнение корреляционной связи между факторным (х) и результативным (у) признаками. Проанализируйте параметры уравнения регрессии. Для оценки тесноты связи между признаками исчислите линейный коэффициент корреляции и коэффициент детерминации. Изобразите корреляционную связь графически.

Решение:

Найдем уравнение линейной регрессии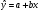

Заполним вспомогательную таблицу:

Таблица

x

y

х²

y²

хy

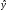
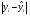
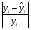
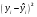
7,2

134,4

51,84

18063,36

967,68

125,46

8,94

0,067

79,88

7,6

145

57,76

21025

1102

138,02

6,98

0,048

48,75

8,4

170

70,56

28900

1428

163,13

6,87

0,040

47,20

9,2

180

84,64

32400

1656

188,24

8,24

0,046

67,92

10

216

100

46656

2160

213,35

2,65

0,012

7,01

11

240

121

57600

2640

244,74

4,74

0,020

22,49

11,6

264

134,56

69696

3062,4

263,58

0,42

0,002

0,18

12,4

277

153,76

76729

3434,8

288,69

11,69

0,042

136,61

13,2

308

174,24

94864

4065,6

313,80

5,80

0,019

33,64

14

338

196

114244

4732

338,91

0,91

0,003

0,83

14,8

362

219,04

131044

5357,6

364,02

2,02

0,006

4,09

15,6

372

243,36

138384

5803,2

389,13

17,13

0,046

293,59

15,6

375

243,36

140625

5850

389,13

14,13

0,038

199,79

16

427

256

182329

6832

401,69

25,31

0,059

640,57

18,8

464

353,44

215296

8723,2

489,58

25,58

0,055

654,40

19

480

361

230400

9120

495,86

15,86

0,033

251,51

19,8

572

392,04

327184

11325,6

520,97

51,03

0,089

2603,99

22

585

484

342225

12870

590,03

5,03

0,009

25,28

21

586

441

343396

12306

558,64

27,36

0,047

748,67

23

603

529

363609

13869

621,42

18,42

0,031

339,20

290,20

7098,40

4666,60

2974669,36

117305,08

7098,40

259,12

0,710

6205,59

Определим коэффициенты регрессии:

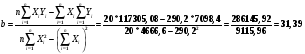
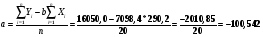
Уравнение имеет вид: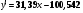

С увеличением среднегодовой стоимости производственных фондов на 1 млн.руб. объем продукции увеличивается на 31,39 млн.руб. в среднем.

Оценим качество уравнения с помощью средней ошибки аппроксимации по формуле:

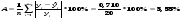
Допустимый предел значений A – не более 8 – 10%.

В рассматриваемом случае в среднем расчетные значения отклоняются от фактических в допустимых пределах. Качество уравнения регрессии можно оценить как хорошее.

Определим коэффициент корреляции (воспользуемся вспомогательной таблицей):

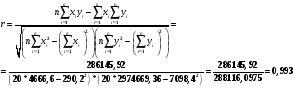
Коэффициент детерминации: r² = 0,986

Соответственно 98,6% изменения фактора y объясняется изменением фактора x.

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем t-критерий Стьюдента по формуле:

Вычисленное t-значение сравним с табличным (критическим) значением при принятом уровне значимости а = 0,05 и числе степеней свободы v = n - 2 = 20-2 = 18.

Табличное значение по таблице распределения Стьюдента равно 2,101.

Фактическое значение критерия больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и наличии линейной связи между факторами.

Оценим значимости уравнения регрессии и показателя тесноты связи с помощью F-критерия Фишера. Для этого сравним его фактическое значение F_факт с табличным (критическим) значением F_табл.

Фактическое значение F_факт рассчитаем по формуле:

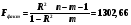
Табличное значение F_табл по таблице значений F-критерия Фишера при а = 0,05, n =20, m = 1 (т - число параметров при переменной х) равно:

F_(0,05;1;18) = 4,414

Фактическое значение критерия больше табличного, что свидетельствует о статистической значимости уравнения регрессии в целом и показателя тесноты связи r_ху.

Рис.1

На графике корреляционного поля видно, что между показателями наблюдается хорошо выраженная прямая положительная зависимость (с увеличением стоимости основных производственных фондов увеличивается объем выпущенной продукции). Что также подтверждается теоретическими расчетами.

ЗАДАЧА 6

Численность занятых, безработных и экономически активного населения Волгоградской области характеризуется данными (тыс. человек):

Год

численность

занятые

безработные

экономически активное

2001

938,0

159,0

1097,0

2002

1079,3

153,7

1233,0

Определить:

1. уровни безработицы, уровни занятости;

2. темпы роста и прироста исчисленных показателей.

Сделайте выводы.

Решение.

Уровень безработицы – это удельный вес безработных в численности экономически активного населения

Уровень безработицы = Численность безработных / Численность экономически активного населения *100%.

Уровень занятости = Численность занятых / Численность экономически активного населения * 100%.

Уровень занятости характеризует степень использования трудоспособного населения в сфере общественно полезного труда.

Составим таблицу

Уровень

Год

Темпы роста/прироста

2001

2002

Темп роста

Темп прироста

занятости

85,5%

87,5%

1,02

0,02

безработицы

14,5%

12,5%

0,86

0,14

Выводы

В период за 2001-2002 год в области увеличился процент занятости, то есть увеличилась степень использования трудоспособного населения с 85,5% до 87,5%. Темп прироста этого показателя составил 2%. Уровень безработицы понизился и составил 12,5% в 2002 году по сравнению с 14,5% в 2001 году. То есть темп прироста (снижения) этого показателя составил 14%.

ЗАДАЧА 7

Выполнить анализ факторов, влияющих на объем выпуска продукции хлебозавода, на основе следующих данных (среднегодовой стоимости основных фондов и фондоотдачи):

Показатели

Базисный год

Отчетный год

в сопоставимых ценах

Объем товарной продукции, тыс. руб.,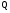

12455

13248

Среднегодовая стоимость основных фондов, тыс. руб.,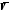

6120

6220

Решение:

Определим фондоотдачу и составим таблицу:

Показатели

Базисный год

Отчетный год

в сопоставимых ценах

Объем товарной продукции, тыс. руб.,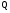

12455

13248

Среднегодовая стоимость основных фондов, тыс. руб.,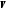

6120

6220

Фондоотдача,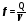

Влияние каждого фактора на изменение объема товарной продукции найдем методом цепных подстановок.

Сущность метода цепных подстановок заключается в последовательной замене отчетной величины факториальных показателей базисной величиной этих показателей или, наоборот, в последовательной замене базисной величины факториальных показателей отчетной и определение влияния этой замены на результативный показатель.

Влияние качественного фактора определяется при фактической величине количественного фактора, влияние количественного фактора, наоборот, определяется по базисной величине качественного фактора.

Введем обозначения:

Q₀ и Q₁ – результативный показатель базисного и отчетного периода;

V₀, f₀ – факториальные показатели базисного периода;

V₁, f₁ – то же, отчетного периода.

Тогда, общее изменение объема товарной продукции:

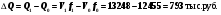
Изменение объема товарной продукции под влиянием изменения среднегодовой стоимости основных фондов:

;

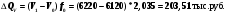Изменение объема товарной продукции под влиянием изменения показателя фондоотдачи:

;

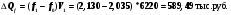Проверим результат расчета:

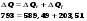
Используемая литература

1. Экономическая статистика: Учебник / Под ред. Ю.Н. Иванова – М.:ИНФРА-М, 1999. – 480 с.