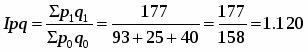
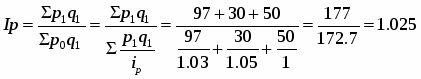
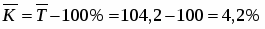
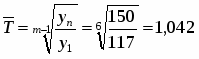
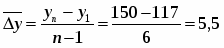
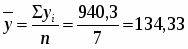
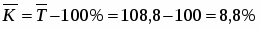
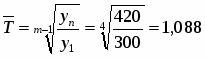
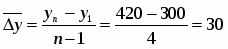
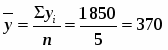
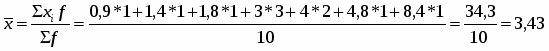
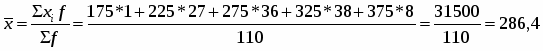
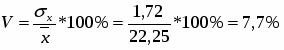
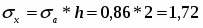
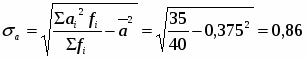
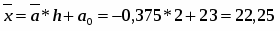
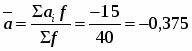
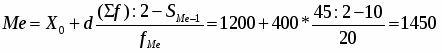
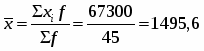
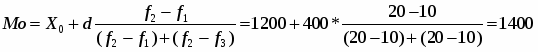
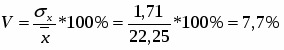
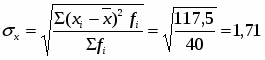
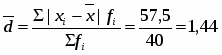
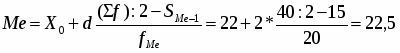
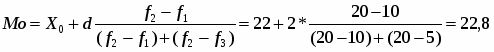
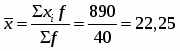
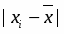
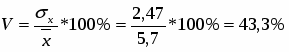
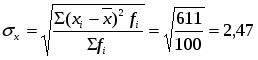
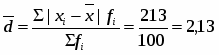
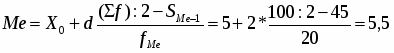
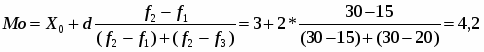
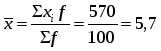
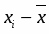
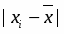
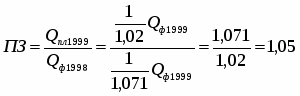
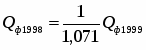
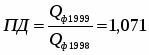
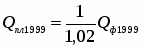
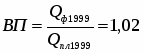
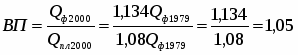
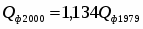
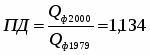
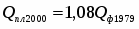
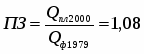Задача 1.

Плановое задание по реализации продукции на 2000г. составляет 108% показатель динамики за 2000г. по сравнению с 1979г. - 113,4%. На сколько процентов выполнен план по реализации продукции в 2000г.

Решение:

Плановое задание по реализации продукции на 2000г.:

,

значит

Показатель динамики за 2000г. по сравнению с 1979г.:

, значит

Вычислим процент выполнения плана по реализации продукции в 2000г.:

, или 105%

Значит план по реализации продукции в 2000г. перевыполнили на 5%.

Задача 2.

Численность населения и число построенных квартир в двух районах характеризуются следующими данными:

Район

Число построенных квартир, тыс. шт.

Численность населения, млн. чел.

1990г.

2000г.

1990г.

2000г.

А

Б

107

208

233

180

18

15

25

21

Вычислите все возможные относительные величины. Укажите к какому виду они относятся. За базу сравнения примите уровень Б.

Решение:

Динамика числа построенных квартир:

- район А 233 / 107 = 2,178 или 217,8%

- район Б 180 / 208 = 0,865 или 86,5%.

Динамика численности населения:

- район А 25 / 18 = 1,389 или 138,9%

- район Б 21 / 15 = 1,4 или 140%.

Коэффициент координации числа построенных квартир в районе А к району Б:

- 1990г. 107 / 208 = 0,514 или 51,4%

- 2000г. 233 / 180 = 1,294 или 129,4%

Коэффициент координации численности населения в районе А к району Б:

- 1990г. 18 / 15 = 1,2 или 120%

- 2000г. 25 / 21 = 1,190 или 119%

Задача 3.

План роста производительности труда на 1999г. выполнен предприятием на 102%, показатель динамики производительности труда за 1999г. по сравнению с 1998г. – 107,1%. Определите плановое задание по росту производительности труда на 1999г.

Решение:

План роста производительности труда на 1999г.:

, значит

Показатель динамики производительности труда за 1999г. по сравнению с 1998г.:

, значит

Плановое задание по росту производительности труда на 1999г.:

или 105%

Значит плановое задание по росту производительности труда на 1999г. составило 105%.

Задача 4.

Группы предприятий по размеру основных фондов, млн. руб.

1 - 3

3 - 5

5 - 7

7 - 9

Более 9

Число предприятий в % к итогу

15

30

20

25

10

Найти средний размер основных фондов, моду и медиану, дисперсию, среднее линейное и среднее квадратическое отклонение, коэффициент вариации.

Решение:

Построим вспомогательную таблицу:

Группы предприятий по размеру основных фондов, млн. руб.

Середина интервала, х_i

Число предприятий в % к итогу, f_i

х_i f_i

f_i

()²f_i

1 – 3

2

15

30

55,5

205,35

3 – 5

4

30

120

51

86,7

5 – 7

6

20

120

6

1,8

7 – 9

8

25

200

57,5

132,25

Более 9

10

10

100

43

184,9

Итого:

-

100

570

213

611

Средний размер основных фондов

(млн. руб.)

Мода размера основных фондов:

(млн. руб.)

Значит большинство предприятий имеет размер основных фондов 4,2 млн. руб.

Медиана размера основных фондов:

(млн. руб.)

Значит 50% предприятий имеют размер основных фондов менее 5,5 млн. руб., а 50% - более 5,5 млн. руб.

Среднее линейное отклонение размера основных фондов:

(млн. руб.)

Среднее квадратическое отклонение размера основных фондов:

(млн. руб.)

Коэффициент вариации:

> 33%,

значит совокупность предприятий по размеру основных фондов считать однородной нельзя.

Задача 5

Группы рабочих по возрасту, лет

Число рабочих, чел.

18 – 20

5

20 – 22

10

22 – 24

20

Более 24

5

Найти средний возраст одного рабочего, моду медиану и коэффициент вариации.

Решение:

Построим вспомогательную таблицу:

Группы рабочих по возрасту, лет

Середина интервала, х_i

Число рабочих, f_i

х_i f_i

f_i

()²f_i

18 – 20

19

5

95

16,25

52,8125

20 – 22

21

10

210

12,5

15,625

22 – 24

23

20

460

15

11,25

Более 24

25

5

125

13,75

37,8125

Итого:

-

40

890

57,5

117,5

Средний возраст одного рабочего

(лет)

Мода возраста одного рабочего:

(лет)

Значит возраст большинства рабочих составляет 22,8 лет.

Медиана возраста одного рабочего:

( лет)

Значит возраст 50% рабочих менее 22,5 лет, а других 50% - более 22,5 лет.

Среднее линейное возраста одного рабочего:

(лет)

Среднее квадратическое отклонение возраста одного рабочего:

(лет)

Коэффициент вариации:

< 33%,

значит совокупность рабочих по возрасту можно считать однородной.

Задача 6

Группы рабочих по размеру зарплаты, руб.

Число рабочих, чел.

800 – 1200

10

1200 – 1600

20

1600 – 2000

10

Более 2000

5

Определить моду и коэффициент асимметрии.

Решение:

Мода заработной платы одного рабочего:

(руб.)

Значит зарплата большинства рабочих составляет 1400 руб.

Группы рабочих по размеру зарплаты, руб.

Середина интервала, х_i

Число рабочих, f_i

х_i f_i

Накопленная частота

800 – 1200

1000

10

10000

10

1200 – 1600

1400

20

28000

30

1600 – 2000

1800

10

18000

40

Более 2000

2200

5

11000

45

Итого:

-

45

67300

-

Средний размер заработной платы одного рабочего

(руб.)

Медиана возраста одного рабочего:

(руб.)

Если M₀ < Me < имеет место правосторонняя асимметрия, если же < Me <M₀ - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что асимметрия – правосторонняя.

Задача 7

Группы студентов по возрасту, лет

Число студентов, чел.

18 – 20

5

20 – 22

10

22 – 24

20

Более 24

5

Найти средний возраст одного студента, используя метод моментов, среднеквадратическое отклонение и коэффициент вариации.

Решение:

Построим вспомогательную таблицу:

Группы рабочих по возрасту, лет

Середина интервала, х_i

Условная варианта

а_i

Число рабочих, f_i

а_i f_i

а_i²f_i

18 – 20

19

-2

5

-10

20

20 – 22

21

-1

10

-10

10

22 – 24

23

0

20

0

0

Более 24

25

1

5

5

5

Итого:

-

-

40

-15

35

Найдем средний возраст студентов:

Тогда

(лет)

Найдем среднее квадратическое отклонение:

Тогда

(лет)

Коэффициент вариации:

< 33%,

значит совокупность студентов по возрасту можно считать однородной.

Задача 8.

Имеются данные о среднегодовой стоимости ОФ двух пароходств АО»Волга-флот» и Ленское объединение речное пароходство.

Ао «Волга-флот№»

АО «ЛОРП»

Группы предприятий по среднегодовой стоимости ОПФ, млн. руб.

Количество предприятий в % к итогу

Группы предприятий по среднегодовой стоимости ОПФ, млн. руб.

Количество предприятий в % к итогу

До 200

2

До 200

1

200 – 220

12

200 – 250

27

220 – 240

24

250 – 300

36

240 – 260

22

300 – 350

38

260 – 280

18

Свыше 350

8

280 – 300

9

300 – 320

11

320 – 340

10

Свыше 340

2

Итого:

110

110

1. Проведите вторичную группировку предприятий АО «Волга-флот» по среднегодовой стоимости ОПФ (по величине интервала АО «ЛОРП»).

2. Рассчитайте среднегодовую стоимость ОПФ АО «Волга-флот» и АО «ЛОРП».

3. Выполните сравнительный анализ полученных результатов по двум пароходствам.

Решение:

1. Проведением вторичную группировку предприятий АО «Волга-флот» по среднегодовой стоимости ОПФ (по величине интервала АО «ЛОРП»).

Ао «Волга-флот№»

Группы предприятий по среднегодовой стоимости ОПФ, млн. руб.

Количество предприятий в % к итогу

До 200

2

200 – 250

47

250 – 300

38

300 – 350

22

Свыше 350

1

2. Рассчитаем среднегодовую стоимость ОПФ АО «Волга-флот»:

(млн. руб.)

Рассчитаем среднегодовую стоимость АО «ЛОРП».

(млн. руб.)

3. Видим, что среднегодовая стоимость основных производственных фондов на АО «ЛОРП» превышает среднегодовую стоимость основных фондов на АО «Волга-флот» на 23,7 млн. руб.

Задача 9

Объем реализованной продукции предприятий составил, млн. руб.:

4,0 3,0 8,4 4,8 0,9 1,4 3,0 4,0 1,8 3,0

Требуется:

1. Произвести группировку предприятий по объему реализованной продукции;

2. Составить дискретный ряд;

3. Изобразить ряд графически;

4. Определить накопленные частоты.

Решение:

1. Произведем группировку предприятий по объему реализованной продукции и составим дискретный ряд:

Объем реализованной продукции, млн. руб.

0,9

1,4

1,8

3,0

4,0

4,8

8,4

Итого:

Число предприятий

1

1

1

3

2

1

1

10

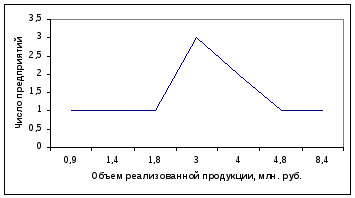
2. Изобразим полученный ряд графически:

2. Определим накопленные частоты:

Объем реализованной продукции, млн. руб.

0,9

1,4

1,8

3,0

4,0

4,8

8,4

Накопленные частоты

1

2

3

6

8

9

10

4. Определим средний объем реализованной продукции:

(млн. руб.)

Задача 10.

Объем валовой продукции предприятий составил, млн. руб.:

4,0 3,0 8,4 4,8 0,9 1,4 3,0 4,0 1,8 3,0

Требуется:

1. Произвести группировку предприятий по объему валовой продукции;

2. Составить интервальный ряд распределения;

3. Изобразить ряд графически;

4. Определить накопленные частоты.

Решение:

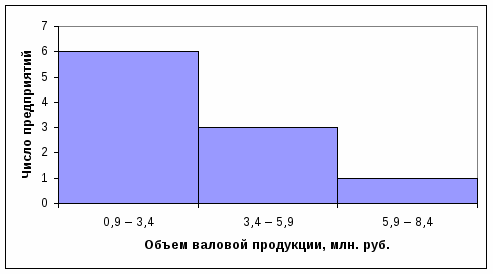
1. Произведем группировку предприятий по объему валовой продукции и составим интервальный ряд распределения:

Объем валовой продукции, млн. руб.

0,9 – 3,4

3,4 – 5,9

5,9 – 8,4

Итого:

Число предприятий

6

3

1

10

2. Изобразим полученный ряд графически:

2. Определим накопленные частоты:

Объем валовой продукции, млн. руб.

0,9 – 3,4

3,4 – 5,9

5,9 – 8,4

Накопленные частоты

6

9

10

Задача 11.

По данным таблицы определить средний годовой темп роста объема перевезенных грузов речным транспортом, абсолютный прирост, темпы роста (цепные, базисные), абсолютное значение 1% прироста. Результаты оформите в виде таблицы. Сделайте выводы.

Год

1994

1995

1996

1997

1998

Перевезено грузов, млн. тонн

300

350

380

400

420

Решение:

Произведем анализ динамики перевозки грузов, вычислив для этого абсолютные и относительные показатели динамики. Результаты представим в таблице.

Годы

1994

1995

1996

1997

1998

Перевезено грузов, млн. т

300

350

380

400

420

Абсолютный прирост, млн. т

- цепной

-

50

30

20

20

- базисный

0

50

80

100

120

Темп роста, %

- цепной

-

116,7

108,6

105,3

105,0

- базисный

100

116,7

126,7

133,3

140,0

Темп прироста, %

- цепной

-

16,7

8,6

5,3

5,0

- базисный

0

16,7

26,7

33,3

40,0

Абсолютное содержание 1% прироста, млн. т

-

3

3,5

3,8

4

Среднегодовой объем перевозок:

(млн. т)

Среднегодовой абсолютный прирост:

(млн. т)

Среднегодовой темп роста:

или 108,8%

Среднегодовой темп прироста:

Таким образом, видим, что в 1994 – 1998г.г. тенденция объема перевозок характеризуется постоянным ростом. В целом за рассматриваемый период объем перевозок увеличился на 120 млн. т или 40%. В среднем объем перевозок в год увеличивался на 30 млн. т или на 8,8%.

Задача 12.

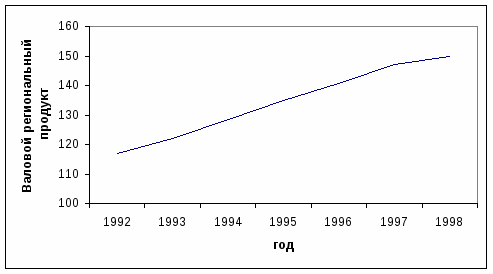
Валовой региональный продукт Нижегородской области за 1992 – 1998 г.г. в сопоставимых ценах характеризуется следующими данными:

Год

1992

1993

1994

1995

1996

1997

1998

Валовой региональный продукт

117,0

122,2

128,6

134,8

140,7

147,0

150,0

Для анализа динамики определите:

1. абсолютные приросты;

2. темпы роста и прироста;

3. среднегодовой уровень;

4. Среднегодовой абсолютный прирост;

5. Среднегодовой темп роста и прироста;

6. Постройте график динамики валового регионального продукта.

Решение:

Произведем анализ динамики перевозки грузов, вычислив для этого абсолютные и относительные показатели динамики. Результаты представим в таблице.

Годы

1992

1993

1994

1995

1996

1997

1998

Перевезено грузов, млн. т

117,0

122,2

128,6

134,8

140,7

147,0

150,0

Абсолютный прирост, млн. т

- цепной

-

5,2

6,4

6,2

5,9

6,3

3

- базисный

0

5,2

11,6

17,8

23,7

30

33

Темп роста, %

- цепной

-

104,4

105,2

104,8

104,4

104,5

102,0

- базисный

100

104,4

109,9

115,2

120,3

125,6

128,2

Темп прироста, %

- цепной

-

4,4

5,2

4,8

4,4

4,5

2,0

- базисный

0

4,4

9,9

15,2

20,3

25,6

28,2

Абсолютное содержание 1% прироста, млн. т

-

1,17

1,222

1,286

1,348

1,407

1,47

Среднегодовой валовой региональный продукт:

Среднегодовой абсолютный прирост:

Среднегодовой темп роста:

или 104,2%

Среднегодовой темп прироста:

Таким образом, видим, что в 1992 – 1998г.г. тенденция валового регионального продукта характеризуется постоянным ростом. В целом за рассматриваемый период валовой региональный продукт увеличился на 33 или 28,2%. В среднем валовой региональный продукт в год увеличивался на 5,5 или на 4,2%.

Изобразим ряд динамики графически:

Задача 13.

Имеются следующие данные по трем товарным группам:

Товарная группа

Товарооборот в мае

p₀q₀

Товарооборот в июне

p₁q₁

Изменение цен в июне по сравнению с маем, %

А

93

97

+3

В

25

30

+5

С

40

50

Без изменения

Определить:

1. общий индекс товарооборота;

2. индивидуальные и общий индексы цен;

3. индивидуальные и общий индексы объема физических продаж;

4. изменение товарооборота за счет изменения цен и объема реализованной продукции.

Решение:

1. Определим индивидуальные индексы: цен, физического объема товарооборота и товарооборота в фактических ценах;

Товарные группы

Индекс цен

Индекс товарооборота в фактических ценах

Индекс физического объема

А

1,03

97 / 93 = 1,043

1,043 / 1,03 = 1,013

В

1,05

25 / 30 = 0,833

0,833 / 1,05 = 0,793

С

1,0

40 / 50 = 0,8

0,8 / 1,0 = 0,8

2. Общий индекс физического объема товарооборота (общий):

или 102,5%

3. Общий индекс товарооборота в фактических ценах:

или 112%

4. Общий индекс физического объема продаж:

Iq = Ipq / Ip = 1,120 / 1,025 = 1,093 или 109,3%

5. Прирост товарооборота:

• всего Δpq = Σ p₁q₁ – Σ p₀q₀ = 177 - 158 = 19

• за счет изменения цен Δpq (р)= 177 – 172,7 = 4,3

• за счет изменения физического объема Δpq (q) = 19 – 4,3 = 14,7

Таким образом, товарооборот по товарным группам вырос на 19 ден. ед или на 12% в июне по сравнению с маем, причем на 14,7 ден. ед. или на 9,3% он вырос за счет увеличения физического объема продаж, а на 4,3 ден. ед. или на 2,5% за счет роста цен.

Список использованной литературы:

1. Гусаров В.М., «Теория статистики», – М.: Аудит, ЮНИТИ, 2002;

2. Ефимова М.П., Петрова Е.В., Румянцев В.Н., «Общая теория статистики», - М.: “Инфра - М”, 2003;

3. «Практикум по статистике: Учеб. пособие для вузов» / Под ред. В.М. Симчеры / ВЗФЭИ. – М.: ЗАО «Финстатинформ», 2000.

2