Статистический анализ производства зерна, сахарной свеклы, подсолнечника

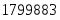
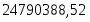
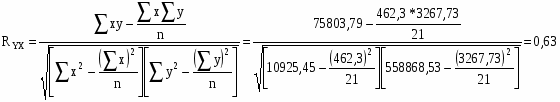
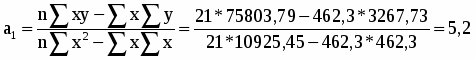
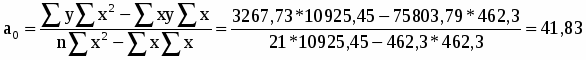
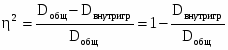
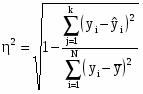
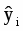
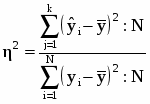
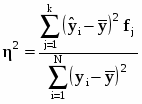
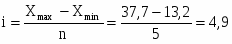
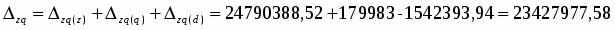
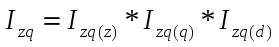
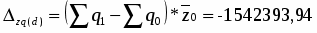
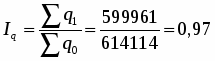
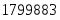
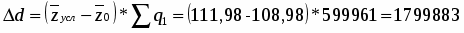
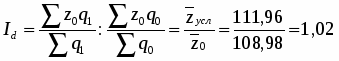
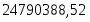
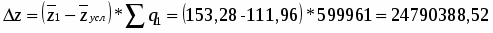
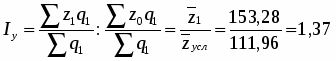
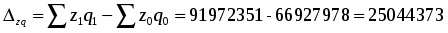
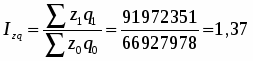
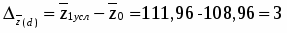
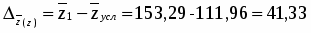
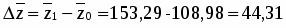
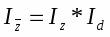
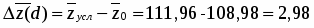
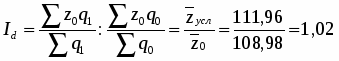
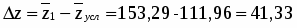
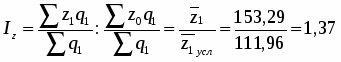
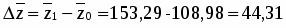
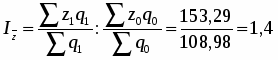
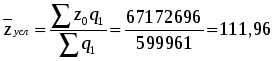
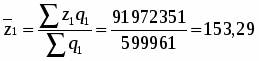
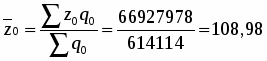
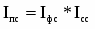
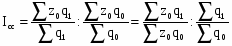
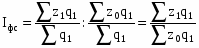
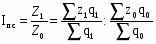
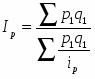
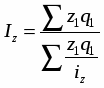
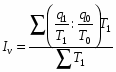
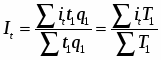
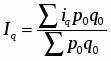
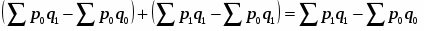
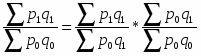
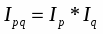
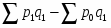
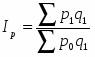
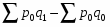
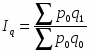
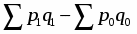
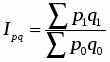
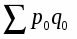
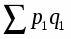
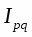
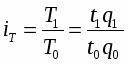
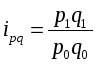
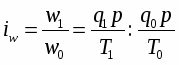
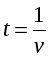
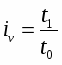
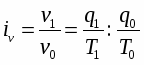
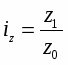
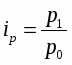
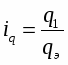
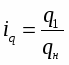
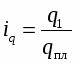
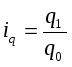
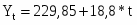
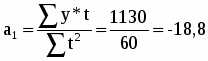
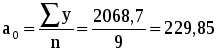
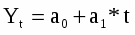
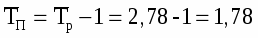
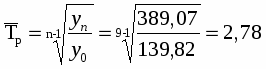
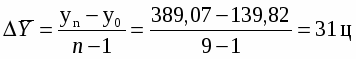
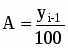
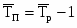
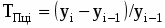
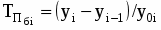
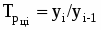
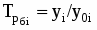
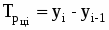
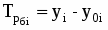Содержание

Введение

1.Анализ рядов динамики

1.1. Показатели себестоимости и производственных затрат, их сущность, методика расчета

1.2. Динамики производственных затрат на производство зерна, сахарной свеклы, подсолнечника за 6 лет

1.3. Динамика себестоимости 1 ц. зерна (сахарной свеклы, подсолнечника). Темпы ее роста и прироста, показатели вариации за 9 лет. Выявление тенденций изменения себестоимости 1 ц. за 9 лет

2. Индексный метод анализа

2.1. Сущность индекса, их виды

2.2. Индексный анализ изменения средней себестоимостии производственны затрат

3.Выявление взаимосвязи методом аналитической группировки

3.1. Сущность группировки, их виды и значение

3.2. Аналитическая группировка хозяйств по одному из факторов (Х- урожайность зерна (сахарной свеклы, подсолнечника), уровень интенсификации), влияющих на себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника)

4.Корреляционно-регрессионный анализ

4.1. Сущность и основные условия применения корреляционного анализа

4.2. Построение однофакторной корреляционной модели зависимости себестоимости 1 ц. от фактора (Х- урожайность зерна, (сахарной свеклы, подсолнечника), Х – производственных затрат)

Выводы и предложения

Список использованной литературы

Введение

Себестоимость 1 ц. и производственные затраты — важнейшие результативные показатели растениеводства и сельскохозяйственного производства в целом. Уровень себестоимости отражает воздействие экономических и приходных условий, в которых осуществляется сельскохозяйственное производство, и качество организационно-хозяйственной деятельности каждого предприятия.

Задачи статистики себестоимости состоят в том, чтобы правильно определить уровни себестоимости и их изменения по сравнению с прошлыми периодами и планом; раскрыть, путем анализа, причины изменений в динамике и факторы, обусловившие различия в уровнях себестоимости между зонами, районами, группами хозяйств; оценить эффективность различных факторов себестоимости; выяснить неиспользованные резервы повышения себестоимости. [19, с. 53]

Актуальность темы данной работы определяется в первую очередь объективно значительной ролью изучения себестоимости в системе АПК в современной социально ориентированной рыночной экономике, переход к коей является главным вектором разворачиваемой в России радикальной реформы.

Курсовая работа содержит материал теоретического и практического значения. Проведен анализ финансовых показателей деятельности сельхоз предприятий.

Целью курсовой работы является статистико-экономический анализ себестоимости и производственных затрат зерна (сахарной свеклы, подсолнечника).

Задачи курсовой работы:

Провести анализ рядов динамики себестоимости и производственных затрат зерна (сахарной свеклы, подсолнечника) за ряд лет;
Проанализировать себестоимости и производственных затрат зерна (сахарной свеклы, подсолнечника) индексным методом;
Провести группировку статистических показателей себестоимости.

Провести корреляционно-регрессионный анализ зависимости себестоимости и производственных затрат зерна (сахарной свеклы, подсолнечника) от урожайности.

1.Анализ рядов динамики

1.1 Показатели урожая и урожайности, их сущность, методика расчета

Себестоимость продукции относится к числу важнейших качественных показателей, в обобщенном виде отражающих все стороны хозяйственной деятельности предприятий (фирм, компаний), их достижения и недостатки. Уровень себестоимости связан с объемом и качеством продукции, использованием рабочего времени, сырья, материалов, оборудования, расходованием фонда оплаты труда и т.д. Себестоимость, в свою очередь, является основой определения цен на продукцию. Снижение ее приводит к увеличению суммы прибыли и уровня рентабельности. Чтобы добиваться снижения себестоимости, надо знать ее состав, структуру и факторы ее динамики. Все это и является предметом статистического изучения при анализе себестоимости. [9, с. 103]

Себестоимость продукции (работ, услуг) представляет собой стоимостную оценку используемых в процессе производства продукции (работ, услуг) природных ресурсов, сырья, материалов, топлива, энергии, основных фондов, трудовых ресурсов и других затрат на ее производство и реализацию.

В себестоимости учитываются затраты прошлого труда, перенесенные на вновь созданную продукцию (сырье, материалы, топливо, электроэнергия, износ основных средств), издержки, связанные с использованием живого труда (оплата труда рабочих и служащих, отчисления на социальные нужды), и прочие затраты. Себестоимость является частью стоимости продукции и показывает, во что обходится производство продукции для предприятия (фирмы).

Необходимо различать общую себестоимость всей произведенной продукции – общую сумму затрат, приходящихся на изготовление продукции определенного объема и состава, и индивидуальную себестоимость – затраты на производство только одного изделия (например, на изготовление уникального агрегата при условии, что в данном производственном звене никаких других видов продукции одновременно не производится) – и среднюю себестоимость, определяемую делением общей суммы затрат на количество произведенной продукции.

В практике статистики различают два основных вида себестоимости по степени учета затрат: производственную и полную.

Производственная себестоимость охватывает только затраты, связанные с процессом производства продукции – начиная с момента запуска сырья в производство и кончая освидетельствованием готовых изделий и сдачей их на склад готовой продукции. [6, с. 211]

Полная себестоимость – это сумма расходов, связанных с производством продукции (производственная себестоимость), и расходов по ее реализации (коммерческие расходы). Коммерческие расходы включают в себя затраты на упаковку, хранение, погрузку, транспортировку и рекламу.

Статистика себестоимости продукции опирается на данные бухгалтерского учета, задачами которого являются определение общей суммы затрат, группировка их по видам и калькулирование себестоимости единицы продукции.

Анализируя данные бухгалтерского учета и отчетности, статистика решает следующие задачи: изучает структуру себестоимости по видам затрат и выявляет влияние изменения структуры на динамику себестоимости:

дает обобщающую характеристику динамики себестоимости продукции;
исследует факторы, определяющие уровень и динамику себестоимости, и выявляет возможности ее снижения.

Среди затрат на производство выделяются следующие элементы:

материальные затраты (за вычетом стоимости возвратных отходов);
затраты на оплату труда;
отчисления на социальные нужды;
амортизация основных фондов;
прочие затраты.

В элементе «Материальные затраты» отражается стоимость:

приобретаемых со стороны сырья и материалов, которые входят в состав вырабатываемой продукции;
покупных материалов, используемых в процессе производства продукции для обеспечения нормального технологического процесса и для упаковки продукции, а также запчастей для ремонта оборудования;
покупных комплектующих изделий и полуфабрикатов, подвергающихся в дальнейшем монтажу или дополнительной обработке на данном предприятии;
работ и услуг производственного характера, выполненных другими предприятиями или производствами того же предприятия, не относящимися к основному виду деятельности;
приобретаемых со стороны топлива и энергии всех видов, расходуемых на технологические цели. [12, с. 179]

Стоимость материальных ресурсов формируется исходя из цен их потребления (без учета НДС), наценок, компенсационных вознаграждений, уплачиваемых снабженческими и внешнеэкономическими организациями, стоимости услуг товарных бирж, включая брокерские услуги, таможенных пошлин, платы за транспортировку, хранение и доставку, осуществляемые другими предприятиями.

Сумма всех указанных выше затрат на сырье и материалы, израсходованная на выпуск продукции, уменьшается на стоимость возвратных отходов производства. Возвратными отходами производства называются возникающие в процессе превращения исходного материала в готовую продукцию остатки сырья и материалов, утерявшие полностью или частично потребительные качества исходного материала, но могущие быть вторично использованы предприятием в качестве материала на выпуск основной продукции или продукции вспомогательных производств либо, наконец, реализованы на сторону. Они оцениваются в зависимости от их качества или по пониженной цене исходного сырья, или по цене лома, обрезков и т.п. В элемент "Затраты на оплату труда" входят:

затраты на оплату труда основного производственного персонала предприятия, включая премии рабочим и служащим за производственные результаты, а также компенсации в связи с повышением цен и индексацией доходов в пределах норм, предусмотренных законодательством;
компенсации, выплачиваемые в установленных законодательством размерах женщинам, находящихся в частично оплачиваемом отпуске по уходу за ребенком до достижения им определенного законодательством возраста.

Элемент «Отчисления на социальные нужды» включает обязательные отчисления по установленным законодательством нормам (органам государственного социального страхования. пенсионного фонда, государственного фонда занятости и т.п.) от сумм затрат на оплату труда (элемент себестоимости продукции «затраты на оплату труда»). [18, с. 56]

В элементе «Амортизация основных фондов» отражается сумма амортизационных отчислений на полное восстановление основных производственных фондов, определяемая исходя из их балансовой стоимости и утвержденных в установленном порядке норм, включая и ускоренную амортизацию их активной части.

К элементу «Прочие затраты» относятся:

износ по нематериальным активам;
арендная плата;
вознаграждения за изобретения и рационализаторские предложения;
обязательные страховые платежи;
проценты по кредитам банков;
суточные и подъемные;
налоги, включаемые в себестоимость продукции (работ, услуг);
отчисления во внебюджетные фонды;
оплата услуг рекламных агентов и аудиторских организаций, связи, вычислительных центров, вневедомственной охраны и др.

Таким образом, поэлементный анализ себестоимости показывает, каковы конкретно расходы на производство продукции, независимо от их места и непосредственного назначения.

Распределение затрат по экономическим элементам позволяет выделить две основные их группы: затраты прошлого труда, овеществленные в стоимости потребленных предметов труда (сырье, материалы и т.д.) и средств труда (амортизация), и затраты живого труда (расходы на оплату труда с отчислениями на социальные нужды). Из прочих затрат обычно две трети относятся к материальным затратам, а остальное – к затратам живого труда.

По данным отчетов можно определить производственную себестоимость товарной продукции (работ, услуг). Для этого необходимо из общей суммы затрат на производство и реализацию продукции (работ, услуг) исключить затраты на непроизводственные счета, вычесть изменение остатка по счету «Расходы будущих периодов», изменение остатков незавершенного производства, полуфабрикатов, инструментов и приспособлений собственной выработки, не включаемых в стоимость продукции, и добавить прирост или вычесть уменьшение остатка по счету «Резерв предстоящих расходов и платежей». [23, с. 186]

1.2 Динамики производственных затрат на производство зерна, сахарной свеклы, подсолнечника за 6 лет

Произведем анализ динамики производственных затрат зерна, сахарной свеклы и подсолнечника за 6 лет. Исходные данные приведены в таблице 1.1. Для расчета показателей ряда динамики, темпов роста и прироста и других используются следующие выражения:

Абсолютный прирост

Базисный:

Цепной:

Темпы роста:

Базисный:

Цепной:

Темпы прироста:

Базисный:

Цепной:

Средний:

Абсолютное значение 1% прироста:

Таблица 1. Расчет показателей динамики производственных затрат за 6 лет

Год

Производ-

ственные

затраты, тыс. руб.

Абсолютное отклонение, ц

Темп роста, %

Темп прироста, %

Абсолютное значение 1% прироста

цепной

базисный

цепной

базисный

цепной

базисный

2001

308

2002

270

-38

0.88

-0.12

2.7

2003

220

-50

0.81

0.71

-0.19

-0.16

2.2

2004

245

1.11

0.91

0.11

0.08

2.45

2005

361

116

1.47

1.64

0.47

0.38

3.61

2006

477

116

1.32

1.95

0.32

0.38

4.77

Вывод: Динамика производственных затрат характеризуется общим подъемом на 20,3% за исследуемый период. При этом как цепные так и базисные показатели темпов прироста имеют преимущественно положительное значение, что позволяет характеризовать динамику как общее подъем производственных затрат.

1.3 Динамика себестоимости 1 ц. зерна (сахарной свеклы, подсолнечника). Темпы ее роста и прироста, показатели вариации за 9 лет. Выявление тенденций изменения себестоимости1 ц. за 9 лет

Таблица 2. Динамика себестоимости 1 ц. за 9 лет

Год

Себестоимость 1 ц., руб.

Темп роста

Темп прироста

цепные

базисные

цепные

базисные

1998

139.82

1999

240.74

1.72

0.72

2000

193.55

0.80

1.38

-0.20

-0.34

2001

218.13

1.13

1.56

0.13

0.18

2002

212.17

0.97

1.52

-0.03

-0.04

2003

183.33

0.86

1.31

-0.14

-0.21

2004

198.38

1.08

1.42

0.08

0.11

2005

293.5

1.48

2.10

0.48

0.68

2006

389.07

1.33

2.78

0.33

0.68

Определим средние показатели ряда динамики:

а) Средний абсолютный прирост:

б) Средний темп роста:

в) Средний темп прироста:

Себестоимость зерна (сахарной свеклы, подсолнечника) имеет также тенденцию к подъёму, однако не настолько большую как производственные затраты и составляет за исследуемый период лишь 6,8%.

Произведем выравнивание ряда динамики себестоимости зерна (сахарной свеклы, подсолнечника) для более детального выявления тенденции.

Для этого используем метод укрупнения периодов и скользящей средней за 3 года:

Таблица 3. Выравнивание динамического ряда себестоимости 1 ц. продукции за 9 лет

Год

Себестоимость 1 ц., руб.

Укрупнение периодов, руб.

Скользящая средняя, руб.

сумма за трёхлетие

средняя себестоимость 1 ц. за трехлетие

сумма за трёхлетие

средняя себестоимость 1 ц. за трехлетие

1998

139.82

1999

240.74

574.11

191.37

63.79

2000

193.55

652.42

217.47

2001

218.13

623.85

207.95

2002

212.17

613.63

204.5433

204.54

68.18

2003

183.33

593.88

197.96

2004

198.38

675.21

225.07

2005

293.5

880.95

293.65

97.88

2006

389.07

Применение методов укрупнения периодов и скользящей средней позволяют утверждать, что существует постоянная динамика подъема себестоимости по годам.

Выявим тенденцию изменения себестоимости зерна (сахарной свеклы, подсолнечника) с помощью метода аналитического выравнивания.

Выравнивание осуществим по прямой:

Таблица 4 Аналитическое выравнивание себестоимости 1 ц. продукции

Год

Себестоимость 1 ц.

Условное обозначение периода времени t

Расчетные данные

t²

y*t

1998

139.82

-4

-559.3

154.65

1999

240.74

-3

-722.2

173.45

2000

193.55

-2

-387.1

192.25

2001

218.13

-1

-218.1

211.05

2002

212.17

229.85

2003

183.33

248.65

2004

198.38

396.76

267.45

2005

293.5

880.5

286.25

2006

389.07

1556.3

305.05

Итого

2068.7

1130.1

2068.7

Рассчитаем значения коэффициентов уравнения:

Уравнение общей тенденции ряда динамики:

Таким образом, с помощью методов выравнивания выявлена общая тенденция подъема себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период.

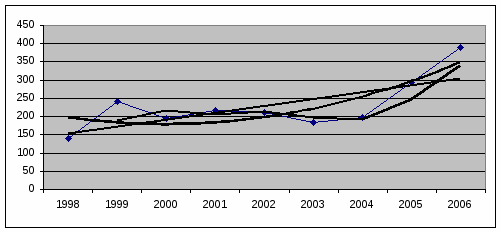
Рисунок 1. Аналитическое выравнивание себестоимости 1 ц. продукции

Вывод:

Динамика себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период носит устойчивую тенденцию к повышению, при этом локальная колебимость признака, имеющая место в 2000, 2003 и 204 годах не оказала существенного влияния на общие результаты выравнивания, а значит, является статистически малозначимой.

2. Индексный метод анализа

2.1 Сущность индекса, их виды

Индексы относятся к важнейшим обобщающим показателям. Слово «индекс» имеет несколько значений: показатель, указатель, опись, реестр. Оно используется как понятие в математике, экономике, метеорологии и других науках [20, с. 183].

В статистике под индексом понимается относительный показатель который выражает соотношение величин какого-либо явления во времени, в пространстве или дает сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.).

В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой «i» обозначаются индивидуальные (частные) индексы, буквой «I» -общие индексы. Знак внизу справа означает период: 0 - базисный; 1 – отчетный /5/.

Используются определенные символы для обозначения индексируемых показателей:

q - количество (объем) произведенной продукции (или количество проданного товара) данного вида в натуральном выражении;
р - цена единицы продукции или товара;
z - себестоимость единицы продукции;
t - затраты рабочего времени (труда) на производство единицы продукт ции данного вида, т.е. трудоемкость единицы изделия;
Т - общие затраты рабочего времени (труда) на производство продукции данного вида или численность работников предприятия, фирмы и т.д.
w=q:T - производство продукции данного вида в единицу времени или в расчёте на одного рабочего, т.е. уровень производительности труда в стоимостном выражении;
v - выработка продукции в натуральном выражении на одного рабочего или в единицу времени;
F = zq - общие затраты на производство продукции данного вида;
Q=pq- общая стоимость произведенной продукции данного вида или товарооборот.

Все экономические индексы можно классифицировать по следующим признакам [1, с. 85]:

степень охвата явления;
база сравнения;
вид весов (соизмерителя);
форма построения;
характер объекта исследования:
объект исследования;
состав явления;
период исчисления.

По степени охвата явления индексы бывают индивидуальные и сводные. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления, например изменения объема производства отдельных видов продукции (телевизоров, электроэнергии и т.д.), а также цен на акции какого-либо предприятия. Для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы (изменения физического объема продукции, включающей разноименные товары, индекса цен акций предприятий региона и т.п.), рассчитывают сводные, или общие, индексы.

Если индексы охватывают не все элементы сложного явления, а только часть их, то такие индексы называются групповыми, или субиндексами, например индексы физического объема продукции по отдельным отраслям промышленности, индексы цен по группам продовольственных и непродовольственных товаров. Групповые индексы отражают закономерности в развитии отдельных частей изучаемых явлений. В таких индексах проявляется их связь с методом группировок. [4, с. 89]

По базе сравнения все индексы можно разделить на две группы: динамические и территориальные. Первая группа индексов отражает изменение явления во времени. Например, индекс цен на продукцию в 2005 г. по сравнению с предыдущим годом; индекс стоимости потребительской корзины в августе по сравнению с июлем 2005 г.

При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий период, который называют базисным. Однако в качестве последнего могут быть использованы и прогнозные, и плановые показатели.

Динамические индексы бывают базисными и цепными.

Вторая группа индексов (территориальные) применяется для межрегиональных сравнений. Большое значение эти индексы имеют в международной статистике при сопоставлении показателей социально-экономического развития различных стран. Например, индекс цен на автомобили в США по сравнению с Японией, индекс стоимости потребительской корзины в Москве по сравнению с Санкт-Петербургом. [7, с. 69]

По виду весов индексы бывают с постоянными и переменными весами.

В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы - производные, они получаются в результате преобразования агрегатных индексов.

По характеру объекта исследования общие индексы подразделяются на индексы количественных (объемных) и качественных показателей. В основе такого деления индексов лежит вид индексируемой величины. К первой группе индексов относятся, например, индексы объема продаж долларов США на Московской межбанковской валютной бирже, а ко второй - индекс курса немецкой марки.

По объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д.

По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. Деление индексов на эти две группы используется для анализа динамики средних показателей.

По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные. [13, с. 191]

С помощью экономических индексов решаются следующие задачи [16, с. 281]:

измерение динамики социально-экономического явления за два и более периодов времени;
измерение динамики среднего экономического показателя;
измерение соотношения показателей по разным регионам;
определение степени влияния изменений значений одних показателей на динамику других;
пересчет значения макроэкономических показателей из фактических цен в сопоставимые.

Каждая из этих задач решается с помощью различных индексов.

Индивидуальные индексы получают в результате сравнения однотоварных явлений /10/. Например, индекс цен на растительное масло определяется как отношение цены на этот товар в текущем периоде к цене базисного периода.

Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения, и их расчет не требует знания специальных правил.

В зависимости от экономического назначения индивидуальные индексы бывают физического объема продукции, себестоимости, цен, трудоемкости и т.д.

Индекс физического объема продукции i рассчитывается по формуле:

, (1)

где q₁ - количество (объем) произведенной продукции (или количество проданного товара) данного вида в натуральном выражении за отчетный период;

q₀ - количество (объем) произведенной продукции (или количество проданного товара) данного вида в натуральном выражении за базовый период

Этот индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) выпуска товара. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная величина покажет, на сколько процентов возрос (уменьшился) выпуск продукции. В знаменателе может быть не только количество продукции, произведенной за какой-то предыдущий период, но и плановое значение (q_пл), нормативное (q_н) или эталонное значение, принятое за базу сравнения (q_э). Тогда формула (1) примет соответственно следующий вид:

(2)

(3)

(4)

Индексы других показателей строятся аналогично. Индивидуальный индекс цен:

, (5)

где р₁ - цена единицы продукции или товара за отчетный период;

р₀ - цена единицы продукции или товара за базовый период.

характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным. [21, с. 290]

Индивидуальный индекс себестоимости единицы продукции:

, (6)

где z₁ - себестоимость единицы продукции за отчетный период;

z₀ - себестоимость единицы продукции за базовый период.

Он показывает изменение себестоимости единицы продукции в текущем периоде по сравнению с базисным.

Производительность труда может быть измерена количеством продукции, производимой в единицу времени (v), или затратами рабочего времени на производство единицы продукции (t). Поэтому можно построить:

• индекс количества продукции, произведенной в единицу времени:

(7)

• индекс производительности труда по трудовым затратам:

(8)

Так как между количеством продукции, произведенной в единицу времени, и затратами рабочего времени на производство единицы продукции существует обратно пропорциональная зависимость, т.е.:

(9)

то индекс (8) получится в результате деления величины показателя в базисном периоде на величину в текущем периоде.

Для характеристики производительности труда часто используется индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего:

(10)

где р - сопоставимые цены.

Индивидуальные индексы (7 и 10) показывают, во сколько раз производительность труда в базисном периоде выше (ниже), чем в отчетном.

Индекс, исчисленный по формуле (8), показывает, во сколько раз производительность труда в базисном периоде выше (ниже), чем в отчетном.

Индивидуальный индекс стоимости продукции отражает, во сколько раз изменилась стоимость какого-либо товара в текущем периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости товара, и определяется по формуле:

(11)

Индивидуальный индекс численности рабочих можно рассчитать следующим образом:

(12)

Он показывает, во сколько раз изменилась численность рабочих в текущем периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) численности рабочих.

В экономических расчетах чаще всего используются общие индексы, которые характеризуют изменение совокупности в целом. Построение этих индексов и является содержанием индексной методологии. В индексной теории сложились две концепции: синтетическая и аналитическая. Они по-разному интерпретируют общие индексы [24, с. 87].

Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных (разнотоварных) явлений, отдельные части или элементы которых непосредственно несоизмеримы, и поэтому индексы - показатели синтетические. Например, промышленные предприятия производят несколько видов продукции, имеющей различное назначение. Следовательно, путем суммирования количества произведенных товаров различных видов нельзя получить показатель физического объема продукции. Методология построения общих индексов предусматривает, прежде всего, приведение разнотоварных явлений к соизмеримому виду.

В аналитической теории индексы трактуются как показатели, необходимые для измерения влияния изменения составных частей, компонентов, факторов сложного явления на изменение уровня этого явления. Например, изменение общей величины товарооборота в текущем периоде по сравнению с базисным связано с изменением как физического объема продаж товаров, так и цен по каждому виду товаров. Поэтому индексная методология предусматривает определение влияния каждого из факторов путем элиминирования влияния других факторов на уровень изучаемого явления.

Таким образом, общие индексы являются синтетическими и аналитическими показателями. [2, с. 36]

Общие индексы строят для количественных (объемных) и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или средневзвешенную.

Агрегатный индекс — сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов /10/.

Агрегат (лат. aggregates) означает складываемый, суммируемый. Особенность этой формы индекса состоит в том, что в агрегатной форме непосредственно сравниваются две суммы одноименных показателей. В настоящее время это наиболее распространенная форма индексов, используемая в практической статистике многих стран мира.

Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса).

Индексируемой величиной называется признак, изменение которого изучается (цена товаров, курс акций, затраты рабочего времени на производство продукции, количество проданных товаров и т.д.). Вес индекса - это величина, служащая для целей соизмерения индексируемых величин.

За каждым экономическим индексом стоят определенные экономические категории. Экономическое содержание индекса предопределяет методику его расчета. [3, с. 286]

Методика построения агрегатного индекса предусматривает ответ на три вопроса:

какая величина будет индексируемой;
по какому составу разнородных элементов явления необходимо исчислить индекс;
что будет служить весом при расчете индекса.

При выборе веса индекса принято руководствоваться следующим правилом /5/: если строится индекс количественного показателя, то веса берутся за базисный период; при построении индекса качественного показателя используются веса отчетного периода.

Построим три индекса - стоимости продукции, физического объема продукции и цен.

Стоимость продукции - это произведение количества продукции в натуральном выражении (q) на ее цену (р).

Индекс стоимости продукции, или товарооборота (), представляет собой отношение стоимости продукции текущего периода () к стоимости продукции в базисном периоде () и определяется по формуле:

(13)

Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Если из значения индекса стоимости (13) вычесть 100% (Ipq - 100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Разность числителя и знаменателя () показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Аналогично строятся индексы для показателей, которые являются произведением двух сомножителей: издержек производства (произведение себестоимости единицы продукции на количество продукции); затрат времени на производство всей продукции (произведение затрат времени на производство единицы продукции на количество выработанной продукции).

Индекс физического объема продукции - это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом - цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема - индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:

(14)

где в числителе дроби - условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе - фактическая стоимость товаров, произведенных в базисном периоде. Если объектом исследования является отдельное предприятие, то индекс определяется по совокупности произведенных товаров; когда объект исследования - отрасль промышленности, индекс рассчитывается по совокупности всех товаров, произведенных в отрасли, или отдельным их группам в зависимости от цели анализа. Если же объектом исследования является какой-либо регион, то индекс рассчитывается по товарам, произведенным предприятиями региона. [10, с. 350]

Индекс физического объема продукции (14) показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства. Если из значения индекса физического объема продукции (14) вычесть 100% (I_q - 100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за роста (снижения) объема ее производства. Разность числителя и знаменателя () показывает, на сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема. Изменение цен на продукцию в текущем периоде по сравнению с базисным не влияет на величину индекса.

Индекс цен - это индекс качественного показателя. Индексируемой величиной будет цена товара, так как этот индекс характеризует изменение цен. Весом будет выступать количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую можно суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами.

Индекс цен определяется по следующей формуле:

(15)

где в числителе дроби - фактическая стоимость продукции текущего периода, а в знаменателе - условная стоимость тех же товаров в ценах базисного периода.

Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен. Если из значения индекса (15) вычесть 100% (Iр - 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции из-за изменения цен, а разность числителя и знаменателя () - на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен. Изменение количества произведенной продукции в текущем периоде по сравнению с базисным не влияет на величину индекса.

Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связь существует и между индексами стоимости, физического объема и цен, т.е.:

(16)

Или

(17)

Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора. Алгебраическая сумма этих разностей равна разности числителя и знаменателя индекса стоимости продукции:

(18)

Равенства (16-18) выполняются в том случае, если при исчислении индекса объемного показателя веса были зафиксированы на уровне базисного периода, а при расчете индекса качественного показателя - на уровне отчетного периода.

Помимо агрегатных индексов в статистике применяется другая их форма - средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, однако возможно исчислить его как средний из индивидуальных. Точно так же, если не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного периода, то можно определить общий индекс физического объема продукции как средневзвешенную величину

Средний индекс- это индекс, вычисленный как средняя величина из индивидуальных индексов. Агрегатный индекс является основной формой общего индекса, поэтому средний индекс должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.

Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса рассчитанного по формуле средней арифметической, будет равна агрегатному индексу. [17,с. 156]

Средний арифметический индекс физического объема продукции исчисляется по формуле:

(19)

Так как i_q= q₁ / q₀, то формула этого индекса легко преобразуется в формулу 14). Весами в формуле (19) является стоимость продукции базисного периода.

Средний арифметический индекс производительности труда определяется следующим образом:

(20)

Так как i_t = t₀ / t₁ то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции в текущем периоде.

В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмипина и определяется следующим образом:

(21)

Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда, или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности.

Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. При анализе качественных показателей данная форма индекса применяется для исчисления приведенных выше индексов (формулы (20)-(21)).

Индексы других качественных показателей (цен, себестоимости и т.д.) определяются по формуле средней гармонической взвешенной величины.

Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.

Например, индекс себестоимости можно исчислить так:

(22)

а индекс цен:

(23)

Таким образом, при определении среднего гармонического индекса себестоимости весами являются издержки производства текущего периода, а при вычислении индекса цен веса - стоимость продукции этого периода.

Средние индексы широко используются для анализа рынка ценных бумаг. Наиболее известными являются индексы Доу-Джонса, Стэн-дарда и Пура.

Индекс Доу-Джонса (Dow Jones Industrial Average Index) определится как средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется их значение на момент закрытия биржи. Групповые индексы определяются по ценам акций 30 промышленных, 20 транспортных и 15 компаний сферы услуг. Общий индекс рассчитывается по всем 65 компаниям. Их перечень был составлен в 1928 г. В качестве базисного выбран 1920 г. Первоначальная методика исчисления индекса была разработана основателем и редактором крупнейшей в США газеты «Уолл-стрит джорнел» Чарлзом Доу. [22, с. 490]

Индекс Стэндарда и Пура (Standard and Poor's 500 Stock Index) -индекс, рассчитываемый по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи как средний взвешенный показатель, учитывающий общее число выпущенных компанией акций. В число компаний, акции которых включены в индекс, входят 400 промышненных корпораций, 40 - финансовых, 20 - транспортных и 40 - сферы услуг.

При изучении динамики качественных показателей приходится определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов—изменением значения индексируемого показателя у отдельных групп единиц и изменением структуры явления /10/. Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности. Так, средняя заработная плата на предприятии может вырасти в результате роста оплаты труда работников или увеличения доли высокооплачиваемых сотрудников. Снижение трудоемкости производства единицы продукции по совокупности предприятий отрасли может быть обусловлено повышением производительности труда на предприятиях или концентрацией производства продукции на заводах с низкой трудоемкостью. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определить степень влияния каждого из факторов на общую динамику средней. [14, с. 133]

Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:

(24)

где I_пс - индекс переменного состава.

Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов).

Индекс постоянного (фиксированного) состава - это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины.

Индекс фиксированного состава определяется как агрегатный индекс. Так, индекс фиксированного состава себестоимости продукции рассчитывают по формуле:

(25)

где I_фс - индекс фиксированного состава.

Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):

(26)

где I_cc - индекс структурных сдвигов.

Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:

(27)

2.2 Индексный анализ изменения средней себестоимости производственных затрат

Исходные данные для индексного анализа по хозяйствам приведены в таблице 5.

Таблица 5. Исходные данные для индексного анализа

Наимено-вание предприятий

Себестоимость 1 ц. продукции

Количество произведенной продукции, ц.

Производственные затраты, тыс. руб.

Базисный год (z₀)

Отчетный год (z₁)

Базисный год (q₀)

Отчетный год (q₁)

Базисный год (z_0q0)

Отчетный год (z_1q1)

Условный (z_0q1)

100.16

103.96

33507

28810

3356061.1

2995088

2885610

144.67

187.91

32535

17987

4706838.5

3379937

2602179

132.66

119.92

21302

19113

2825923.3

2292031

2535531

86.4

99.73

33183

30312

2867011.2

3023016

2618957

84.06

153.63

40790

41028

3428807.4

6303132

3448814

63.3

120.36

28640

24809

1812912

2986011

1570410

39.58

54.63

30244

29929

1197057.5

1635021

1184590

215.73

179.97

26918

23759

5807020.1

4275907

5125529

162.7

258.3

38014

50990

6184877.8

13170717

8296073

52.3

152.09

60322

36425

3154840.6

5539878

1905028

58.07

119.64

236.42

12019

13728.909

1437953

697943.3

67.6

76.24

19070

21053

1289132

1605081

1423183

87.75

110.83

21972

13678

1928043

1515933

1200245

140.58

156.47

60114

72990

8450826.1

11420745

10260934

81.8

163.11

42775

36465

3498995

5947806

2982837

160.89

165.22

26540

33677

4270020.6

5564114

5418293

123.13

193.39

32591

30534

4012929.8

5904970

3759651

103.06

184.72

22512

23609

2320086.7

4361054

2433144

149.06

193

9620

10689

1433957.2

2062977

1593302

148.36

148.38

22243

22240

3299971.5

3299971

3299526

97.3

163.82

10986

19845

1068937.8

3251008

1930919

Итого

108.98

153.29

614114

599961

66927978

91972351

67172696

Проведем индексный анализ средней себестоимости 1 ц. зерна (сахарной свеклы, подсолнечника) по факторам:

Определим среднюю базисную, условную и отчетную себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника):

Найдем общее изменение средней себестоимости 1 ц. зерна (сахарной свеклы, подсолнечника) в отчетном году по отношению к базисному году:

а) в относительном выражении:

или 140 %

б) в абсолютном выражении:

ц/га

Таким образом, средняя себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника) в отчетном году по сравнению с базисным увеличилась на 44,31 или на 40 %.

Определим влияние факторов на среднюю себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника):

Влияние урожайности:

а) в относительном выражении:

или 137 %

б) в абсолютном выражении:

За счет увеличения урожайности 1 ц. зерна (сахарной свеклы, подсолнечника) средняя себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника) увеличилась на 41,33 ц/га или на 37 %

Влияние структуры:

а) в относительном выражении:

или 102 %

б) в абсолютном выражении:

За счет повышения урожайности средняя себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника) увеличилась на 2,98 ц/га или на 1,02 %

Относительная взаимосвязь средней себестоимости по факторам:

1,39 = 1,37*1,02

Абсолютная взаимосвязь абсолютной урожайности по факторам:

Проведем индексный анализ производственных затрат:

а) в относительном выражении:

или 137 %

б) в абсолютном выражении:

ц.

Таким образом, производственные затраты в отчетном году по сравнению с базисным увеличились на 25044373 ц. или на 37 %.

Определим влияние факторов на производственные затраты:

1) Влияние себестоимости 1 ц. продукции, произведенной в отдельных хозяйствах:

а) в относительном выражении:

или 137 %

б) в абсолютном выражении:

За счет увеличения себестоимости 1 ц. продукции в отдельных хозяйствах производственные затраты увеличились на ц или на 37 %

2) Влияние структуры произведенной продукции:

а) в относительном выражении:

или 102 %

б) в абсолютном выражении:

ц.

За счет улучшения структуры произведенной продукции производственные затраты увеличилась на ц или на 2 %

3) Влияние количества произведенной продукции:

а) в относительном выражении:

или на 97 %

б) в абсолютном выражении:

За счет уменьшения количества произведенной продукции производственные затраты уменьшились на 1542393,94 ц. или на 3 %

Относительная взаимосвязь по факторам:

1,35 = 1,37 * 1,02 * 0,97

Абсолютная взаимосвязь абсолютной себестоимости по факторам:

Таким образом, повышение средней себестоимости произошло за счет повышения урожайности на 41,33 ц/га или на 37 %, а за счет фактора улучшения структуры произведенной продукции средняя себестоимость увеличилась на 1799883 ц/га или на 2 %.

На объем производственных затрат положительно повлияли повышение себестоимости в отдельных хозяйствах и отрицательно - уменьшение количества произведенной продукции, положительно повлияло улучшение структуры произведенной продукции. В результате производственные затраты в отчетном году по сравнению с базисным увеличились на 25044373 ц. или на 37 %.

3.Выявление взаимосвязи методом аналитической группировки

3.1 Сущность группировки, их виды и значение

Группировка — это распределение единиц по группам в соответствии со следующим принципом: различия между единицами, отнесенными к одной группе, должны быть меньше, чем между единицами, отнесенными к разным группам.

Группировка лежит в основе всей дальнейшей работы с собранной информацией. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, анализа причин различий между группами, изучения взаимосвязей между признаками. Если рассчитать сводные показатели только в целом по совокупности, то мы не сможем уловить ее структуры, роли отдельных групп, их специфики.

Однородность (гомогенность) данных является исходным условием их статистического описания и анализа - вычисления и интерпретации обобщающих показателей, построения уравнения регрессии, измерения корреляции, статистического умозаключения. [8, с. 90]

Таким образом, значение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в компактном, обозримом виде. Кроме того, группировка создает основу для последующей сводки и анализа данных.

Для изучения структурных изменений в экономике государственная статистика использует группировку хозяйственных субъектов по формам собственности и организационно-правовым формам.

Сводные показатели для отдельных групп являются типичными и устойчивыми, если, во-первых, группировка проведена правильно, во-вторых, группы имеют достаточную численность. Первое условие связано с тем, что деление на группы далеко не всегда очевидно. Выполнение второго условия необходимо, так как при достаточно большом числе единиц (не менее 5 единиц в группе) в сводных показателях взаимопогашаются случайные характеристики и проявляются закономерные, типичные.

Для решения задачи группировки нужно установить правила отнесения каждой единицы к той или иной группе.

В эти правила входят определения тех характеристик (признаков), по которым будет проводиться группировка (так называемых группировочных признаков), и их значений, отделяющих одну группу от другой (интервалов группировки).

Группировка называется простой (монотетической), если для ее построения используется один группировочный признак. Если группировка проводится по нескольким признакам, она называется сложной (политетической). Обычно такая группировка проводится как комбинационная, т.е. группы, выделенные по одному признаку, подразделяются на подгруппы по другому признаку. Казалось бы, этот метод выделения групп должен быть лучше простой группировки - ведь трудно ожидать, что различия между группами можно уловить лишь на основе одного признака. Однако комбинация признаков приводит к дроблению совокупности в геометрической прогрессии: число групп будет равно произведению числа группировочных признаков (l) на число выделенных категорий по каждому из них (т): к = l * т. Данные становятся труднообозримыми, группы включают малое число единиц, групповые показатели становятся ненадежными.

Альтернативой является проведение многомерных группировок или многомерных классификаций

Очевидно, что метод группировок тесно связан с представлением данных в виде групповых или комбинационных таблиц, а также с графическим представлением структуры совокупности ее частей и соотношений между ними.

Группировка производится с целью установления статистических связей и закономерностей, построения описания объекта, выявления структуры изучаемой совокупности. Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок: типологические, структурные, аналитические.

Типологическая группировка служит для выделения социально-экономических типов. Этот вид группировок в значительной степени определяется представлениями экспертов о том, какие типы могут встретиться в изучаемой совокупности. Чтобы пояснить особенность этой группировки, остановимся на последовательности действий для ее проведения:

1) называются те типы явлений, которые могут быть выделены;

2) выбираются группировочные признаки, формирующие описание типов;

3) устанавливаются границы интервалов;

4) группировка оформляется в таблицу, выделенные группы (на основе комбинации группировочных признаков) объединяются в намеченные типы, и определяется численность каждого из них.

Структурная группировка характеризует структуру совокупности по какому-либо одному признаку.

Аналитическая группировка характеризует взаимосвязь между двумя и более признаками, из которых один рассматривается как результат, другой (другие) — как фактор (факторы).

3.2 Аналитическая группировка хозяйств по одному из факторов (Х- урожайность зерна (сахарной свеклы, подсолнечника), уровень интенсификации), влияющих на себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника)

Проведем группировку предприятий, образовав 5 групп:

Рассчитаем величину интервала:

Таблица 6. Исходные данные по группам

Группа предприятий по урожайности ц/га (Х)

Номер предприятия

Валовой сбор, ц.

Площадь посева, га

Себестоимость произведенной продукции

Уровень интенсификации, тыс. руб.

Число предприятий, ед.

Границы групп

13.2 - 18.1

21049.8

1594

1604151

1007

12027.4

781

1438958

1841

10696.6

677

2064444

3047

19057

1121

2285315

2045

36523.8

2064

6035949

2882

28729.2

1614

298688

1856

Итого по 1 группе

128083.8

7851

13727505

12678

18.1 - 23

30258.9

1601

3017720

1888

30511.8

1541

5636140

3832

19820.4

996

3246978

3264

33640

1682

6505640

3308

29936.4

1482

1635426

1103

23649.5

1165

4564354

3743

24840

1200

2989742

2488

36485.5

1697

5549080

3264

40918.6

1877

6286325

358

Итого по 2 группе

270061.1

13241

39431405

23248

23 - 27.9

18008.2

677

3383921

4993

30690

1100

4969325

4526

Итого по 3 группе

48698.2

1777

8353246

9519

27. 9 - 32.8

22226.4

756

3297953

4365

126387

4185

30067467

7184

23759.5

779

4275997

5489

Итого по 4 группе

172372.9

5720

37641417

17038

32.8 - 37.7

50970.4

1352

13165654

9742

Итого по 5 группе

50970.4

1352

13165654

9742

Итого

670186.4

29941

112319227

72225

Таблица 7. Аналитическая группировка сельскохозяйственных предприятий по урожайности

Группа предприятий по урожайности ц/га (Х)

Количество предприятий, ед.

Себестоимость 1 ц., руб.

Урожайность, ц/га

Уровень интенсификации, тыс. руб.

Границы групп

13.2 - 18.1

107175.96

16.31

2113

18.1 - 23

146009.19

20.39

2583.11

23 - 27.9

171530.89

27.4

4759.5

27. 9 - 32.8

218372.01

30.13

5679.33

32.8 - 37.7

258299.99

37.7

9742

В среднем по совокупности предприятий

180277.608

26.386

4975.388

Таким образом, между урожайностью и себестоимостью 1 ц. зерна (сахарной свеклы, подсолнечника) существует прямая связь, т. е. повышение урожайности на 25 % даёт повышение себестоимости на 38833,23 руб.

4.Корреляционно-регрессионный анализ

4.1 Сущность и основные условия применения корреляционного анализа

В соответствии с сущностью корреляционной связи ее изучение имеет две цели:

1) измерение параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной (зависимость средних величин результативного признака от значений одного или нескольких факторных признаков);

2) измерение тесноты связи двух (или большего числа) признаков между собой.

Вторая задача специфична для статистических связей, а первая разработана для функциональных связей и является общей. Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К. Ф. Гауссом (1777-1855). Он состоит в минимизации суммы квадратов отклонений фактически измеренных значений зависимой переменной у от ее значений, вычисленных по уравнению связи с факторным признаком (многими признаками) х. [5, с. 78]

Для измерения тесноты связи применяется несколько показателей. При парной связи теснота связи измеряется прежде всего корреляционным отношением, которое обозначается греческой буквой η. Квадрат корреляционного отношения - это отношение межгрупповой дисперсии результативного признака, которая выражает влияние различий группировочного факторного признака на среднюю величину результативного признака, к общей дисперсии результативного признака, выражающей влияние на него всех причин и условий. Квадрат корреляционного отношения называется коэффициентом детерминации:

(28)

где k - число групп по факторному признаку;

N — число единиц совокупности;

у_i — индивидуальные значения результативного признака;

_i - его средние групповые значения;

- его общее среднее значение;

f_i - частота в j-й группе.

Формула (1) применяется при расчете показателя тесноты связи по аналитической группировке. При вычислении корреляционного отношения по уравнению связи (уравнению парной или множественной регрессии) применяется формула (2):

(29)

где - индивидуальные значения у по уравнению связи.

Сумма квадратов в числителе - это объясненная связью с фактором х (факторами) дисперсия результативного признака у. Она вычисляется по индивидуальным данным, полученным для каждой единицы совокупности на основе уравнения регрессии. [11, с. 300]

Если уравнение выбрано неверно или сделана ошибка при расчете его параметров, то сумма квадратов в числителе может оказаться большей, чем в знаменателе, и отношение утратит тот смысл, который оно должно иметь, а именно какова доля общей вариации результативного признака, объясняемая на основе выбранного уравнения связи его с факторным признаком (признаками). Чтобы избежать ошибочного результата, лучше вычислять корреляционное отношение по другой формуле (3), не столь наглядно выявляющей сущность показателя, но зато полностью гарантирующей от возможного искажения:

(30)

В числителе формулы (3) стоит сумма квадратов отклонений фактических значений признака у от его индивидуальных расчетных значений, т.е. доля вариации этого признака, не объясняемая за счет входящих в уравнение связи признаков-факторов. Эта сумма не может стать равной нулю, если связь не является функциональной. При неверной формуле уравнения связи или ошибке в расчетах возрастают расхождения фактических и расчетных значений, и корреляционное отношение снижается, как логически и должно быть.

В основе перехода от формулы (2) к формуле (3) лежит известное правило разложения сумм квадратов отклонений при группировке совокупности:

D_общ=D_межгр+D_{внутригр}

Согласно этому правилу можно вместо межгрупповой (факторной) дисперсии использовать разность:

D_общ - D_{внутригр}

что дает:

(31)

При расчете η не по группировке, а по уравнению корреляционной связи (уравнению регрессии) мы используем формулу (3). В этом случае правило разложения суммы квадратов отклонений результативного признака записывается как

D_общ=D_объясн _уравн _регр+D_ост

Важнейшее положение, которое следует теперь усвоить любому, желающему правильно применять метод корреляционно-регрессионного анализа, состоит в интерпретации формул (2) и (3). Это положение гласит:

Уравнение корреляционной связи измеряет зависимость между вариацией результативного признака и вариацией факторного признака (признаков). Меры тесноты связи измеряют долю вариации результативного признака.

Интерпретировать корреляционные показатели строго следует лишь в терминах вариации (различий в пространстве) отклонений от средней величины. Если же задача исследования состоит в измерении связи не между вариацией двух признаков в совокупности, а между изменениями признаков объекта во времени, то метод корреляционно-регрессионного анализа требует значительного изменения. [15, с. 145]

Из вышеприведенного положения об интерпретации показателей корреляции следует, что нельзя трактовать корреляцию признаков как связь их уровней. Это ясно хотя бы из следующего примера. Если бы все крестьяне области внесли под картофель одинаковую дозу удобрений, то вариация этой дозы была бы равна нулю, а следовательно, она абсолютно не могла бы влиять на вариацию урожайности картофеля. Параметры корреляции дозы удобрений с урожайностью будут тогда строго равны нулю. Но ведь и в этом случае уровень урожайности зависел бы от дозы удобрений - он был бы выше, чем без удобрений.

Итак, строго говоря, метод корреляционно-регрессионного анализа не может объяснить роли факторных признаков в создании результативного признака. Это очень серьезное ограничение метода, о котором не следует забывать.

Следующий общий вопрос - это вопрос о «чистоте» измерения влияния каждого отдельного факторного признака. Группировка совокупности по одному факторному признаку может отразить влияние именно данного фактора на результативный признак при условии, что все другие факторы не связаны с изучаемым, а случайные отклонения и ошибки взаимопогасились в большой совокупности. Если же изучаемый фактор связан с другими факторами, влияющими на результативный признак, будет получена не «чистая» характеристика влияния только одного фактора, а сложный комплекс, состоящий как из непосредственного влияния фактора, так и из его косвенных влияний, через его связь с другими факторами и их влияние на результативный признак. Данное положение полностью относится и к парной корреляционной связи.

Однако коренное отличие метода корреляционно-регрессионного анализа от аналитической группировки состоит в том, что корреляционно-регрессионный анализ позволяет разделить влияние комплекса факторных признаков, анализировать различные стороны сложной системы взаимосвязей. Если метод комбинированной аналитической группировки, как правило, не дает возможность анализировать более 3 факторов, то корреляционный метод при объеме совокупности около ста единиц позволяет вести анализ системы с 8-10 факторами и разделить их влияние.

Наконец, развивающиеся на базе корреляционно-регрессионного анализа многомерные методы (метод главных компонент, факторный анализ) позволяют синтезировать влияние признаков (первичных факторов), выделяя из них непосредственно не учитываемые глубинные факторы (компоненты). Например, изучая корреляцию ряда признаков интенсификации сельскохозяйственного производства, таких, как фондообеспеченность, затраты труда на единицу Площади, энергообеспеченность, внесение удобрений на единицу площади, плотность поголовья скота, можно синтезировать общую часть их влияния на уровень продукции с единицы площади или на производительность труда, получив обобщенный фактор «интенсификация производства», непосредственно не измеримый, не отражаемый единым показателем.

Правильное применение и интерпретация результатов корреляционно-регрессионного анализа возможны лишь при понимании всех специфических черт, достоинств и ограничений метода.

Необходимо сказать и о других задачах применения корреляционно-регрессионного метода, имеющих не формально математический, а содержательный характер.

1. Задача выделения важнейших факторов, влияющих на результативный признак (т.е. на вариацию его значений в совокупности). Эта задача решается в основном на базе мер тесноты связи факторов с результативным признаком.

2. Задача оценки хозяйственной деятельности по эффективности использования имеющихся факторов производства. Эта задача решается путем расчета для каждой единицы совокупности тех величин результативного признака, которые были бы получены при средней по совокупности эффективности использования факторов и сравнения их с фактическими результатами производства,

3. Задача прогнозирования возможных значений результативного признака при задаваемых значениях факторных признаков.

Такая задача решается путем подстановки ожидаемых, или планируемых, или возможных значений факторных признаков в уравнение связи и вычисления ожидаемых значений результативного признака.

Приходится решать и обратную задачу: вычисление необходимых значений факторных признаков для обеспечения планового или желаемого значения результативного признака в среднем по совокупности. Эта задача обычно не имеет единственного решения в рамках данного метода и должна дополняться постановкой и решением оптимизационной задачи на нахождение наилучшего из возможных вариантов ее решения (например, варианта, позволяющего достичь требуемого результата с минимальными затратами).

4. Задача подготовки данных, необходимых в качестве исходных для решения оптимизационных задач. Например, для нахождения оптимальной структуры производства в районе на перспективу исходная информация должна включать показатели производительности на предприятиях разных отраслей и форм собственности. В свою очередь, эти показатели могут быть получены на основе корреляционно-регрессионной модели либо на основании тренда динамического ряда (а тренд - это тоже уравнение регрессии).

При решении каждой из названных задач нужно учитывать особенности и ограничения корреляционно-регрессионного метода. Всякий раз необходимо специально обосновать возможность причинной интерпретации уравнения как объясняющего связь между вариацией фактора и результата. Трудно обеспечить раздельную оценку влияния каждого из факторов. В этом отношении корреляционные методы глубоко противоречивы. С одной стороны, их идеал - измерение чистого влияния каждого фактора. С другой стороны, такое измерение возможно при отсутствии связи между факторами и случайной вариации признаков. А тогда связь является функциональной, и корреляционные методы анализа излишни. В реальных системах связь всегда имеет статистический характер, и тогда идеал методов корреляции становится недостижимым. Но это не значит, что эти методы не нужны.

Данное противоречие означает попросту недостижимость абсолютной истины в познании реальных связей. Приближенный характер любых результатов корреляционно-регрессионного анализа не является поводом для отрицания их полезности. Всякая научная истина — относительна. Забыть об этом и абсолютизировать параметры регрессионных уравнений, меры корреляции было бы ошибкой, так же как и отказаться от использования этих мер.

Поскольку корреляционная связь является статистической, первым условием возможности ее изучения является общее условие всякого статистического исследования: наличие данных по достаточно большой совокупности явлений. По отдельным явлениям можно получить совершенно превратное представление о связи признаков, ибо в каждом отдельном явлении значения признаков кроме закономерной составляющей имеют случайное отклонение (вариацию). Например, сравнивая два хозяйства, одно из которых имеет лучшее качество почв, по уровню урожайности, можно обнаружить, что урожайность выше в хозяйстве с худшими почвами. Ведь урожайность зависит от сотен факторов и при том же самом качестве почв может быть и выше, и ниже. Но если сравнивать большое число хозяйств с лучшими почвами и большое число - с худшими, то средняя урожайность в первой группе окажется выше и станет возможным измерить достаточно точно параметры корреляционной связи.

Какое именно число явлений достаточно для анализа корреляционной и вообще статистической связи, зависит от цели анализа, требуемой точности и надежности параметров связи, от числа факторов, корреляция с которыми изучается. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше - не менее чем в 10 раз больше числа факторов. Еще лучше, если число наблюдений в несколько десятков или в сотни раз больше числа факторов, тогда закон больших чисел, действуя в полную силу, обеспечивает эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков.

Вторым условием закономерного проявления корреляционной связи служит условие, обеспечивающее надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточная качественная однородность совокупности. Нарушение этого условия может извратить параметры корреляции. Например, в массе зерновых хозяйств уровень продукции с гектара растет по мере концентрации площадей, т.е. он выше в крупных хозяйствах. В массе овощных и овоще-молочных хозяйств (пригородный тип) наблюдается та же прямая связь уровня продукции с размером хозяйства. Но если соединить в общую неоднородную совокупность те и другие хозяйства, то связь уровня продукции с размером площади пашни (или посевной площади) получится обратной. Причина в том, что овощные и овоще-молочные хозяйства, имея меньшую площадь, чем зерновые, производят больше продукции с гектара ввиду большей интенсивности производства в данных отраслях, чем в производстве зерна.

Иногда как условие корреляционного анализа выдвигают необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. Это условие связано с применением метода наименьших квадратов при расчете параметров корреляции: только при нормальном распределении метод наименьших квадратов дает оценку параметров, отвечающую принципам максимального правдоподобия. На практике эта предпосылка чаще всего выполняется приближенно, но и тогда метод наименьших квадратов дает неплохие результаты.

Однако при значительном отклонении распределений признаков от нормального закона нельзя оценивать надежность выборочного коэффициента корреляции, используя параметры нормального распределения вероятностей или распределения Стьюдента.

Еще одним спорным вопросом является допустимость применения корреляционного анализа к функционально связанным признакам. Можно ли, например, построить уравнение корреляционной зависимости размеров выручки от продажи картофеля, от объема продажи и цены? Ведь произведение объема продажи и цены равно выручке в каждом отдельном случае. Как правило, к таким жестко Детерминированным связям применяют только индексный метод анализа. Однако на этот вопрос можно взглянуть и с другой точки зрения. При индексном анализе выручки предполагается, что количество проданного картофеля и его цена независимы друг от друга, потому-то и допустима абстракция от изменения одного фактора при измерении влияния другого, как это принято в индексном методе. В реальности количество и цена не являются вполне независимыми друг от друга.

Корреляционно-регрессионный анализ учитывает межфакторные связи, следовательно, дает нам более полное измерение роли каждого фактора: прямое, непосредственное его влияние на результативный признак; косвенное влияние фактора через его влияние на другие факторы; влияние всех факторов на результативный признак. Если связь между факторами несущественна, индексным анализом можно ограничиться. В противном случае его полезно дополнить корреляционно-регрессионным измерением влияния факторов, даже если они функционально связаны с результативным признаком.

4.2 Построение однофакторной корреляционной модели зависимости себестоимости 1 ц. от фактора (Х- урожайность зерна, (сахарной свеклы, подсолнечника), Х – производственных затрат)

В качестве предмета исследования в этом разделе выберем зависимость себестоимости 1 ц. от фактора (Х- урожайность зерна, (сахарной свеклы, подсолнечника), Х – производственных затрат).

Таблица 8. Исходные и расчетные данные построения корреляционно – регрессионной модели себестоимости

Номер предпиятия

Себестоимость 1 ц. продукции, руб.

Факторный признак

х²

ух

у²

у_х

119.64

15.4

237.16

1842.46

14313.73

-38.25

161.92

27.9

778.41

4517.57

26218.09

-103.25

237.9

30.2

912.04

7184.58

56596.41

-115.21

163.82

19.9

396.01

3260.02

26836.99

-61.65

148.38

29.4

864.36

4362.37

22016.62

-111.05

193

15.8

249.64

3049.40

37249.00

-40.33

193

20.3

412.09

3917.90

37249.00

-63.73

184.72

19.8

392.04

3657.46

34121.48

-61.13

193.39

400

3867.80

37399.69

-62.17

165.22

17.7

313.29

2924.39

27297.65

-50.21

152.09

21.5

462.25

3269.94

23131.37

-69.97

258.3

37.7

1421.29

9737.91

66718.89

-154.21

179.97

30.5

930.25

5489.09

32389.20

-116.77

54.63

20.2

408.04

1103.53

2984.44

-63.21

120.36

20.7

428.49

2491.45

14486.53

-65.81

153.63

21.8

475.24

3349.13

23602.18

-71.53

99.73

18.9

357.21

1884.90

9946.07

-56.45

119.92

289

2038.64

14380.81

-46.57

187.91

26.6

707.56

4998.41

35310.17

-96.49

103.96

17.8

316.84

1850.49

10807.68

-50.73

76.24

13.2

174.24

1006.37

5812.54

-26.81

Итого

3267.73

462.3

10925.45

75803.79

558868.53

-1525.53

Определим параметры уравнения регрессии:

Уравнение регрессии:

y_х=a₀+a₁*x

y_х=41,83 – 5,2x.

Теснота связи:

D = 0,3969

Таким образом, связь между урожайностью и себестоимостью по шкале Чэддека достаточная или средняя. Оценка линейного коэффициента корреляции показывает, что связь прямая, т. е. с увеличением урожайности увеличивается и себестоимость 1ц. зерна (сахарной свеклы, подсолнечника).

Выводы и предложения

В ходе решения задач курсовой работы получены следующие результаты:

Себестоимость и производственные затраты — важнейшие результативные показатели растениеводства и сельскохозяйственного производства в целом. Уровень себестоимости отражает воздействие экономических и приходных условий, в которых осуществляется сельскохозяйственное производство, и качество организационно-хозяйственной деятельности каждого предприятия.

Производственные затраты характеризуют общий объем затрат производства продукции данной культуры, а себестоимость — стоимостную оценку этой культуры в конкретных условиях ее возделывания.

Динамика производственных затрат характеризуется общим подъемом на 20,3% за исследуемый период. При этом как цепные так и базисные показатели темпов прироста имеют преимущественно положительное значение, что позволяет характеризовать динамику как общее подъем производственных затрат.

С помощью методов выравнивания выявлена общая тенденция подъема себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период.

Динамика себестоимости зерна (сахарной свеклы, подсолнечника) за исследуемый период носит устойчивую тенденцию к повышению, при этом локальная колебимость признака, имеющая место в 2000, 2003 и 2004 годах не оказала существенного влияния на общие результаты выравнивания, а значит, является статистически малозначимой.

Все экономические индексы можно классифицировать по следующим признакам:

• степень охвата явления;

• база сравнения;

• вид весов (соизмерителя);

• форма построения;

• характер объекта исследования:

• объект исследования;

• состав явления;

• период исчисления.

Средняя себестоимость 1 ц. зерна (сахарной свеклы, подсолнечника) в отчетном году по сравнению с базисным увеличилась на 44,31 или на 40 %.

За счет увеличения себестоимости 1 ц. продукции в отдельных хозяйствах производственные затраты увеличились на ц или на 37 %. За счет улучшения структуры произведенной продукции производственные затраты увеличилась на ц или на 2 %. За счет уменьшения количества произведенной продукции производственные затраты уменьшились на 1542393,94 ц. или на 3 %

Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок: типологические, структурные, аналитические.

С помощью корреляционно-регрессионного исследования выявлено, что связь между себестоимостью и урожайностью средняя. Оценка линейного коэффициента корреляции показывает, что связь прямая, т. е. с увеличением урожайности увеличивается и себестоимость 1ц. зерна (сахарной свеклы, подсолнечника).

Список литературы

Адамов В.К. Факторный индексный анализ (Методология и проблемы). ML: Статистика. 2005.- 200 с.
Альбом наглядных пособий по общей теории статистики: Учеб. пособие. М.: Финансы и статистика, 2005.- 80 с.
Анализ финансово-экономической деятельности предприятия: Учеб. Пособие для ВУЗов/под ред. Любушина Н.П. –М.: ИНИТИ – ДАНА, 2005.- 471с.
Баканов М.И., Шеремет А.Д. Теория анализа хозяйственной деятельности Учебник, 3-е переработанное и дополненное издание: М.: Финансы и статистика. 2007. – 489 с.
Вучков И. и др. Прикладной линейный регрессионный анализ / Пер. с болг. И. Вучков, Л. Бояджиева, Е. Солжов. М: Финансы и статистика, 2008.- 239 с.
Долгушевский Ф.Г., Христич А.Г. Сельскохозяйственная статистика с основами экономической статистики. М.: Статистика, 2006. – 311 с
Елисеева И.И. Общая теория статистики. М. Финансы и статистика. 2007. – 287 с
Емельянов A.M. Экономика сельского хозяйства М.: Экономика. 2007. – 290 с.
Ефимова М.Р., Рябцев В.М. Общая теория статистики: Учебник. М.: Финансы и статистика, 2005.- 303 с.
Кравченко Л.И. Анализ финансового состояния предприятия. М.: ЮНИТИ. 2006. – 450 с.
Крастин О.П. Разработка и интерпретация моделей корреляционных связей в экономике. - Рига: Зинатне, 2007. – 408 с.
Маркин Ю.П. Анализ внутрихозяйственных резервов. М: Финансы и статистика,2005. – 379 с.
Муравьев А.И. Теория экономического анализа: проблемы и решения. М: Финансы и статистика,2008. – 391 с.
Панков Д.А. Современные методы анализа финансового положения М.: ООО Профит.2005. – 233 с.
Плошка Б.Г. Группировка и система статистических показателей. М.: Статистка, 2005.- 176 с.
Рафиков М.М. Экономика, организация и планирование сельскохозяйственного производства. M: Экономика, 2008. – 411 с.
Савицкая Г.В. Теория анализа хозяйственной деятельности М: ИСЗ, 2005. -220 с.
Савицкая Г.В. Анализ хозяйственной деятельности промышленного предприятия. М.: ИСЗ, 2005. – 109 с.
Сергеев С.С. Сельскохозяйственная статистика с основами экономической статистики. М.: Финансы и статистика, 2005. – 89 с.
Статистическое моделирование и прогнозирование / Под ред. А.Г. Гранберга. М.: Финансы и статистика, 2006.- 383 с.
Стражев В.Н. Оперативное управление предприятием, проблемы учета и анализа Мн.: Наука и техника,2007. – 330 с.
Теория экономического анализа (под ред. Шеремета А.Д. М.: Прогресс. 2006. – 590 с.
Шеремет А.Д. Методика финансового анализа предприятияМ.: ИПО МП, 2006. – 450 с.
Экономика предприятия Под. ред.проф. В.Я. Горфинкеля, М.,2006. – 189 с.

Листать вверх Листать вниз

Получить код

Скачать материал (0.12 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории экономика:

Определение спроса и предложения на рынке гофроящиков

Аналіз ТОВ АФ ім. Гагаріга Зміївського району Харківської області

Финансовые результаты деятельности организации, оказывающей платные услуги, и пути их увеличения (на материалах КТСУП "Отель")

Правовое регулирование деятельности совместных предприятий на территории Российской Федерации

Теневая экономика как глобальная проблема

Анализ трудовых ресурсов главного сборочного цеха тракторного завода

Основи економіки підприємства малого бізнесу