Статистическое исследование регионов РФ

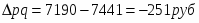
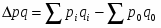
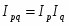
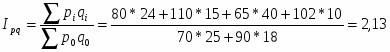
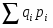
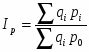
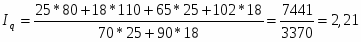
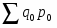
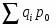
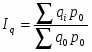
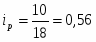
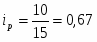
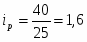
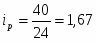
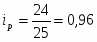
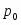
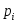
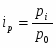
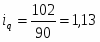
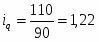
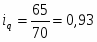
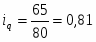
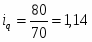
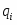
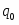
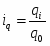
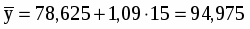
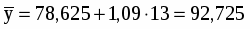
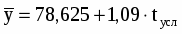
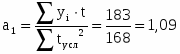
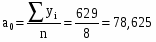
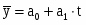
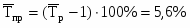
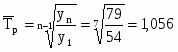
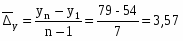
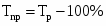
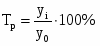
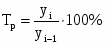
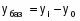
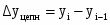
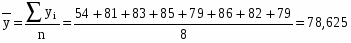
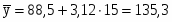
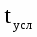
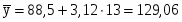
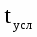
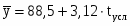
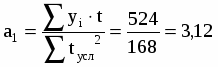
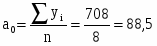
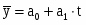
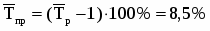
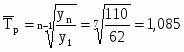
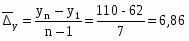
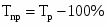
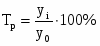
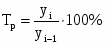
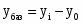
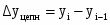
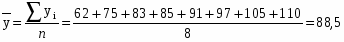
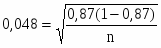
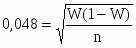
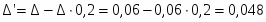
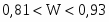
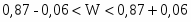
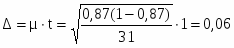
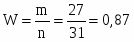
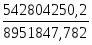
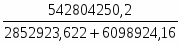
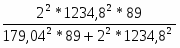
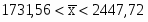
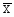
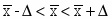
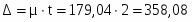
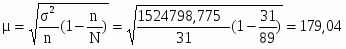
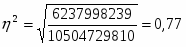
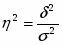
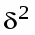
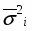
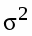
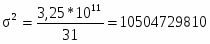
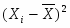
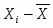
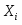
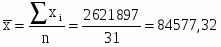
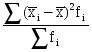
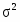
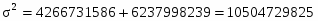
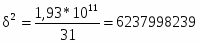
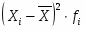
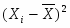
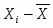
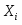
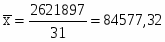
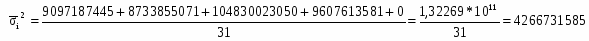
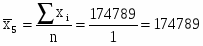
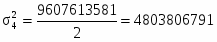
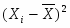
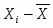
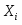
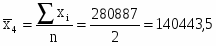
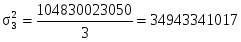
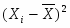
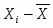
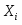
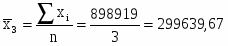
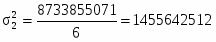
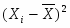
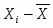
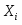
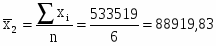
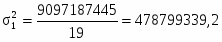
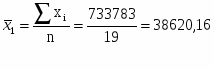
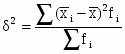
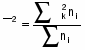
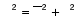
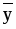
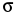
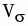
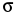
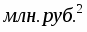
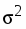
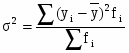
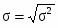
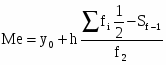
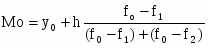
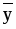
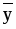
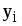
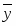
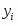
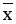
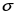
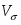
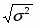
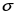
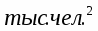
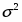
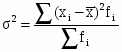
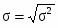
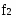
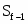
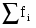
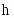
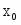
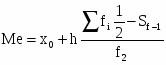
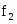
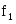
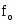
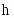
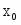
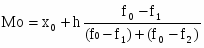
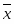
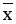
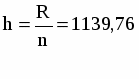Кафедра экономики и управления на предприятии

КУРСОВАЯ РАБОТА

Дисциплина: "Статистика"

Тема: «Статистическое исследование регионов РФ»

Вариант № 77

2008

Содержание

1. Задание №1

2. Задание №2

3. Задание №3

4. Задание №4

5. Задание №5

Список литературы

1. Задание №1

Таблица 1.1 Исходные данные - социально-экономические показатели по регионам России, 2002 год (10-40 интервал наблюдения; 1 и 4 признак)

Регионы

Численность постоянного населения на конец года, тыс. чел.

Объём промышленной продукции, млн. руб.

Московская обл.

6409,7

174789

Орловская обл.

883,5

16327

Рязанская обл.

1255,0

30406

Смоленская обл.

1098,3

32639

Тамбовская обл.

1240,7

15127

Тверская обл.

1552,3

38174

Тульская обл.

1690,0

59320

Ярославская обл.

1386,3

60425

Республика Карелия

756,4

29994

Республика Коми

1117,2

68499

Архангельская обл.

1428,9

43512

Вологодская обл.

1301,1

88196

Калининградская обл.

943,2

18199

Ленинградская обл.

1649,6

74326

Мурманская обл.

977,6

51639

Новгородская обл.

710,9

23959

Псковская обл.

778

11916

Нижегородская обл.

3598,3

125957

Краснодарский край

4987,6

71134

Ставропольский край

2642,6

37634

Оренбургская обл.

2199,4

66707

Пензенская обл.

1504,1

22226

Пермская обл.

2923,7

143321

Самарская обл.

3258,7

213881

Саратовская обл.

2676,4

55840

Ульяновская обл.

1439,6

32579

Курганская обл.

1074,4

16320

Свердловская обл.

4544,9

209753

Тюменская обл.

3272,2

559081

Иркутская обл.

2712,9

105129

Кемеровская обл.

2940,5

124888

1.1 Структурная равноинтервальная группировка

1.1.1 Структурная группировка по признаку – численность постоянного населения на конец года, тыс. чел.

X- численность постоянного населения на конец года, тыс. чел.

Y- Объём промышленной продукции, млн. руб.

Xmax=6409,7

Xmin=710,9

n=5

R=Xmax-Xmin =5698,8

Таблица 1.2 Группировка регионов по численности постоянного населения на конец года, тыс. чел.

№ п/п

Группы регионов по численности постоянного населения на конец года, тыс. чел.

Количество регионов

в группе

Процент к итогу, %

710,9 – 1850,66

61,3

1850,66 – 2990,42

19,3

2990,42 – 4130,18

9,7

4130,18 – 5269,94

6,5

5269,94 – 6409,7

3,2

Итого

100

Вывод: максимальное количество регионов 19 из 31(61,3 %) имеют численность населения занятых в экономике, лежащую в пределах от 710,9 до 1850,66 тыс. чел. Затем, 6 регионов: Ставропольский край, Оренбургская обл., Пермская обл., Саратовская обл., Иркутская обл., Кемеровская обл., (19,3%) имеют численность населения занятых в экономике, лежащую в пределах от 1850,66 до 2990,42 тыс. чел. Среди регионов с самой большой численностью выделяется Московская обл. – 6409 тыс. чел.

1.1.2 Структурная группировка по признаку - объём промышленной продукции, млн. руб.

Ymax=559081

Ymin=11916

n=6

R=547165

h=91194,17

Таблица 1.3 Группировка регионов России по объёму промышленной продукции, млн. руб. в 2002 г.

№ п/п

Группы регионов по объёму промышленной продукции, млн. руб.

Количество регионов

в группе

Процент к итогу, %

11916 – 103110,17

77,4

103110,17 – 194304,34

19.4

194304,34 – 285498,51

285498,51 – 376692,68

376692,68 – 467886,85

467886,85 - 559081

3,2

Итого:

100

Вывод: максимальное количество регионов 24 из 31(77,4%) производит промышленной продукции в интервале от 11916 до103110,17 млн. руб. Тюменская область производит больше всего промышленной продукции: 559081 млн. руб.

1.2 Аналитическая группировка

В качестве признака фактора выберем численность населения занятое в экономике, а в качестве результата – объём промышленной продукции, так как население производит эту промышленную продукцию.

Таблица 1.4 Распределение регионов по численности постоянного населения на конец года, тыс. чел. и объёму промышленной продукции, млн. руб.

Группы регионов по численности постоянного населения, тыс. чел.

Количество регионов

в группе

Итого по объёму промышленной продукции, млн. руб.

Среднее значение объёма промышленной продукции, млн. руб.

710,9 – 1850,66

733783

38620,16

1850,66 – 2990,42

533519

88919,83

2990,42 – 4130,18

898919

299639,67

4130,18 – 5269,94

280887

140443,5

5269,94 – 6409,7

174789

Итого

2621897

84577,32

Вывод: Поскольку не существует четкой взаимосвязи между значениями признаков, связь между ними – скачкообразная слабая.

1.3 Комбинационная группировка

Таблица 1.5 Комбинационная группировка

Группы регионов по численности постоянного населения, тыс. чел.

Группы регионов по объёму промышленной продукции, млн. руб.

11916 – 103110,17

103110,17 – 194304,34

194304,34 – 285498,51

285498,51 – 376692,68

376692,68 – 467886,85

467886,85 - 559081

Итого

710,9 – 1850,66

1850,66 – 2990,42

2990,42 – 4130,18

4130,18 – 5269,94

5269,94 – 6409,7

Итого

Вывод: Т.к. наибольшие частоты не расположены вдоль диагонали, идущей из левого верхнего угла к правому нижнему, то связь между признаками - скачкообразная слабая.

2. Задание №2

2.1 Построение рядов распределения

2.1.1 Ряд распределения регионов по численности постоянного населения на конец года, тыс. чел.

Таблица 2.1 Распределение регионов по численности постоянного населения на конец года, тыс. чел.

№ п/п

Группы регионов по численности постоянного населения, тыс. чел.

Число регионов, единиц fi

Накопленные частоты S

710,9 – 1850,66

1850,66 – 2990,42

2990,42 – 4130,18

4130,18 – 5269,94

5269,94 – 6409,7

Итого:

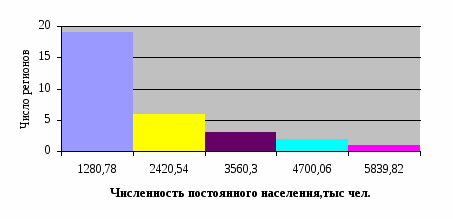
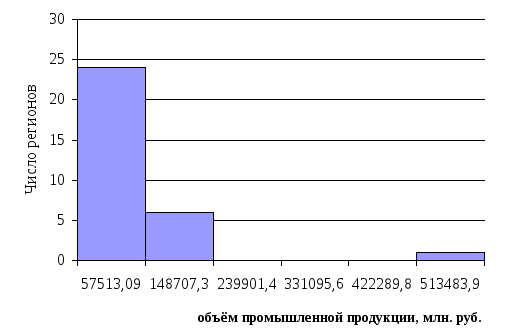
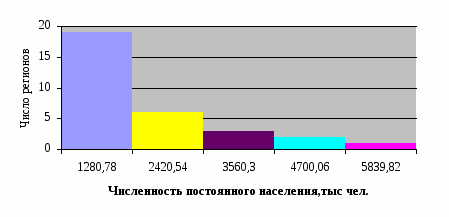
Рис. 2.1 Гистограмма распределения регионов по численности постоянного населения на конец года, тыс. чел.

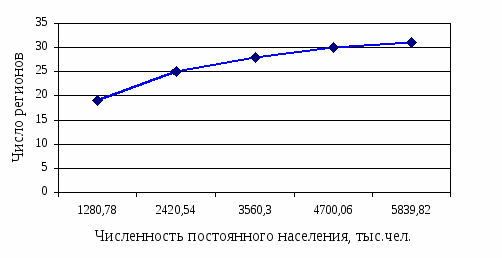
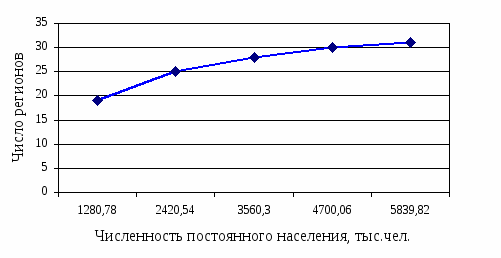
Рис. 2.2 Кумулятивное распределение регионов по численности постоянного населения на конец года, тыс. чел

2.1.2 Ряд распределения регионов по объёму промышленной продукции, млн. руб.

Таблица 2.2

Распределение регионов по объёму промышленной продукции, млн. руб. в 2002 г.

Группы регионов по объёму промышленной продукции, млн. руб.

Число регионов, единиц fi

Накопленные частоты S

11916 – 103110,17

103110,17 – 194304,34

194304,34 – 285498,51

285498,51 – 376692,68

376692,68 – 467886,85

467886,85 - 559081

Итого:

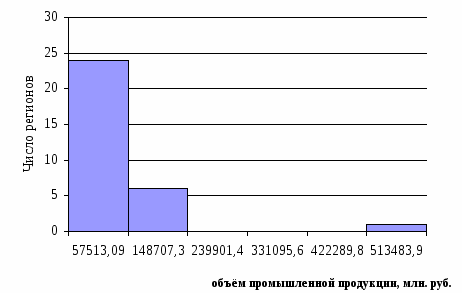
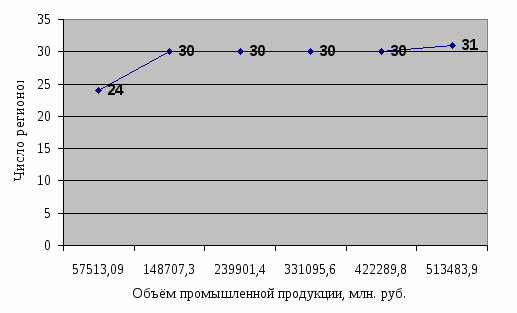
Рис. 2.3 Гистограмма распределения регионов по объёму промышленной продукции, млн. руб.

Рис. 2.4 Кумулятивное распределение регионов по объёму промышленной продукции, млн. руб.

2.2 Анализ рядов распределения

2.2.1 Анализ ряда распределения регионов по численности постоянного населения на конец года, тыс. чел

Таблица 2.3 Распределение регионов по численности постоянного населения на конец года, тыс. чел.

№ п/п

Группы регионов по численности постоянного населения на конец года, тыс. чел.

Число регио-

нов, единиц fi

Сере

дины интервалов xi

Накопленные частоты S

xi fi

Ixi - I

Ixi - I2 fi

710,9-1850,66

1280,78

24334,82

808,86

12430835,49

1850,66-2990,42

2420,54

14523,24

330,90

656968,86

2990,42-4130,18

3560,30

10680,90

1470,66

6488522,51

4130,18-5269,94

4700,06

9400,12

2610,42

13628585,15

5269,94-6409,7

5839,82

3750,18

14063850,03

Итого:

64778,90

47268762,04

Среднее арифметическое значение признака:

=64778,90/31=2089,64

Вывод: По данным по 31 региону в 2002г средняя численность постоянного населения на конец года составляет 2089,64 тыс. чел.

Мода:

- начало модального интервала

- величина интервала

- частота модального интервала

- частота интервала предшествующего модальному

- частота интервала последующему модальному

Mo=710, 9+1139,76*((19-0)/((19-0)+(19-6)))=1387,6

Рис. 2.5. Графическое представление моды с помощью гистограммы распределения численности постоянного населения на конец года, тыс.чел.

Вывод: большинство регионов имеют численность постоянного населения на конец года 1387,6 тыс. чел. в 2002г.

Медиана:

- начало медианного интервала

- величина интервала

- сумма частот

- накопленная частота ряда, предшествующего медианному

- частота медианного интервала

Me=710, 9+1139,76*((31/2-0)/19)=1640,7

Рис. 2.6 Графическое представление медианы с помощью кумуляты распределения численности постоянного населения на конец года, тыс.чел.

Вывод: половина регионов имеет численность постоянного населения в 2002г. менее 1640,7 тыс. чел., другая половина имеет численность более 1640,7 тыс. чел.

Среднеквадратическое отклонение:

=47268762,04/31=1524798,775 ()

==1234,8(тыс. чел.)

Вывод: возможное отклонения численность постоянного населения на конец года от средней численности постоянного населения составляет 1234,8 тыс. чел.

Коэффициент вариации:

=/*100%=(1234,8/2089,64)*100%=59,1%

Вывод: совокупность не однородна, так как коэффициент вариации превышает 33%

2.2.2 Анализ ряда распределения регионов по объёму промышленной продукции, млн. руб.

Таблица 2.2 Распределение регионов по объёму промышленной продукции, млн. руб.

Группы регионов по объёму промышленной продукции, млн. руб.

Число регионов, единиц fi

Середины интервалов yi

Накопленные частоты S

Iyi -I

I-I 2 fi

11916 – 103110,17

57513,09

1380314,16

32359,23

25130874388,63

103110,17 – 194304,34

148707,3

892243,8

58834,98

20769329229,60

194304,34 – 285498,51

239901,4

150029,08

285498,51 – 376692,68

331095,6

241223,28

376692,68 – 467886,85

422289,8

332417,48

467886,85 - 559081

513483,9

423611,58

179446770710,10

Итого:

2786041,86

225346974328,33

Среднее арифметическое значение признака:

=2786041,86/31=89872,32 (млн. руб.)

Вывод: среднее производство промышленной продукции в год составляет 89872,32 млн. руб.

Мода:

Mo=11916+9194,17*((24-0)/((24-0)+(24-6)))=17169,8 млн. руб.

Рис. 2.7. Графическое представление моды с помощью гистограммы распределения объёма промышленной продукции, млн. руб.

Вывод: большинство регионов производит промышленной продукции - 17169,8 млн. руб.

Медиана:

Me=11916+9194,17*((31/2-0)/24) =17853,9 млн. руб.

Рис. 2.8. Графическое представление медианы с помощью кумуляты распределения объёма промышленной продукции, млн. руб..

Вывод: половина регионов производит промышленной продукции более 17853,9 млн. руб., другая половина - менее 17853,9 млн. руб.

Среднеквадратическое отклонение:

=225346974328,33/31=7269257236,40 ()

==85259,93922 млн. руб.

Вывод: возможное отклонения объёма промышленной продукции от среднего объёма промышленной продукции составляет 85259,93922 млн. руб. (в год)

Коэффициент вариации:

=/*100%=85259,93922 /89872,32 *100%=95%

Вывод: совокупность не однородна, так как коэффициент вариации превышает 33%

2.3 Проверка теоремы о разложении дисперсии

По 1 группе:

Таблица 2.3 Промежуточные показатели

16327

-22293,16

496984982,8

30406

-8214,16

67472424,51

32639

-5981,16

35774274,95

15127

-23493,16

551928566,8

38174

-446,16

199058,7456

59320

20699,84

428483376

60425

21804,84

475451047,4

29994

-8626,16

74410636,35

68499

29878,84

892745079,7

43512

4891,84

23930098,59

88196

49575,84

2457763912

18199

-20421,16

417023775,7

74326

35705,84

1274907010

51639

13018,84

169490194,9

23959

-14661,16

214949612,5

11916

-26704,16

713112161,3

22226

-16394,16

268768482,1

32579

-6041,16

36495614,15

16320

-22300,16

497297136

Итого

9097187445

По 2 группе:

Таблица 2.4 Промежуточные показатели

37634

-51285,83

2630236359

66707

-22212,83

493409816,6

143321

54401,17

2959487297

55840

-33079,83

1094275153

105129

16209,17

262737192,1

124888

35968,17

1293709253

Итого

8733855071

По 3 группе:

_{Таблица 2.5}_{Промежуточные результаты}

125957

-173682,67

30165669858

213881

-85758,67

7354549480

559081

259441,33

67309803712

Итого

104830023050

По 4 группе:

_{Таблица 2.6}_{Промежуточные результаты}

71134

-69309,5

4803806790

209753

69309,5

4803806790

Итого

9607613581

По 5 группе:

_{Таблица 2.7}_{Промежуточные результаты}

174789

Итого

Средняя из внутригрупповых дисперсий:

Межгрупповая дисперсия:

Таблица 2.8 Промежуточные показатели

38620,16

-45957,16

2112060555

40129150550

88919,83

4342,51

18857393,1

113144358,6

299639,67

215062,35

46251814388

1,38755E+11

140443,5

55866,18

3121030068

6242060136

174789

90211,68

8138147208

Итого

1,93*1011

Общая дисперсия по правилу сложения:

Общая дисперсия по формуле:

Среднее значение дисперсии:

Таблица 2.9 Промежуточные показатели

174789

90211,68

8138147208

16327

-68250,32

4658106180

30406

-54171,32

2934531911

32639

-51938,32

2697589084

15127

-69450,32

4823346948

38174

-46403,32

2153268107

59320

-25257,32

637932213,6

60425

-24152,32

583334561,4

29994

-54583,32

2979338822

68499

-16078,32

258512374

43512

-41065,32

1686360507

88196

3618,68

13094844,94

18199

-66378,32

4406081366

74326

-10251,32

105089561,7

51639

-32938,32

1084932924

23959

-60618,32

3674580720

11916

-72661,32

5279667424

125957

41379,68

1712277917

71134

-13443,32

180722852,6

37634

-46943,32

2203675293

66707

-17870,32

319348336,9

22226

-62351,32

3887687106

143321

58743,68

3450819940

213881

129303,68

16719441662

55840

-28737,32

825833560,8

32579

-51998,32

2703825283

16320

-68257,32

4659061734

209753

125175,68

15668950863

559081

474503,68

2,25154E+11

105129

20551,68

422371550,8

124888

40310,68

1624950922

Итого

3,25647E+11

=+-Теорема о разложении дисперсии.

10504729810 = 6237998239+4266731585 = 10504729824

Из проведённых расчётов видно, что общие дисперсии, рассчитанные различными способами, имеют небольшое отклонение, что и требовалось доказать.

2.4 Найти коэффициент детерминации

Вывод: фактор численности постоянного населения повлиял на производство промышленной продукции на 77%.

3. Задание №3

3.1.а Пределы, за которые не выйдет среднее значение признака

Т.к. по условию отбор – 35% бесповторный, и объем выборочной совокупности – 31 элементов, то объем генеральной совокупности будет равен 89 элементов(N). Т.к. p=0,954, то t=2.

Средняя ошибка выборки:

Предельная ошибка выборки:

Таким образом:

=2089,64

Вывод: с вероятностью 0,954 можно утверждать, что численность постоянного населения на конец года колеблется в пределах 1731,56 – 2447,72 тыс. чел.

3.1.б Определение объема выборки для снижения предельной ошибки средней величины на 50%

Т.к. коэффициент доверия в данном случае является постоянным, то при снижении предельной ошибки выборки на 50% средняя ошибка выборки также уменьшится на 50%.

n = t²²N/(Δ²N + t²²), где:

n – объём выборочной совокупности;

t - коэффициент доверия;

- среднее квадратическое отклонение;

N – объём генеральной совокупности;

Δ – предельная ошибка выборки;

t=2

Предельная ошибка равна 358,08 тыс. чел., если мы её снизим на 50% то она будет равна 179,04 тыс. чел.

Объём выборочной совокупности n = 31, после снижения предельной ошибки на 50% n – изменится.

n = = = = 60,636

Вывод: Объем выборочной совокупности необходимо увеличить до 60,636 (61) элементов.

3.2.а Определение пределов, за которые не выйдет значение доли предприятий с индивидуальными значениями, превышающими моду

В данном случае отбор повторный, выберем p=0,683; тогда t=1; количество предприятий с индивидуальными значениями признака, превышающими моду, равно 27.

Mo=17169,8 кг

Их доля равна:

Предельная ошибка выборки равна:

Таким образом:

т.е.:

Вывод: значение доли предприятий с индивидуальными значениями, превышающими моду, находятся в интервале от 0,81% до 0,93%.

3.2.б Определение объема выборки для снижения предельной ошибки доли на 20%

Предельная ошибка выборки:

Имеем:

тогда n=49,1

Вывод: для снижения предельной ошибки на 20% необходимо увеличить объем выборки до 49,1 (49) элементов.

4. Задание №4

4.1 Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях в Псковском районе (на 100 мест приходится детей)

Таблица 4.1 Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей)

Год

Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей)

Абсолютные приросты, чел. Δy

Темпы роста,% Тр.

Темпы прироста,% Тпр.

цепн.

базисн.

цепн.

базисн.

цепн.

базисн.

1999

100,0

2000

121

2001

110,7

133,9

10,7

33,9

2002

102,4

137,1

2,4

37,1

2003

107,1

146,8

7,1

46,8

2004

106,6

156,5

6,6

56,5

2005

105

108,2

169,3

8,2

69,3

2006

110

104,8

177,4

4,8

77,4

Итого

708

Среднегодовой уровень динамики:

Выбираем формулу для интервального равноотстоящего ряда среднегодового уровня динамики.

Абсолютный прирост:

на цепной основе:

на базисной основе:

Абсолютный прирост характеризует размер изменения ряда за период времени.

Темп роста:

на цепной основе:

на базисной основе:

Темп роста показывает во сколько раз данный уровень ряда больше(меньше) базисного (предыдущего) или какую часть его составляет.

Темп прироста:

Темп прироста показывает, на сколько процентов уровень ряда больше (меньше) базисного (предыдущего). Средний абсолютный прирост:

Средний темп роста:

Средний темп прироста:

Вывод: на основе полученных данных можно сделать вывод о том, что по Псковскому району самый высокий уровень обеспеченности местами детей, находящихся в дошкольных учреждениях был зарегистрирован в 2006 году – 110 человек на 100 мест, самый низкий в 1999 году – 62 человека на 100 мест. С 1999 года по 2006 год обеспеченность местами детей, находящихся в дошкольных учреждениях возрастает. В 2006 году уровень обеспеченности местами детей, находящихся в дошкольных учреждениях составляет 77,4% от уровня 1999 года

Из расчетов видно, что в среднем за год идёт прирост обеспеченности местами детей, находящихся в дошкольных учреждениях в Псковском районе – на 6,86 чел.

Таблица 4.2 Сглаживание ряда динамики трехлетней скользящей средней

Года

Район

1999

2000

2001

2002

2003

2004

2005

2006

Псковский

105

110

Трехлетняя скользящая средняя

73,3

86,3

97,7

104

Таблица 4.3 Аналитическое выравнивание ряда

Год

Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей)

tусл

(tусл)2

yitусл

3,12tусл

yср

1999

-7

-434

-21,84

66,66

2000

-5

-375

-15,6

72,9

2001

-3

-249

-9,36

79,14

2002

-1

-85

-3,12

85,38

2003

3,12

91,62

2004

291

9,36

97,86

2005

105

515

15,6

104,1

2006

110

770

21,84

110,34

Итого:

708

168

524

Уравнение прямой:

a₀ – характеризует средний уровень ряда динамики

a₁ – характеризует изменение ускорения

Тогда

Сделаем прогноз динамики обеспеченности местами детей, находящихся в дошкольных учреждениях в Псковском районе на 2009 год:

=13

детей приходится на 100 мест

на 2010 год:

=15

детей приходится на 100 мест

Таким образом, мы видим, что обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) в Псковском районе будет повышаться и в дальнейшем.

Рис. 4.1. Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) в Псковском районе

4.2 Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях в Усвятском районе (на 100 мест приходится детей)

Таблица 4.4 Динамика обеспеченности местами детей, находящихся в дошкольных учреждениях в Усвятском районе (на 100 мест приходится детей).

Год

Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) yi

Абсолютные приросты, чел. Δy

Темпы роста,% Тр.

Темпы прироста,% Тпр.

цепн.

базисн.

цепн.

базисн.

цепн.

базисн.

1999

2000

150

2001

102,5

153,7

2,5

53,7

2002

102,4

157,4

2,4

57,4

2003

-6

92,9

146,3

-7,1

46,3

2004

108,9

159,3

8,9

59,3

2005

-4

95,3

151,8

-4,7

51,8

2006

-3

96,3

146,3

-3,7

46,3

Итого

629

Среднегодовой уровень динамики:

Абсолютный прирост:

на цепной основе:

на базисной основе:

Абсолютный прирост характеризует размер изменения ряда за период времени.

Темп роста:

на цепной основе:

на базисной основе:

Темп прироста:

Темп прироста показывает на сколько процентов уровень ряда больше(меньше) базисного (предыдущего).

Средний абсолютный прирост:

Средний темп роста:

Средний темп прироста:

Вывод: на основе полученных данных можно сделать вывод о том, что по Усвятскому району самый высокий уровень обеспеченности местами детей, находящихся в дошкольных учреждениях, был зарегистрирован в 2004 году – 86 человек на 100 мест, самый низкий в 1999 году – 54 человека на 100 мест. В 2006 году уровень обеспеченности местами детей, находящихся в дошкольных учреждениях, составляет 146,3% от уровня 1999 года.

Из расчетов видно, что в среднем за год идёт рост обеспеченности местами детей, находящихся в дошкольных учреждениях в Усвятском районе на 3,57 чел.; темп прироста положительный – 5,6%.

Таблица 4.5 Сглаживание ряда динамики трехлетней скользящей средней

Года

Район

1999

2000

2001

2002

2003

2004

2005

2006

Невельский

Трехлетняя скользящая средняя

72,7

82,3

83,3

82,3

Таблица 4.6 Аналитическое выравнивание ряда

Год

Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей)

tусл

(tусл)2

yitусл

1,09tусл

yср

1999

-7

-378

-7,63

70,995

2000

-5

-405

-5,45

73,175

2001

-3

-249

-3,27

75,355

2002

-1

-85

-1,09

77,535

2003

1,09

79,715

2004

258

3,27

81,895

2005

410

5,45

84,075

2006

553

7,63

86,255

Итого:

629

168

183

Уравнение прямой:

a₀ – характеризует средний уровень ряда динамики

a₁ – характеризует изменение ускорения

Вывод: Обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) ежегодно в среднем составляет 79 человек; численность в периоде в среднем ежегодно увеличивается на 1 человека.

Тогда

Сделаем прогноз динамики обеспеченности местами детей, находящихся в дошкольных учреждениях в Усвятском районе (на 100 мест приходится детей).на 2009, 2010 года

на 2009 год:

=13

человек

на 2010 год:

=15

человек

Таким образом мы видим, что обеспеченность местами детей, находящихся в дошкольных учреждениях (на 100 мест приходится детей) в районе будет в дальнейшем расти.

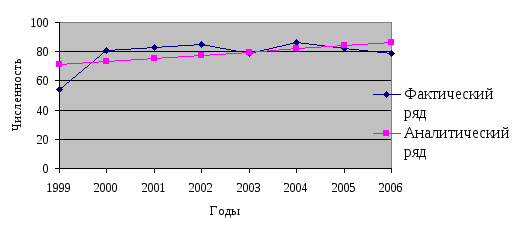
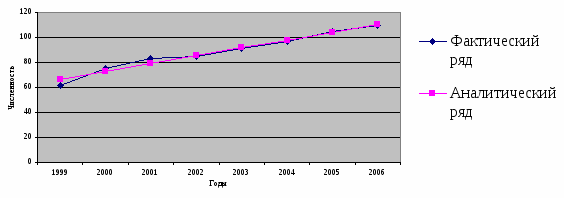
Рис 4.4 Фактический и выровненный динамические ряды

Сравнивая показатели обеспеченности местами детей, находящихся в дошкольных учреждениях в Псковском и Усвятском районах, можно сделать следующий вывод: с 1999 года обеспеченность местами детей, находящихся в дошкольных учреждениях, как в Усвятском так и Псковском районе колеблется. Эта тенденция характерна для двух районов. Из прогноза видна тенденция повышения обеспеченности местами детей, находящихся в дошкольных учреждениях.

5. Задание №5

5.1 Исходные данные

Таблица 5.1 Цена и количество проданного товара.

Вид товара

1 квартал

2 квартал

3 квартал

Продано тыс.кг

Цена за 1кг, руб

Продано тыс. кг

Цена за 1кг, руб

Продано тыс. кг

Цена за 1кг, руб

Яблоки

морковь

110

102

5.2 Индивидуальные индексы

5.2.1 Индивидуальные индексы объема проданного товара

, где

- это объем товаров в натуральном выражении в базисном периоде

- это объем товаров в натуральном выражении в i-ом периоде

Рассчитаем индивидуальные индексы физического объема по яблокам:

Вывод: объём продаж яблок во 2-ом квартале увеличился на 14% по сравнению с 1-ым кварталом.

Вывод: объём продаж яблок в 3 квартале уменьшился на 19% по сравнению со 2 кварталом.

Вывод: объём продаж яблок в 3 квартале уменьшился на 3% по сравнению с 1 кварталом.

Рассчитаем индивидуальный индекс физического объема по моркови:

Вывод: объём продаж моркови во втором квартале увеличился на 22% по сравнению с первым.

Вывод: объём продаж моркови в 3 квартале уменьшился на 7% по сравнению со 2 кварталом

Вывод: объём продаж моркови в 3 квартале увеличился на 13% по сравнению с 1 кварталом.

5.2.2Индивидуальный индекс цен

, где

- цена единицы товара в i-ом периоде

- цена единицы товара в базисном периоде

Рассчитаем индивидуальные индексы цен по яблокам:

Вывод: цена яблок во 2 квартале уменьшилась на 4% по сравнению с 1 кварталом.

Вывод: цена яблок в 3 квартале увеличилась на 67% по сравнению со 2 кварталом.

Вывод: цена яблок в 3квартале увеличилась на 60% по сравнению с 1 кварталом.

Рассчитаем индивидуальные индексы цен по моркови:

Вывод: цена моркови во 2 квартале уменьшилась на 17% по сравнению с 1 кварталом.

Вывод: цена моркови в 3 квартале уменьшилась в 0,67 раз по сравнению со 2 кварталом.

Вывод: цена моркови в 3 квартале уменьшилась на 44% по сравнению с 1 кварталом.

5.3 Общий индекс

5.3.1 Индекс физического объема товарооборота

, где

- стоимость произведенных в i-ом периоде товаров в ценах базисного периода.

- фактическая стоимость товаров, произведенных в базисном периоде.

Вывод: изменение стоимости товаров произошло в 2,21 раз (цены товаров считаются постоянными).

5.3.2 Общий индекс цен

, где

- фактическая стоимость товаров, производимых в i-ом периоде.

Вывод: стоимость товаров уменьшилась на 3% (объем проданных товаров считается постоянным).

5.3.3 Общий индекс товарооборота

Вывод: изменение стоимости товаров, обусловленное увеличением цен на яблоки, произошло в 2,13 раза.

Покажем взаимосвязь между индексами:

2,13=0,97*2,21

2,13=2,13

Вывод: таким образом, мы показали связь между общими индексами физического объема товарооборота, цены и товарооборота.

5.4 Прирост товарооборота - всего и в том числе за счет изменения цен и объема продажи товаров

Прирост товарооборота:

Вывод: за счет роста цен на яблоки, стоимость товаров за рассматриваемый период увеличилась на 3820 руб.

Вывод: за счет уменьшения цен на морковь, стоимость товаров за рассматриваемый период уменьшилась на 251 руб.

Список литературы

Районы Псковской области: ст. сборник в 2 томах, Псковоблкомстат, 1999.-115 с., том 1
Районы Псковской области: социально-экономические показатели, Псковоблкомстат, 2005.-212 с.
Теория статистики: Учебник/Под ред. проф. Р.А. Шмойловой. – 3-е изд.,. перераб. – М.: Финансы и статистика, 2002. –560 с.: ил.
Методические указания по выполнению курсовой работы по ред. Л.Н. Гальдикас и Л.И. Стрикуновой., 2004 г.

Листать вверх Листать вниз

Получить код

Скачать материал (0.16 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории экономика:

Оценка современного состояния и проблем развития АПК Республики Беларусь

Цены и ценообразование в общественном питании

Строительный комплекс в новых экономических условиях

Статистичні спостереження

Совершенствование организации и управления деятельностью ООО "Инжстрой-Сити Монолит"

Облік цінних паперів 62

Развитие методов экспертизы инновационных проектов и решений