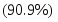
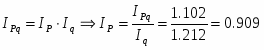
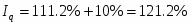
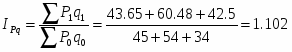
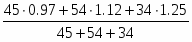
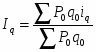
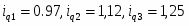
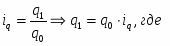
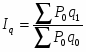
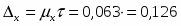
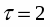
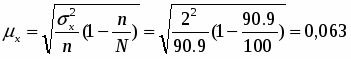
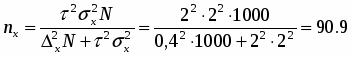
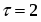
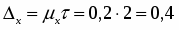
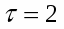
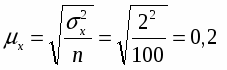
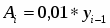
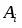
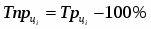
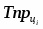
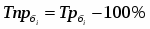
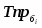
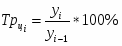
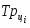
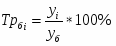
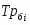
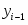
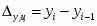
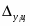
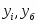
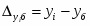
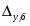
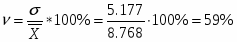
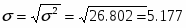
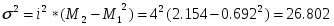
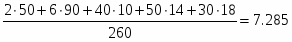
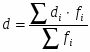
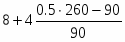
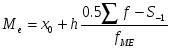
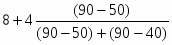
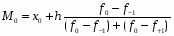
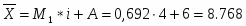
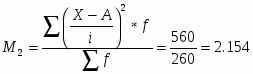
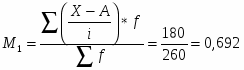
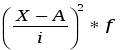
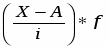
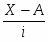
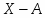
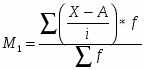
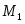
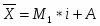
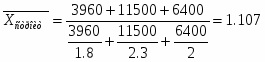
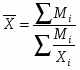
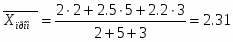
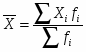
Задача 1.7

Имеются данные по группе работников промышленного предприятия

№ п/п

Выполнение норм выработки, %

Заработная плата грн.

№ п/п

Выполнение норм выработки, %

Заработная плата грн.

1

103,1

363

16

107

388

2

105,2

382

17

105,8

389

3

106

390

18

97

340

4

96,7

342

19

103

364

5

114

416

20

108

395

6

107

404

21

110

410

7

98,5

344

22

100,8

362

8

90

300

23

105,3

385

9

102,3

373

24

103

376

10

106,4

378

25

93,6

303

11

104,3

367

26

100,7

363

12

103,7

364

27

98

345

13

106,9

387

28

101

356

14

94

310

29

101,2

360

15

108,3

406

30

100

350

Для изучения зависимости между выполнением норм выработки и заработной платы произведите группировку рабочих по выполнению норм выработки, выделив пять групп с равными интервалами. По каждой группе и в целом совокупности работников подсчитайте:

1) число рабочих;

2) средний процент выполнения норм;

3) среднюю заработную плату;

Результаты представьте в виде таблицы сделайте выводы.

Решение

Величина интервала

h = (x_max – x_min) / m = (114 – 90) / 5 = 4,8

Границы интервалов:

90 + 4,8 = 94,8

94,8 + 4,8 = 99,6

99,6 + 4,8 = 104,4

104,4 +4,8 = 109,2

109,2 + 4,8 =114

Следовательно, первая группа рабочих имеет норм выработки 90–94.8%, вторая – 94.8–99.6%, третья – 99,6–104,4%, четвертая – 104,4–109,2%, пятая – 109,2–114% выработки. По каждой группе подсчитаем нормы заработной платы и оформим результаты в виде рабочей таблицы 2.

Таблица 2

№ п/п

Выполнение норм выработки, %

Заработная плата грн.

8

90

300

25

93,6

303

14

94

310

Итого

277,6

913

4

96,7

342

18

97

340

27

98

345

7

98,5

344

Итого

390,2

1371

30

100

350

26

100,7

363

22

100,8

362

28

101

356

29

101,2

360

9

102,3

373

24

103

376

19

103

364

1

103,1

363

12

103,7

364

11

104,3

367

Итого

1123,1

3998

2

105,2

382

23

105,3

385

17

105,8

389

3

106

390

10

106,4

378

13

106,9

387

6

107

404

16

107

388

20

108

395

15

108,3

406

Итого

1065,9

3904

21

110

410

5

114

416

Итого

224

826

Построим аналитическую таблицу по группировочному признаку (см. таблицу 3).

Таблица 3

№ группы

Группа рабочих по выработке, %

Число рабочих, чел.

Средняя норма выработки, %

Месячная зарплата, грн.

I

90–94.8

3

92,53

304,3333333

II

94.8–99.6

4

97,55

342,75

III

99,6–104,4

11

102,1

363,4545455

IV

104,4–109,2

10

106,59

390,4

V

109,2–114

2

112

413

Всего:

30

102,69

367,07

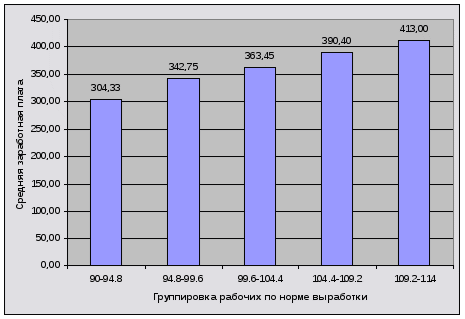
Построим гистограмму распределения (см. рисунок 1).

Рисунок 1 – Гистограмма распределения

Вывод: результаты группировки представлены в таблице 3, они свидетельствуют о том, что с увеличением выработки средняя месячная заработная плата увеличивается, то есть между нормой выработки рабочего и месячной заработной платой существует прямая зависимость. Данные по каждое группе представлены в таблице 3.

Задача 2.08

Имеются данные по трем заводам, вырабатывающим одноименную продукцию «КС1» (таблица 4).

Таблица 4

Завод

2002 год

2003 год

Затраты времени на единицу продукции, ч.

Изготовлено продукции, тыс. шт.

Затраты времени на единицу продукции, ч.

Затраты времени на всю продукцию, ч.

1

2,0

2,0

1,8

3960

2

2,5

5,0

2,3

11500

3

2,2

3,0

2,0

6400

Исчислите средние данные времени на всю продукцию по трем заводам в 2002 и 2003 гг. Укажите какие виды средних необходимо применить. Сделайте выводы.

Решение

Согласно условия, имеем:

X_i - iй вариант значения усредняемого признака – времени на изготовление продукции по двум годам (дано для 2002 и 2003 гг.),

f_i - частота iго варианта – изготовлено продукции шт. (дано для 2002 г.),

M_i - произведения значения признака и частоты – общие затраты времени на всю продукцию (дано для 2003 г.).

1. Рассчитаем среднюю затраты времени в 2002 г., используя формулу средней арифметической взвешенной (так как располагаем данными о значениях и частотах):

,

ч

2. Рассчитаем среднюю затраты времени в 2003 году, используя формулу средней гармонической взвешенной (так как располагаем данными о значениях, не располагаем данными о частотах, но имеем произведения значений и частот):

,

ч

3. Вывод: средние затраты времени в 2002 г. составили 2,31 ч. (рассчитано по формуле средней арифметической взвешенной, так как располагаем данными о значениях и частотах), в 2003 г. – 1,107 ч. (рассчитано по формуле средней гармонической взвешенной, так как располагаем данными о значениях и произведения значений и частот). Средняя время на изготовление продукции в 2002 г. больше на 1,203 ч., чем в 2003 г.

Задача 3.11

Распределение 260 металлорежущих станков на заводе характеризуется данными, представленными в таблице 5. Вычислите:

1. Средний срок службы станка;

2. Моду и медиану;

3. Среднее линейное отклонение;

4. Дисперсию и среднее квадратичное отклонение;

5. Коэффициент вариации;

Решение

Таблица 5

Срок службы, лет

до 4

4–8

8–12

12–16

свыше 16

Итого

Количество станков

50

90

40

50

30

260

Способ моментов основан на применении математических свойств средней арифметической взвешенной и позволяет значительно упростить технику вычисления. Расчет производится по формуле

,

где - момент первого порядка,

i – величина интервала (шаг),

A – постоянная величина, на которую уменьшаются все значения признака. В вариационных рядах с равными интервалами в качестве такой величины принимается вариант ряда, с наибольшей частотой.

Построим рабочую таблицу (см. таблицу 6).

Имеем

i=4, A=6 (при f max=90)

Таблица 6

Срок службы лет

количество станков

Середина интервала, X

до 4

50

2

-4

-1

-50

50

4–8

90

6

0

0

0

0

8–12

40

10

4

1

40

40

12–16

50

14

8

2

100

200

свыше 16

30

18

12

3

90

270

Итого:

260

20

180

560

Определим момент первого порядка

Определим момент второго порядка

Тогда имеем средняя продолжительность работы станка:

лет

Определим моду:

==9,78 лет.

Определим медиану:

==12,77 лет

Определим среднее линейное отклонение

=

Дисперсия определим по формуле:

Среднее квадратическое отклонение определим по формуле:

Коэффициент вариации:

Так как коэффициент вариации больше 33%, значит ряд не устойчивый (совокупность не однородная).

Ответ: средняя длительность работы станка 8,768 лет; дисперсия – 26,802, среднее квадратическое отклонение – 5,177; коэффициент вариации -59%;

Задача 4.12

Имеются данные о производстве продукции промышленного предприятия за 1994–1999 гг. смотреть таблицу 7

Таблица 7

Год

1994

1995

1996

1997

1998

1999

Произведено млн. грн.

8,0

8,4

8,9

9,5

10,1

10,8

Исчислите аналитические показатели ряда динамики продукции предприятия за 1994–1999 гг. абсолютное значение одного процента прироста, а также средние обобщающие показатели ряда динамики.

Решение

1) Абсолютный прирост базисный определяется по формуле:

,

где – уровни iго и базисного годов соответственно;

Абсолютный прирост цепной (по годам) определяется по формуле:

,

где – уровень предыдущего года;

Темп роста базисный определяется по формуле:

,

Темп роста цепной (по годам) определяется по формуле:

Темп прироста базисный определяется по формуле:

Темп прироста цепной (по годам) определяется по формуле:

Абсолютное содержание одного процента прироста определяется по формуле:

Рассчитаем по перечисленные величины и составим рабочую таблицу (см. таблица 8).

Таблица 8

Год

1994

1995

1996

1997

1998

1999

Произведено млн. грн.

8

8,4

8,9

9,5

10,1

10,8

Абсолютный прирост базисный

-

0,4

0,9

1,5

2,1

2,8

Абсолютный прирост цепной (по годам)

-

0,4

0,5

0,6

0,6

0,7

Темп роста базисный

-

105,00%

111,25%

118,75%

126,25%

135,00%

Темп роста цепной (по годам)

-

105,00%

105,95%

106,74%

106,32%

106,93%

Темп прироста базисный

-

5,00%

11,25%

18,75%

26,25%

35,00%

Темп прироста цепной (по годам)

-

5,00%

5,95%

6,74%

6,32%

6,93%

Абсолютное содержание 1го%-та прироста

-

0,08

0,084

0,089

0,095

0,101

Изобразим исходные данные графически (см. рисунок 2)

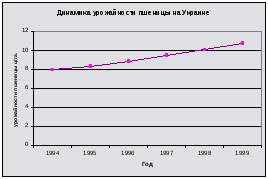
Рисунок 2 – Динамика производства продукции на предприятии с 1994 по 1999 год

Вывод: график показывает, что производство продукции на предприятии с 1994 г. по 1999 г. наблюдалась тенденция увеличения производства.

Задача 5.13

По городской телефонной сети из 1000 абонентов в порядке механической выборки произвели 100 наблюдений и установили, что средняя продолжительность телефонного разговора составляет 4 мин. При среднем квадратичном отклонении 2 мин.

Определите:

1. предельную ошибку репрезентативности (с вероятностью 0,954)

2. вероятность того, что предельная ошибка репрезантивности не превысила 0,3 мин.

Решение

1. Средняя ошибка среднего длительность звонка в выборке (выборочной средней)

Предельная ошибка репрезентивности с вероятностью 0,954 (гарантийный коэффициент) составит

2. Определим вероятность того, что предельная ошибка репрезантивности не превысила 0,3 мин.

Необходимая численность выборки при вероятности 0,954 (гарантийный коэффициент) определяется следующим образом:

.

Проверка. предельная ошибка длительности телефонного звонка составляет

чел.

Предельная ошибка выборочной средней при вероятности 0,954 ()

мин. не превышает заданной ошибки 0,3 мин.

Задача 6.16

Имеются данные о продаже товаров таблица 10

Таблица 10

Товарные группы

Продано товара в 2002 году млн. грн.

Индексы количества товаров в 2003 г. По сравнению с 2002 г.

Ткани шерстяные

45

0,97

Трикотажные изделия

54

1,12

Обувь

34

1,25

Вычислите общий индекс физического объема товарооборота в 2003 г. По сравнению с 2002 г.

Используя взаимосвязь индексов, определите, насколько процентов в среднем изменилась цена на проданные товары, если известно, что товарооборот в фактических ценах вырос на 10%

Товарные группы

Продано товара в 2002 году млн. грн.

Индексы количества товаров в 2003 г. По сравнению с 2002 г.

Ткани шерстяные

45

43,65

Трикотажные изделия

54

60,48

Обувь

34

42,5

Решение

1) Общий индекс физического объема товарооборота в 2003 г. по сравнению с 2002 г.

Общий индекс физического объема товарооборота вычисляется по формуле:

,

, тогда

=1,112 (111,2%)

Вывод: индекс физического объема товарооборота в 2003 г. по сравнению с 2002 г. в отчетном периоде увеличился на 11,2%.

2) Используя взаимосвязь индексов, определите, насколько процентов в среднем изменилась цена на проданные товары, если известно, что товарооборот в фактических ценах вырос на 10%.

Общий индекс цен вычисляется по формуле:

,

– изменение товарооборота в фактических ценах.

Вывод: при увеличении товарооборота на 10% проявляется тенденция снижения индекса цен на 9,1%

Список использованной литературы

1. Практикум по курсу «Статистика» для студентов всех специальностей. Часть 1 /Сост.: Акимова Е.В., Маркевич О.В. – Краматорск, ДГМА, 2002 – 59 с.

2. Практикум по курсу «Статистика» для студентов всех специальностей. Часть 2 /Сост.: Акимова Е.В., Маркевич О.В. – Краматорск, ДГМА, 2002 – 54 с.

3. Теория статистики: Учебник /Под ред. проф. Р.А. Шмойловой. – 3-е изд., перераб. – М.:

Финансы и статистика, 2002. – 560 с.: ил.

4. Практикум по теории статистики: Учеб. пособие /Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2003. – 416 с.: ил.