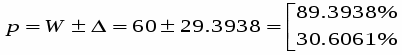
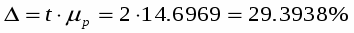
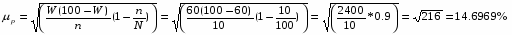
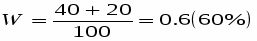
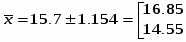
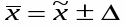
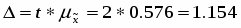
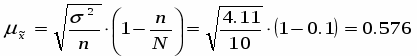
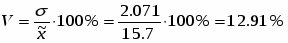
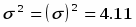
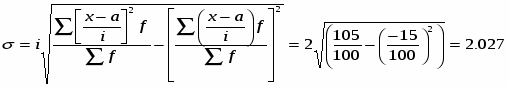
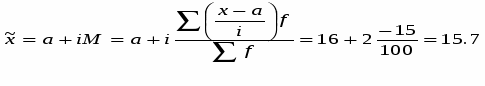
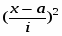
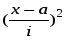
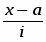
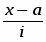
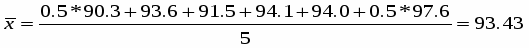
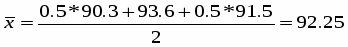
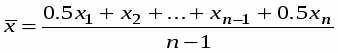ЗАДАЧА 1

Маємо наступні дані про залишки напівфабрикатів в цеху підприємства:

Дата

Кількість, тис. грн.

1 липня

90,3

1 серпня

93,6

1 вересня

91,5

1 жовтня

94,1

1 листопада

94,0

1 грудня

97,6

1 січня наступного року

100,2

Обчисліть розміри середніх залишків напівфабрикатів:

за ІІІ квартал

за І квартал

за ІІ півріччя

Поясніть відмінність розрахованих середніх

Рішення

В даному завданні ми маємо моментний ряд, а не періодичний, тому метод обчислення середньої відрізняється від методів, що були використані в задачах №3 та №4

Для вирішення завдання скористуємося хронологічною середньою, тому що моментів більше ніж 2 та інтервали між цими моментами однакові.

,

Залишки за ІІІ квартал:

Залишки за І квартал:

Так як в перший квартал входить лише 1 місяць – січень наступного року, то залишки будуть рівні – 100,2 тис. грн.

Залишки за ІІ півріччя

ЗАДАЧА 2

Під час вивчення урожайності зернових у господарствах АПК регіону проведено 5% вибіркове обстеження 100 га засіяної площі відібраних у випадковому порядку, в результаті якого отримали наступні дані(вибірка без повторна):

Урожайність, ц з га

Засіяна площа, га

До 13

10

13-15

25

15-17

40

17-19

20

Більше 19

5

Разом

100

Використавши наведені дані, обчислити:

середню урожайність зернових з 1 га

дисперсію і середнє квадратичне відхилення

коефіцієнт варіації

з ймовірністю 0,997 граничну похибку вибіркової середньої і можливі межі, в яких очікується середня урожайність у регіоні.

з ймовірністю 0,997 граничну похибку вибіркової долі і межі питомої ваги засіяних площ регіону з урожайністю від 15 до 19 ц з 1 га.

Рішення

Урожайність, ц з га

Засіяна площа. f

Середній інтервал, х

x-a

(a=16)

(i =2)

*f

*f

11-13

10

12

-4

-2

-20

4

40

13-15

25

14

-2

-1

-25

1

25

15-17

40

16

0

0

0

0

0

17-19

20

18

2

1

20

1

20

19-21

5

20

4

2

10

4

20

РАЗОМ

100

Х

Х

Х

-15

Х

105

Переводимо інтервальний ряд у дискретний для цього знаходимо середину. Оскільки інтервали рівновеликі розміри відкритих інтервалів приймаємо рівним іншим. Використовуючи підсумкову строку таблиці, А також значення a та i розраховуємо середню урожайність з 1 га.

Розраховуємо ст. похибку у виборці для середньої величини за умов без повторного відбору.

Розраховуємо граничну похибку для середньої величини.

Записуємо границі середньої урожайності.

З імовірністю 90% ми можемо стверджувати, що середня урожайність буде не нижче 14,55 ц з га і не вище 16,85.

Розраховуємо долю питомої ваги засіяних площ з урожайністю від 15 до 19 деталей

Розраховуємо граничну похибку вибіркової частини питомої ваги засіяних площ за умов безповторного відбору

з імовірністю 0,997 розраховуємо граничну похибку для частки ознаки

Доля питомої ваги засіяних площ з урожайністю від 15 до 19 деталей буде:

Таким чином, з імовірністю 99,7% ми можемо стверджувати, що питома вага засіяних площ з урожайністю від 15 до 19 га буде знаходитися в межах від 89,3938% до 30,6061%.