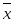
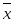
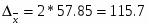
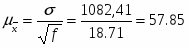
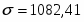
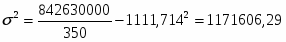
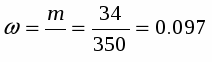
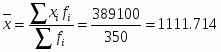
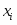
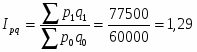
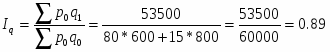
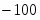
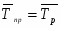
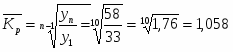
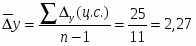
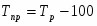
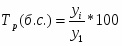
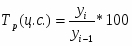
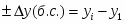
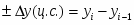
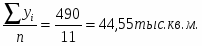
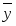
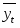
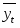
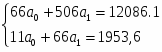
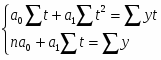
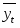
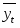
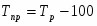
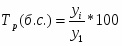
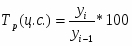
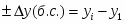
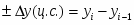
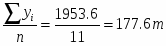
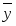
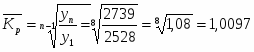
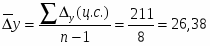
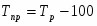
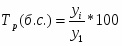
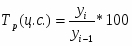
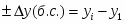
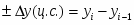Задача 1

Среднегодовая численность населения области выглядит следующим образом:

Год

Среднегодовая численность населения, тыс.чел.

1992

2528,0

1993

2655,0

1994

2689,0

1995

2722,0

1996

2747,4

1997

2747,7

1998

2750,5

1999

2747,9

2000

2739,0

Рассчитать абсолютные (цепные и базисные) и средние показатели динамики.

Решение

1. Требуемые показатели рассчитываются по формулам:

• Абсолютный прирост:

• Темп роста

• Темп прироста:

Полученные данные представим в таблице:

Год

Среднегодовая численность населения, тыс. чел.

Абсолютный прирост, млн. руб.

Темпы роста, %

Темпы прироста, %

к баз.

к отч.

к баз.

к отч.

к баз.

к отч.

1992

2528,0

0

-

100

-

0

-

1993

2655,0

127

127

105,0

105,0

5

5

1994

2689,0

161

34

106,4

101,3

6,4

1,3

1995

2722,0

194

33

107,7

101,2

7,7

1,2

1996

2747,4

219,4

25,4

108,7

100,9

8,7

0,9

1997

2747,7

219,7

0,3

108,7

100

8,7

0

1998

2750,5

222,5

2,8

108,8

100,1

8,8

0,1

1999

2747,9

219,9

-2,6

108,7

99,9

8,7

-0,1

2000

2739,0

211

-8,9

108,3

99,7

8,3

-0,3

Среднегодовой абсолютный прирост определим по формуле:

тыс. чел.

Среднегодовые темпы роста и прироста:

или 100,97%

=100,97-100 = 0,97%,

то есть ежегодно уровни ряда возрастали в среднем на 0,97%.

Задача 2

По одному из предприятий региона имеются следующие данные об объеме производства макаронных изделий:

Год

Объем производства, т.

1990

138,4

1991

155,4

1992

165,4

1993

168,1

1994

173,9

1995

178,1

1996

184,2

1997

189,7

1998

190,5

1999

200,2

2000

209,7

Определить:

1. среднегодовое производство макаронных изделий;

2. базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста производства макаронных изделий;

3. проверьте ряд динамики производства макаронных изделий на наличие тренда. Используя метод аналитического выравнивания, постройте уравнение прямой;

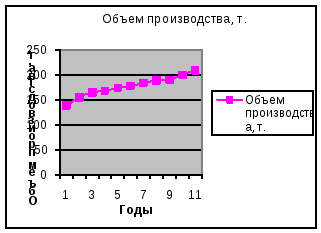
4. изобразите динамику производства макаронных изделий на графике.

Решение

1. Данный динамический ряд является интервальным, поэтому для определения среднегодового производства используем формулу арифметической простой:

=,

то есть в среднем в год производится 177,6 тонн макаронных изделий.

2. Базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста производства макаронных изделий рассчитываются по формулам:

• Абсолютный прирост:

• Темп роста:

• Темп прироста:

Полученные данные представим в таблице:

Год

Объем производства, т.

Абсолютный прирост, млн. руб.

Темпы роста, %

Темпы прироста, %

к баз.

к отч.

к баз.

к отч.

к баз.

к отч.

1990

138,4

0

-

100

-

0

-

1991

155,4

17

17

112,28

112,28

12,28

12,28

1992

165,4

27

10

119,51

106,44

19,51

6,44

1993

168,1

29,7

2,7

121,46

101,63

21,46

1,63

1994

173,9

35,5

5,8

125,65

103,45

25,65

3,45

1995

178,1

39,7

4,2

128,68

102,42

28,68

2,42

1996

184,2

45,8

6,1

133,09

103,43

33,09

3,43

1997

189,7

51,3

5,5

137,07

102,99

37,07

2,99

1998

190,5

52,1

0,8

137,64

100,42

37,64

0,42

1999

200,2

61,8

9,7

144,65

105,09

44,65

5,09

2000

209,7

71,3

9,5

151,52

104,75

51,52

4,75

3. Рассчитаем уравнение тренда ряда динамики.

Годы

Объем производства, т.

t

t²

yt

1990

138,4

1

1

138,4

-151,88

1991

155,4

2

4

310,8

-101,63

1992

165,4

3

9

196,2

-51,38

1993

168,1

4

16

672,4

-1,13

1994

173,9

5

25

869,5

49,12

1995

178,1

6

36

1068,6

99,37

1996

184,2

7

49

1289,4

149,62

1997

189,7

8

64

1517,6

199,87

1998

190,5

9

81

1714,5

250,12

1999

200,2

10

100

2002

300,37

2000

209,7

11

121

2306,7

350,62

Итого

1953,6

66

506

12086,1

1093,07

Для выравнивания ряда динамики по прямой следует получить уравнение: =a₀+a₁t.

Для расчета параметров а₀ и а₁ решается система нормальных уравнений:

Решив систему, получаем: a₀=-202,13, a₁=50,25.

Уравнение тренда примет вид: =-202,13+50,25t.

Ряд выровненных значений характеризует тенденцию стабильного увеличения выпуска продукции.

4. Изобразим динамику производства макаронных изделий на графике.

Задача 3

Имеются данные о вводе жилых домов по одной из строительных компаний:

Год

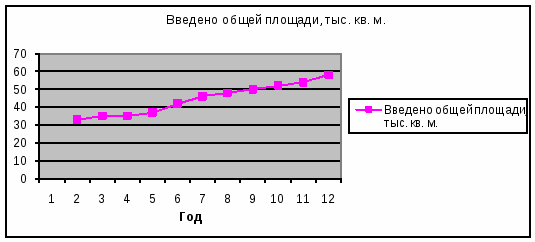
Введено общей площади, тыс. кв. м.

1990

33

1991

35

1992

35

1993

37

1994

42

1995

46

1996

48

1997

50

1998

52

1999

54

2000

58

Определить:

1. среднегодовой ввод жилых домов;

2. базисные, цепные и среднегодовых показатели абсолютного прироста, темпов роста и прироста ввода жилых домов.

3. на основе средних абсолютных приростов и темпов роста определить ожидаемый уровень ввода жилых домов в 2005 г.

4. изобразить динамику ввода жилых домов на графике.

Решение

1. Данный динамический ряд является интервальным, поэтому для определения среднегодового производства используем формулу арифметической простой:

=,

то есть в среднем в год вводится 44,55 тыс. кв. м

2. Требуемые показатели рассчитываются по формулам:

• Абсолютный прирост:

• Темп роста:

• Темп прироста:

Полученные данные представим в таблице:

Год

Введено общей площади, тыс. кв. м.

Абсолютный прирост, млн. руб.

Темпы роста, %

Темпы прироста, %

к баз.

к отч.

к баз.

к отч.

к баз.

к отч.

1990

33

0

-

100

-

0

-

1991

35

2

2

106,06

106,06

6,06

6,06

1992

35

2

0

106,06

100

6,06

0

1993

37

4

2

112,12

105,71

12,12

5,71

1994

42

9

5

127,27

113,51

27,27

13,51

1995

46

13

4

139,39

109,52

39,39

9,52

1996

48

15

2

145,45

104,35

45,45

4,35

1997

50

17

2

151,51

104,17

51,51

4,17

1998

52

19

2

157,58

104

57,58

4

1999

54

21

2

163,64

103,85

63,64

3,85

2000

58

25

4

175,76

107,41

75,76

7,41

Среднегодовой абсолютный прирост определим по формуле:

тыс. кв. м.

Среднегодовые темпы роста и прироста:

или 105,8%

=105,8-100 = 5,8%,

то есть ежегодно уровни ряда возрастали в среднем на 5,8%.

3. Если принять во внимание ввод жилых домов в 2000 и рассчитанный выше абсолютный прирост, то в 2005 году ввод жилых домов составит приблизительно 69,35 тыс. кв. м. (58+2,27*5).

4. Изобразим динамику ввода жилых домов на графике:

Задача 4

Имеются данные о ценах и количестве проданных товаров:

Вид товара

Единица измерения

Цена за единицу, руб.

Реализовано, тыс. ед.

Базисный период

Отчетный период

Базисный период

Отчетный период

Мясо

кг

80

110

600

500

Молоко

л

15

25

800

900

Определить:

1. общий индекс цен;

2. общий индекс физического объема товарооборота;

3. общий индекс товарооборота.

Решение

1. Общий индекс цен определим по формуле:

I_p=или 145%.

Следовательно, цены увеличились в среднем на 45%.

2. Общий индекс физического объема оборота рассчитаем по формуле:

или 89%.

Следовательно, физическая масса продажи снизилась на 11%.

3. Общий индекс оборота в действующих ценах:

или129%.

Взаимосвязь: 1,45*0,89=1,29

Задача 5

В коммерческом банке в порядке собственно-случайной выборки обследовано 5% кредитных договоров, в результате чего установлено:

Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб.

Число договоров с ссудозаемщиками

До 200

47

200-600

117

600-1400

105

1400-3000

47

3000 и более

34

ИТОГО

350

Определить:

1. по договорам, включенным в выборку:

а) средний размер выданного ссудозаемщиком кредита;

б) долю ссудозаемщиков, получивших кредит в размере более 3000 тыс. руб.

2. с вероятностью 0,954 пределы, в которых можно ожидать средний размер выданного ссудозаемщикам кредита и доли судозаемщиков, получивших кредит в размере более 3000 тыс. руб. в целом по отделению банка.

Решение

1. Закроем интервалы, определим центры интервалов, рассчитаем размер кредитов во всех договорах и занесем расчетные показатели в таблицу:

Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб.

Число договоров с ссудозаемщиками (f_i)

Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб.

Середина интервала

()

Размер кредитов во всех договорах, тыс. руб. (x_if_i)

x²f

До 200

47

0-200

100

4700

470000

200-600

117

200-600

400

46800

18720000

600-1400

105

600-1400

1000

105000

105000000

1400-3000

47

1400-3000

2200

103400

227480000

3000 и более

34

3000-4600

3800

129200

490960000

ИТОГО

350

-

-

389100

842630000

а) для определения среднего размера выданного ссудозаемщиком кредита воспользуемся формулой средней арифметической взвешенной:

тыс. руб.

б) доля ссудозаемщиков, получивших кредит в размере более 3000 тыс. руб. равна:

или 9,7%.

2. Определим с вероятностью 0,954 пределы, в которых можно ожидать средний размер выданного ссудозаемщикам кредита и доли судозаемщиков, получивших кредит в размере более 3000 тыс. руб. в целом по отделению банка.

Дисперсия рассчитывается по формуле:

Средняя ошибка выборки составит:

t=2

тыс. руб.

Установим границы: 1111,714-115,7≤≤1111,714+115,7

996,014≤≤1227,414

Значит, на основании проведенного обследования с вероятностью 0,954 можно заключить, что средний размер выданного ссудозаемщикам кредита, получивших кредит в размере более 3000 тыс. руб., в целом по отделению банка лежит в пределах от 996,014 до 1227,414 тыс. руб.

Список использованной литературы

1. Теория статистики: Учебник / Р. А. Шмойлова, В. Г. Минашкин, Н. А. Садовникова, Е. Б. Шувалова; Под ред. Р. А. Шмойловой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – 656с.

2. Гусаров В.М. Статистика: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2001.

3. Октябрьский П. Я. Статистика: Учебник. – М.: ТК Велби, Изд-во Проспект, 2005. – 328 с.

4. Сборник задач по теории статистики: Учебное пособие/ Под ред.проф. В.В.Глинского и к.э.н., доц. Л.К.Серга. Изд.З-е.- М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.

5. Статистика: Учебное пособие/Харченко Л-П., Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г.Ионина. - Изд. 2-е, перераб. и доп. - М.: ИНФРА-М.2003.