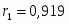
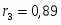
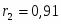
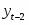
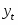
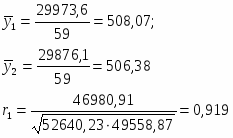
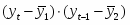
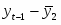
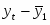
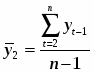
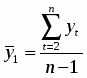
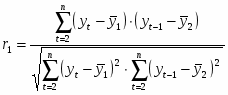
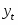
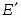
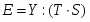
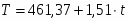
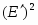
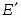
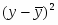
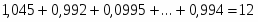
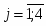
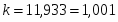
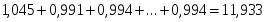
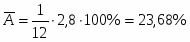
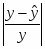
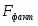
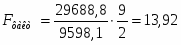
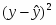
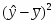
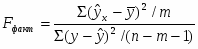
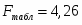
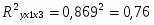
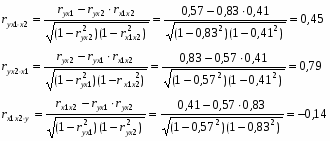
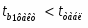
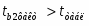
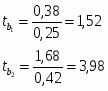
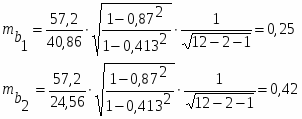
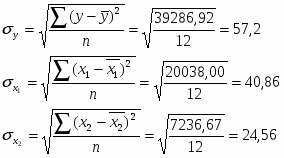
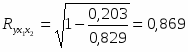
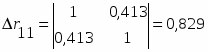
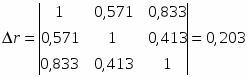
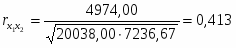
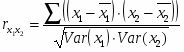
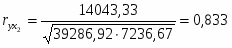
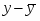
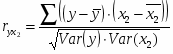
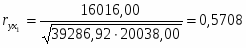
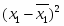
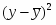
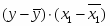
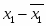
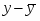
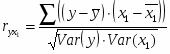
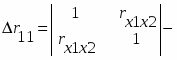
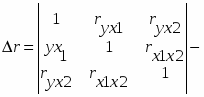
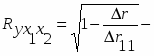
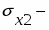
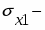
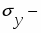
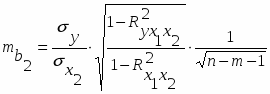
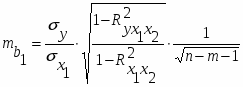
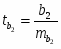
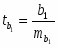
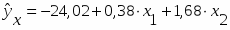
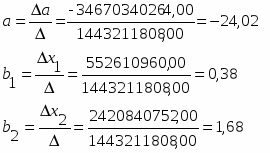
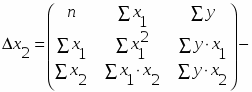
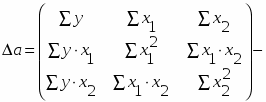
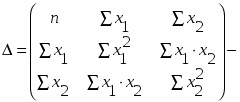
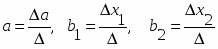
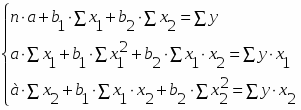
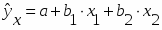
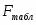
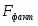
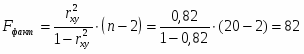
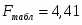
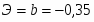
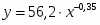
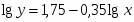
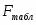
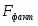
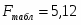
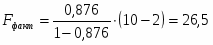
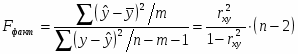
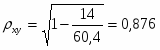
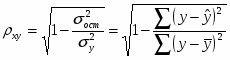
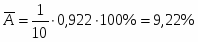
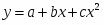
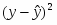
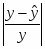
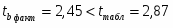
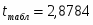
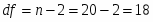
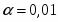
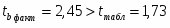
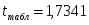
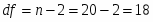
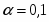
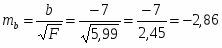
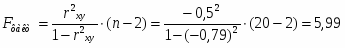
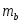
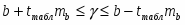
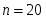
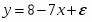Задача 1

Пусть имеется следующая модель регрессии, характеризующая зависимость x от y:

.

Известно также, что, .

Задание

1. Постройте доверительный интервал для коэффициента регрессии в этой модели:

   1. с вероятностью 90%;

   2. с вероятностью 99%.

2. Проанализируйте результаты, полученные в п.1, и поясните причины их различий.

Решение.

Формула для расчета доверительного интервала для коэффициента регрессии имеет вид:

где - случайная ошибка параметра линейной регрессии. Оценка значимости коэффициента регрессии проводится путем сопоставления его значения с величиной случайной ошибки.

где F – F-критерий Фишера и определяется из соотношения:

Тогда

При и числа степеней свободы табличное значение .

Сравнив его с расчетными значениями, получаем, что , из чего следует, что гипотезу о несущественности параметра b с вероятностью 90% (p = 1 – α) следует отклонить

Для коэффициента регрессии в примере 90 %-ые границы составят:

-7 + 1,7143 · (-2,86) ≤ b ≤ -7 - 1,7143 · (-2,86)

-11,9 ≤ b ≤ -2,04

При и числа степеней свободы табличное значение .

Сравнив его с расчетными значениями, получаем, что , из чего следует, что гипотезу о несущественности параметра b с вероятностью 99% (p = 1 – α) следует принять и признается статистическая незначимость параметра b.

Для коэффициента регрессии в примере 99 %-ые границы составят:

-7 + 2,8784 · (-2,86) ≤ b ≤ -7 – 2,8784 · (-2,86)

-15,23 ≤ b ≤ 1,232

Получили, что доверительный интервал для коэффициента корреляции с вероятностью 90% значительно меньше доверительного интервала с вероятностью 99%. Это объясняется тем, что при увеличении интервала вероятность попадания в него оцениваемого параметра растет и наоборот, с уменьшением интервала – вероятность снижается.

№

Производительность труда рабочих, тыс.руб., y

фактическая, y

расчетная,

1

12

10

0,167

4

0,16

2

8

10

0,250

4

12,96

3

13

13

0,000

0

1,96

4

15

14

0,067

1

11,56

5

16

15

0,063

1

19,36

6

11

12

0,091

1

0,36

7

12

13

0,083

1

0,16

8

9

10

0,111

1

6,76

9

11

10

0,091

1

0,36

10

9

9

0

0

6,76

Итого:

-

-

0,922

14

60,40

Ср. значение

11,6

-

-

-

-

Задача 2

Зависимость среднемесячной производительности труда от возраста рабочих характеризуется моделью . Ее использование привело к результатам, представленным в таблице:

№

Производительность труда рабочих, тыс.руб., y

фактическая

расчетная

1

12

10

2

8

10

3

13

13

4

15

14

5

16

15

6

11

12

7

12

13

8

9

10

9

11

10

10

9

9

Задание

Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.

Решение

Значение средней ошибки аппроксимации находится по формуле:

Рассчитанное значение средней ошибки аппроксимации говорит о предельном качестве модели, поскольку близко подходит к критическому пределу в 10%.

Индекс корреляции (для нелинейной регрессии):

Найденное значение индекса корреляции говорит о наличии близкой зависимости среднемесячной производительности труда от возраста рабочих.

F-критерий Фишера:

.

При уровне значимости α = 0,05, k₁ = 1 (m) и k₂ = 10 (n-m-1=10-1-1) степенях свободы табличное значение F-критерия Фишера .

=26,5 > =5,12, значит, H₀ – гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность. Вывод: показатели рассчитанных коэффициентов позволяют предложить отобразить зависимость среднемесячной производительности труда от возраста рабочих выбором более точной модели путем введения дополнительных переменных, либо изменением уравнения регрессии.

Задача 3

регрессия аппроксимация корреляция спрос

Зависимость спроса на товар K от его цены характеризуется по 20 наблюдениям уравнением: . Доля остаточной дисперсии в общей составила 18%.

Задание

1. Запишите данное уравнение в виде степенной функции.

2. Оцените эластичность спроса на товар в зависимости от его цены.

3. Определите индекс корреляции.

4. Оцените значимость уравнения регрессии через F-критерий Фишера. Сделайте выводы.

Решение.

1. Уравнение в виде степенной функции:

2. Эластичность степенной функции:

Фактором снижения спроса выступает его цена: с ростом цены на 1%, спрос снижается на 0,35%.

3. Индекс корреляции (для нелинейной регрессии):

Поскольку доля остаточной дисперсии в общей составила 18%, поэтому уравнение регрессии объясняется 82% дисперсии результативного признака, т. е. коэффициент детерминации равен R² = 0,82.

Индекс корреляции находится: Величина индекса корреляции достаточно близка к 1 и означает наличие достаточно тесной связи объема спроса от размера цены.

F –тест состоит в проверке гипотезы H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравнивается фактическое и критическое значение F-критерия Фишера. При уровне значимости α = 0,05, k₁ = 1 (m) и k₂ = 20 (n-m-1=20-1-1) степенях свободы табличное значение F-критерия Фишера :

.

> ,

то H₀ – гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.

Вывод: уравнение регрессии характеризует достаточно тесную зависимость спроса на товар K от его цены. Причем, наблюдается обратная зависимость: с увеличением цены, спрос падает.

Задача 4

Изучение влияния стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 12 торговым предприятиям были получены данные, приведенные в таблице:

Номер предприятия

Валовой доход за год, млн.руб.

Среднегодовая стоимость, млн.руб.

основных фондов

оборотных средств

1

203

118

105

2

63

28

56

3

45

17

54

4

113

50

63

5

121

56

28

6

88

102

50

7

110

116

54

8

56

124

42

9

80

114

36

10

237

154

106

11

160

115

88

12

75

98

46

Задание

1. Постройте линейное уравнение множественной регрессии и поясните экономический смысл его параметров. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия.

2. Рассчитайте средние коэффициенты эластичности.

3. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделайте выводы о силе связи результата и факторов.

4. Дайте оценку полученного уравнения на основе общего F-критерия Фишера.

5. Оцените качество уравнения через среднюю ошибку аппроксимации.

6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

7. Оцените полученные результаты, выводы оформите в аналитической записке.

Решение.

Построение линейной множественной регрессии сводится к оценке ее параметров – а, b₁ и b_2. Для расчета параметров а, b₁ и b₂ уравнения регрессии решаем систему нормальных уравнений относительно а, b₁ и b₂:

По исходным данным произведем расчет предварительных параметров (табл. 4.1)

Таблица 4.1

№

У

Х₁

Х₂

Х₁²

Х₂²

Х₁·Х₂

У·Х₁

У·Х₂

ŷ

1

203

118

105

13924,00

11025,00

12390,00

23954,00

21315,00

197,29

2

63

28

56

784,00

3136,00

1568,00

1764,00

3528,00

80,63

3

45

17

54

289,00

2916,00

918,00

765,00

2430,00

73,07

4

113

50

63

2500,00

3969,00

3150,00

5650,00

7119,00

100,80

5

121

56

28

3136,00

784,00

1568,00

6776,00

3388,00

44,39

6

88

102

50

10404,00

2500,00

5100,00

8976,00

4400,00

98,90

7

110

116

54

13456,00

2916,00

6264,00

12760,00

5940,00

110,97

8

56

124

42

15376,00

1764,00

5208,00

6944,00

2352,00

93,91

9

80

114

36

12996,00

1296,00

4104,00

9120,00

2880,00

80,01

10

237

154

106

23716,00

11236,00

16324,00

36498,00

25122,00

212,75

11

160

115

88

13225,00

7744,00

10120,00

18400,00

14080,00

167,62

12

75

98

46

9604,00

2116,00

4508,00

7350,00

3450,00

90,66

Итого:

1351,00

1092,0

728,0

119410,0

51402,0

71222,0

138957,0

96004,0

1351,00

Систему линейных уравнений удобно решать методом Крамера (метод определителей):

- частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

частный определитель параметра а.

частный определитель параметра х₁.

частный определитель параметра х₂.

Теперь произведем расчет коэффициентов множественной регрессии:

Аналогичные результаты можно получить с помощью автоматической процедуры нахождения параметров «Анализ данных» → «Регрессия» MS Excel уравнения множественной регрессии:

Окончательно уравнение множественной регрессии, связывающее валовой доход за год (у) со средней стоимостью основных фондов (х₁) и со средней стоимостью оборотных средств (х₂) имеет вид:

Анализ данного уравнения позволяет сделать выводы – с увеличением среднегодовой стоимости основных фондов на 1 млн. руб. размер валового дохода возрастет в среднем на 380 тыс. руб., при том же стоимости оборотных средств. Увеличение среднегодовой стоимости оборотных средств на 1 млн. руб. при той же стоимости основных фондов предполагает дополнительное увеличение валового дохода за год на 1,68 млн. руб.

Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента и доверительные интервалы для каждого из них. Выдвигается гипотеза H₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки по формулам:

и .

Где случайные ошибки параметров линейной регрессии определяются следующим образом:

;

средняя квадратическая ошибка i-го коэффициента регрессии (стандартная ошибка i-го коэффициента регрессии);

среднеквадратичное отклонение величины у;

среднеквадратичное отклонение величины х₁;

среднеквадратичное отклонение величины х₂;

совокупный коэффициент множественной корреляции;

определитель матрицы парных коэффициентов корреляции;

определитель матрицы межфакторной корреляции. Как видно, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым их факторов, но и от межфакторной корреляции. Парный коэффициент корреляции между у и х₁ рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.2

Таблица 4.2

№

У

Х₁

1

203,0

118,0

90,4

27,0

2441,25

8175,17

729,00

2

63,0

28,0

-49,6

-63,0

3123,75

2458,51

3969,00

3

45,0

17,0

-67,6

-74,0

5001,17

4567,51

5476,00

4

113,0

50,0

0,4

-41,0

-17,08

0,17

1681,00

5

121,0

56,0

8,4

-35,0

-294,58

70,84

1225,00

6

88,0

102,0

-24,6

11,0

-270,42

604,34

121,00

7

110,0

116,0

-2,6

25,0

-64,58

6,67

625,00

8

56,0

124,0

-56,6

33,0

-1867,25

3201,67

1089,00

9

80,0

114,0

-32,6

23,0

-749,42

1061,67

529,00

10

237,0

154,0

124,4

63,0

7838,25

15479,51

3969,00

11

160,0

115,0

47,4

24,0

1138,00

2248,34

576,00

12

75,0

98,0

-37,6

7,0

-263,08

1412,51

49,00

Итого

1351,00

1092,00

16016,00

39286,92

20038,00

Среднее значение

112,6

91,0

Тогда коэффициент корреляции между у и х₁ составит:

Парный коэффициент корреляции между у и х₂ рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.3

Таблица 4.3

№

У

Х₂

1

203,0

105,0

90,4

44,3

4008,47

8175,17

1965,44

2

63,0

56,0

-49,6

-4,7

231,39

2458,51

21,78

3

45,0

54,0

-67,6

-6,7

450,56

4567,51

44,44

4

113,0

63,0

0,4

2,3

0,97

0,17

5,44

5

121,0

28,0

8,4

-32,7

-274,94

70,84

1067,11

6

88,0

50,0

-24,6

-10,7

262,22

604,34

113,78

7

110,0

54,0

-2,6

-6,7

17,22

6,67

44,44

8

56,0

42,0

-56,6

-18,7

1056,22

3201,67

348,44

9

80,0

36,0

-32,6

-24,7

803,72

1061,67

608,44

10

237,0

106,0

124,4

45,3

5640,22

15479,51

2055,11

11

160,0

88,0

47,4

27,3

1296,06

2248,34

747,11

12

75,0

46,0

-37,6

-14,7

551,22

1412,51

215,11

Итого

1351,00

728,00

 

 

14043,33

39286,92

7236,67

Среднее значение

112,6

60,7

 

 

 

 

 

Тогда коэффициент корреляции между у и х₂ составит:

Парный коэффициент корреляции между х₁ и х₂ рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.4

Таблица 4.4

№

х₁

х₂

1

118,0

105,0

27,0

44,3

1197,00

729,00

1965,44

2

28,0

56,0

-63,0

-4,7

294,00

3969,00

21,78

3

17,0

54,0

-74,0

-6,7

493,33

5476,00

44,44

4

50,0

63,0

-41,0

2,3

-95,67

1681,00

5,44

5

56,0

28,0

-35,0

-32,7

1143,33

1225,00

1067,11

6

102,0

50,0

11,0

-10,7

-117,33

121,00

113,78

7

116,0

54,0

25,0

-6,7

-166,67

625,00

44,44

8

124,0

42,0

33,0

-18,7

-616,00

1089,00

348,44

9

114,0

36,0

23,0

-24,7

-567,33

529,00

608,44

10

154,0

106,0

63,0

45,3

2856,00

3969,00

2055,11

11

115,0

88,0

24,0

27,3

656,00

576,00

747,11

12

98,0

46,0

7,0

-14,7

-102,67

49,00

215,11

Итого

1092,00

728,00

4974,00

20038,00

7236,67

Средне значение

91,0

60,7

Тогда коэффициент корреляции между х₁ и х₂ составит:

При трех переменных для двухфакторного уравнения регрессии рассчитаем определители матрицы парной корреляции и межфакторной корреляции:

;

Тогда совокупный коэффициент множественной корреляции составит:

По данным из табл. 2, 3 рассчитаем теперь среднее квадратическое отклонение величин у, х₁ и х₂ по формулам:

Рассчитаем теперь средние квадратические ошибки коэффициентов регрессии b₁ и b₂

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значений:

При уровне значимости α = 0,05, df = 11 (n-m-1=12-2-1) степенях свободы табличное значение t-критерия Стьюдента 2,26.

Сравнив его с расчетными значениями, получаем, что , из чего следует, что гипотезу о несущественности параметра b₂ с вероятностью 95% (p = 1 – α) следует отклонить. А вот из чего следует, что гипотезу о несущественности параметра b₁ с вероятностью 95% (p = 1 – α) следует принять и признается статистическая незначимость параметра b₁.

2. Для характеристики относительной силы влияния х₁ и х₂ на у используя коэффициенты регрессии можно рассчитать средние коэффициенты эластичности. Как правило, их рассчитывают для средних значений факторов и результатов.

С увеличением среднегодовой стоимости основных фондов (х₁) на 1% от его среднего уровня, средний объем валового дохода за год увеличится на 0,37% от своего среднего уровня; при повышении среднегодовой стоимости оборотных средств на 1% - увеличится на 0,53% от своего среднего уровня. Очевидно, что сила влияния средней стоимости оборотных средств (х₂) на валовой доход (у) оказалась сильнее, чем сила влияния средней стоимости основных фондов (х₁).

Рассчитаем линейные коэффициенты частной корреляции

Расчёт линейного коэффициента множественной корреляции и коэффициентов парной корреляции выполнен в п.1 Коэффициент множественной детерминации рассчитывается как квадрат коэффициента множественной корреляции:

Зависимость у от х₁ и х₂ характеризуется как тесная, в которой 76% вариации валового дохода определяются вариацией учтенных в модели факторов: среднегодовой стоимости основных фондов и среднегодовой стоимости оборотных средств. Прочие факторы, не включенные в модель, составляют соответственно 14% от общей вариации у.

4. F –тест Фишера состоит в проверке гипотезы H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравнивается фактическое и критическое значение F-критерия Фишера. При уровне значимости α = 0,05, k₁ = 2 (m) и k₂ = 9 (n-m-1=12-2-1) степенях свободы табличное значение F-критерия Фишера:

Таблица 4.5

№

у

ŷ

1

203

197,29

7174,61

32,65

2

63

80,63

1020,85

310,91

3

45

73,07

1561,63

787,69

4

113

100,80

138,89

148,88

5

121

44,39

4650,78

5869,60

6

88

98,90

187,15

118,88

7

110

110,97

2,59

0,95

8

56

93,91

348,78

1437,00

9

80

80,01

1060,74

0,00

10

237

212,75

10033,02

588,14

11

160

167,62

3029,24

58,09

12

75

90,66

480,55

245,29

Сумма

1351,00

29688,8

9598,1

Тогда

> , значит, H₀ – гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.

Значение средней ошибки аппроксимации найдем по формуле:

Таблица.4.6 Расчет ошибки аппроксимации

№

у

ŷ

1

203,0

197,29

0,03

2

63,0

80,63

0,28

3

45,0

73,07

0,62

4

113,0

100,80

0,11

5

121,0

44,39

0,63

6

88,0

98,90

0,12

7

110,0

110,97

0,01

8

56,0

93,91

0,68

9

80,0

80,01

0,00

10

237,0

212,75

0,10

11

160,0

167,62

0,05

12

75,0

90,66

0,21

13

1351,0

1351,0

2,8

14

203,0

197,29

0,03

Сумма

63,0

80,63

0,28

Ошибка аппроксимации показала очень сильное отличие фактического значения результативного признака от теоретического, рассчитанного по множественному уравнению регрессии, что свидетельствует о плохом выборе уравнения регрессии.

Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

Задача 5

Имеются данные об объемах продаж в перерабатывающей промышленности и торговле США в течение 5 лет в сопоставимых ценах в млрд. долл.

Месяц

1 год

2 год

3 год

4 год

5 год

Январь

472,5

477,9

510,9

541,0

578,2

Февраль

482,1

467,5

484,7

512,3

539,4

Март

489,5

470,9

486,6

512,6

545,3

Апрель

493,6

469,1

488,4

511,5

551,9

Май

488,0

478,1

489,5

511,9

549,7

Июнь

490,6

480,6

486,6

513,9

550,1

Июль

492,5

479,3

491,8

520,0

554,0

Август

488,1

484,2

495,2

515,9

550,0

Сентябрь

493,1

484,9

491,8

524,2

565,6

Октябрь

484,5

485,6

496,1

527,1

564,7

Ноябрь

483,0

486,1

498,8

529,8

566,9

Декабрь

476,9

484,7

501,5

534,9

572,7

Задание

Рассчитайте трендовую и сезонную компоненты. Постройте мультипликативную модель этого ряда. Найдите наиболее целесообразный вариант построения уравнения авторегрессии через расчет коэффициентов автокорреляции первого, второго и третьего порядка. Охарактеризуйте структуру этого ряда.

Решение

1. Расчет оценок сезонной компоненты в мультипликативной модели

Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый месяц (по всем годам) оценки сезонной компоненты S_j. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле, т.е. двенадцати, так как в нашем случае число периодов одного цикла (год) равно 12 месяцам. Для данной модели имеем:

.

Определим корректирующий коэффициент:

.

Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:

,

где .

Проверим условие равенства двенадцати суммы значений сезонной компоненты:

.

Таким образом, получены следующие значения сезонной компоненты:

Элиминируем влияние сезонной компоненты, разделив значение каждого уровня исходного временного ряда на соответствующие значения сезонной компоненты. Получим T∙E=Y/S, значения, которые содержат только тенденцию и случайную компоненту.

Таблица 5.3 Расчет выравненных значений Т и ошибок Е в мультипликативной модели

t

y

S

y/S

T

T·S

E

1

472,5

1,045

452,024

462,884

483,852

1223,600

0,977

-11,352

128,866

2

482,1

0,992

486,039

464,396

460,632

644,144

1,047

21,468

460,863

3

489,5

0,995

492,032

465,908

463,510

323,280

1,056

25,990

675,460

4

493,6

0,994

496,428

467,419

464,757

192,654

1,062

28,843

831,923

5

488

0,996

490,190

468,931

466,836

379,470

1,045

21,164

447,915

6

490,6

0,993

494,071

470,443

467,138

284,934

1,050

23,462

550,462

7

492,5

1,000

492,362

471,955

472,087

224,400

1,043

20,413

416,700

8

488,1

0,997

489,587

473,466

472,028

375,584

1,034

16,072

258,315

9

493,1

1,000

493,166

474,978

474,915

206,784

1,038

18,185

330,712

10

484,5

0,997

485,935

476,490

475,083

528,080

1,020

9,417

88,688

11

483

0,997

484,563

478,001

476,459

599,270

1,014

6,541

42,783

12

476,9

0,994

479,676

479,513

476,738

935,136

1,000

0,162

0,026

13

477,9

1,045

457,190

481,025

502,814

874,976

0,950

-24,914

620,722

14

467,5

0,992

471,320

482,537

478,626

1598,400

0,977

-11,126

123,785

15

470,9

0,995

473,336

484,048

481,558

1338,096

0,978

-10,658

113,586

16

469,1

0,994

471,787

485,560

482,794

1473,024

0,972

-13,694

187,532

17

478,1

0,996

480,246

487,072

484,896

863,184

0,986

-6,796

46,180

18

480,6

0,993

484,000

488,584

485,151

722,534

0,991

-4,551

20,714

19

479,3

1,000

479,166

490,095

490,233

794,112

0,978

-10,933

119,520

20

484,2

0,997

485,676

491,607

490,113

541,958

0,988

-5,913

34,968

21

484,9

1,000

484,965

493,119

493,053

509,856

0,983

-8,153

66,467

22

485,6

0,997

487,038

494,630

493,170

478,734

0,985

-7,570

57,300

23

486,1

0,997

487,674

496,142

494,541

457,104

0,983

-8,441

71,255

24

484,7

0,994

487,521

497,654

494,774

518,928

0,980

-10,074

101,480

25

510,9

1,045

488,760

499,166

521,777

11,696

0,979

-10,877

118,302

26

484,7

0,992

488,660

500,677

496,620

518,928

0,976

-11,920

142,075

27

486,6

0,995

489,117

502,189

499,605

435,974

0,974

-13,005

169,130

28

488,4

0,994

491,198

503,701

500,832

364,046

0,975

-12,432

154,543

29

489,5

0,996

491,697

505,212

502,955

323,280

0,973

-13,455

181,042

30

486,6

0,993

490,042

506,724

503,164

435,974

0,967

-16,564

274,382

31

491,8

1,000

491,662

508,236

508,378

245,862

0,967

-16,578

274,837

32

495,2

0,997

496,709

509,748

508,199

150,798

0,974

-12,999

168,971

33

491,8

1,000

491,866

511,259

511,191

245,862

0,962

-19,391

376,008

34

496,1

0,997

497,569

512,771

511,257

129,504

0,970

-15,157

229,726

35

498,8

0,997

500,415

514,283

512,623

75,342

0,973

-13,823

191,086

36

501,5

0,994

504,419

515,794

512,809

35,760

0,978

-11,309

127,902

37

541

1,045

517,556

517,306

540,739

1123,590

1,000

0,261

0,068

38

512,3

0,992

516,486

518,818

514,613

23,232

0,996

-2,313

5,351

39

512,6

0,995

515,251

520,330

517,652

26,214

0,990

-5,052

25,526

40

511,5

0,994

514,430

521,841

518,869

16,160

0,986

-7,369

54,300

41

511,9

0,996

514,197

523,353

521,015

19,536

0,983

-9,115

83,079

42

513,9

0,993

517,536

524,865

521,178

41,216

0,986

-7,278

52,965

43

520

1,000

519,854

526,376

526,524

156,750

0,988

-6,524

42,562

44

515,9

0,997

517,472

527,888

526,284

70,896

0,980

-10,384

107,836

45

524,2

1,000

524,270

529,400

529,329

279,558

0,990

-5,129

26,308

46

527,1

0,997

528,661

530,912

529,344

384,944

0,996

-2,244

5,035

47

529,8

0,997

531,515

532,423

530,705

498,182

0,998

-0,905

0,820

48

534,9

0,994

538,014

533,935

530,845

751,856

1,008

4,055

16,443

49

578,2

1,045

553,144

535,447

559,701

5001,318

1,033

18,499

342,198

50

539,4

0,992

543,807

536,959

532,607

1018,886

1,013

6,793

46,148

51

545,3

0,995

548,120

538,470

535,700

1430,352

1,018

9,600

92,168

52

551,9

0,994

555,062

539,982

536,906

1973,136

1,028

14,994

224,816

53

549,7

0,996

552,167

541,494

539,074

1782,528

1,020

10,626

112,904

54

550,1

0,993

553,992

543,005

539,191

1816,464

1,020

10,909

119,009

55

554

1,000

553,845

544,517

544,670

2164,110

1,017

9,330

87,055

56

550

0,997

551,676

546,029

544,370

1807,950

1,010

5,630

31,698

57

565,6

1,000

565,676

547,541

547,467

3377,934

1,033

18,133

328,793

58

564,7

0,997

566,373

549,052

547,431

3274,128

1,032

17,269

298,224

59

566,9

0,997

568,735

550,564

548,788

3530,736

1,033

18,112

328,060

60

572,7

0,994

576,034

552,076

548,881

4253,648

1,043

23,819

567,361

Итого

52661,016

60,006

1,751

11202,95

Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (T∙E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:

Таким образом, имеем линейный тренд:

.

Подставив в это уравнение значение t = 1, 2, …, 60, найдем уровни Т для каждого момента времени.

Найдем значения уровней ряда, полученные по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих месяцев.

Расчет ошибки в мультипликативной модели проводится по формуле:

.

Численные значения ошибок приведены в таблице

Для оценки качества построения мультипликативной модели можно использовать сумму квадратов абсолютных ошибок. Для данной мультипликативной модели сумма квадратов абсолютных ошибок равна 11202,95. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 52661,016, эта величина составляет 21,2%:

.

Следовательно, можно сказать, что мультипликативная модель объясняет 78,8% общей вариации уровней временного ряда объема продаж в перерабатывающей промышленности и торговле США за последние 60 месяцев. Мультипликативная модель построена.

При этом при расчете коэффициента автокорреляции первого порядка параметрами будут являться значения исходного ряда и значения ряда с отставанием на 1 .

;

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.

Таблица 5.4 Расчет коэффициента автокорреляции первого порядка

t

y

1

472,5

-

-

-

-

-

-

2

482,1

472,5

-25,9729

-33,8746

879,8204

674,5906

1147,4869

3

489,5

482,1

-18,5729

-24,2746

450,8488

344,9519

589,2551

4

493,6

489,5

-14,4729

-16,8746

244,2237

209,4643

284,7513

5

488

493,6

-20,0729

-12,7746

256,4226

402,9206

163,1898

6

490,6

488

-17,4729

-18,3746

321,0568

305,3016

337,6251

7

492,5

490,6

-15,5729

-15,7746

245,6556

242,5146

248,8373

8

488,1

492,5

-19,9729

-13,8746

277,1153

398,9160

192,5039

9

493,1

488,1

-14,9729

-18,2746

273,6231

224,1872

333,9601

10

484,5

493,1

-23,5729

-13,2746

312,9200

555,6807

176,2144

11

483

484,5

-25,0729

-21,8746

548,4587

628,6494

478,4971

12

476,9

483

-31,1729

-23,3746

728,6529

971,7485

546,3708

13

477,9

476,9

-30,1729

-29,4746

889,3329

910,4028

868,7506

14

467,5

477,9

-40,5729

-28,4746

1155,2956

1646,1587

810,8015

15

470,9

467,5

-37,1729

-38,8746

1445,0800

1381,8231

1511,2327

16

469,1

470,9

-38,9729

-35,4746

1382,5465

1518,8855

1258,4456

17

478,1

469,1

-29,9729

-37,2746

1117,2265

898,3736

1389,3940

18

480,6

478,1

-27,4729

-28,2746

776,7841

754,7592

799,4517

19

479,3

480,6

-28,7729

-25,7746

741,6088

827,8787

664,3288

20

484,2

479,3

-23,8729

-27,0746

646,3481

569,9145

733,0327

21

484,9

484,2

-23,1729

-22,1746

513,8488

536,9824

491,7118

22

485,6

484,9

-22,4729

-21,4746

482,5956

505,0304

461,1574

23

486,1

485,6

-21,9729

-20,7746

456,4773

482,8075

431,5830

24

484,7

486,1

-23,3729

-20,2746

473,8753

546,2916

411,0584

25

510,9

484,7

2,8271

-21,6746

-61,2766

7,9926

469,7873

26

484,7

510,9

-23,3729

4,5254

-105,7722

546,2916

20,4795

27

486,6

484,7

-21,4729

-21,6746

465,4156

461,0846

469,7873

28

488,4

486,6

-19,6729

-19,7746

389,0229

387,0223

391,0339

29

489,5

488,4

-18,5729

-17,9746

333,8397

344,9519

323,0854

30

486,6

489,5

-21,4729

-16,8746

362,3458

461,0846

284,7513

31

491,8

486,6

-16,2729

-19,7746

321,7893

264,8067

391,0339

32

495,2

491,8

-12,8729

-14,5746

187,6168

165,7111

212,4183

33

491,8

495,2

-16,2729

-11,1746

181,8426

264,8067

124,8712

34

496,1

491,8

-11,9729

-14,5746

174,4997

143,3499

212,4183

35

498,8

496,1

-9,2729

-10,2746

95,2749

85,9863

105,5669

36

501,5

498,8

-6,5729

-7,5746

49,7868

43,2028

57,3742

37

541

501,5

32,9271

-4,8746

-160,5058

1084,1951

23,7615

38

512,3

541

4,2271

34,6254

146,3658

17,8685

1198,9200

39

512,6

512,3

4,5271

5,9254

26,8251

20,4948

35,1106

40

511,5

512,6

3,4271

6,2254

21,3353

11,7451

38,7559

41

511,9

511,5

3,8271

5,1254

19,6156

14,6468

26,2700

42

513,9

511,9

5,8271

5,5254

32,1973

33,9553

30,5303

43

520

513,9

11,9271

7,5254

89,7566

142,2562

56,6320

44

515,9

520

7,8271

13,6254

106,6478

61,2638

185,6522

45

524,2

515,9

16,1271

9,5254

153,6176

260,0840

90,7337

46

527,1

524,2

19,0271

17,8254

339,1665

362,0312

317,7457

47

529,8

527,1

21,7271

20,7254

450,3037

472,0677

429,5432

48

534,9

529,8

26,8271

23,4254

628,4366

719,6943

548,7505

49

578,2

534,9

70,1271

28,5254

2000,4058

4917,8128

813,6998

50

539,4

578,2

31,3271

71,8254

2250,0836

981,3884

5158,8915

51

545,3

539,4

37,2271

33,0254

1229,4414

1385,8584

1090,6786

52

551,9

545,3

43,8271

38,9254

1705,9892

1920,8163

1515,1886

53

549,7

551,9

41,6271

45,5254

1895,0922

1732,8170

2072,5642

54

550,1

549,7

42,0271

43,3254

1820,8427

1766,2787

1877,0923

55

554

550,1

45,9271

43,7254

2008,1827

2109,3002

1911,9127

56

550

554

41,9271

47,6254

1996,7968

1757,8833

2268,1810

57

565,6

550

57,5271

43,6254

2509,6449

3309,3694

1903,1776

58

564,7

565,6

56,6271

59,2254

3353,7651

3206,6306

3507,6508

59

566,9

564,7

58,8271

58,3254

3431,1166

3460,6299

3401,8551

60

572,7

566,9

64,6271

60,5254

3911,5837

4176,6645

3663,3269

Итого

29973,6

29876,1

46980,9093

52640,2766

49558,8719

Рассчитав коэффициент автокорреляции второго порядка r₂, получим количественную характеристику корреляционной связи рядов , : .

Аналогично рассчитаем коэффициент автокорреляции третьего порядка: .

Можно сделать вывод, что наиболее целесообразно построение уравнения авторегрессии так как значение свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 1 месяц.