Экономическое планирование методами математической статистики

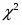
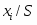
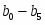
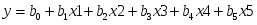
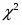
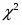
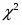
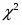
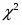
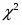
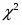
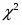
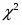
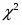
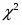
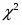
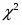УДК

КП

Министерство образования Украины

Харьковский государственный технический университет радиоэлектроники

Кафедра ПОЭВМ

Комплексная курсовая работа

по курсу «Вероятностные процессы и математическая статистика в автоматизированных системах»

Тема: «Провести экономическую оценку эффективности работы предприятия. Провести долгосрочное планирование работы методом множественной линейной регрессии. Построить математическую модель повышения эффективности работы».

Выполнил:

Ст. гр. ПОВТАС-96-3 Фурсов Я. А.

Руководитель: асс. Шамша Т. Б.

Комиссия: проф. к. т. н. Дударь З. В.

проф. к.. т. н. Лесная Н. С.

асс. Шамша Т. Б.

1999

РЕФЕРАТ

Пояснительная записка к комплексной курсовой работе: 30 с.,

17 табл., 4 источника.

Цель задания – произвести статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.

Работа посвящена исследованию экономической деятельности предприятия методами статистического анализа. В качестве исходных данных принимается некоторая совокупность выборок по экономическим показателям, в частности прибыли, затратах, ценах и т.д. за некоторый отчетный период работы предприятия. В работе к этому набору данных применяются различные методы статистического анализа, направленные на установление вида зависимости прибыли предприятия от других экономических показателей. На основании полученных результатов методами регрессионного анализа построенна математическая модель и оценена ее адекватность. Помимо этого проведен временной анализ показателей прибыли за 4 года и выявлены закономерности изменения прибыли по месяцам. На основании этих данных проведено прогнозирование прибыли на следующий (текущий) год.

Работа выполнена в учебных целях.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, РЕГРЕССИОННЫЙ АНАЛИЗ, МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ, УРОВЕНЬ ЗНАЧИМОСТИ, КРИТЕРИЙ СЕРИЙ, КРИТЕРИЙ ИНВЕРСИЙ, КРИТЕРИЙ , ТРЕНД

СОДЕРЖАНИЕ

Введение 4

Постановка задачи 5

2.Предварительный анализ исходных данных……………………………7

3. Построение математической модели…………………………………….24

Выводы……………………………………………………………………….29

Перечень ссылок .30

ВВЕДЕНИЕ

Не вызывает сомнения тот факт, что организация любого производства без тщательного теоретического обоснования, экономических расчетов и прогнозирования – это растраченные впустую средства. Еще 10 лет назад такая подготовка занимала большое количество времени и средств, поскольку требовала значительного персонала и вычислительных мощностей. В настоящее время уровень развития вычислительной техники позволяет производить сложные статистические исследования при минимальных затратах рабочего времени, персонала и средств, что сделало их доступными для бухгалтерии каждого предприятия.

Безусловно, в условиях рыночной экономики, главным показателем рентабельности предприятия является прибыль. Поэтому очень важно понять, как необходимо вести хозяйство, что бы как говориться «не вылететь в трубу». И здесь незаменимы методы математической статистики, которые позволяют правильно оценить, какие факторы, и в какой степени влияют на прибыль, а так же на основании правильно построенной математической модели, спрогнозировать прибыль на будущий период.

1 ПОСТАНОВКА ЗАДАЧИ

Цель курсового проекта - сформировать профессиональные умения и навыки применения методов математической статистики к практическому анализу реальных физических процессов.

Исходные данные для поставленного задания приведены в

таблице 1.1

Таблица 1.1 – Исходные данные для регрессионного анализа.

Прибыль

Коэффициент качества продукции

Доля в общем объеме продаж

Розничная цена

Коэффициент издержек на 1 продукции

Удовлетворение условий розничных торговцев

№

Y, %

1,99

1,22

1,24

1,3

35,19

2,08

12,21

1,45

1,54

1,04

1,09

23,07

1,9

1,31

23,31

2,28

24,14

2,53

1,36

1,64

1,44

35,05

3,41

2,65

1,19

1,75

36,87

1,96

1,63

1,26

68,84

1,54

4,7

2,71

1,66

1,28

0,47

58,45

1,76

1,4

1,42

30,32

2,51

59,55

2,09

2,61

1,65

2,81

61,42

1,1

2,42

1,24

32,94

0,59

61,51

3,62

3,5

1,09

28,56

0,64

61,95

3,53

1,29

78,75

1,73

71,24

2,09

2,44

1,65

38,63

1,83

71,45

1,54

2,6

1,19

48,67

0,76

Продолжение таблицы 1.1

81,88

2,41

2,11

1,64

40,83

0,14

10,08

3,64

2,06

1,46

3,53

10,25

2,61

1,85

1,59

2,13

10,81

2,62

2,28

1,57

3,86

11,09

3,29

4,07

1,78

1,28

12,64

1,24

1,84

1,38

31,2

4,25

12,92

1,37

1,9

1,55

29,49

3,98

Основная цель первой части задания оценить влияние на прибыль предприятия от реализации продукции одного вида следующих факторов:

Х1 - коэффициент качества продукции;
Х2 - доля в общем объеме продаж;
Х3 – розничная цена продукции;
Х4 – коэффициент издержек на единицу продукции;
Х5 – удовлетворение условий розничных торговцев.

Необходимо, применив регрессионные методы анализа, построить математическую модель зависимости прибыли от некоторых (или всех ) из вышеперечисленных факторов и проверить адекватность полученной модели.

2 Предварительный анализ исходных данных

Прежде чем применить к имеющимся у нас исходным данным метод регрессионного анализа, необходимо провести некоторый предварительный анализ имеющихся в нашем распоряжении выборок. Это позволит сделать выводы о качестве имеющихся в нашем распоряжении данных, а именно: о наличии или отсутствии тренда, нормальном законе распределения выборки, оценить некоторые статистические характеристики и т.д.

Для всех последующих расчетов примем уровень значимости 0.05, что соответствует 5% вероятности ошибки.

2.1 Исследование выборки по прибыли (Y).

Математическое ожидание (арифметическое среднее)

34,91761905.

Доверительный интервал для математического

ожидания (22,75083;47,08441).

Дисперсия (рассеивание) 714,402159.
Доверительный интервал для дисперсии (439,0531; 1564,384).
Средне квадратичное отклонение (от среднего) 26,72830258.
Медиана выборки 24,14.
Размах выборки 79,89.
Асимметрия (смещение от нормального распределения) 0,370221636.
Эксцесс выборки (отклонение от нормального распределения)

-1,551701276.

Коэффициент вариации (коэффициент представительности среднего) 77%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.1 (2-й столбец). Сумма серий равняется 5. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.1 (3-й столбец). Сумма инверсий равняется 81. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.1 – Критерии серий и инверсий.

Прибыль Y %

Критерий серий

Критерий инверсий

1,99

12,21

23,07

24,14

35,05

36,87

4,7

58,45

59,55

61,42

61,51

61,95

71,24

71,45

81,88

10,08

Продолжение таблицы 2.1

10,25

10,81

11,09

12,64

12,92

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 10,69132103. Получим следующее количество интервалов группировки размах/длина интервала=7.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.2.

Таблица 2.2 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

12,68132103

0,221751084

23,37264207

0,285525351

34,0639631

0,313282748

44,75528414

0,2929147

55,44660517

0,233377369

66,1379262

0,158448887

76,82924724

0,091671119

Результирующее значение критерия 2,11526E-55 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.

Исследование выборки по коэффициенту качества продукции (Х1).

Математическое ожидание (арифметическое среднее) 2,29.
Доверительный интервал для математического ожидания (1,905859236; 2,674140764).
Дисперсия (рассеивание) 0,71215.
Доверительный интервал для дисперсии (0,437669008; 1,559452555).
Средне квадратичное отклонение (от среднего) 0,843889803.
Медиана выборки 2,09.
Размах выборки 2,54.
Асимметрия (смещение от нормального распределения) 0,290734565.
Эксцесс выборки (отклонение от нормального распределения)

-1,161500717.

Коэффициент вариации (коэффициент представительности среднего) 37%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.3 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.3 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.3 – Критерии серий и инверсий.

Коэффициент качества продукции Х1

Критерий серий

Критерий инверсий

1,22

1,45

1,9

2,53

3,41

1,96

2,71

1,76

2,09

1,1

3,62

3,53

2,09

1,54

2,41

3,64

2,61

2,62

3,29

1,24

1,37

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,337555921. Получим следующее количество интервалов группировки размах/длина интервала=7.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.4.

Таблица 2.4 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

1,437555921

5,960349765

1,775111843

8,241512255

2,112667764

9,71079877

2,450223685

9,750252967

2,787779606

8,342374753

3,125335528

6,082419779

3,462891449

3,778991954

Результирующее значение критерия 0,000980756 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.

2.3 Исследование выборки по доле в общем объеме продаж (Х2).

Математическое ожидание (арифметическое среднее) 2,083809524.
Доверительный интервал для математического ожидания (1,748443949; 2,419175098).
Дисперсия (рассеивание) 0,542784762.
Доверительный интервал для дисперсии (0,333581504; 1,188579771).
Средне квадратичное отклонение (от среднего) 0,736739277.
Медиана выборки 1,9.
Размах выборки 2,83.
Асимметрия (смещение от нормального распределения) 1,189037981.
Эксцесс выборки (отклонение от нормального распределения)

1,48713312.

Коэффициент вариации (коэффициент представительности среднего) 35%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.5 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.5 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.5 – Критерии серий и инверсий.

Коэффициент качества продукции Х2

Критерий серий

Критерий инверсий

1,24

1,54

1,31

1,36

2,65

Продолжение таблицы 2.5

1,63

1,66

1,4

2,61

2,42

3,5

1,29

2,44

2,6

2,11

2,06

1,85

2,28

4,07

1,84

1,9

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,294695711. Получим следующее количество интервалов группировки размах/длина интервала=9.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.6.

Таблица 2.6 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

1,534695711

8,613638207

1,829391421

10,71322271

2,124087132

11,35446101

2,418782843

10,25476697

2,713478553

7,892197623

3,008174264

5,175865594

3,302869975

2,892550245

3,597565686

1,377500344

3,892261396

0,559004628

Результирующее значение критерия 0,000201468 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.

2.4 Исследование выборки по розничной цене (Х3).

Математическое ожидание (арифметическое среднее) 1,390952381.
Доверительный интервал для математического ожидания (1,287631388; 1,494273374).
Дисперсия (рассеивание) 0,051519048.
Доверительный интервал для дисперсии (0,031662277; 0,112815433).
Средне квадратичное отклонение (от среднего) 0,226978077.
Медиана выборки 1,38.
Размах выборки 0,78.
Асимметрия (смещение от нормального распределения) -0,060264426.
Эксцесс выборки (отклонение от нормального распределения)

-1,116579819.

Коэффициент вариации (коэффициент представительности среднего) 16%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.7 (2-й столбец). Сумма серий равняется 8. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.7 (3-й столбец). Сумма инверсий равняется 68. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.7 – Критерии серий и инверсий.

Розничная цена Х4

Критерий серий

Критерий инверсий

1,3

1,04

1,64

1,19

Продолжение таблицы 2.7

1,26

1,28

1,42

1,65

1,24

1,09

1,29

1,65

1,19

1,64

1,46

1,59

1,57

1,78

1,38

1,55

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,090791231. Получим следующее количество интервалов группировки размах/длина интервала=8.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.8.

Таблица 2.8 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

1,090791231

15,39563075

1,181582462

24,12028441

1,272373693

32,20180718

1,363164924

36,63455739

1,453956155

35,51522214

1,544747386

29,33938492

1,635538617

20,65381855

1,726329848

12,38975141

Результирующее значение критерия 3,27644E-33 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.

2.5 Исследование выборки по коэффициенту издержек на единицу продукции (Х4).

Математическое ожидание (арифметическое среднее) 57,46333333.
Доверительный интервал для математического ожидания (46,70536237; 68,22130429).
Дисперсия (рассеивание) 558,5363233.
Доверительный интервал для дисперсии (343,2620073; 1223,072241).
Средне квадратичное отклонение (от среднего) 23,63337308.
Медиана выборки 68,84.
Размах выборки 56,69.
Асимметрия (смещение от нормального распределения) --0,199328538.
Эксцесс выборки (отклонение от нормального распределения)

-1,982514776.

Коэффициент вариации (коэффициент представительности среднего) 41%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.9 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.9 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.9 – Критерии серий и инверсий

Розничная цена Х4

Критерий серий

Критерий инверсий

35,19

23,31

Продолжение таблицы 2.9.

68,84

30,32

32,94

28,56

78,75

38,63

48,67

40,83

31,2

29,49

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 9,453349234. Получим следующее количество интервалов группировки размах/длина интервала=5.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.10.

Таблица 2.10 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

32,76334923

0,205311711

42,21669847

0,287891016

51,6700477

0,343997578

61,12339693

0,350264029

70,57674617

0,30391251

2.6 Исследование выборки по коэффициенту удовлетворения условий розничных торговцев (Х5).

Математическое ожидание (арифметическое среднее) 1,937619048.
Доверительный интервал для математического ожидания (1,390131506; 2,485106589).
Дисперсия (рассеивание) 1,446569048.
Доверительный интервал для дисперсии (0,889023998; 3,167669447).
Средне квадратичное отклонение (от среднего) 1,202733989.
Медиана выборки 1,75.
Размах выборки 4,11.
Асимметрия (смещение от нормального распределения) --0,527141402.
Эксцесс выборки (отклонение от нормального распределения)

-0,580795634.

Коэффициент вариации (коэффициент представительности среднего) 62%.

Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 2.11 (2-й столбец). Сумма серий равняется 13. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 2.11 (3-й столбец). Сумма инверсий равняется 80. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.

Таблица 2.11 – Критерии серий и инверсий.

Розничная цена Х4

Критерий серий

Критерий инверсий

2,08

1,09

2,28

1,44

1,75

1,54

Продолжение таблицы 2.11

0,47

2,51

2,81

0,59

0,64

1,73

1,83

0,76

0,14

3,53

2,13

3,86

1,28

4,25

3,98

Итого

Проверка гипотезы о нормальном законе распределения выборки с применением критерия . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,481093595. Получим следующее количество интервалов группировки размах/длина интервала=8.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 2.12.

Таблица 2.12 – Критерий .

Интервалы группировки

Теоретическая частота

Расчетная частота

0,621093595

3,826307965

1,102187191

5,47254967

1,583280786

6,669793454

2,064374382

6,927043919

2,545467977

6,130506823

3,026561573

4,623359901

3,507655168

2,971200139

3,988748764

1,627117793

Результирующее значение критерия 0,066231679 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.

Построение математической модели

Корреляционный анализ.

Для оценки степени зависимости между переменными модели построим корреляционную матрицу, и для каждого коэффициента корреляции в матрице рассчитаем V-функцию, которая служит для проверки гипотезы об отсутствии корреляции между переменными.

Таблица 3.1. – Корреляционная матрица

0,95238

0,00950

0,21252

-0,01090

-0,30012

-0,42102

8,30380

0,04247

0,96511

-0,04873

-1,38479

-2,00769

0,00950

0,95238

0,36487

0,13969

0,50352

-0,12555

0,04247

8,30380

1,71054

0,62883

2,47761

-0,56445

0,21252

0,36487

0,95238

0,23645

0,06095

-0,19187

0,96511

1,71054

8,30380

1,07781

0,27291

-0,86885

-0,01090

0,13969

0,23645

0,95238

0,24228

0,25014

-0,04873

0,62883

1,07781

8,30380

1,10549

1,14293

-0,30012

0,50352

0,06095

0,24228

0,95238

-0,03955

-1,38479

2,47761

0,27291

1,10549

8,30380

-0,17694

-0,42102

-0,12555

-0,19187

0,25014

-0,03955

0,95238

-2,00769

-0,56445

-0,86885

1,14293

-0,17694

8,30380

Гипотеза о нулевой корреляции принимается при –1,96<V<1,96, значения, для которых это условие не выполняется, выделены жирным шрифтом цветом. Следовательно, значимая зависимость имеет место между Y и Х5, а также Х1 и Х4.

Регрессионный анализ.

Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью (иначе Y) и факторами на нее влияющими (Х1, Х2, Х3, Х4, Х5). Следовательно, математическая модель может быть описана уравнением вида:

, (3.1)

где - линейно-независимые постоянные коэффициенты.

Для их отыскания применим множественный регрессионный анализ. Результаты регрессии сведены в таблицы 3.2 – 3.4.

Таблица 3.2.-Регрессионная статистика.

Множественный R

0,609479083

R-квадрат

0,371464753

Нормированный R-квадрат

0,161953004

Стандартная ошибка

24,46839969

Наблюдения

Таблица 3.3. –Дисперсионная таблица.

Степени свободы

Значимость F

Регрессия

5307,504428

1061,500886

1,773002013

0,179049934

Остаток

8980,538753

598,7025835

Итого

14288,04318

Таблица 3.4 – Коэффициенты регрессии.

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

38,950215

35,7610264

1,0891805

0,29326

-37,272

115,173

-37,2726

115,173

4,5371110

8,42440677

0,5385674

0,59808

-13,419

22,4933

-13,4190

22,4933

1,8305781

8,73999438

0,2094484

0,83691

-16,798

20,4594

-16,7982

20,4594

23,645979

27,4788285

0,8605162

0,40304

-34,923

82,2157

-34,9237

82,2157

-0,526248

0,28793074

-1,827690

0,08755

-1,1399

0,08746

-1,13995

0,08746

-10,780037

4,95649626

-2,174931

0,04604

-21,344

-0,21550

-21,3445

-0,21550

Таким образом, уравнение, описывающее математическую модель, приобретает вид:

Y=4,53711108952303*X1+1,830578196*X2+23,64597929*X3- 0,526248308*X5-10,78003746*X5+38,95021506. (3.2)

Для оценки влияния каждого из факторов на результирующую математическую модель применим метод множественной линейной регрессии к нормированным значениям переменных , результаты пересчета коэффициентов приведены в таблице 3.5.

Таблица 3.5. – Оценка влияния факторов.

Коэффициенты

Стандартная ошибка

t-статистика

Y-пересечение

38,95021506

35,76102644

1,089180567

Переменная X 1

3,828821785

7,109270974

0,538567428

Переменная X 2

1,348658856

6,439097143

0,209448441

Переменная X 3

5,367118917

6,237091662

0,86051628

Переменная X 4

-12,43702261

6,804774783

-1,827690556

Переменная X 5

-12,96551745

5,961346518

-2,174931018

Коэффициенты в таблице 3.5 показывают степень влияния каждой из переменных на результат (Y). Чем больше коэффициент, тем сильнее прямая зависимость (отрицательные коэффициенты показывают обратную зависимость).

F-критерий из таблицы 3.3 показывает степень адекватности полученной математической модели.

ВЫВОДЫ

В результате проведенной работы был произведен статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построена адекватная математическая модель и спрогнозирована прибыль на последующие периоды.

В процессе выполнения работы изучили и научились применять на практике следующие методы математической статистики:

линейный регрессионный анализ,
множественный регрессионный анализ,
корреляционный анализ,
проверка стационарности и независимости выборок,
выявление тренда,
критерий .

Перечень ссылок

Бендод Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. – М.: Мир, 1989.
Математическая статистика. Под ред. А. М. Длина, М.: Высшая школа, 1975.
Л.Н.Большев, Н.В.Смирнов. Таблицы математической статистики.-М.: Наука, 1983.
Н.Дрейпер, Г.Смит. Прикладной регрессионный анализ. Пер. с англ.- М.: Статистика, 1973.

Вероятностные ряды ID

Месяц

1994

1996

1997

1998

Январь

1500000

1650000

1400000

1700000

Февраль

900000

850000

890000

1200000

Март

700000

600000

550000

459000

Апрель

300000

125000

250000

221000

Май

400000

300000

100000

1000

Июнь

250000

450000

150000

250000

Июль

200000

600000

132000

325000

Август

150000

750000

142000

354000

Сентябрь

300000

254000

150000

Октябрь

250000

259000

350000

100000

Ноябрь

400000

453000

450000

259000

Декабрь

2000000

1700000

1000000

1900000

Регрессионный анализ ID

Прибыль

Коэффициент качества продукции

Доля в общем объеме продаж

Розничная цена

Коэффициент издержек на 1 продукции

Удовлетворение условий розничных торговцев

№

Y, %

1,99

1,22

1,24

1,3

35,19

2,08

12,21

1,45

1,54

1,04

1,09

23,07

1,9

1,31

23,31

2,28

24,14

2,53

1,36

1,64

1,44

35,05

3,41

2,65

1,19

1,75

36,87

1,96

1,63

1,26

68,84

1,54

4,7

2,71

1,66

1,28

0,47

58,45

1,76

1,4

1,42

30,32

2,51

59,55

2,09

2,61

1,65

2,81

61,42

1,1

2,42

1,24

32,94

0,59

61,51

3,62

3,5

1,09

28,56

0,64

61,95

3,53

1,29

78,75

1,73

71,24

2,09

2,44

1,65

38,63

1,83

71,45

1,54

2,6

1,19

48,67

0,76

81,88

2,41

2,11

1,64

40,83

0,14

10,08

3,64

2,06

1,46

3,53

10,25

2,61

1,85

1,59

2,13

10,81

2,62

2,28

1,57

3,86

11,09

3,29

4,07

1,78

1,28

12,64

1,24

1,84

1,38

31,2

4,25

12,92

1,37

1,9

1,55

29,49

3,98

Среднее по столбцу

M(X)

34,91761905

2,29

2,083809524

1,390952381

57,46333333

1,937619048

Дисперсия по столбцу

D(X)

714,402159

0,71215

0,542784762

0,051519048

558,5363233

1,446569048

26,72830258

0,843889803

0,736739277

0,226978077

23,63337308

1,202733989

Ковариционная матрица

680,3830086

0,214214286

4,18483288

-0,066102494

-189,5780492

-13,53461519

0,214214286

0,678238095

0,226847619

0,026757143

10,04216667

-0,127428571

4,18483288

0,226847619

0,516937868

0,039539229

1,061201587

-0,170019501

-0,066102494

0,026757143

0,039539229

0,04906576

1,29965873

0,068287982

-189,5780492

10,04216667

1,061201587

1,29965873

531,9393556

-1,12405873

-13,53461519

-0,127428571

-0,170019501

0,068287982

-1,12405873

1,377684807

Отклонение от среднего

-32,92761905

-1,07

-0,843809524

-0,090952381

-22,27333333

0,142380952

-22,70761905

-0,84

-0,543809524

-0,350952381

22,53666667

-0,847619048

-11,84761905

-0,39

-0,773809524

-0,390952381

-34,15333333

0,342380952

-10,77761905

0,24

-0,723809524

0,249047619

22,53666667

-0,497619048

0,132380952

1,12

0,566190476

-0,200952381

22,53666667

-0,187619048

1,952380952

-0,33

-0,453809524

-0,130952381

11,37666667

-0,397619048

-30,21761905

0,42

-0,423809524

-0,110952381

22,53666667

-1,467619048

23,53238095

-0,53

-0,683809524

0,029047619

-27,14333333

0,572380952

24,63238095

-0,2

0,526190476

0,259047619

22,53666667

0,872380952

26,50238095

-1,19

0,336190476

-0,150952381

-24,52333333

-1,347619048

26,59238095

1,33

1,416190476

-0,300952381

-28,90333333

-1,297619048

27,03238095

1,24

-0,793809524

-0,100952381

21,28666667

-0,207619048

36,32238095

-0,2

0,356190476

0,259047619

-18,83333333

-0,107619048

36,53238095

-0,75

0,516190476

-0,200952381

-8,793333333

-1,177619048

46,96238095

0,12

0,026190476

0,249047619

-16,63333333

-1,797619048

-24,83761905

1,35

-0,023809524

0,069047619

22,53666667

1,592380952

-24,66761905

0,32

-0,233809524

0,199047619

22,53666667

0,192380952

-24,10761905

0,33

0,196190476

0,179047619

22,53666667

1,922380952

-23,82761905

1,986190476

0,389047619

22,53666667

-0,657619048

-22,27761905

-1,05

-0,243809524

-0,010952381

-26,26333333

2,312380952

-21,99761905

-0,92

-0,183809524

0,159047619

-27,97333333

2,042380952

Погрешность

-2,84217E-14

-9,10383E-15

4,26326E-14

-5,32907E-15

Квадраты отклонений от среднего

1084,228096

1,1449

0,712014512

0,008272336

496,1013778

0,020272336

515,6359628

0,7056

0,295728798

0,123167574

507,9013444

0,71845805

140,3660771

0,1521

0,598781179

0,152843764

1166,450178

0,117224717

116,1570723

0,0576

0,523900227

0,062024717

507,9013444

0,247624717

0,017524717

1,2544

0,320571655

0,040381859

507,9013444

0,035200907

3,811791383

0,1089

0,205943084

0,017148526

129,4285444

0,158100907

913,1045009

0,1764

0,179614512

0,012310431

507,9013444

2,153905669

553,7729533

0,2809

0,467595465

0,000843764

736,7605444

0,327619955

606,7541914

0,04

0,276876417

0,067105669

507,9013444

0,761048526

702,3761961

1,4161

0,113024036

0,022786621

601,3938778

1,816077098

707,1547247

1,7689

2,005595465

0,090572336

835,4026778

1,683815193

730,74962

1,5376

0,63013356

0,010191383

453,1221778

0,043105669

1319,315358

0,04

0,126871655

0,067105669

354,6944444

0,011581859

1334,614858

0,5625

0,266452608

0,040381859

77,32271111

1,386786621

2205,465225

0,0144

0,000685941

0,062024717

276,6677778

3,23143424

616,90732

1,8225

0,000566893

0,004767574

507,9013444

2,535677098

608,4914295

0,1024

0,054666893

0,039619955

507,9013444

0,037010431

581,1772961

0,1089

0,038490703

0,03205805

507,9013444

3,695548526

567,7554295

3,944952608

0,15135805

507,9013444

0,432462812

496,2923104

1,1025

0,059443084

0,000119955

689,7626778

5,347105669

483,8952438

0,8464

0,033785941

0,025296145

782,5073778

4,171319955

Дисперсия по столбцу

714,402159

0,71215

0,542784762

0,051519048

558,5363233

1,446569048

Кореляционная матрица

0,952380952

0,009497107

0,212516628

-0,010895886

-0,300117251

-0,421022155

8,30379958

0,042473629

0,965111718

-0,048729813

-1,384789996

-2,007692777

0,009497107

0,952380952

0,364867065

0,139691534

0,503519129

-0,125548489

0,042473629

8,30379958

1,710542787

0,628831315

2,477605293

-0,564448173

0,212516628

0,364867065

0,952380952

0,236445177

0,060947845

-0,191873647

0,965111718

1,710542787

8,30379958

1,077808965

0,272905301

-0,868854214

-0,010895886

0,139691534

0,236445177

0,952380952

0,242281194

0,250144398

-0,048729813

0,628831315

1,077808965

8,30379958

1,105494772

1,142929664

-0,300117251

0,503519129

0,060947845

0,242281194

0,952380952

-0,039545194

-1,384789996

2,477605293

0,272905301

1,105494772

8,30379958

-0,176943758

-0,421022155

-0,125548489

-0,191873647

0,250144398

-0,039545194

0,952380952

-2,007692777

-0,564448173

-0,868854214

1,142929664

-0,176943758

8,30379958

Область принятия гипотезы

-1,96

1,96

Регрессия

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R

0,009971962

R-квадрат

9,944E-05

Нормированный R-квадрат

-0,052526905

Стандартная ошибка

27,42129635

Наблюдения

Дисперсионный анализ

Значимость F

Регрессия

1,42080336

0,001889548

0,965781312

Остаток

14286,62238

751,9274936

Итого

14288,04318

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Нижние 95,0%

Верхние 95,0%

Y-пересечение

34,19434691

17,68210005

1,933839692

0,068170144

-2,814725323

71,20341915

-2,814725323

71,20341915

Переменная X 1

0,31583936

7,265863675

0,043468936

0,965781312

-14,89179281

15,52347153

-14,89179281

15,52347153

ВЫВОД ОСТАТКА

Наблюдение

Предсказанное Y

Остатки

Стандартные остатки

34,57967093

-32,58967093

-1,280111564

34,65231399

-22,44231399

-0,881526718

34,7944417

-11,7244417

-0,460532217

34,99342049

-10,85342049

-0,42631879

34,81339206

2,056607941

0,080782884

35,05027158

-30,35027158

-1,192148693

34,75022419

23,69977581

0,930919405

34,85445118

24,69554882

0,970033042

34,54177021

26,87822979

1,055768033

35,3376854

26,1723146

1,028039916

35,30925985

26,64074015

1,046439518

34,68073953

36,76926047

1,444284467

34,95551977

46,92448023

1,843178162

35,34400218

-25,26400218

-0,992361703

35,01868764

-24,76868764

-0,972905911

35,02184604

-24,21184604

-0,951033355

35,23345841

-24,14345841

-0,948347112

34,58598772

-21,94598772

-0,862031185

34,62704684

-21,70704684

-0,852645666

Анализ У

Прибыль

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

Y, %

1,99

12,68132103

0,221751084

12,21

23,37264207

0,285525351

23,07

34,0639631

0,313282748

24,14

44,75528414

0,2929147

35,05

55,44660517

0,233377369

36,87

66,1379262

0,158448887

4,7

76,82924724

0,091671119

58,45

59,55

61,42

61,51

61,95

71,24

71,45

81,88

10,08

10,25

10,81

11,09

12,64

12,92

Среднее по столбцу

Доверительный интервал

34,91761905

22,75082838

47,08440971

Дисперсия по столбцу

Доверительный интервал

714,402159

439,0531267

1564,38429

Cреднее квадратичное отклонение

Хи-квадрат критерий

26,72830258

Критерий серий

4,6762E-100

Медиана

мин.

рассчетное

макс.

24,14

Табличное значение

Размах

тренд отсутствует

12,6

79,89

Вариация

Критерий инверсий

77%

мин.

рассчетное

макс.

Ассиметрия

125

0,370221636

тренд отсутствует

Эксцес

-1,551701276

Анализ X1

Коэффициент качества продукции

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

1,22

1,437555921

5,960349765

1,45

1,775111843

8,241512255

1,9

2,112667764

9,71079877

2,53

2,450223685

9,750252967

3,41

2,787779606

8,342374753

1,96

3,125335528

6,082419779

2,71

3,462891449

3,778991954

1,76

2,09

1,1

3,62

3,53

2,09

1,54

2,41

3,64

2,61

2,62

3,29

1,24

1,37

Среднее по столбцу

Доверительный интервал

2,29

1,905859236

2,674140764

Дисперсия по столбцу

Доверительный интервал

0,71215

0,437669008

1,559452555

Cреднее квадратичное отклонение

Хи-квадрат критерий

0,843889803

Критерий серий

0,000980756

Медиана

мин.

рассчетное

макс.

2,09

Табличное значение

Размах

тренд отсутствует

12,6

2,54

Вариация

Критерий инверсий

37%

мин.

рассчетное

макс.

Ассиметрия

125

0,290734565

тренд отсутствует

Эксцес

-1,161500717

Анализ Х2

Доля в общем объеме продаж

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

1,24

1,534695711

8,613638207

1,54

1,829391421

10,71322271

1,31

2,124087132

11,35446101

1,36

2,418782843

10,25476697

2,65

2,713478553

7,892197623

1,63

3,008174264

5,175865594

1,66

3,302869975

2,892550245

1,4

3,597565686

1,377500344

2,61

3,892261396

0,559004628

2,42

3,5

1,29

2,44

2,6

2,11

2,06

1,85

2,28

4,07

1,84

1,9

Среднее по столбцу

Доверительный интервал

2,083809524

1,748443949

2,419175098

Дисперсия по столбцу

Доверительный интервал

0,542784762

0,333581504

1,188579771

Cреднее квадратичное отклонение

Хи-квадрат критерий

0,736739277

Критерий серий

0,000201468

Медиана

мин.

рассчетное

макс.

1,9

Табличное значение

Размах

тренд отсутствует

12,6

2,83

Вариация

Критерий инверсий

35%

мин.

рассчетное

макс.

Ассиметрия

125

1,189037981

тренд отсутствует

Эксцес

1,48713312

Анализ Х3

Розничная цена

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

1,3

1,090791231

15,39563075

1,04

1,181582462

24,12028441

1,272373693

32,20180718

1,64

1,363164924

36,63455739

1,19

1,453956155

35,51522214

1,26

1,544747386

29,33938492

1,28

1,635538617

20,65381855

1,42

1,726329848

12,38975141

1,65

1,24

1,09

1,29

1,65

1,19

1,64

1,46

1,59

1,57

1,78

1,38

1,55

Среднее по столбцу

Доверительный интервал

1,390952381

1,287631388

1,494273374

Дисперсия по столбцу

Доверительный интервал

0,051519048

0,031662277

0,112815433

Cреднее квадратичное отклонение

Хи-квадрат критерий

0,226978077

Критерий серий

3,27644E-33

Медиана

мин.

рассчетное

макс.

1,38

Табличное значение

Размах

тренд отсутствует

12,6

0,78

Вариация

Критерий инверсий

16%

мин.

рассчетное

макс.

Ассиметрия

125

-0,060264426

тренд отсутствует

Эксцес

-1,116579819

Анализ Х4

Коэффициент издержек на 1 продукции

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

35,19

32,76334923

0,205311711

42,21669847

0,287891016

23,31

51,6700477

0,343997578

61,12339693

0,350264029

70,57674617

0,30391251

68,84

30,32

32,94

28,56

78,75

38,63

48,67

40,83

31,2

29,49

Среднее по столбцу

Доверительный интервал

57,46333333

46,70536237

68,22130429

Дисперсия по столбцу

Доверительный интервал

558,5363233

343,2620073

1223,072241

Cреднее квадратичное отклонение

Хи-квадрат критерий

23,63337308

Критерий серий

7,37999E-32

Медиана

мин.

рассчетное

макс.

68,84

Табличное значение

Размах

тренд отсутствует

12,6

56,69

Вариация

Критерий инверсий

41%

мин.

рассчетное

макс.

Ассиметрия

125

-0,199328538

тренд отсутствует

Эксцес

-1,982514776

Анализ Х5

Удовлетворение условий розничных торговцев

Критерий серий

Критерий инверсий

Расчетная частота

Интервалы группировки

Теоретическая частота

2,08

0,621093595

3,826307965

1,09

1,102187191

5,47254967

2,28

1,583280786

6,669793454

1,44

2,064374382

6,927043919

1,75

2,545467977

6,130506823

1,54

3,026561573

4,623359901

0,47

3,507655168

2,971200139

2,51

3,988748764

1,627117793

2,81

0,59

0,64

1,73

1,83

0,76

0,14

3,53

2,13

3,86

1,28

4,25

3,98

Среднее по столбцу

Доверительный интервал

1,937619048

1,390131506

2,485106589

Дисперсия по столбцу

Доверительный интервал

1,446569048

0,889023998

3,167669447

Cреднее квадратичное отклонение

Хи-квадрат критерий

1,202733989

Критерий серий

0,066231679

Медиана

мин.

рассчетное

макс.

1,75

Табличное значение

Размах

тренд отсутствует

12,6

4,11

Вариация

Критерий инверсий

62%

мин.

рассчетное

макс.

Ассиметрия

125

0,527141402

тренд отсутствует

Эксцес

-0,580795634

Листать вверх Листать вниз

Получить код

Скачать материал (0.09 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории экономико-математическое моделирование:

Расчет развозочно-сборочных маршрутов

Разработка программных средств анализа графика функции и решение оптимизационных задач

Анализ расчетов с поставщиками и покупателями

Моделирование хозяйственной деятельности предприятия

Применение математического моделирования в экономике

Динамика рыночной экономики

Статистика оборотных фондов