Математические методы и модели
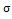
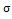
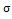
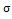
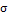
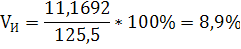
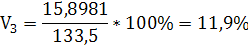
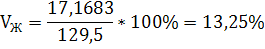
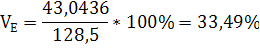
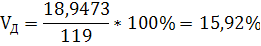
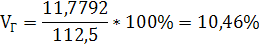
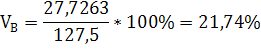
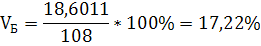
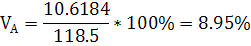
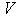
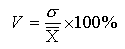
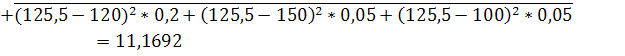
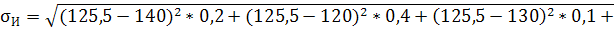
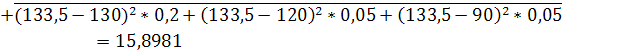
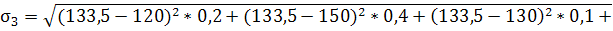
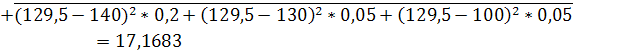
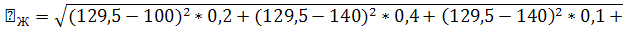
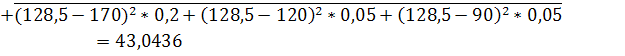
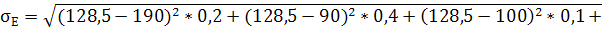
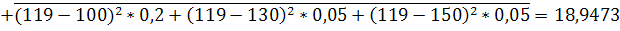
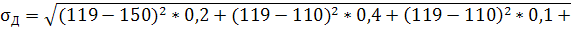
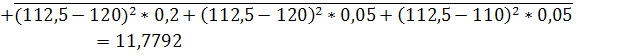
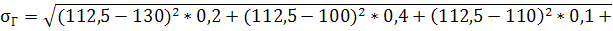
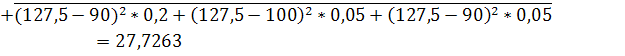
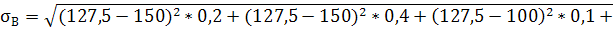
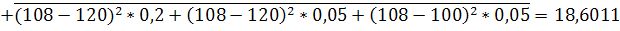
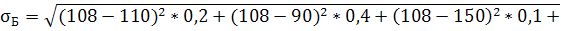
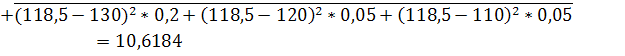
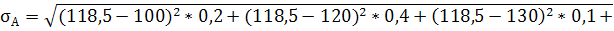
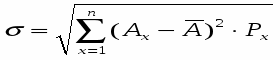
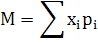
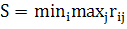
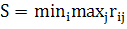
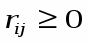
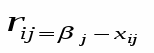
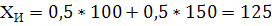
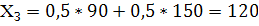
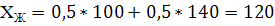
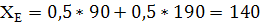
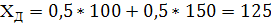
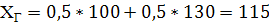
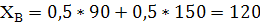
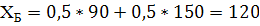
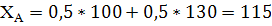
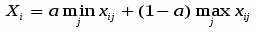
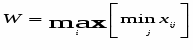
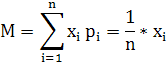
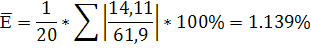

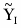
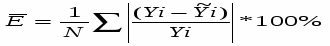
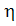
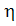
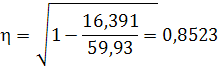
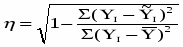
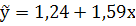
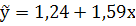
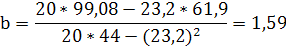
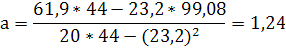
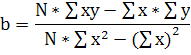
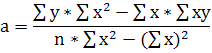
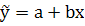
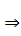
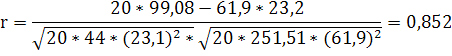
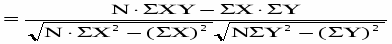
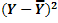
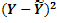
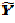 Задача 1
Задача 1
Определить зависимость между фактором и результатирующим признаком по данным, приведенным в таблице. Рассчитать коэффициент корреляции, определить вид зависимости, параметры линии регрессии, корреляционное отношение и оценить точность аппроксимации. Выбор варианта осуществляется по последней цифре порядкового номера студента
Решение:
Построим расчетную таблицу
N
Расходы по эксплуатации машин и механизмов (тыс. ден. ед), X
Основная заработная плата (тыс. ден. ед), Y
XY
X2
Y2
1
3,2
6,3
20,16
10,24
39,69
6,35
0,003
10,27
2
0,5
1,1
0,55
0,25
1,21
2,04
0,886
3,98
3
1,2
2,9
3,48
1,44
8,41
3,16
0,067
0,04
4
0,1
2,5
0,25
0,01
6,25
1,40
1,203
0,35
5
0,5
2,3
1,15
0,25
5,29
2,04
0,067
0,63
6
0,6
4,7
2,82
0,36
22,09
2,20
6,244
2,58
7
0,8
2,5
2
0,64
6,25
2,52
0,000
0,35
8
1,3
3,6
4,68
1,69
12,96
3,32
0,079
0,26
9
2,1
5
10,5
4,41
25
4,60
0,164
3,63
10
0,3
0,7
0,21
0,09
0,49
1,72
1,045
5,74
11
3,2
7
22,4
10,24
49
6,35
0,421
15,25
12
0,5
1
0,5
0,25
1
2,04
1,085
4,39
13
1,4
3,1
4,34
1,96
9,61
3,48
0,143
0,00
14
1,8
2,8
5,04
3,24
7,84
4,12
1,733
0,09
15
0,3
1,4
0,42
0,09
1,96
1,72
0,104
2,87
16
0,4
1
0,4
0,16
1
1,88
0,778
4,39
17
2,3
5,1
11,73
5,29
26,01
4,91
0,034
4,02
18
0,1
2,6
0,26
0,01
6,76
1,40
1,433
0,25
18
1,3
3,8
4,94
1,69
14,44
3,32
0,232
0,50
20
1,3
2,5
3,25
1,69
6,25
3,32
0,670
0,35
сумма
23,2
61,9
99,08
44
251,51
61,9
16,391
59,93
среднее
3,095
Вычислим коэффициент корреляции по формуле:
r
где X и Y- текущие значения наблюдаемых величин;
N- число наблюдений.
Получим:
Коэффициент корреляции лежит в пределах 0 / r / 1 . При положительном коэффициенте корреляции наблюдается прямая связь, т.е. с увеличением независимой переменной увеличивается и зависимая.
В нашем примере r = 0,852 связь тесная
Вычислим уравнение регрессии:
- уравнение регрессии
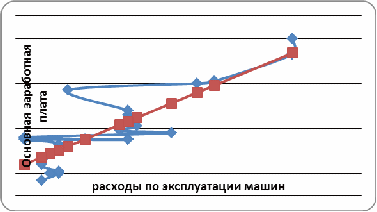
Построим корреляционное поле
Теснота связи для аппроксимации криволинейных зависимостей определяется при помощи корреляционного отношения
r =
Дополнительной оценкой точности аппроксимации является средняя относительная ошибка аппроксимации. Линия регрессии - аппроксимирующая функция. Чем меньше E, тем точнее выбранная зависимость аппроксимирует существующую зависимость
Вычислим точность аппроксимации:
где Yi- наблюденное значение зависимой переменной ;
- рассчитанное по формуле значение;
- среднее значение;
Вывод:
Между факторами имеется тесная связь.
Связь прямая
Прямолинейная зависимость лучше отображает связь.
Задача 2
2.1 По приведенным ниже данным – матрицы прибыли в зависимости от выбранной стратегии и состоянии факторов внешней среды, выбрать наиболее предпочтительную стратегию по критериям Лапласа, Вальда, Гурвица и Сэвиджа.
Состояние факторов внешней среды
1
2
3
4
5
6
А
100
120
130
130
120
110
Б
110
90
150
120
120
100
В
150
150
100
90
100
90
Г
130
100
110
120
120
110
Д
150
110
110
100
130
150
Е
190
90
100
170
120
90
Ж
100
140
140
140
130
100
З
120
150
130
130
120
90
И
140
120
130
120
150
100
Критерий Лапласа.
Критерием выбора стратегии выступает максимизации математического ожидания.
Состояние факторов внешней среды
М
Варианты стратегий
1
2
3
4
5
6
А
100
120
130
130
120
110
118
Б
110
90
150
120
120
100
115
В
150
150
100
90
100
90
113
Г
130
100
110
120
120
110
115
Д
150
110
110
100
130
150
125
Е
190
90
100
170
120
90
127
Ж
100
140
140
140
130
100
125
З
120
150
130
130
120
90
123
И
140
120
130
120
150
100
127
Вывод: В соответствии с критерием Лапласа стратегии СЕ и СИ характеризуются максимальным математическим ожиданием прибыли.
Критерий Вальда
В соответствии с критерием Вальда субъект, принимающий решение, избирает чистую стратегию, гарантирующую ему наибольший (максимальный) вариант из всех наихудших (минимальных) возможных исходов действия по каждой стратегии. На этой основе получается решение, определяемое как
Состояние факторов внешней среды
min
Варианты стратегий
1
2
3
4
5
6
А
100
120
130
130
120
110
100
Б
110
90
150
120
120
100
90
В
150
150
100
90
100
90
90
Г
130
100
110
120
120
110
100
Д
150
110
110
100
130
150
100
Е
190
90
100
170
120
90
90
Ж
100
140
140
140
130
100
100
З
120
150
130
130
120
90
90
И
140
120
130
120
150
100
100
W = 100
Вывод: В соответствии с критерием рекомендуемые стратегии СА, СГ, СД, СЖ, СИ гарантируют максимальный результат (100) в самой неблагоприятной ситуации.
Критерий Гурвица
Согласно критерию Гурвица при выборе решения разумней придерживаться некоторой промежуточной позиции. В соответствии с этим компромиссным критерием для каждого решения определяется линейная комбинация минимального и максимального выигрышей
,
где a- показатель пессимизма-оптимизма, принимающий значения 0 a1,
Вывод: Согласно критерию Гурвица стратегия СЕ обеспечивает максимальное значение линейной комбинации
Критерий Сэвиджа
Чтобы оценить, насколько то или иное состояние природы влияет на исход в соответствии с критерием Сэвиджа вводится показатель риска(r ij), определяемый как разность между максимально возможным выигрышем при данном состоянии (Rj) и выигрышем при выбранной стратегии (Si)
; при ,
где rij - показатель риска;
j - максимально возможный выигрыш;
x ij - выигрыш при выбранной стратегии
На этой основе строят матрицу рисков, которая показывает "сожаление между действительным выбором и наиболее благоприятным, если бы были известны намерения природы". Затем выбирается такая стратегия, при которой величина риска принимает минимальное значение в самой неблагоприятной ситуации
Без риска
С риском
Без риска
С риском
Без риска
С риском
Без риска
С риском
Без риска
С риском
Без риска
С риском
Max rij
1
2
3
4
5
6
А
100
90
120
30
130
20
130
40
120
30
110
40
90
Б
110
80
90
60
150
0
120
50
120
30
100
50
80
В
150
40
150
0
100
50
90
80
100
50
90
60
80
Г
130
70
100
50
110
40
120
50
120
30
110
40
70
Д
150
40
110
40
110
40
100
70
130
20
150
0
70
Е
190
0
90
60
100
50
170
0
120
30
90
40
60
Ж
100
90
140
10
140
10
140
50
130
20
100
50
90
З
120
70
150
0
130
20
130
40
120
30
90
60
70
И
140
50
120
30
130
20
120
50
150
0
100
50
50
мах
190
150
150
170
150
150
S = 50
Вывод: В соответствие с критерием рекомендуемая стратегия СИ, выбирая её в самом худшем случаи наше сожаление не превысит 50.д.ед.
2.2 При заданном распределении состояний факторов внешней среды определить стандартные статистические показатели (среднюю ожидаемую прибыль, дисперсию, коэффициент вариации прибыли) и обосновать выбор стратегии по индивидуальному отношению к риску.
0,2
0,4
0,1
0,2
0,05
0,05
1
2
3
4
5
6
А
100
120
130
130
120
110
Б
110
90
150
120
120
100
В
150
150
100
90
100
90
Г
130
100
110
120
120
110
Д
150
110
110
100
130
150
Е
190
90
100
170
120
90
Ж
100
140
140
140
130
100
З
120
150
130
130
120
90
И
140
120
130
120
150
100
Вычислим среднюю ожидаемую прибыль по формуле:
МА=100*0,2+120*0,4+130*0,1+130*0,2+120*0,05+110*0,05=118,5
МБ=110*0,2+90*0,4+150*0,1+120*0,2+120*0,05+100*0,05=108
МВ=150*0,2+150*0,4+100*01+90*0,2+100*0,05+90*0,05=127,5
МГ=130*0,2+100*0,4+110*0,1+120*0,2+120*0,05+110*0,05=112,5
МД=150*0,2+110*0,4+110*0,1+100*0,2+100*0,05+150*0,05=119
МЕ=190*0,2+90*0,4+100*0,1+170*0,2+120*0,05+90*0,05=128,5
МЖ=100*0,2+140*0,4+140*0,1+140*0,2+130*0,05+100*0,05=129,5
МЗ=120*0,2+150*0,4+130*0,1+130*0,2+120*0,05+90*0,05=133,5
МИ=140*0,2+120*0,4+130*0,1+120*0,2+150*0,05+100*0,05=125,5
Вычислим среднее квадратичное (стандартное) отклонение:
где - стандартное отклонение;
Ax - результат для вероятности Px;
a - среднее ожидаемое значение результата;
Px - вероятность появления этого результата
Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:
,
где - искомый показатель, - среднее квадратичное отклонение, - средняя величина.
1
2
3
4
5
6
м
А
100
120
130
130
120
110
118,5
Б
110
90
150
120
120
100
108
В
150
150
100
90
100
90
127,5
Г
130
100
110
120
120
110
112,5
Д
150
110
110
100
130
150
119
Е
190
90
100
170
120
90
128,5
Ж
100
140
140
140
130
100
129,5
З
120
150
130
130
120
90
133,5
И
140
120
130
120
150
100
125,5
Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность исследуемых значений. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.
Построим таблицу
1
2
3
4
5
6
м
[М-];[М+]
V%
А
100
120
130
130
120
110
118,5
10,61838
[107,88 ;129,12]
8,95
Б
110
90
150
120
120
100
108
18,60108
[89,40 ;126,60]
17,22
В
150
150
100
90
100
90
127,5
27,72634
[99,77 ;155,23]
21,74
Г
130
100
110
120
120
110
112,5
11,77922
[100,72; 124,28]
10,46
Д
150
110
110
100
130
150
119
18,9473
[100,05 ;137,95]
15,92
Е
190
90
100
170
120
90
128,5
43,04358
[85,46 ;171,54]
33,49
Ж
100
140
140
140
130
100
129,5
17,16828
[112,33 ;146,67]
13,25
З
120
150
130
130
120
90
133,5
15,89811
[117,60 ;149,40]
11,9
И
140
120
130
120
150
100
125,5
11,16915
[114,33 ;136,67]
8,9
Вывод: на мой взгляд самая оптимальная стратегия СЕ, т.к во время кризиса мы потеряем много прибыли, но в тоже время в благоприятных условиях мы приобретем много прибыли.

Нравится материал? Поддержи автора!
Ещё документы из категории экономико-математическое моделирование:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ