Логика высказываний

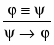
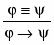
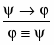
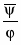
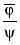
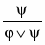
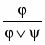
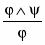
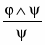
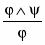
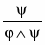
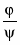
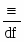
ЛОГИКА ВЫСКАЗЫВАНИЙ
Важнейшей функцией логики является установление того, что из чего следует, а значит установление того, какие формулы являются теоремами, а какие нет. Это достигается с помощью аксиоматического метода. При аксиоматическом построении исчисления высказываний выбирают некоторое, небольшое количество формул, которые включают в систему без доказательства. Это аксиомы системы. Остальные формулы могут быть присоединены к системе только тогда, когда они следуют из аксиом или являются определениями. Существует много эквивалентных систем исчисления высказываний, различающихся аксиомами и исходными терминами. Здесь мы опишем систему Д. Гильберта и В. Аккермана. В исчислении высказываний определение формулы такое же, как и в алгебре высказываний.
В качестве аксиом принимаются следующие четыре высказывания:
р qр
р р q
р q q р
(р q) ( r р r q)
В этой системе принимаются три определения:
Д1 φ ψ ≡φ →ψ
df
______
Д2 φ ψ ≡φψ
df
Д3 (φ ≡ ψ) ≡ (φ →ψ) (ψ →φ)
df
Здесь символ «» означает равносильные по определению.
Для получения новых формул, как из положенных в основу исходных формул, так и из уже выведенных формул, принимаются два правила:
α) Правило подстановки.
Вместо переменного высказывания можно везде, где эта буква встречается, подставить одну и ту же формулу исчисления высказывания.
β) Схема заключения.
Из двух формул φ и φ → ψ получаем новую формулу ψ.
Из сформулированных правил и аксиом можно вывести новые правила вывода формул.
ПРАВИЛО I. Если φ φ – доказуемая формула, то доказуема также формула φ.
Доказательство: Подставим в α) формулу φ. Получим φ φ→ φ. Поскольку φ φ доказуемая формула, то, по правилу β) доказуема и формула φ.
ПРАВИЛО II. Если φ – доказуемая формула, а ψ – любая другая формула, то формула φ ψ является также доказуемой.
Доказательство: Подставим в в) вместо р формулу φ, а вместо q - формулу ψ. Получаем φ φ ψ. Схема заключения дает φ ψ.
ПРАВИЛО III. Если φ ψ – доказуемая формула, то доказуема и формула ψ φ.
Доказательство: Получаем из с) заменой р на φ, q на ψ и применяем схемы заключения.
ПРАВИЛО IV. Если φ→ ψ доказуемая формула, то формула γφ→ γ ψ также доказуема.
Доказательство : Получаем из α) заменой р на φ, q на ψ, r на γ и применяем схемы заключения.
Из аксиом, принятых и выведенных правил можно выводить новые формулы и правила.
Докажем, например, формулу:
(p→q)→((r→p)→(r→q))
Доказательство: Заменим в d) r наr. Получаем (p→q)→ ((rp)→(rq)), но по Д1 эта формула есть иная запись доказываемой формулы.
Доказательство: Подставим в формулу вместо р формулу ψ, вместо q формулу γ, вместо r формулу φ. Получаем: (ψ → γ )→(( φ→ ψ)→( φ→ γ)) .
Применяя два раза схему заключения, получаем: φ→ γ.
Легко доказать, что в предложенной аксиоматической системе выводимы формулы алгебры высказываний. Докажем например, что формула рp выводима.
Доказательство: Подставляем в в) вместо q переменную р , получаем формулу р→ рp. Из а) той же подстановкой получаем рp→ р. По правилу У выводим формулу p→ р. По Д1 эта формула представляет собой иную запись формулырp.
Аналогичным образом можно доказать остальные формулы алгебры высказываний.
Предложенное аксиоматическое исчисление высказываний удовлетворяет всем требованиям аксиоматического метода: система аксиом этого исчисления высказываний полна, независима и противоречива. Доказательство этого факта читатель может найти в любом учебнике по математической логике.
Система исчисления высказываний может быть построена методом допущений. Этот метод ближе к обычным содержательно очевидным представлениям в том отношении, что доказательства в системах, построенных этим методом, почти не отличаются от математических доказательств и от рассуждений в других науках. Здесь оно излагается по книге Е. Слупецкого, Л. Борковского «Элементы математической логики и теории множеств».
В натуральном исчислении высказываний принимается определение формулы алгебры высказываний и следующие правила:
Правило отделения (обозначает ПО):
ПО φ→ ψ
;
Читается эта схема так: «Если в доказательстве имеются уже формула φ→ ψ и формула φ независимо от порядка, в каком эти формулы входят в доказательство, то к доказательству можно присоединить в качестве строки и формулу ψ».
Правило введения конъюнкции
ВК φ
;
Способ чтения этой схемы аналогичен.
Правило удаления конъюнкции:
УК ,
Правило УК можно записать в виде одной схемы:
УК
Ψ
Правило введения дизъюнкции:
ВД ,
Правило удаления дизъюнкции:
УД φ ψ φ ψ
,
Правило введения эквивалентности:
ВЭ φ→ ψ
6)Правило удаления эквивалентности:
УЭ ,
Прямое доказательство выражения φ1 →(φ2→( φ3→ …(φп-1 →φп)…) строится следующим образом:
В первых n-1 строках выписываются последовательно выражения φ1, φ2,… φп-1 в качестве условий теоремы.
К доказательству можно присоединить:
ранее доказанные теоремы в качестве новых строк;
новые строки на основании уже имеющихся строк по правилам ПО, ВК, УК, ВД, УД, ВЭ, УЭ.
Доказательство закончено, если его последняя строка есть выражение φп. Последняя строка доказательства не нумеруется; тем самым отмечается, что доказательство закончено.
Косвенное доказательство выражения φ1 →(φ2→( φ3→ …(φп-1 →φп)…) строится следующим образом:
а) В первых n-1 строках выписываются последовательно выражения φ1, φ2,… φп-1 в качестве условий теоремы.
В n-ой строке выписывается выражениеφп в качестве допущения косвенного доказательства.
К доказательству можно присоединить:
ранее доказанные теоремы в качестве новых строк;
новые строки на основании уже имеющихся строк по правилам ПО, ВК, УК, ВД, УД, ВЭ, УЭ.
Доказательство закончено, если в нем имеются две противоречащие строки. Окончание доказательства отмечается написанием в последней ненумерованной строке выражения «ПРТВРЧ» (сокращение слова «противоречие») с указанием справа номеров двух противоречащих строк.
Продемонстрируем приемы доказательства на ряде примеров. Их мы будем нумеровать с указанием слева Ті ( теорема номер і )
Т1 (Закон гипотетического силлогизма)
(p→q)→(( q → r)→( p→ r))
Доказательство:
p→q
q → r Допущения
р
q ПО : 1,3
r ПО : 2,4
Т2 (Закон контрапозиции)
(p→q)→( q →р) (30)
p→q Допущения
q
p Допущения косвенного доказательства
q ПО : 1,3
ПРТВРч 2,4
Т3 (Второй закон гипотетического силлогизма)
(p→q)( q → r)→( p→ r)
Доказательство:
p→q
q → r Допущения
р
q ПО : 1,3
r ПО : 2,4
Т4 ( Закон экспортации)
(pq → r) →(р→(q → r)) (32)
Доказательство:
pq → r
р Допущения
q
pq ВК : 2,3
r ПО : 2,4
Т5
(p→q)( р → r) →(p→q r) (32 )
Доказательство:
(p→q)( р → r) Допущения
р
p→q УК : 1 q r
р → r
q ПО : 2,3
r ПО : 2,4
q r ВК : 5,6
Докажем теперь аксиомы a), b), c), d):
pq→р
Доказательство:
1) pq Допущения
р УД : 1
р→ pq
Доказательство:
1) p Допущения
рq ВД : 1
pq→ qр
Доказательство:
1) pq Допущения
2) qр Допущения к.д.
ПРТВВРч 1, 2
(р→ q) → (rр→ rq)
Доказательство:
р→ q Допущения
rр
р УД : 2
q ПО : 1, 3
rq ВД : 4
С помощью таблиц истинности можно убедиться, что ПО исключают случаи, когда его применения к истинным посылкам дает ложные результаты.
По определению импликации φ→ ψ ψ есть следствие φ во всех случаях, кроме такого, когда посылка φ истинна, а заключение ψ ложно. Так, что для доказательства того, что ПО позволяет делать из посылок следствия достаточно доказать, что импликация, антицидент которой является конъюнкция посылок, консеквент – вывод, полученный с помощью этого правила, является всегда истинной формулой.
Для ПО составляем формулу:
(φ→ ψ) φ→ ψ.
И с помощью таблицы истинности убеждаемся, что эта формула тождественно истинна
φ
ψ
φ→ ψ
(φ→ ψ) φ
(φ→ ψ) φ→ ψ
0
0
1
0
1
0
1
1
1
1
1
0
0
0
1
1
1
1
1
1
Для ВК : φψ →φ ψ.
Таблица истинности имеет вид
φ
ψ
φψ
φψ →φ ψ
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
1
С помощью таблиц истинности можно убедиться, что и остальные правила натурального исчисления высказываний исключают случаи, когда результат их применение к истинным посылкам был бы ложным. С другой стороны, поскольку конъюнкция посылок ложна, когда хотя бы одна из посылок ложна, то по определению импликации из конъюнкции этих посылок следует любое высказывание как истинное, так и ложное. Следовательно, ложные посылки лишены смысла. Так, что и с формальной, и с содержательной точки зрения правила построения доказательств, по видимому, не должны вызывать сильных возражений.
Литература
Логическое суждение. Руфулаев О.Н. К. – 2005 г.
Логика – исскуство мышления. Тимирязев А.К.– К. 2000 г.
Философия и жизнь – журнал- К. 2004 г.
История логики и мышления – Касинов В.И. 1999.
Логика и человек – М. 2000.
Философия жизни. Матюшенко В.М. – Москва – 2003 г.
Философия бытия. Марикова А.В. – К. 2000 г.

Нравится материал? Поддержи автора!
Ещё документы из категории философия :
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ