ЗАДАНИЕ

Известны следующие данные о доходности капитала компании, уровне дивидендов и ценах акции:

№

Уровень дивидендов, %

Доходность капитала, %

Цена акции, д.е./шт.

1

2,1

20,4

31

2

4,2

27,3

40

3

3,2

32,6

30

4

6,2

25,6

68

5

5,0

15,8

43

6

6,8

29,2

66

7

5,8

30,8

56

8

6,6

24,6

40

9

4,8

26,7

46

10

4,8

25,4

48

11

5,2

30,6

51

12

5,6

30,4

53

13

5,4

24,0

52

14

3,8

30,6

40

15

3,8

27,8

40

16

7,2

46,6

56

17

4,9

31,2

43

18

6,0

30,0

42

19

6,2

22,4

52

20

4,3

24,5

25

Требуется:

1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии.

4. сделать вывод о силе связи результативного показателя с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.

6. Построить поля корреляции результативного показателя и факторов.

По результатам анализа пунктов 1. – 5, выбрать более значимый фактор и для него:

1. Определить параметры а и b уравнения парной линейной регрессии:

2. Линейный коэффициент корреляции.

3. Найти индекс корреляции.

4. На основании полученных двух моделей найти два значения результативного показателя при ожидаемых в среднем значениях х₁ = 7%, х₂ = 32,0%.

7. Сделать выводы.

Задание 1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров

Модель множественной линейной регрессии:

y=a+b1*x1+b2*x2

Коэффициенты уравнения регрессии находятся из системы по МНК:

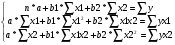
Расчетная таблица

№

Уровень дивидендов, %, х1

Доходность капитала, %, х2

Цена акции, д.е./шт., у

х1*х1

х2*х2

у*у

х1*у

х2*у

х1*х2

1

2,1

20,4

31

4,41

416,16

961

65,1

632,4

42,84

2

4,2

27,3

40

17,64

745,29

1600

168

1092

114,66

3

3,2

32,6

30

10,24

1062,76

900

96

978

104,32

4

6,2

25,6

68

38,44

655,36

4624

421,6

1740,8

158,72

5

5

15,8

43

25

249,64

1849

215

679,4

79

6

6,8

29,2

66

46,24

852,64

4356

448,8

1927,2

198,56

7

5,8

30,8

56

33,64

948,64

3136

324,8

1724,8

178,64

8

6,6

24,6

40

43,56

605,16

1600

264

984

162,36

9

4,8

26,7

46

23,04

712,89

2116

220,8

1228,2

128,16

10

4,8

25,4

48

23,04

645,16

2304

230,4

1219,2

121,92

11

5,2

30,6

51

27,04

936,36

2601

265,2

1560,6

159,12

12

5,6

30,4

53

31,36

924,16

2809

296,8

1611,2

170,24

13

5,4

24

52

29,16

576

2704

280,8

1248

129,6

14

3,8

30,6

40

14,44

936,36

1600

152

1224

116,28

15

3,8

27,8

40

14,44

772,84

1600

152

1112

105,64

16

7,2

46,6

56

51,84

2171,56

3136

403,2

2609,6

335,52

17

4,9

31,2

43

24,01

973,44

1849

210,7

1341,6

152,88

18

6

30

42

36

900

1764

252

1260

180

19

6,2

22,4

52

38,44

501,76

2704

322,4

1164,8

138,88

20

4,3

24,5

25

18,49

600,25

625

107,5

612,5

105,35

Итого

101,9

556,5

922

550,47

16186,4

44838

4897,1

25950,3

2882,69

Среднее

5,095

27,825

46,1

27,5235

809,322

2241,9

244,855

1297,52

144,135

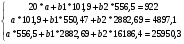
a=13,807

b1=6,391

b2=-0,01

y=13,807+6,391*х1-0,01*x2

При уровня дивидендов на 1 % цена 1 акции увеличивается на 6,391 д.е. При увеличении доходности капитала на 1 % цена 1 акции уменьшается на 0,01 д.е.

Задание 2. Рассчитать частные коэффициенты эластичности

Э(х1)=b1 * 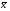/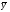=6,391*5,095/46,1=0.706

Э(х2)=b2 * 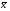/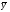=-0,01*27,825/46,1=-0,006

Задание 3. Определите стандартизованные коэффициенты регрессии

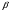= b*/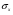

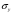
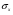- стандартное отклонение факторного признака (х);

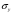- стандартное отклонение результативного признака (у).

,

,

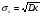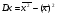
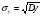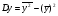
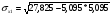=1.251

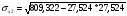=7,194

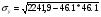=10,802

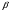(х1)= b1*/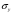=6,391*1,251/10,802=0.74

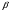(х2)= b2*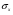/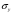=-0,01*7,194/10,802=-0,007

Задание 4. Сделайте вывод о силе связи результативного показателя с каждым из факторов

При неизменной доходности капитала при увеличении уровня дивидендов на 1 процентный пункт (п. п.) ее среднего значения цена акции увеличивается на 0,706 % ее среднего значения; при увеличении уровня дивидендов на 1 сигму цена акции увеличивается на 0,74 сигм.

При неизменном уровне дивидендов при увеличении доходности капитала на 1 п. п. его среднего значения цена акции уменьшается на 0,006 % ее среднего значения; при увеличении доходности капитала на 1 сигму цена акции уменьшается на 0,007 сигм.

Задание 5. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции

Парные коэффициенты корреляции:

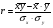
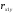=(244,855-5,095*46,1)/(1,251*10,802) = 0,738

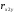=(1297,52-27,825*46,1)/(7,194*10,802)= 0,19

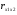=(144,135-5,095*27,825)/(1,251*7,194)=0,263

Частные коэффициенты корреляции:

- чистое влияние на цену акции фактора х1 – уровень дивидендов)

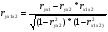
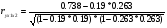=0.726

-чистое влияние на цену акции фактора х2 – доходности капитала

=-0,006

Коэффициент множественной корреляции:

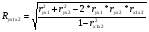
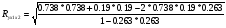= 0.738

Задание 6. Построить поля корреляции результативного показателя и факторов

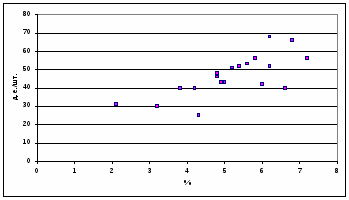
Поле корреляции фактора х1 (уровень дивидендов) и цены акции

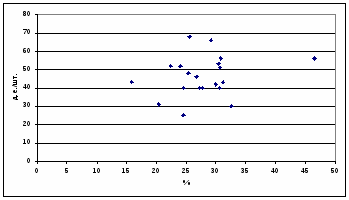
Поле корреляции фактора х2 (доходность капитала) и цены акции

По результатам анализа п. 1-5 выбрать наиболее значимый фактор и для него:

1. определить параметры a и b уравнения парной регрессии

Наиболее значимый фактор х1 ( уровень дивидендов)

Линейная функция: y_х3=a + b*х1. Параметры а и b определяются по способу наименьшим квадратов путем решением следующей системы нормальных уравнений:

,

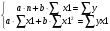Расчетная таблица

№

Уровень дивидендов, %, х1

Цена акции, д.е./шт., у

х1*х1

у*у

х1*у

у(х)

(у(х)-у)^2

(y-cp y)^2

1

2,1

31

4,41

961

65,1

27,0026

15,9792

228,01

2

4,2

40

17,64

1600

168

40,3922

0,15382

37,21

3

3,2

30

10,24

900

96

34,0162

16,1299

259,21

4

6,2

68

38,44

4624

421,6

53,1442

220,695

479,61

5

5

43

25

1849

215

45,493

6,21505

9,61

6

6,8

66

46,24

4356

448,8

56,9698

81,5445

396,01

7

5,8

56

33,64

3136

324,8

50,5938

29,227

98,01

8

6,6

40

43,56

1600

264

55,6946

246,32

37,21

9

4,8

46

23,04

2116

220,8

44,2178

3,17624

0,01

10

4,8

48

23,04

2304

230,4

44,2178

14,305

3,61

11

5,2

51

27,04

2601

265,2

46,7682

17,9081

24,01

12

5,6

53

31,36

2809

296,8

49,3186

13,5527

47,61

13

5,4

52

29,16

2704

280,8

48,0434

15,6547

34,81

14

3,8

40

14,44

1600

152

37,8418

4,65783

37,21

15

3,8

40

14,44

1600

152

37,8418

4,65783

37,21

16

7,2

56

51,84

3136

403,2

59,5202

12,3918

98,01

17

4,9

43

24,01

1849

210,7

44,8554

3,44251

9,61

18

6

42

36

1764

252

51,869

97,3972

16,81

19

6,2

52

38,44

2704

322,4

53,1442

1,30919

34,81

20

4,3

25

18,49

625

107,5

41,0298

256,954

445,21

Итого

101,9

922

550,47

44838

4897,1

921,974

1061,67

2333,8

Среднее

5,095

46,1

27,5235

2241,9

244,855

 -

- 

- 

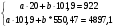
а=13,613

b=6,376

y(x1)=13,613+6,376*x1

2. линейный коэффициент корреляции

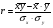
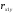=(244,855-5,095*46,1)/(1,251*10,802) = 0,738

3. найти индекс корреляции

Индекс корреляции:

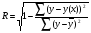
=0,738

4. на основании полученных двух моделей найти два значения результативного показателя при ожидаемых в среднем значениях х1=7%, х2=32%.

Y(х1, х2)=13,807+6,391*х1-0,01*x2

y(7;32)= 13,807+6,391*7-0,01*32 = 58,224 д.е. за штуку

y(x1)=13,613+6,376*x1

y(7)=13,613+6,376*7=58,245 д.е. за штуку

7. Сделать выводы

Цена акции зависит от уровня дивидендов и доходности капитала. Как показали расчеты связь между уровнем дивидендов и ценой акции умеренно-сильная, прямая. Связь между доходностью капитала и ценой акции слабая обратная. Совместное влияние двух факторов может быть оценено как достаточно сильное.

При ожидаемых в среднем значениях уровня дивидендов (7%) и доходности капитала (32%) цена акции будет находится в интервале от 52,22 до 52,25 д.е. за штуку.