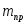
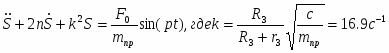
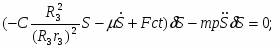
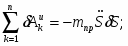
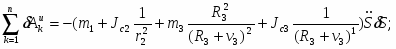
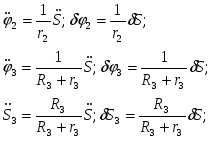
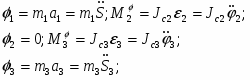
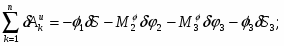
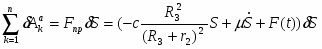
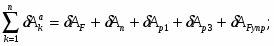
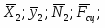
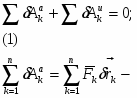
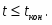
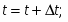
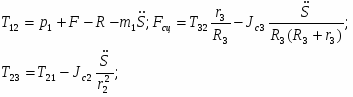
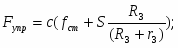
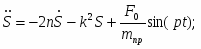
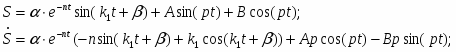
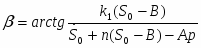
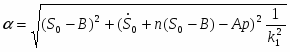
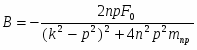
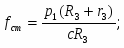
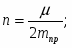
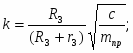
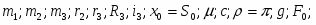
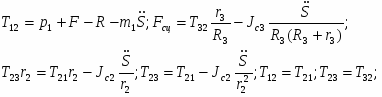
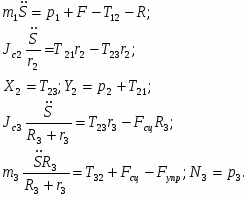
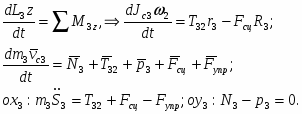
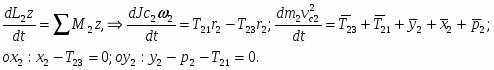
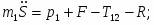
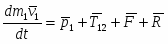
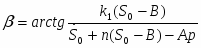
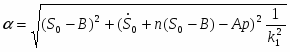
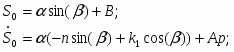
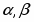
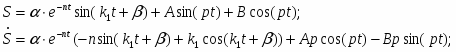
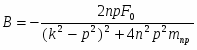
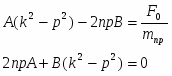
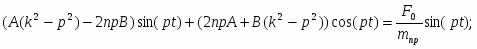
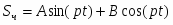
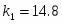
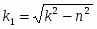
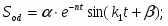
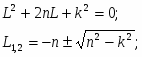
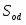
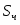
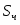
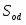
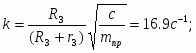
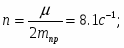
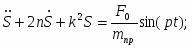
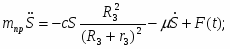
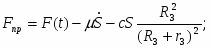
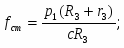
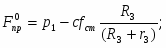
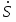
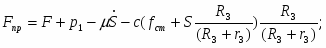
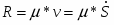
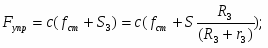
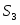
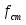
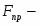
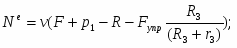
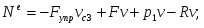
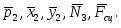
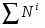
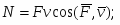
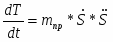
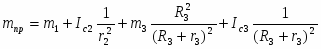
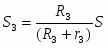
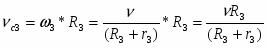
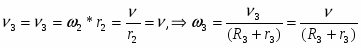
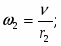
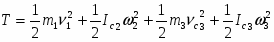
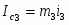
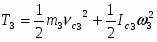
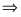
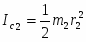
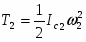
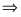
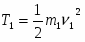
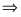
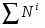
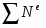
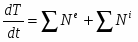
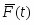
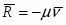
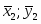
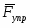
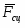
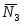
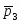
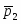
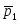
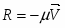
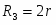
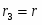
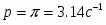
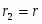
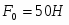
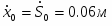
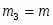
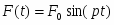
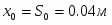
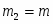
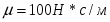
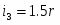
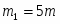
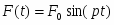
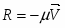Содержание:

Аннотация

Исходные данные

1. Применение основных теорем динамики механической системы

1. Постановка второй основной задачи динамики системы

2. Определение закона движения системы

3. Определение реакций внешних и внутренних связей

2. Построение алгоритма вычислений

3. Применение принципа Даламбера-Лагранжа и уравнений Лагранжа второго рода.

1. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.

Анализ результатов

Аннотация

Дана механическая система с одной степенью свободы, представляющая собой совокупность абсолютно твердых тел, связанных друг с другом посредством невесомых растяжимых нитей, параллельных соответствующим плоскостям. Система снабжена внешней упругой связью с коэффициентом жесткости с. На первое тело системы действует сила сопротивления и возмущающая гармоническая сила . Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Применяя основные теоремы динамики системы и аналитические методы теоретической механики, определен закон движения первого тела и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ.

Исходные данные:

m = 1 кг

r = 0.1 м

с = 4000 H/м

Часть 1. Применение основных теорем динамики механической системы

1.1 Постановка второй основной задачи динамики системы.

Расчетная схема представлена на рисунке 1.

Здесь обозначено:

;- силы тяжести;

- нормальная реакция опорной плоскости;

- сила сцепления;

- упругая реакция пружины;

- реакция подшипников;

- сила вязкого сопротивления;

- возмущающая сила.

Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка (3) происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза (1).

Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:

- сумма мощностей внешних сил;

- сумма мощностей внутренних сил;

Тогда кинетическая энергия системы равна сумме кинетических энергий тел,

(1.2)

(1.3) Груз (1) совершает поступательное движение, ;

(1.4) Блок (2) совершает вращательное движение, , где

(1.5) Каток (3) совершает плоскопараллельное движение, , где

Кинетическая энергия всего механизма равна:

(1.6) ;

Выразим – через скорость груза (1)

(1.7) ;

Подставляя кинематические соотношения (1.7) в выражение (1.6), получаем:

(1.8)

(1.9)

;

Найдем производную от кинетической энергии по времени:

(1.10)

Вычислим сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость в точке ее приложения;

(1.11)

Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемые и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:

(1.12) = 0;

Будут равняться нулю и мощности следующих внешних сил, приложенных в точках, скорости которых равны нулю:

Сумма мощностей остальных внешних сил:

(1.13)

С учетом кинематических соотношений (1.7) сумму мощностей внешних сил определим:

(1.14)

где приведенная сила.

Упругую силу считаем пропорциональной удлинению пружины, которое равно сумме статического и динамического удлинений:

(1.15)

Сила вязкого сопротивления , тогда

(1.16)

В состоянии покоя системы приведенная сила равна нулю. Полагая в (1.16) S=0, =0 и F(t)=0, получаем условие равновесия системы:

(1.17)

Отсюда статическое удлинение пружины равно:

(1.18)

Подставляя (1.18) в (1.16), получаем окончательное выражение для приведенной силы:

(1.19)

Подставив выражения для производной от кинетической энергии и сумму мощностей всех сил с учетом (1.19) в (1.1), получаем дифференциальное уравнение движения системы:

(1.20)

(1.21)

где k циклическая частота свободных колебаний;

n – показатель степени затухания колебаний;

1.2 Определение закона движения системы

Проинтегрируем дифференциальное уравнение (1.20). общее решение этого неоднородного уравнения складывается из общего решения однородного уравнения и частного решения неоднородного :

S = + ;

Однородное дифференциальное уравнение, соответствующее данному неоднородному, имеет вид:

Составим характеристическое уравнение и найдем его корни:

т.к. n < k => решение однородного уравнения имеет вид:

где частное решение дифференциального уравнения ищем в виде правой части:

далее получаем:

Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения состояния А и В

Решая эту систему получаем следующие выражения:

А = 0.04 м;

В = - 0.008 м;

Общее решение дифференциального уравнения:

Постоянные интегрирования определяем из начальных условий, при t = 0 имеем:

Решая эту систему получаем:

3. Определение реакций внешних и внутренних связей

Для решения этой задачи расчленим механизм на отдельные части и изобразим расчетные схемы отдельно для каждого тела. Определение реакций связей проведем с помощью теоремы об изменении кинетического момента и теоремы об изменении количества движения.

Тело №1:

Тело №2:

Тело №3:

C учётом кинематических соотношений (1.7) полученную систему уравнений преобразуем к вид:

Решая эту систему, получаем выражение для определения реакций связей:

2. Построение алгоритма вычислений:

(2.1) Исходные данные:

(2.2) Вычисление констант:

(2.3) Задание начального времени: t=0;

(2.4) Вычисление значений функций в момент времени t=0;

(2.5) Вычисление реакций связей:

(2.6) Вывод на печать значений искомых функций в момент времени t;

(2.7) Определение значения времени на следующем шаге

(2.8) Проверка условия окончания цикла:

(2.9) Возврат к пункту (2.4).

3. Применение принципа Даламбера-Лагранжа и уравнения Лагранжа второго рода

3.1 Применение принципа Даламбера-Лагранжа

Общее уравнение динамике системы есть математическое выражение принципа Даламбера-Лагранжа.

сумма элементарных работ всех активных сил на возможном перемещении системы;

сумма элементарных работ всех инерции сил на возможном перемещении системы.

Изобразим на рисунке активные силы и силы инерции (рис.3)

Идеальные связи:

Не учитываем, и не отображаем на расчетной схеме, поскольку по определению работа их реакций на любом возможном перемещении системы равна 0.

Сообщим системе возможное перемещение.

Вычисляя последовательно элементарные работы активных сил и суммируя получим:

(2)

Найдём возможную работу сил инерции:

Запишем выражение для главных векторов и главных моментов сил инерции;

Используя кинематические соотношения (1.7), определим:

Теперь возможную работу сил инерции можно преобразовать к виду:

(3)

Далее подставляя выражения (2) и (3) в (1), т.е в общее уравнение динамики получаем

Поделив это уравнение на , получим дифференциальное уравнение вынужденных колебаний системы:

Анализ результатов

В данной курсовой работе мы исследовали динамическое поведение механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение движения механической системы получено тремя способами. Во всех случаях коэффициенты , n, k получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей.