Ідеальна оптична система
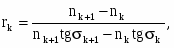
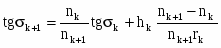
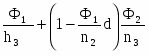

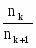
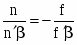
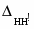

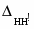
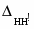
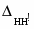
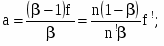
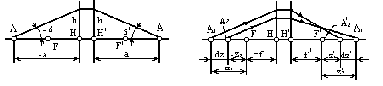
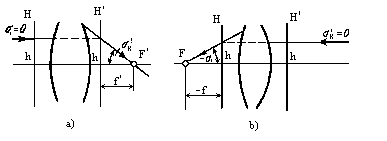
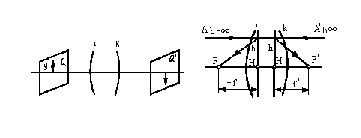
ІДЕАЛЬНА ОПТИЧНА СИСТЕМА
1. Поняття про ідеальну оптичну систему. Кардинальні елементи
Під ідеальною оптичною системою розуміють таку систему, що будь-яку точку простору предметів зображує стигматично, тобто вона не порушує гомоцентричності широких пучків променів, що проходять крізь неї, у межах великої області простору. Теорія ідеальної оптичної системи має чисто геометричний характер. Вона є окремим випадком більш загальної геометричної задачі про перетворення одного простору в інший, котрий називають колінеарним перетворенням. Кожній безлічі точок одного простору відповідає безліч точок в іншому просторі, яке можна назвати зображенням першого. В основі колінеарної відповідності лежать такі розуміння:
- кожній точці простору предметів відповідає тільки одна точка в просторі зображень; ці дві точки є сполученими;
- будь-якій прямій лінії простору предметів відповідає тільки одна сполучена з нею пряма лінія у просторі зображень.
Таким чином, будь-якій площині простору предметів відповідає тільки одна сполучена площина в просторі зображень. У сполучених площинах, що перпендикулярні оптичній осі, зберігається строга подоба.
Виберемо в предметній площині Q, перпендикулярної до осі, предмет у вигляді лінійного відрізка у (рис. 1). Зображенням цього предмета буде відповідний відрізок у'. Відношення розміру зображення до розміру предмета називають лінійним збільшенням ідеальної системи:
= уу.(1)
Для даної пари сполучених площин Q, Q', перпендикулярних до оптичної осі, лінійне збільшення є постійним і не залежить від розміру предмета. Для іншої пари сполучених площин лінійне збільшення матиме інше значення. Якщо < 0, то зображення стосовно предмета буде переверненим, при > 0 - зображення пряме. Лінійне збільшення визначає масштаб зображення. Теорія ідеальної центрованої оптичної системи була розроблена Гаусом, тому її часто називають оптикою Гауса.
Рисунок 1- До знаходження лінійного збільшення оптичної системи
Рисунок 2- Кардинальні точки оптичної системи
Перейдемо до визначення понять кардинальних (основних) елементів ідеальної оптичної системи. Для цього представимо оптичну систему, що складається з ряду поверхонь, у якій l і k (рис. 2) є першою й останньою поверхнями, і розглянемо три характерних положення предметної точки і її зображення.
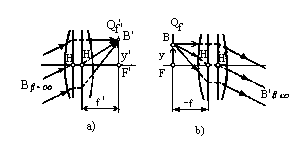
1. Світна точка А знаходиться на оптичній осі в нескінченності. Її зображення буде в точці F', що називають заднім фокусом оптичної системи. Площина, що проходить крізь задній фокус і перпендикулярна оптичній осі, називається задньою фокальною площиною оптичної системи. Ця площина є зображенням нескінченно вилученої площини. Пучок променів, що виходить з нескінченно вилученої точки на оптичній осі, приходить в оптичну систему у вигляді пучка, рівнобіжного оптичній осі. Отже, задній фокус володіє тою властивістю, що крізь нього проходить усякий промінь, що входить в оптичну систему паралельно оптичній осі. Якщо предметна точка В (рис. 3, а), вилучена в нескінченність, знаходиться поза оптичною віссю, то промені, що виходять з цієї точки, утворять похилий пучок рівнобіжних променів. Цей пучок по виходу з оптичної системи збирається в сполученій точці В', що знаходиться поза оптичною віссю, у задній фокальній площині QF.
2. При переміщенні предметної точки А праворуч точка А' (див. рис. 2) переміщатиметься також праворуч і видалиться в нескінченність. У цьому випадку точка А переміститься в точку F. Точку F на оптичній осі в просторі предметів, сполучений з нескінченно вилученою точкою оптичної осі в просторі зображень, називають переднім фокусом оптичної системи. Площина QF, що перпендикулярна оптичній oci і минаює через передній фокус, називають передньою фокальною площиною. Передня фокальна площина сполучена з нескінченно вилученою площиною простору зображень. Отже, пучок променів, що виходить з будь-якої точки В передньої фокальної площини Qp (крім переднього фокуса), виходить із системи похилим пучком рівнобіжних променів (рис. 4, б). Усякий промінь, що входить в оптичну систему через передній фокус, виходить із системи паралельно її оптичної осі.
Рисунок 2- Схема для знаходження властивостей фокальних площин
3. Виберемо пари сполучених і перпендикулярних оптичній осі площини, у яких лінійне збільшення дорівнює плюс одиниці (див. рис. 2). Ці площини називають передньою і задньою головними площинами. Точки їхнього перетинання з оптичною віссю називають передньою Н і задньою Н' головними точками. Тому, що лінійне збільшення в головних площинах дорівнює +1, то будь-який відрізок в одній площині зображується рівним і однаково розташованим відрізком в іншій площині. Звідси випливає, що вхідний і вихідний промені перетинають відповідні головні площини на рівних висотах h.
Відстань HF від передньої головної точки Н до переднього фокуса F є передньою фокусною відстанню оптичної системи, а відстань H'F' від задньої головної точки Н' до заднього фокуса F' - задньою фокусною відстанню. Фокусні відстані позначають відповідно f і f. Їх відраховують від головних точок.
Якщо оптична система знаходиться в однорідному середовищі, наприклад у повітрі (n = n' = 1), то f' = -f, тобто заднє і переднє фокусні відстані рівні за абсолютним значенням. У загальному випадку при n' n
-f/f = n/n'.(2)
Оскільки n > 0 і n' > 0, тo фокусні відстані оптичної системи завжди мають різні знаки. Як правило, для характеристики оптичної системи використовують задню фокусну відстань, тому, якщо f' > 0, то система вважається позитивною, якщо f < 0, то - негативною. У негативних системах задній фокус знаходиться перед оптичною системою.
Рисунок 3- Схема для знаходження фокусних відстаней: а)- заднього, б)- переднього
Фокуси, фокальні площини, головні площини, головні точки і фокусні відстані називають кардинальними елементами оптичної системи.
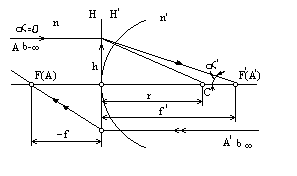
Положення фокусів і головних площин визначають шляхом розрахунку чи графічної побудови ходу променів, паралельних оптичній осі, у прямому і зворотному напрямках (рис. 4). Як випливає з рис. 4, при висоті h падіння променів у прямому і зворотному ході одержуємо такі формули для визначення фокусних відстаней:
f' = h/tgk;
f = h/tg.
2. Залежності між положеннями і розмірами предмета і зображення. Кутове і подовжене збільшення
Уведення кардинальних елементів дозволяє легко визначити положення і розмір зображення графічним способом. Для цього необхідно побудувати хід двох променів, що виходять з однієї позавісьової точки В предмета АВ (рис. 5). Проведемо один промінь паралельно оптичній осі, а інший - крізь передній фокус F. На перетинанні цих променів у просторі зображень буде знаходитиметься зображення В' предметної точки В. З подібності трикутників випливає, що
- у'/у = -f/-z = z'/f.
Звідси можна одержати формулу Ньютона: яку можна одержати, підставивши в (3) z і z', виражені через а й а' згідно з рис. 5.
Відрізки а й а', що визначають положення предмета і зображення щодо відповідних головних площин, знаходяться з формули відрізків:
Рисунок 4- Схема для виводу формули кутового збільшення і формули кутів
Рисунок 5- Схема для знаходження продольного збільшення
zz = ff.(3)
f'/a' + f/a = 1, (4)
При f' = -f формула (4) приймає вигляд
l/a' - l/a = 1/f'. (5)
Лінійне збільшення може бути виражене завдяки відрізкам z, z' і f':
= -f/z = -z/f'. (6)
Якщо у формулі (6) z і z' замінимо на а - f та а' - f', одержимо
(7)
а' = (1 - )f'. (8)
При n = n' відрізок а = (1 - ) f'/.
Якщо відстань між площинами предмета і зображення дорівнює L, а між головними точками , то при заданих L, і у випадку, якщо n = n', матимемо, що
f' = -(L-)/(1-)2; (9)
a' = -(L-)/(1-); (10)
a = -(L-)/(1-). (11)
Лінійне збільшення через відрізки а й а' визначають за формулою
= -fa/f'а = na'/n'a. (12)
Наведені вище формули (3)-(12) при відомих вихідних даних дозволяють знайти положення (відрізки z', а') і розмір зображення (y').
Уведемо поняття ще про два збільшення оптичної системи.
Кутовим збільшенням оптичної системи називають відношення тангенсів кутів, утворених сполученими променями з оптичною віссю:
y = tg '/tg . (13)
З рис. 6 випливає, що
= а/а'. (14)
Використовуючи формули (12) і (14), одержимо, що
= . (15)
Формула (15) установлює зв'язок між кутовим і лінійним збільшеннями.
Точки предмета і зображення, що лежать на оптичній осі, для яких = +1. називаються вузловими точками оптичної системи. З формули (15) видно, що вузлові точки збігаються з головними ( = +1) у тому випадку, якщо оптична система знаходиться в однорідному середовищі. У цьому випадку сполучені промені, що проходять крізь головні точки Н і Н', рівнобіжні один одному.
Подовжнім збільшенням оптичною системою називають відношення розміру зображення нескінченно малого відрізка, розташованого уздовж оптичної осі, до розміру цього відрізка:
= dz'dz.
Продиференціюємо формулу Ньютона (3) по z і z'. Після множення і розподілу знайденого вираження на ff' і заміни відносин z'/f' і f/z через одержимо, що
а = -(f'/f) 2. (16)
На підставі виразів (15) і (16) можна записати:
= -f/f; (17)
= . (18)
Рівняння (18) установлює зв'язок між трьома збільшеннями , і . При f' = -f
= 1; (19)
= 2.(20)
3. Побудова і розрахунок ходу променів крізь ідеальну оптичну систему
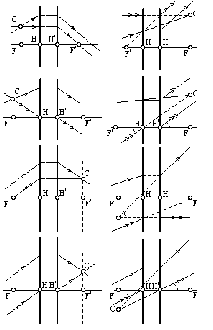
У практичній роботі конструкторів оптичних приладів досить широко використовуються властивості кардинальних елементів і основні математичні залежності ідеальної оптичної системи. Графічне розв’язання задач дозволяє найбільш наочно знайти оптимальний варіант. Чотири способи побудови ходу променів крізь позитивну і негативну оптичні системи зображено на рис. 8. Побудови виконані з припущень, що оптична система розташована в однорідному середовищі, тобто n = n', f = -f, а отже, вузлові N, N' і головні Н, Н' точки збігаються. Дамо деякі пояснення до рис. 8. Точки, загальні для заданого і допоміжного променів у передній фокальній площині, умовно позначені буквою C, а точки, загальні для тих же променів у задній фокальній площині, позначені відповідно через С'. Промені, що виходять із точок C, після проходження системи будуть рівнобіжними між собою. Якщо головні площини зливаються (система тонка), то побудови будуть простіші.
Рисунок 7- Чотири способи побудування ходу променів крізь розташовану в однорідному середовищі оптичної системи
Часто оптичні системи складаються з великого числа окремих компонентів, що вилучений один від одного на значні відстані. У цьому випадку багато задач геометричної оптики зручніше розв’язувати шляхом розрахунку ходу променів. Наприклад, у центрованих оптичних системах положення зображення предмета, перпендикулярного до оптичної осі, можна визначити шляхом розрахунку променя, що проходить крізь вісьову точку А цей предмет. Положення променя, що виходить із точки А і падаючого на висоті h на оптичну систему (див. рис. 6), визначається кутом а з оптичною віссю. Знайдемо кут а'. Згідно з рис. 6 маємо
а = h/tg іа' = h/tg '.
Поставивши а й а' у формулу відрізків (4), після перетворення одержимо
tg ' = (-f/f) tg + hФ/n',
де Ф = n'/f' називають оптичною силою системи.
Останню формулу називають формулою кутів. У загальному вигляді для системи з декількох компонентів вона має такий вигляд:
tg k+1 = (-fk/f'k) tg k + hkФ/nk+1. (21)
У формулі (21) відношення -fk/f можна замінити відношенням показників переломлення, тоді
tg k+1 = tg + hkФk/nk+1 (22)
Якщо оптична система знаходиться в повітрі, то з (22) випливає, що
tg k+1 = tg k + hk Фk. (23)
Висоти h падіння променів на компоненти залежать від кутів, а також від відстаней між цими компонентами:
hk+1 = hk – dk tg k+1. (24)
Рівняння (24) називають формулою висот. Послідовно застосовуючи формули кутів і висот, можна розрахувати хід променів крізь ідеальну оптичну систему будь-якої складності.
4. Багатокомпонентні оптичні системи. Еквівалентна фокусна відстань
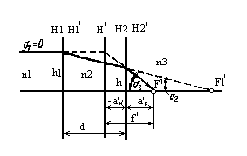
У практиці розрахунку оптичних систем велику роль відіграють двокомпонентні системи (рис. 9). Розглянемо дію такої системи за умови, що фокусні відстані компонентів і їхнє взаємне розташування відомі. Визначити положення фокальних і головних площин системи, що по своїй дії еквівалентна будь-якому числу заданих компонентів, можна шляхом розрахунку променів, рівнобіжних оптичний осі, у прямому і зворотному ході.
Послідовно застосовуючи формули кутів (21) і висот (24) для двокомпонентної системи, одержимо
tg 1 = 0; tg 2 = h1Ф1/n2;
h2 = h1 [1 -(Ф1/n2 )d;
tg = h1 .
Еквівалентна фокусна відстань системи
f = h1/tg 3.
Тоді
Рисунок 8- Система з двох компонентів
n3/f = Ф1 + Ф2 - (Ф1Ф2/n2)d.
Відношення n3/f є оптичною силою Ф усієї системи, тому
Ф = Ф1 + Ф2 - (Ф1Ф2/n2)d. (25)
Відстань від другого компонента до еквівалентного заднього фокуса системи а'F = h3/tg3, або
АF' = f1-(Ф1/n2 )d, (26)
а відстань від цього компонента до задньої головної площини системи
аH = а'F - f. (27)
З розрахунку ходу променя в зворотному ході, тобто з права на ліво, відповідно до формул (21) і (24) одержимо, що
-n/f = Ф = Ф1 + Ф2 – (Ф1Ф2/n2)d;
aF = f(1 - (Ф2/n2)d); (28)
aH = aF – f.
Якщо обидва компоненти оптичної системи знаходяться в однорідному середовищі, наприклад у повітрі, то
Ф = -1/f = 1/f = Ф1 + Ф2 – Ф1Ф2d;
aF = f(1- Ф2d);
aH = aF - f;(29)
аF = f' (1 – Ф1d);
aH = aF - f.
Для трикомпонентної системи, усі компоненти якої знаходяться в повітрі, еквівалентну оптичну силу Ф і відрізок аF- визначають за такими формулами:
Ф = Ф1 + Ф2 + Фз - (Ф2 + Фз) Ф1d1 - (Ф1 + Ф2 - Ф1Ф2d1) Ф3d2;
a'F = (1/Ф) [1 – Ф1 (d1 + d2) – Ф2d2 (1 – Ф1d1)].
Якщо в розглянутій системі компонента стикаються (d1 = d2 = 0), то оптична сила
Ф = Ф1 + Ф2 + Фз,
а відрізок аF дорівнює еквівалентній фокусній відстані системи f'.
Знайти параметри еквівалентної системи можна графічно шляхом побудови ходу променя, рівнобіжного оптичній осі, у прямому і зворотному напрямках.
5. Параксіальна область оптичної системи. Параксіальні і нульові промені
Реальні оптичні системи, що складаються зі сферичних і плоских заломлюючих і поверхонь, що відбивають, у загальному випадку не дають стигматичних зображень, тобто не задовольняють положенням ідеальної оптичної системи, Замість точкових зображень виходять кола розсіювання, Гомоцентричність пучка променів зберігається тільки за умови, що кути і , утворені реальними променями з оптичною віссю і з нормаллю до поверхні, нескінченно малі. При нескінченно малих кутах , , а отже, і ', ' справедливі такі вирази:
sin /sin ' s/s' = s'/s const; (30)
для сферичної заломлюючої поверхні
n'/s' - n/s = (n' - n)/r: (31)
для плоскої заломлюючої поверхні
n'/s' - n/s = 0;(32)
для сферичної поверхні, що відбиває
l/s' + 1/s = 2/r. (33)
У виразах (30)-(33) відрізки s і s' визначають відповідно положення осьової предметної точки і її зображення щодо поверхні. Як видно з (30)-(33), відрізок s' залишається постійним для заданого відрізка s, тобто всі промені, що виходять із предметної точки під будь-якими, але малими кутами, після переломлення перетинаються в одній точці - точці зображення. Промені, що утворять малі кути і ' з оптичною віссю і малі кути й ' з нормаллю до заломлюючої поверхні, називають параксіальними променями, а область біля осі, усередині якої поширюються ці промені, - параксіальною областю. Кути і ' для параксіальної області позначають і '. Співвідношення (31)-(38) називають рівняннями параксіальних променів і використовують для розрахунку ходу променів.
Для зручності виконання розрахунків вводиться поняття нульових променів. Нульовим променем називають фіктивний промінь, що переломлюється (віддзеркалюваний) так само, як і параксіальний, на поверхнях, але зустрічається з ними на кінцевих відстанях від оптичної осі і відтинає на оптичній осі ті ж відрізки, що і параксіальний промінь.
Шляхом розрахунку ходу нульового променя через оптичну систему визначають фокусні відстані і фокальні відрізки, а також положення зображення і лінійне збільшення системи для випадку, коли предмет знаходиться на кінцевій відстані.
Формули для розрахунку ходу нульового променя:
; (34)
1hk+1= hk – dk tg k+.1
З виразу (34) одержимо формулу радіуса:
яку використовують для обчислення радіусів поверхонь при заданому ході променя. Для спрощення написання у формулах (34), (35) tg рекомендується заміняти .
6. Положення головних площин. Фокусні відстані заломлюючої поверхні в параксіальній області
У параксіальній області для реальних центрованих оптичних систем справедливі усі формули і положення ідеальної оптичної системи. Представимо малий предмет як би накладеним на поверхню в її вершини. Очевидно, що зображення цього предмета по положенню і розміру збігається із самим предметом. Отже, у вершині поверхні О (рис. 10) знаходиться сполучена пара сполучених точок, лінійне збільшення в який дорівнює одиниці, тобто, тут знаходяться співпадаючі головні точки заломлюючої поверхні. Головні площини збігаються і лежать у площині, дотичної до сфери в точці 0. Якщо предметну точку А переміщати уздовж оптичної осі так, щоб вона вилучилася в нескінченність, то точка А' збігається з заднім фокусом F' заломлюючої поверхні, тобто
s = -; s' = f'. (36)
Підставивши (36) у (31) і розв’язавши отриманий вираз відносно f', одержимо формулу для визначення задньої фокусної відстані заломлюючої поверхні:
f' = n'r/(n' - n). (37)
Рисунок 9- Схема для знаходження фокусних відстаней сферичної поверхні радіусом r
При переміщенні точки А' уздовж осі в нескінченність сполучена точка А збігається з переднім фокусом F поверхні, тобто
s = f;s' = . (38)
З огляду на вираз (38), з формули (31) знайдемо вираз для передньої фокусної відстані сферичної поверхні:
f = nr/(n'- п). (39)
Розділивши (37) на (39), одержимо
f'/f = n'/n.(40)
Цей важливий вираз записано тут для однієї заломлюючої поверхні, але воно справедливо і для будь-якої складної оптичної системи.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ