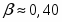
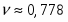
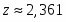
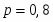
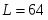
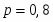
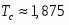
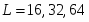
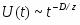
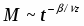
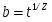
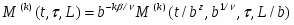
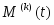
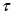
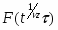
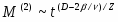
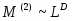
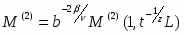
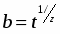
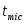
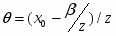
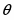
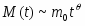
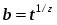
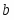
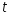
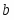
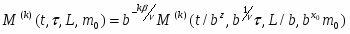
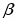
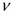
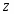
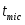
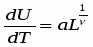
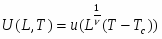
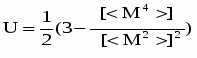
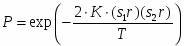
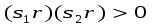
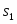
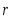
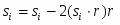
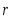
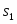
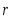
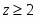
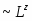
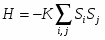
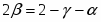
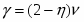
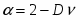
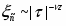
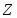
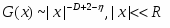
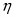
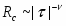
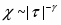
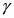
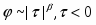
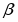
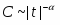
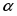
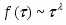
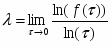
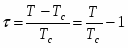
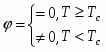МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ФИЗИКИ

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

Исследование влияния линейных дефектов структуры на критическое поведение трехмерной модели Гейзенберга

на степень бакалавра прикладных математики и физики

Направление 511600 - Прикладные математика и физика

Заведующий кафедрой:

профессор В.В. Прудников

Научный руководитель:

профессор В.В. Прудников

Омск - 2010

Оглавление

Введение

Глава 1. Фазовые переходы второго рода, компьютерное моделирование критического поведения

1.1 Фазовые переходы второго рода. Критическое поведение

1.2 Влияние дефектов структуры на критическое поведение

1.3 Теоретическая модель и алгоритмы компьютерного моделирования

1.3.1 Модель Гейзенберга

1.3.2 Алгоритм Вульфа

1.3.3 Метод коротковременной динамики

Глава 2. Результаты моделирования критического поведения трехмерной модели Гейзенберга с линейными дефектами

2.1 Алгоритм Вульфа. Определение критической температуры

2.2 Метод коротковременной динамики. Уточнение критической температуры. Расчет критических индексов

Заключение

Список литературы

Введение

Развитие вычислительных машин открыло новую область теоретической физики - компьютерное моделирование. Это позволяет исследовать поведение различных физических систем, описание которых традиционным способом громоздко или невозможно.

В настоящее время построенная теория упорядоченных конденсированных сред существенно использует идеальность их структуры и не может быть перенесена без существенных изменений на структурно неупорядоченные системы, к которым относятся: кристаллы с примесями, сплавы, аморфные тела и др. Реальные макроскопические системы всегда содержат дефекты структуры. Важнейшими из задач остаются разработка теоретических моделей для описания поведения неупорядоченных систем и исследование их свойств экспериментальным путём.

В данной работе исследуется критическое поведение ферромагнетика с примесями немагнитных атомов в виде случайно распределенных линий, т.е. с дефектами, обладающими квазидальним порядком (корреляционная функция распределения немагнитных атомов убывает по степенному закону G (r) ~ | r |-a с показателем a=2).

В работе [1] проведено теоретико-полевое исследование критического поведения трехмерных систем с дальней пространственной корреляцией дефектов. В ней показано, что дефекты, обладающие свойством дальней пространственной корреляции, изменяют критическое поведение не только систем с однокомпонентным параметром порядка, но и систем с двухкомпонентным (XY-модель) и трехкомпонентным (Гейзенберговская модель) параметром порядка.

Данная работа посвящена моделированию критического поведения трехмерной модели Гейзенберга с линейными дефектами. Основной целью ставилась разработка алгоритмов Метрополиса и Вольфа для данной модели, а затем определение критической температуры перехода в ферромагнитное состояние, и численное определение критических индексов характеризующих основные особенности данных неупорядоченных систем.

Глава 1. Фазовые переходы второго рода, компьютерное моделирование критического поведения

1.1 Фазовые переходы второго рода. Критическое поведение

Фазой называется физически однородная часть системы, отличающаяся своими физическими свойствами от других ее частей и отделённая от них четко выраженной границей [2]. Фазовый переход - это, соответственно, процесс перехода системы из одной фазы в другую. Различают фазовые переходы 1-го и 2-го рода. Основной особенностью фазовых переходов второго рода является непрерывное изменение при переходе плотности и внутренней энергии, внутренняя энергия и плотность вещества - первые производные химического потенциала, но при этом терпят разрыв теплоемкость и восприимчивость - вторые производные химического потенциала. При фазовом переходе второго рода происходит резкое нарушение симметрии системы, т.е. из высоко симметричной фазы в области высоких температур, система при охлаждении переходит в фазу с низкой симметрией.

Для количественной характеристики фазовых переходов второго рода вводят понятие параметра порядка [2]. Параметром порядка называется любая макроскопическая величина, зависящая от температуры следующим образом:

где Tc - температура фазового перехода.

В точке фазового перехода аномально возрастают флуктуации параметра порядка. Для выяснения характера флуктуаций вводят корреляционную функцию флуктуаций параметра порядка G, и величину, называемую корреляционной длиной . При приближении к критической точке корреляционная длина растет и в этой точке становится бесконечной. Крупномасштабные флуктуации приводят к сингулярностям в наблюдаемых макроскопических характеристиках системы.

Для характеристики макроскопических параметров системы, терпящих разрыв при температуре T= Tc, вводят понятие критических индексов, описывающих поведение величин вблизи критической точки [3]. Дадим общее определение критического показателя, описывающего поведение некоторой функции f () вблизи критической точки.

Здесь  - безразмерная переменная, измеряющая степень удаления температуры от критической. Предположим, что функция f () положительна и непрерывна для достаточно малых положительных значений, а также, что существует предел:

Этот предел, обозначенный буквой , получил название критического показателя степени (или просто критического показателя), связанного с функцией f (). Для краткости можно писать , чтобы подчеркнуть тот факт, что  критический показатель функции f (). Критический показатель, конечно, дает значительно меньшую информацию, чем вид полной функции, но вблизи критической точки поведение функции, имеющей вид многочлена, определяют главным образом ее ведущие члены. Поэтому логарифмические кривые, полученные из эксперимента при температурах, достаточно близких к критической точке, имеют вид прямых, и критический показатель легко найти из наклона этих прямых. Таким образом, критические показатели всегда измеримы, чего нельзя сказать о полной функции. Вторая причина такого внимания к критическим показателям заключается в том, что имеется большое число соотношений между критическими показателями, которые выводятся из общих термодинамических и статистических положений, и поэтому справедливы для любой частной системы. Существует простая однозначная связь между критическим показателем и качественным поведением рассматриваемой функции вблизи критической точки =0. Если критический показатель  отрицателен, то соответствующая функция f () вблизи критической точки расходится к бесконечности; положительные же значения  соответствуют функции f (), обращающейся в этой точке в нуль. Чем меньше , тем “резче” поведение f () в том смысле, что для отрицательных  расходимость становится сильнее, а для положительных  кривая идет к нулю более круто.

Итак, для характеристики макроскопических параметров системы вводятся:

критический индекс , характеризующий поведение теплоемкости вблизи критической температуры:

индекс , для параметра порядка

индексы , характеризующие поведение восприимчивости:

индексы ν для характеристики корреляционной длины:

индекс для корреляционной функции:

где D - размерность системы.

Можно ввести динамический критический индекс для описания поведения времени корреляций:

В действительности, не все перечисленные выше критические индексы являются независимыми. Между ними существуют следующие простые соотношения:

Таким образом, чтобы полностью описать критической поведение системы в равновесии, достаточно вычислить лишь какие-либо два статических критических индекса, а оставшиеся легко выражаются через них. Для описания динамики системы необходимо знать индекс z.

гейзенберг фазовый переход критический

1.2 Влияние дефектов структуры на критическое поведение

Реальные макроскопические системы всегда содержат дефекты структуры, например, в ферромагнитном кристалле часть ячеек может быть занята атомами, имеющими нулевой магнитный момент. Если концентрация этих атомов превышает определенную величину, ферромагнетизм полностью подавляется. Другим примером служит ситуация, когда в решетке существуют дефекты, приводящие к случайно распределенным выделенным направлениям ориентации спинов. Несмотря на это, вплоть до сравнительно недавнего времени объектами теории твердых тел были в основном свойства идеальных кристаллических систем, описание которых упрощалось благодаря симметрии решетки относительно трансляций и преобразований соответствующей точечной группы симметрии (вращений, отражений, инверсии). Построенная теория упорядоченных конденсированных сред существенно использует идеальность их структуры и не может быть перенесена без существенных изменений на неупорядоченные системы, к которым относятся: кристаллы с примесями, сплавы, аморфные тела и др.

Современная теория классифицирует примеси в зависимости от их распределения на расплавленные и замороженные. Примеси называют расплавленными, если они находятся в термодинамическом равновесии с исходным веществом. Примеси называют замороженными, если их можно рассматривать как фиксированные в некоторых положениях с распределением, обусловленным способом их внедрения в исходное вещество.

Рассмотрим влияние примесей на критическое поведение. Пусть в систему, находящуюся вблизи критической точки, ввели несколько примесей, включив тем самым малое возмущение. Отклик системы на это возмущение отражается на поведении восприимчивости и корреляционных функций. Вблизи критической точки некоторые из этих величин велики и представляют собой сингулярные функции температуры. Следовательно, малое количество примесей может привести к большим эффектам вблизи критической точки, тем самым изменяя критическое поведение системы. Корреляционная длина, описывающая упорядоченность спинов, начинает зависеть от нового параметра - среднего расстояния между примесями, она как бы рассеивается на дефектах. В результате фазовый переход 2-го рода размывается.

Узнать, влияет ли беспорядок на критическое поведение, помогает критерий Харриса. Так, в случае беспорядка с короткой пространственной корреляцией критическое поведение изменяется, если соответствующий чистой системе критический индекс α_pure, характеризующий поведение теплоемкости, не отрицателен, т.е. α_pure ≥ 0. Этот критерий выполняется только для изинговских систем, с одной спиновой степенью свободы. Точечные дефекты не оказывают влияния на критическое поведение многокомпонентных систем.

В случае беспорядка с квазидальней пространственной корреляцией, задаваемой корреляционной функцией g (x) ~ |x|^-a, справедлив расширенный критерий Харриса - беспорядок влияет, если выполнено условие:

2/a > ν _pure.

Когда атомы примеси образуют линейные дефекты, параметр корреляции дефектов a=2. В результате, для систем с линейными дефектами этот критерий выполняется для многокомпонентных систем - XY-модели и модели Гейзенберга. Следовательно, для определения характеристик критического поведения трехмерной модели Гейзенберга с линейными дефектами требуются дополнительные исследования.

1.3 Теоретическая модель и алгоритмы компьютерного моделирования

1.3.1 Модель Гейзенберга

В данной работе рассматривалась система с гамильтонианом вида:

где сумма берется по всем ближайшим соседям. Спины имеют три степени свободы.

Рассматривалась простая кубическая решетка линейных размеров L с периодичными граничными условиями.

При моделировании мы пользовались следующим методом, позволяющим создавать систему с дальнодействующими корреляциями дефектов: из заполненной трехмерной решетки "вычеркиваются" линии, параллельные осям координат, до достижения заданной концентрации примесей p. Чтобы кристалл был изотропен число вычеркнутых линий в каждом направлении равно. Кроме того налагается условие непересекаемости этих линий, что позволяет гарантировать существование в системе единого протекающего спинового кластера (при концентрации спинов (1-p) >p_c выше порога спиновой перколяции). Это в свою очередь приводит к удалению "шума" от спинов кластеров конечного размера не дающих вклада в магнитные характеристики кристалла.

1.3.2 Алгоритм Вульфа

Традиционное моделирование систем взаимодействующих частиц методом Монте-Карло [4] для изучения их критического поведения наталкивается на трудности [5], связанные в основном с явлением критического замедления, потому что время корреляции, как и время релаксации, ведут себя , где . Т.е. в окрестности критической точки времена релаксации и корреляции возрастают, что приводит к существенному увеличению машинного времени, необходимого на расчет интересующих нас величин.

Поэтому моделирование системы проводилось в два этапа. На первом этапе использовался кластерный алгоритм Вольфа, для определения критической температуры, а затем в ее вблизи исследовалась коротковременная динамика системы.

В работе использовался модифицированный для трехмерной системы кластерный алгоритм Вульфа [6].

1. Выбирается случайный единичный вектор

2. Случайным образом выбираются координаты центрального спина

3. Выбранный спин зеркально отражается в плоскости перпендикулярной направлению :

4. Рассматриваются все соседи данного спина. Спин считается сонаправленным, если он лежат по одну сторону от плоскости перпендикулярной направлению с вектором . Т.е. если

5. Такой спин переворачивается (включается в кластер) с вероятностью

.

6. Если спин перевернут, то аналогичным образом рассматриваются его соседи. Иначе переходим к следующему.

7. На один шаг моделирования может приходиться несколько переворотов кластера.

Алгоритм Вольфа позволяет значительно уменьшить эффекты критического замедления времени релаксации системы.

Для нахождения критической температуры в данной работе рассматривались кумулянты Биндера четвертого порядка. Выражение для кумулянта можно представить в виде:

Где скобки <…> означают статистическое усреднение, а скобки […] - усреднение по различным примесным конфигурациям. Кумулянт U (L,T) имеет важную для описания поведения конечных систем скейлинговую форму:

.

Кумулянт определен так, что 0  U  1. При этом для температур выше T_c U (L,T)  0 в пределе L  . Данная скейлинговая зависимость кумулянта позволяет определить критическую температуру T_c (L=) для бесконечной системы через координату точки пересечения кривых, задающих температурную зависимость U (L,T) для различных L. Более того, легко показать, что в критической области при T Tc

и, следовательно, по максимальному наклону кумулянтов вблизи точки их пересечения при L можно определить значение критического индекса , характеризующего температурную расходимость корреляционной длины при T  Tc.

Применение кумулянтов позволяет хорошо тестировать тип фазового перехода в системе. Так, в случае фазовых переходов второго рода кривые температурной зависимости кумулянтов имеют ярко выраженную зависимость от L и некоторую область (треугольник) пересечения, близкую к точке. В случае фазового перехода первого рода кривые кумулянтов имеют специфический вид без взаимного пересечения, практически отсутствует их зависимость от размера моделируемой системы, а кумулянты в некоторой области температур принимают отрицательные значения.

1.3.3 Метод коротковременной динамики

Традиционно полагалось, что универсальное поведение существует только в равновесии. Однако недавние исследования в критической динамике для многих статических моделей показали, что универсальность также появляется в пределах микроскопического масштаба времени . Исследование метода коротковременной динамики не только показало существование универсального динамического поведения в пределах коротковременного периода, но также дало очень эффективный метод определения критических индексов [7]. Т.о. мы можем оценивать не только динамический критический показатель , но также и статические критические индексы и . Что более важно, результаты находятся в хорошем соответствии с полученными результатами традиционными методами, выполненными в равновесии.

Аналогично измерениям критических индексов определение критических температур также трудно в равновесии из-за критического замедления. Методом коротковременной динамики критическая температура может быть также получена из поведения намагниченности в критической области.

Главным образом из-за большой длины корреляции в равновесном состоянии существует динамическая скейлинговая форма, имеющая силу не только в равновесии, но также в раннем периоде развития критической системы, если система изначально имеет температуру выше критической, а также маленькую намагниченность. Т.о. после микроскопического времени существует скейлинговая форма. В общем случае для момента намагниченности:

.

Здесь - произвольный фактор, - время, - новый независимый критический параметр.

В ранней стадии развития системы длина корреляции мала, и эффекты конечности размеров почти отсутствуют. Выбирая фактор так, чтобы главная зависимость от времени была отменена (т.е. ), в критической точке получим:

,

где - новый динамический индекс, который характеризует универсальность в коротковременной динамике и равен:

.

Отсюда видно, что в течении микроскопического времени , намагниченность подвергается начальному увеличению в критической точке и можно легко получить значения индекса , основываясь на этой степенной форме.

Аналогично, полагая , в критической точке получим поведение второго момента намагниченности:

.

Для второго момента намагниченности можно ожидать, ввиду того, что длина корреляции мала в области ранней стадии развития системы :

.

Вблизи критической температуры в поведении намагниченности возникает дополнительный множитель - скейлинговая функция , т.е. появляются исправление к простому степенному закону, зависящие от . Поэтому при моделировании системы при температуре вблизи критической получается поведение с несовершенным степенным поведением, и критическая температура может быть получена путем интерполирования.

С другой стороны, можно также рассматривать динамические процессы, с начальным состоянием, в котором все спины направлены вверх. Моделирование методами Монте-Карло этих систем показало, что там также существует подобное скейлинговое выражение:

При критической температуре и при , получаем степенной закон для намагниченности:

Конечномерный скейлинговый анализ показывает, что поведение кумулянта Биндера определяется законом:

.

Т.о., появляется возможность измерять критические индексы и определять критическую точку. Критическое замедление почти отсутствует, так как длина корреляции еще маленькая (в течении времени, когда система еще не достигла равновесия). Метод коротковременной динамики может, кроме того, использоваться, как инструмент для отличия фазовых переходов первого рода от второго, сравнивая критическую температуру, полученную от различных стартовых состояний.

Глава 2. Результаты моделирования критического поведения трехмерной модели Гейзенберга с линейными дефектами

2.1 Алгоритм Вульфа. Определение критической температуры

В первой части данной работы использовался алгоритм моделирования Вольфа, с целью уменьшения влияния эффектов критического замедления времени релаксации системы на результаты моделирования. Алгоритм Вольфа характеризуется тем, что на решетке произвольно выбирается спин, строится "физический" кластер, которому этот спин принадлежит, а затем весь построенный кластер переворачивается.

В самом начале вычислений термодинамических характеристик для каждой примесной конфигурации все спины ориентировались в одном направлении (так называемый "холодный старт" - соответствует состоянию системы при Т = 0). Затем чтобы получить конфигурацию спинов, характерную для данной температуры, переворачивалось некоторое количество кластеров. Этот процесс называется термолизацией. В наших вычислениях термолизация составляла 200 шагов Монте-Карло. При этом Монте-Карло шагу соответствовало 5 переворотов кластера Вольфа.

После этого усреднением по N=2000 шагов Монте-Карло вычислялись кумулянты Биндера Результаты усреднялись по 15 - 20 различным реализациям пространственного распределения линейных дефектов образце (примесным конфигурациям). Концентрация спинов выбиралась равной 0.80.

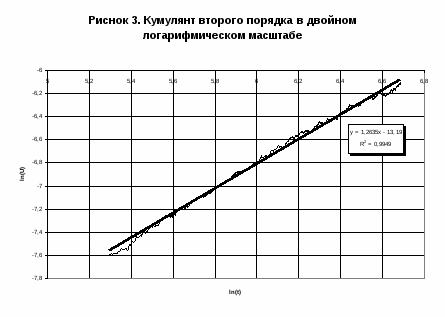
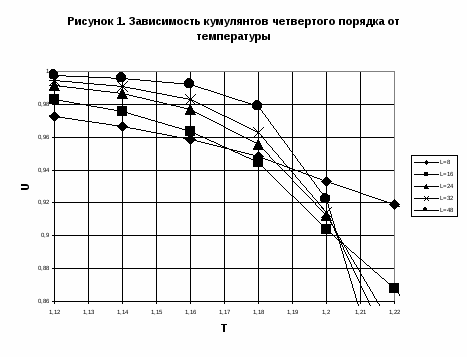
На рис.1 показана температурная зависимость кумулянтов Биндера для различных L. Для разбавленной системы кумулянты пересеклись в области T = 1.20 - 1.21.

2.2 Метод коротковременной динамики. Уточнение критической температуры. Расчет критических индексов

Во второй части работы был реализован метод коротковременной динамики для уточнения критической температуры и вычисления критических показателей. В начальном состоянии все спины были ориентированы в одном направлении, затем использовался алгоритм Метрополиса для нахождения зависимости намагниченности, её логарифмической производной по температуре и кумулянта Биндера от времени. Все вышеуказанные величины усреднялись по примесным конфигурациям.

При моделировании рассматривалась динамика системы в интервале до 1000 шагов Монте-Карло на спин (МКС), около 80 различных конфигураций примесей, для каждой конфигурации проводилось усреднение по 10 прогонкам. Для модели с дальней пространственной корреляцией дефектов характерна сильные флуктуации результатов при малых размерах решетки (L~ 16 - 32). Поэтому в данной работе была предпринята попытка выполнить моделирование для кубической решетки с линейным размером L=64.

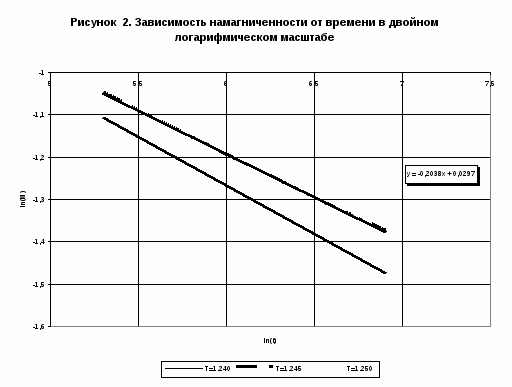
При моделировании получилось, что наилучшим образом удовлетворяет степенному закону поведение намагниченности системы при температуре T=1.245, хотя моделирование методом Вульфа показало, что значение критической температуры должно лежать в пределах 1.20 - 1.21. Несоответствие критических температур, определенных этими двумя методами может быть объяснено недостаточной статистикой результатов и малыми размерами систем, используемыми при методе кумулянтов Биндера.

В табл.1 представлены полученные в данной работе значения критических индексов и критические индексы, полученные в работе [1] теоретико-полевыми методами.

Таблица 1. Критические индексы для модели Гейзенберга с линейно коррелированными дефектами. Концентрация примесей 0.2

Индекс

Результат моделирования

Теоретическое значение [1]

z

2.46  0.12

2.26

β/ν

0.49  0.03

0.48

Найденные значения динамического и статических критических индексов, описывающие критическое поведение трехмерной Гейзенберговской-модели с линейными дефектами, в пределах погрешностей находятся в удовлетворительном согласии с результатами теоретической работы Ошибка: источник перекрестной ссылки не найден. Следует отметить, недостаточное число примесных конфигурации, используемых в работе для усреднения и получения более достоверных значений термодинамических и корреляционных функций. Требуется провести дальнейшее уточнение результатов для данной модели. Тем не менее, результаты проведенных исследований подтверждают факт влияния дальней пространственной корреляции дефектов на критическое поведение трехмерной Гейзенберговской модели (имеющей трехкомпонентный параметр порядка).

Заключение

В данной работе методами компьютерного моделирования было осуществлено исследование влияния эффектов дальней пространственной корреляции немагнитных атомов примеси, распределенных в образцах в виде линейных дефектов структуры, на критическое поведение трехмерной модели Гейзенберга с трехкомпонентным параметром порядка.

Основными результатами работы являются следующие:

1. Для трехмерной модели Гейзенберга были реализованы основные алгоритмы моделирования методом Монте-Карло - алгоритм Метрополиса и кластерный алгоритм Вольфа.

2. В результате применения кластерного алгоритма Вольфа было проведено исследование температурного поведения кумулянтов Биндера 4-го порядка для решеток с размерами . Температуры точек пересечения кумулянтов Биндера для данных решеток позволили определить критическую температуру фазового перехода в ферромагнитное состояние для трехмерной модели Гейзенберга с линейными дефектами со спиновой концентрацией .

3. С помощью метода коротковременной динамики были исследованы зависимости намагниченности, кумулянта Биндера 2-го порядка от времени для размера решетки была уточнена критическая температура системы (). Для трехмерной модели Гейзенберга с линейными дефектами со спиновой концентрацией из временных зависимостей указанных выше величин были получены значения динамического и статических критических индексов: , и , соответственно.

Найденные значения динамического и статических критических индексов, описывающие критическое поведение трехмерной модели Гейзенберга с линейными дефектами, в пределах погрешностей находятся в удовлетворительном согласии с результатами теоретической работы Ошибка: источник перекрестной ссылки не найден. Можно сделать вывод, что факт влияния дальней пространственной корреляции дефектов на критическое поведение трехмерной модели Гейзенберга подтверждается.

Список литературы

1.V. V. Prudnikov, P. V. Prudnikov, A. A. Fedorenko Field-theory approach to critical behavior of systems with long-range correlated defects.: Phys. Rev., 2000, v. B62 №13.

2.Ландау Л.Д. Лифшиц Е.М. Статистическая физика. М.: Наука, 1976.

3.Доценко В.С. УФН, 1995, т.165, № 5.

4.Гулд Х., Тобочник Я.К. "Компьютерное моделирование в физике" В 2 ч.: Наука 1989

5.Kun Chen, Alan M. Ferrenberg, and D. P. Landau. Static critical behavior of three dimensional classical Heisenberg models: A high-resolution Monte Carlo study. Phys. Rev., 1993, v. B 48, p.3249-3256.

6.Grobe S. Pawing, Pinn K. Monte Carlo Algorithms For Fully Frustrated XY Model. arXiv: cond-mat/9807137.

7.Zheng B. Monte Carlo simulations and numerical solutions of short-time critical dynamics. arXiv: cond-mat/9910504.