Конспект урока по теме: "Движение тела по окружности с постоянной по модулю скоростью"

Автор: Александрова Зинаида Васильевна, учитель физики и информатики

Образовательное учреждение: МОУ СОШ №5 п.Печенга, Мурманская обл.

Движение тела по окружности с постоянной по модулю скоростью

Цель:

дать представление о криволинейном движении, ввести понятия частоты, периода, угловой скорости, центростремительного ускорения и центростремительной силы.
Развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету.
формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность.

Оснащение урока: компьютер, проектор, экран, презентация к уроку «Движение тела по окружности», распечатка карточек с заданиями.

Оборудование к демонстрациям: теннисный шара, волан для бадминтона, игрушечный автомобиля, шарика на нити, штатив.

Тип урока: урок изучения нового материала, комбинированный.

Ход урока

Организационный момент.

Слайд 1. (Проверка готовности к уроку, объявление темы и целей урока.)

Учитель. Сегодня на уроке вы узнаете, что такое ускорение при равномерном движении тела по окружности и как его определить.

Актуализация опорных знаний.

Слайд 2.

Физический диктант:

Изменение положения тела в пространстве с течением времени. (Движение)
Физическая величина, измеряемая в метрах. (Перемещение)
Физическая векторная величина, характеризующая быстроту движения. (Скорость)
Основная единица измерения длины в физике. (Метр)
Физическая величина, единицами измерения которой служат год, сутки, час. (Время)
Физическая векторная величина, которую можно измерить с помощью прибора акселерометра. (Ускорение)
Длина траектории. (Путь)
Единицы измерения ускорения (м/с²).

(Проведение диктанта с последующей проверкой, самооценка работ учениками)

Изучение нового материала.

Слайд 3.

Учитель. Мы достаточно часто наблюдаем такое движение тела, при котором его траекторией является окружность. По окружности движется, например, точка обода колеса при его вращении, точки вращающихся деталей станков, конец стрелки часов.

Демонстрации опытов 1. Падение теннисного шара, полёт волана для бадминтона, перемещение игрушечного автомобиля, колебания шарика на нити, закреплённого в штативе. Что общего и чем отличаются эти движения по виду? (Ответы учеников)

Учитель. Прямолинейное движение – это движение, траектория которого - прямая линия, криволинейное – кривая. Приведите примеры прямолинейного и криволинейного движения, с которыми вы встречались в жизни. (Ответы учеников)

Движение тела по окружности является частным случаем криволинейного движения.

Любую кривую можно представить как сумму дуг окружностей разного (или одинакового) радиуса.

Криволинейным движением называют такое движение, которое совершается по дугам окружностей.

Введём некоторые характеристики криволинейного движения.

Слайд 4. (просмотр видео «скорость.avi» по ссылке на слайде)

Криволинейное движение с постоянной по модулю скоростью. Движение с ускорением, т.к. скорость меняет направление.

Слайд 5. (просмотр видео «Зависимость центростремительного ускорения от радиуса и скорости. аvi» по ссылке на слайде)

Слайд 6. Направление векторов скорости и ускорения.

(работа с материалами слайда и анализ рисунков, рациональное использование эффектов анимации, заложенных в элементы рисунков, рис 1.)

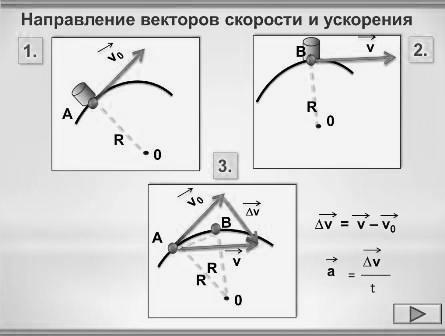
Рис.1.

Слайд 7.

При равномерном движении тела по окружности вектор ускорения всё время перпендикулярен вектору скорости, который направлен по касательной к окружности.

Тело движется по окружности при условии, что вектор линейной скорости перпендикулярен вектору центростремительного ускорения.

Слайд 8. (работа с иллюстрациями и материалами слайда)

Центростремительное ускорение - ускорение, с которым тело движется по окружности с постоянной по модулю скоростью, всегда направлено вдоль радиуса окружности к центру.

a_ц=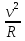

Слайд 9.

При движении по окружности тело через определённый промежуток времени вернётся в первоначальную точку. Движение по окружности – периодическое.

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.

Единица измерения периода - секунда

Частота вращения  – число полных оборотов в единицу времени.

[ ] = с^-1 = Гц

Единица измерения частоты

Сообщение ученика 1. Период - это величина, которая часто встречается в природе, науке и технике. Земля вращается вокруг своей оси, средний период этого вращения составляет 24 часа; полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток; винт вертолёта имеет средний период вращения от 0,15 до 0,3 с; период кровообращения у человека равен примерно 21 - 22 с.

Сообщение ученика 2. Частоту измеряют специальными приборами – тахометрами.

Частота вращения технических устройств: ротор газовой турбины вращается с частотой от 200 до 300 1/с; пуля, вылетевшая из автомата Калашникова, вращается с частотой 3000 1/с.

Слайд 10. Связь периода с частотой:

Если за время t тело совершило N полных оборотов, то период обращения равен:

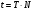
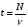
Период и частота – это взаимообратные величины: частота обратно пропорциональна периоду, а период обратно пропорционален частоте

Слайд 11. Быстроту обращения тела характеризуют угловой скоростью.

Угловая скорость (циклическая частота)- число оборотов за единицу времени, выраженное в радианах.

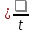
Угловая скорость – угол поворота, на который поворачивается точка за время t.

Угловая скорость измеряется в рад/с.

Слайд 12. (просмотр видео «Путь и перемещение при криволинейном движении.avi» по ссылке на слайде)

Слайд 13. Кинематика движения по окружности.

Учитель. При равномерном движении по окружности модуль его скорости не изменяется. Но скорость - векторная величина, и она характеризуется не только числовым значением, но и направлением. При равномерном движении по окружности всё время изменяется направление вектора скорости. Поэтому такое равномерное движение является ускоренным.

Линейная скорость: ;

Линейная и угловая скорости связаны соотношением:

Центростремительное ускорение: ;

Угловая скорость: ;

Слайд 14. (работа с иллюстрациями на слайде)

Направление вектора скорости. Линейная (мгновенная скорость) всегда направлена по касательной к траектории, проведенной к той ее точке, где в данный момент находится рассматриваемое физическое тело.

Вектор скорости направлен по касательной к описываемой окружности.

Равномерное движение тела по окружности является движением с ускорением. При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора.

Слайд 15. Центростремительная сила.

Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой.

Чтобы получить формулу для расчёта величины центростремительной силы, надо воспользоваться вторым законом Ньютона, который применим и к любому криволинейному движению.

Подставляя в формулу 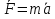значение центростремительного ускорения a_ц= 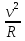, получим формулу центростремительной силы: F =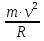

Из первой формулы видно, что при одной и той же скорости чем меньше радиус окружности, тем больше центростремительная сила. Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.

Центростремительная сила зависит от линейной скорости: с увеличением скорости она увеличивается. Это хорошо известно всем конькобежцам, лыжникам и велосипедистам: чем с большей скоростью движешься, тем труднее сделать поворот. Шофёры очень хорошо знают, как опасно круто поворачивать автомобиль на большой скорости.

Слайд 16.

Сводная таблица физических величин, характеризующих криволинейное движение (анализ зависимостей между величинами и формулами)

Слайды 17, 18, 19. Примеры движение по окружности.

Круговое движение на дорогах. Движение спутников вокруг Земли.

Слайд 20. Аттракционы, карусели.

Сообщение ученика 3. В Средние века каруселями (слово тогда имело мужской род) называли рыцарские турниры. Позднее, в XVIII веке, для подготовки к турнирам, вместо схваток с реальными соперниками, стали использовать вращающуюся платформу, прообраз современной развлекательной карусели, которая тогда же появилась на городских ярмарках.

В России первый карусель был построен 16 июня 1766 года перед Зимним дворцом. Карусель состоял из четырёх кадрилей: Славянской, Римской, Индийской, Турецкой. Второй раз карусель была построена на том же месте, в том же году 11 июля. Подробное описание этих каруселей приводятся в газете Санкт-Петербургские ведомости 1766 года.

Карусель, распространённая во дворах в советское время. Карусель может приводиться в движение как двигателем (обычно электрическим), так и силами самих крутящихся, которые перед тем как сесть на карусель, раскручивают её. Такие карусели, которые нужно раскручивать самим катающимся, часто устанавливают на детских игровых площадках.

Кроме аттракционов, каруселями часто называют другие механизмы, имеющие сходное поведение — например, в автоматизированных линиях по разливу напитков, упаковке сыпучих веществ или производству печатной продукции.

В переносном смысле каруселью называют череду быстро сменяющихся предметов или событий.

Закрепление нового материала.

Учитель. Сегодня на этом уроке мы познакомились с описанием криволинейного движения, с новыми понятиями и новыми физическими величинами.

Беседа по вопросам:

Что называется периодом и частотой? Как связаны между собой эти величины? В каких единицах измеряются? Как их можно определить?
Что называется угловой скоростью? В каких единицах она измеряется? Как можно её рассчитать?
Что называют угловой скоростью? Что является единицей угловой скорости?
Как связаны угловая и линейная скорости движения тела?
Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?

Слайд 21.

Задание 1. Заполните таблицу, решив задачи по исходным данным (Рис.2), затем мы сверим ответы. (Ученики работают самостоятельно с таблицей, необходимо заранее приготовить распечатку таблицы для каждого ученика)

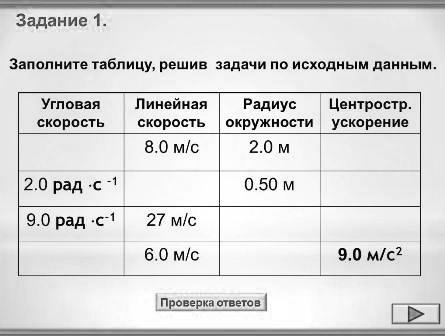
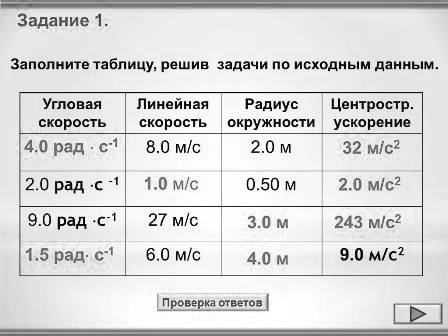
$C:\Users\Zinaida\Desktop\Рисунок1.jpg$ $C:\Users\Zinaida\Desktop\Рисунок2.jpg$

Рис.2

Слайд 22. Задание 2. (устно)

Обратите внимание на анимационные эффекты рисунка. Сравните характеристики равномерного движения синего и красного шара. (Работа с иллюстрацией на слайде)

Слайд 23. Задание 3. (устно)

Колёса представленных видов транспорта за одно и то же время совершают равное количество оборотов. Сравните их центростремительные ускорения. (Работа с материалами слайда)

Слайды 24 -29.

Фронтальная работа с интерактивным тестом.

Необходимо выбрать один ответ из трёх возможных, если был выбран правильный ответ, то он остаётся на слайде, и начинает мигать зелёный индикатор, неверные ответы исчезают.

Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 3 раза?
В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. Как при этом направлен вектор его ускорения?
Конькобежец движется со скоростью 10 м/с по окружности радиусом 20 м. Определите его центростремительное ускорение.
Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью?
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить втрое?
Колесо машины делает 20 оборотов за 10 с. Определите период обращения колеса?

Слайд 30. Решение задач (самостоятельная работа при наличии времени на уроке)

Вариант 1.

С каким периодом должна вращаться карусель радиусом 6,4 м для того, чтобы центростремительное ускорение человека на карусели было равно 10 м/с²?

На арене цирка лошадь скачет с такой скоростью, что за 1 минуту обегает 2 круга. Радиус арены равен 6,5 м. Определите период и частоту вращения, скорость и центростремительное ускорение.

Вариант 2.

Частота обращения карусели 0,05 с^-1. Человек, вращающийся на карусели, находится на расстоянии 4 м от оси вращения. Определите центростремительное ускорение человека, период обращения и угловую скорость карусели.

Точка обода колеса велосипеда совершает один оборот за 2 с. Радиус колеса 35 см. Чему равно центростремительное ускорение точки обода колеса?