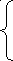
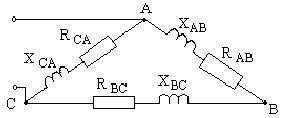
Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Череповецкий Государственный Университет

Кафедра Электропривода и электротехники

Курсовая работа

по дисциплине «Электротехника и электроника»

Выполнил студент

группы 5 ЭН – 22

Малинин М.С.

Проверил доцент

Кудрявцева А.К.

г. Череповец

2007 г

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

ОСНОВНАЯ ЧАСТЬ 6

ЗАДАЧА 1 6

Метод контурных токов 7

Метод узловых потенциалов 9

ЗАДАЧА 2 11

ЗАДАЧА 3 13

ЗАДАЧА 4 15

СПИСОК ЛИТЕРАТУРЫ 17

ВВЕДЕНИЕ

Полупроводниковый диод, двухэлектродный электронный прибор на основе полупроводникового (ПП) кристалла. Понятие «Полупроводниковый диод» объединяет различные приборы с разными принципами действия, имеющие разнообразное назначение.

В полупроводниковых диодах используется свойство p-n перехода, а также других электрических переходов, а также других электрических переходов хорошо проводить электрический ток в одном направлении и плохо – в противоположном. Эти токи и соответствующие им напряжения между выводами диода называются прямым и обратным токами, прямым и обратным напряжениями.

По способу изготовления различают сплавные диоды, диоды с диффузионной базой и точечные диоды. В диодах двух первых типов переход получается методами сплавления пластин p- и n-типов или диффузии в исходную полупроводниковую пластину примесных атомов. При этом p-n-переход создается на значительной площади (до 1000 мм²). В точечных диодах площадь перехода меньше 0,1 мм². они применяются главным образом в аппаратуре сверхвысоких частот при значении прямого тока 10 – 20 мА.

По функциональному назначению полупроводниковые диоды делятся на выпрямительные, импульсные, стабилитроны, фотодиоды, светоизлучающие диоды и т.д.

Выпрямительные диоды предназначены для преобразования переменного тока и выполняются по сплавной или диффузионной технологии. Прямой ток диода направлен от анодного А к катодному К выводу. Нагрузочную способность выпрямительного диода определяют: допустимый прямой ток I_пр и соответствующее ему прямое напряжение U_пр, допустимое обратное напряжение U_обр и соответствующий ему обратный ток I_обр, допустимая мощность рассеяния P_рас и допустимая температура окружающей среды (до 50 ⁰С для германиевых и до 140 ⁰С для кремниевых диодов).

Вследствие большой площади p-n-перехода допустимая мощность рассеяния выпрямительных диодов малой мощности с естественным охлаждением достигает 1 Вт при значениях прямого тока до 1 А. Такие диоды часто применяются в цепях автоматики и в приборостроении. У выпрямительных диодов большой мощности с радиаторами и искусственным охлаждением (воздушным или водяным) допустимая мощность рассеяния достигает 10 кВт при значениях допустимых прямого тока до 1000 А и обратного напряжения до 1500 В.

Импульсные диоды предназначены для работы в цепях формирования импульсов напряжения и тока.

Стабилитроны, называемые также опорными диодами, предназначены для стабилизации напряжения. В этих диодах используется явление неразрушающего электрического пробоя (лавинного пробоя) p-n-перехода при определенных значениях обратного напряжения U_обр = U_проб.

Следует отметить основные причины отличия характеристик реальных диодов от идеализированных. Обратимся к прямой ветви вольт-амперной характеристики диода (u > 0, ί > 0). Она отличается от идеализированной из-за того, что в реальном случае на нее влияют:

• сопротивления слоев полупроводника (особенно базы);

• сопротивления контактов металл-полупроводник.

Важно, что сопротивление базы может существенно зависеть от уровня инжекции (уровень инжекции показывает, как соотносится концентрация инжектированных неосновных носителей в базе на границе перехода с концентрацией основных носителей в базе). Влияние указанных сопротивлений приводит к тому, что напряжение на реальном диоде при заданном токе несколько больше (обычно на доли вольта).

Обратимся к обратной ветви (u < 0, ί < 0). Основные причины того, что реально обратный ток обычно на несколько порядков больше теплового тока ί_s, следующие:

• термогенерация носителей непосредственно в области p-n-перехода;

• поверхностные утечки.

Термогенерация в области p-n-перехода оказывает существенное влияние на ток потому, что область перехода обеднена подвижными носителями заряда, и процесс рекомбинации (обратный процессу генерации и в определенном смысле уравновешивающий его) здесь замедлен.

ОСНОВНАЯ ЧАСТЬ

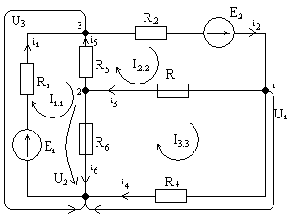
ЗАДАЧА 1 Линейные электрические цепи постоянного тока

Для электрической схемы выполнить следующее:

• Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными, а источники тока преобразовать в источники напряжения. Дальнейший расчет вести для упрощенной схемы.

• Указать на схеме положительное направление токов в ветвях и обозначить эти токи.

• Определить токи во всех ветвях схемы методом контурных токов.

• Определить токи во всех ветвях схемы методом узловых потенциалов.

Метод контурных токов

Дано:

R₁ = 19,5 Ом E₁ = 25,8 В

R₂ = 60 Ом E₂ = 37,5 В

R₃ = 90 Ом E₃ = 0 В

R_4.1 = 150 Ом I₁ = 0,04 А

R_4.2 = 600 Ом I₂ = 0 А

R₅ = 165 Ом I₃ = 0 А

R_6.1 = 40 Ом R_6.2 = 27,5 Ом

Решение:

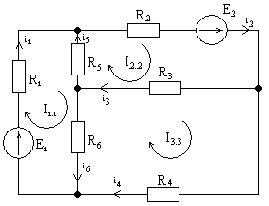
1. Находим в схеме элементы, соединенные параллельно или последовательно, и заменяем их эквивалентными

R₄ = R_4.1· R_4.2 / (R_4.1 + R_4.2 ) = 150 · 600 / (150 + 600) = 120 Ом

R₆ = R_6.1 + R_6.2 = 40 + 27,5 = 67,5 Ом

2. Определяем ЭДС

E₁^’ = I₁ · R₁ = 0,04 · 19,5 = 0,78 В

E₂^’ = I₂ · R₂ = 0 · 60 = 0 В

E₁^* = E₁ – E₁^’ = 25,8 – 0,78 = 25,02 В

E₂^* = E₂^’ – E₂ = 37,5 – 0 = 37,5 В

3. Составляем систему уравнений

I_1.1 · (R₁ + R₅ + R₆) – I_2.2 · R₅ – I_3.3 · R₆ = E₁

I_1.1 · R₅ + I_2.2 · (R₂ + R₃ + R₅) – I_3.3 · R₃ = – E₂

₆ – I_2.2 · R₃ + I_3.3 · (R₃ + R₄ + R₆) = 0

Переписываем систему уравнений с числовыми коэффициентами

I_1.1 · (19,5 + 165 + 67,5) – I_2.2 · 165 – I_3.3 · 67,5 = 25,02

– I_1.1 · 165 + I_2.2 · (60 + 90 + 165) – I_3.3 · 90 = 37,5

I_1.1 · 67,5 – I_2.2 · 90 + I_3.3 · (90 + 120 + 67,5) = 0

252 I_1.1 – 165 I_2.2 – 67,5 I_3.3 = 25,02

– 165 I_1.1 + 315 I_2.2 – 90 I_3.3 = 37,5

– 67,5 I_1.1 – 90 I_2.2 + 277,5 I_3.3 = 0

4. Считаем определители системы

252 – 165 – 67,5

Δ = – 165 315 – 90 = 22 027 950 – 1 002 375 – 1 002 375 –

– 67,5 – 90 277,5

– 1 435 218,75 – 2 041 200 – 7 554 937,5 = 8 991 843,75

25,02 – 165 – 67,5

Δ₁ = 37,5 315 – 90 = 2 187 060,75 + 2 278 812,5 +

0 – 90 277,5

+ 797 343,75 – 202 662 + 1 717 031,25 = 4 726 586,25

252 25,02 – 67,5

Δ₂ = – 165 37,5 – 90 = 2 622 375 + 151 996,5 –

– 67,5 0 277,5

• 170 859,375 + 1 145 603,25 = 3 749 115,375

252 – 165 25,02

Δ₃ = – 165 315 37,5 = 371 547 + 417 656,25 + 531 987,75 +

– 67,5 – 90 0

+ 850 500 = 2 171 691

5. Определяем контурные токи

I_1.1 = Δ₁ / Δ = 0,526

I_2.2 = Δ₂ / Δ = 0,417

I_3.3 = Δ₃ / Δ = 0,242

6. Используя II закон Кирхгофа, определяем токи в цепях

ί₁ = I_1.1 = 0,526 А ί₄ = I_3.3 = 0,242 А

ί₂ = I_2.2 = 0,417 А ί₅ = I_2.2 – I_1.1 = – 0,109 А

ί₃ = I_2.2 – I_3.3 = 0,175 А ί₆ = I_1.1 – I_3.3 = 0,284 А

7. Проверка

ί₅ + ί₁ – ί₂ = – 0,109 + 0,526 – 0,417 = 0

ί₃ – ί₆ – ί₅ = 0,175 – 0,284 + 0,109 = 0

ί₆ + ί₄ – ί₁ = 0,284 + 0,242 – 0,526 = 0

ί₂ – ί₃ – ί₄ = 0,417 – 0,175 – 0,242 = 0

Метод узловых потенциалов

Дано:

R₁ = 19,5 Ом E₁ = 25,8 В

R₂ = 60 Ом E₂ = 37,5 В

R₃ = 90 Ом E₃ = 0 В

R_4.1 = 150 Ом I₁ = 0,04 А

R_4.2 = 600 Ом I₂ = 0 А

R₅ = 165 Ом I₃ = 0 А

R_6.1 = 40 Ом R_6.2 = 27,5 Ом

Решение:

1. Определяем собственную проводимость узла, которая равна сумме проводимостей, сходящихся в узле

g₁ = 1 / R₁ = 0,05 g₄ = 1 / R₄ = 0,01

g₂ = 1 / R₂ = 0,02 g₅ = 1 / R₅ = 0,01

g₃ = 1 / R₃ = 0,01 g₆ = 1 / R₆ = 0,01

2. Определяем взаимную проводимость в узле, которая равна проводимости ветви, соединяющей два узла

g_1.1 = g₄ + g₂ + g₃ = 0,04 g_1.2 = g_2.1 = g₃ = 0,01

g_2.2 = g₃ + g₅ + g₆ = 0,03 g_2.3 = g_3.2 = g₅ = 0,01

g_3.3 = g₁ + g₂ + g₅ = 0,08 g_1.3 = g_3.1 = g₂ = 0,02

3. Определяем сумму токов от источников, которые находятся в ветвях, сходящихся в данном узле

I_1.1 = – E₂ / R₂ = – 37,5 / 60 = – 0,625

I_2.2 = 0

I_3.3 = E₁ / R₁ + E₂ / R₂ = 25,02 / 19,5 + 37,5 / 60 = 1,905

4. Записываем в общем виде систему уравнений

u₁ · g_1.1 – u₂ · g_1.2 – u₃ · g_1.3 = I_1.1

– u₁ · g_2.1 + u₂ · g_2.2 – u₃ · g_2.3 = I_2.2

– u₁ · g_3.1 – u₂ · g_3.2 + u₃ · g_3.3 = I_3.3

5. Переписываем систему уравнений с числовыми коэффициентами

0,04 u₁ – 0,01 u₂ – 0,02 u₃ = – 0,63

– 0,01 u₁ + 0,03 u₂ – 0,01 u₃ = 0

– 0,02 u₁ – 0,01 u₂ + 0,08 u₃ = 1,91

6. Считаем определители системы

0,04 – 0,01 – 0,02

Δ = – 0,01 0,03 – 0,01 = 0,000096 – 0,000002 – 0,000002 –

– 0,02 – 0,01 0,08

– 0,000012 – 0,000004 – 0,000008 = 0,000068

– 0,63 – 0,01 – 0,02

Δ₁ = 0 0,03 – 0,01 = – 0,001512 + 0,000191 + 0,001146 +

1,91 – 0,01 0,08

+ 0,000063 = – 0,000112

0,04 – 0,63 – 0,02

Δ₂ = – 0,01 0 – 0,01 = – 0,000126 + 0,000382 + 0,000764 –

– 0,02 1,91 0,08

– 0,000504 = 0,000516

0,04 – 0,01 – 0,63

Δ₃ = 0,01 0,03 0 = 0,002292 – 0,000063 – 0,000378 –

– 0,02 – 0,01 1,91

– 0,000191 = 0,00166

7. Определяем узловые напряжения

U_1.1 = Δ₁ / Δ = – 1,647 В

U_2.2 = Δ₂ / Δ = 7,588 В

U_3.3 = Δ₃ / Δ = 24,412 В

8. Используя II закон Кирхгофа, определяем токи в ветвях

ί₁ = (E₁ – U₃) / R₁ = (25,02 – 24,412) / 19,5 = 0,03 А

ί₂ = (– E₂ – U₁ + U₃) / R₂ = (– 37,5 + 1,647 + 24,412) / 60 = – 0,19 А

ί₃ = (U₁ – U₂) / R₃ = (– 1,647 – 7,588) / 90 = – 0,1 А

ί₄ = U₁ / R₄ = – 1,647 / 120 = – 0,01 А

ί₅ = (– U₃ + U₂) / R₅ = (– 24,412 + 7,588) / 165 = – 0,1 А

ί₆ = U₂ / R₆ = 7,588 / 67,5 = 0,11 А

9. Проверка

ί₅ + ί₁ – ί₂ = – 0,1 + 0,03 + 0,191 = 0,12

ί₃ – ί₆ – ί₅ = – 0,1 – 0,11 + 0,11 = – 0,11

ί₆ + ί₄ – ί₁ = 0,11 – 0,01 – 0,03 = 0,07

ί2 – ί3 – ί4 = – 0,19 + 0,1 + 0,01 = – 0,08

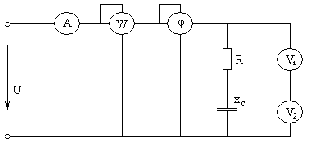
ЗАДАЧА 2 Линейные электрические цепи синусоидального тока

В сеть переменного тока с действующим значением напряжения U включена цепь, состоящая из двух параллельных ветвей. Определить показания приборов, реактивную мощность цепи, коэффициент мощности и построить векторную диаграмму напряжений. Указать на схеме положительное направление токов в ветвях и обозначить эти токи.

Дано:

R₁ = 8 Ом

R₂ = 2 Ом

U = 127 В

јx _c = 17 Ом

Решение:

1. Примем начальную фазу напряжения равной нулю

Ů = 127 е ^ј0 В

2. Определяем комплексное сопротивление

z ₁ = R₁ = 8 Ом

z ₂ = R₂ – јx _c = √2 ² + 17 ² · е ^{– ј arctg 17/4} = 17,1 е ^{– 77}

3. По закону Ома определяем комплексные точки

İ ₁ = Ů / z ₁ = 127 е ^ј0 / 8 = 15,9 е ^ј0 А

İ ₂ = Ů / z ₂ = 127 е ^ј0 / 17,1 е ^{– 77} = 7,4 е ^{ј 77} =

= 7,4 · cos 77 + ј 7,4 · sin 77 = 1,7 + ј 7,2

4. Определяем полный комплексный ток

İ = İ ₁ + İ ₂ = 15,9 е ^ј0 + 7,4 е ^{ј 77} = 15,9 cos 0 + ј 15,9 sin 0 +

+ 7,4 cos 77 + ј 7,4 sin 77 = 17,5 + ј 7,2 =

= √17,5 ² + 7,2 ² · е ^{ј arctg 7,23/17,544} = 18,9 · е ^{ј 22}

А 18,9 А

А₁ 15,9 А

А₂ 7,4 А

5. Определяем полную мощность

S = İ · Ů = 18,9 е ^{ј 22} · 127 е ^ј0 = 2410,5 е ^{ј 22} =

= 2410,5 cos 22 + ј 2410,5 sin 22 = 2234,9 + ј 902,9

İ = 18,9 · е ^{ј 22} S = 2410,5 ВА

P = 2234,9 Вт Q = 902,9 ВАР

6. Определяем коэффициент мощности

cos φ = P / S = 0,93

ЗАДАЧА 3 Линейные электрические цепи синусоидального тока

В цепь переменного тока с мгновенным значением напряжения

U = U _m sin ωt промышленной частоты f = 50 Гц включены резистор и конденсатор. Определить показания приборов, реактивную и полную мощность цепи. Построить треугольник напряжений и векторную диаграмму напряжений.

Дано:

R = 2 Ом

U_m = 282 В

x _c = 17 Ом

Решение:

1. Определяем напряжение на зажимах цепи

U = U_m / √2 = 282 / 1,41 = 200 В

2. Определяем накопленное емкостное сопротивление

– јx _c = – ј 17 = 17 е ^{– ј 90}

3. Определяем полное комплексное сопротивление цепи z

Z = R – јx _c = 2 – ј 17 = √2 ² + 17 ² · е ^{– ј arctg 17/2} = 17,1 е ^– ј ⁸³

4. Начальную фазу напряжения примем равной нулю

Ů = 200 е ^ј0 В

5. Определяем комплексный ток по закону Ома

İ = Ů / Z = 200 е ^ј0 / 17,1 е ^– ј ⁸³ = 11,7 е ј ⁸³

тогда показания амперметра I_А = 11,7 А

6. Определяем комплексное напряжение на R

Ů_R = I R = 11,7 е ј ⁸³ · 2 = 23,4 е ј ⁸³ =

= 23,4 cos 83 + ј 23,4 sin 83= 2,9 + ј23,2

7. Определяем напряжение на емкости

Ů_c = İ (^– ј x _c) = 11,7 е ј ⁸³ · 17 е ^{– ј 90} = 198,6 е ^{– ј 7} =

= 198,6 cos 7 ^– ј 198,6 sin 7 = 197,1 ^– ј 24,2

тогда показания вольтметра U_c = 198,6 В

8. Определяем полную комплексную мощность цепи

Ŝ = I* · Ů = 11,7 е ^-ј ⁸³ · 200 е ^ј0 = 2336 е ^{-ј 83} =

= 2336 cos 83 – ј 2336 sin 83 = 284,7 – ј 2318,6

S = 2336 ВА

P = 284,7Вт Q = 2318,6 ВАР

9. Определяем показатель фазометра

φ = φ_u – φ_ί = 0 – 83 = – 83

тогда показания фазометра cos φ = cos (– 83) = 0,12

ЗАДАЧА 4 Трехфазные электрические цепи синусоидального тока

В трехфазную сеть с линейным напряжением U_л (действующее значение напряжения) по схеме «треугольник/треугольник» включены активно-индуктивные приемники. Определить фазные и линейные токи в нагрузке, активную мощность всей цепи и каждой фазы отдельно.

Дано:

R_АВ = 8 Ом U_л = 127 В X_СА = 3 Ом R_СА = 2 Ом

R_ВС = 3 Ом X_АВ = 6 Ом X_ВC = 17 Ом

Решение:

1. Т. к. рассматриваем соединение «треугольник/треугольник», то

U_п = U_до

Ů_АВ = 127 е ^{ј 0}

Ů_ВС = 127 е ^{– ј 120}

Ů_СА = 127 е ^{ј 120}

2. Определяем комплексное полное сопротивление фаз

z_АВ = R_АВ + ј x_АВ = 8 + ј 6 = √8² + 6² · е ^{ј arctg 6/8} = 10 е ^ј37

z_ВC = R_ВC + ј x_ВC = 3 + ј 17 = √3² + 17² · е ^{ј arctg 17/3} = 17,3 е ^ј80

z_CА = R_СА + ј x_СА = 2 + ј 3 = √2² + 3² · е ^{ј arctg 3/2} = 3,6 е ^ј56

3. Определяем комплексные фазные токи

I_ф = U_ф / z_ф

İ_АВ = 127 е ^{ј 0} / 10 е ^ј37 = 12,7 е ^-ј37

İ_ВС = 127 е ^{-ј 120} / 17,3 е ^ј80 = 7,3 е ^-ј200

İ_СА = 127 е ^{ј 120} / 3,6 е ^ј56 = 35,3 е ^ј64

4. Определим сопряженные комплексные токи фаз:

İ_АВ^* = 12,7 е ^ј37

İ_ВС^* = 7,3 е ^ј200

İ_СА^* = 35,3 е ^-ј64

5. Определяем комплексные полные мощности фаз

S = I_Ф^* · U_Ф

S_АВ = 12,7 е ^ј37 · 127 е ^{ј 0} = 1612,9 е ^ј37 = 1612,9 cos 37 + ј 1612,9 sin 37 = 1288,1 + ј 970,7

S_ВC = 7,3 е ^ј200 · 127 е ^{– ј 120} = 927,1 е ^-ј80 =

= 927,1 cos 80 – ј 927,1 sin 80 = 161 – ј 913

S_CА = 35,3 е ^-ј64 · 127 е ^{ј 120} = 4483,1 е ^ј56 = 4483,1 cos 56 + ј 4483,1 sin 56 =

= 2506,9 + ј 3716,7

6. Определяем активную мощность фаз

P_АВ = 1288,1 Вт

P_ВC = 161 Вт

P_CА = 2506,9 Вт

7. Определяем активную мощность цепи

P_ц = P_АВ + P_ВC + P_CА = 3956 Вт

СПИСОК ЛИТЕРАТУРЫ

1. Касаткин А. С., М. В. Немцов «Электротехника»: М., Академия, 2005.

2. Методические указания к выполнению контрольной работы по дисциплине «Общая электротехника и электроника» для студентов заочной формы обучения.

3. Лачин В.И., Н.С. Савёлов «Электроника»: М., Феникс, 2002.

4. Лекции по дисциплине «Общая электротехника и электроника».