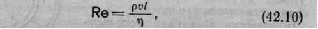
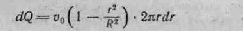
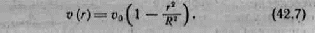
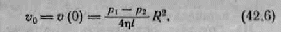
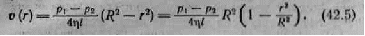
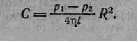
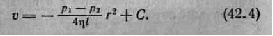
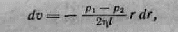
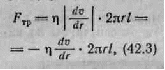
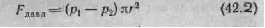
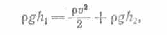
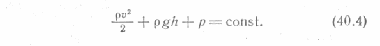
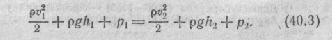
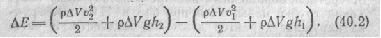
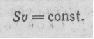
ГОУ ВПО

ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

Реферат на тему:

МЕХАНИКА ЖИДКОСТЕЙ и газов

Выполнил:

Студент гр. МС-116

Оконешников А.В.

Проверил:

Шевченко С.С.

Омск - 2007

1. МЕХАНИКА ЖИДКОСТЕЙ

Совокупность векторов v(t), заданных для всех точек пространства, называется полем вектора скорости. Это поле можно наглядно изобразить с помощью линий тока (рис. 39.1). Линию тока

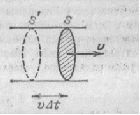
Рис.39.2. За время Δt через поверхность S пройдут все частицы жидкости, заключённые в объёме между S и S’

Рис. 39.1. Линии тока проводятся так, чтобы вектор v в каждой точке пространства был направлен по касательной к соответствующей линии

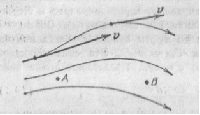
можно провести через любую точку пространства. Если построить все мыслимые линии тока, они просто сольются друг с другом. Поэтому для наглядного представления течения жидкости строят лишь часть линий, выбирая их так, чтобы густота линий тока была численно равна модулю скорости в данном месте. Тогда по картине линий тока можно судить не только о направлении, но и о модуле вектора v в разных точках пространства. Например, в точке А на рис.39.1 густота линий, а следовательно и модуль v, чем в точке В. Поскольку разные частицы жидкости могут проходить через данную точку пространства с разными скоростями (т. е. v = v(t)), картина линий тока, вообще говоря, все время изменяется. Если скорость в каждой точке пространства остается постоянной (V=const), то течение жидкости Называется стационарным (установившимся). При стационарном течении любая частица жидкости проходит через данную точку пространства с одной и той же скоростью v. Картина линий тока при стационарном течении остается неизменной, и линии тока в этом случае совпадают с траекториями частиц. Если через все точки небольшого замкнутого контуpa провести линии тока, образуется поверхность, которую называют трубкой тока. Вектор v касателен к поверхности трубки тока в каждой ее точке. Следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока.

Возьмем трубку тока, достаточно тонкую для того, чтобы во всех точках ее поперечного сечения S скорость частиц v была одна и та же (рис. 39.2). При стационарном течении трубка тока подобна стенкам жесткой трубы. Поэтому через сечение 5 пройдет за время Δt объем жидкости, равный SvΔt, а в единицу времени объем

(39.1)

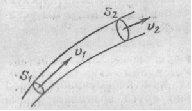
Жидкость, плотность которой всюду одинакова и изменяться не может, называется несжимаемой. На рис. 39.3 изображены два сечения очень тонкой трубки тока — S1 и S2. Если жидкость несжимаема , то кол – во ее между этими сечениями остается неизменным. Отсюда следует, что

Рис39.3. Для несжимаемой жидкости при стационарном течении S₁v₁=S₂v₂

Рис 39.4. При движении в сужающейся трубке скорость частиц возрастает – частицы движутся ускоренно.

объемы жидкости, протекающие в единицу времени через сечения S1 и S2, должны быть одинаковыми:

(39.2)

(напомним, что через боковую поверхность трубки тока частицы жидкости не проникают).

Равенство (39.2) справедливо для любой пары произвольно взятых сечений. Следовательно, для несжимаемой жидкости при стационарном течении произведение Sv в любом сечении данной трубки тока имеет одинаковое значение:

(39.3)

Это утверждение носит название теоремы о неразрывности струи.

Мы получили формулу (39.3) для несжимаемой жидкости. Однако она применима к реальным жидкостям и даже к газам в том случае, когда их сжимаемостью можно пренебречь. Расчеты показывают, что при движении газов со скоростями, много меньшими скорости звука в этой среде, их можно с достаточной точностью считать несжимаемыми.

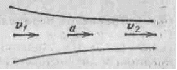
Из соотношения (39.3) вытекает, что при изменяющемся сечении трубки тока частицы несжимаемой жидкости движутся с ускорением (рис. 39.4). Если трубка тока горизонтальна, это ускорение может быть обусловлено только непостоянством давления вдоль трубки — в местах, где скорость больше, давление должно быть меньше, и наоборот. Аналитическую связь между скоростью течения и давлением мы установим в следующем параграфе.

2. Уравнение Бернулли

В реальных жидкостях при перемещении слоев жидкости друг относительно друга возникают силы внутреннего трения, тормозящие относительное смещение слоев. Воображаемая жидкость, у которой внутреннее трение полностью отсутствует, называется идеальной. Течение идеальной жидкости не сопровождается диссипацией энергии (см. предпоследний абзац § 24).

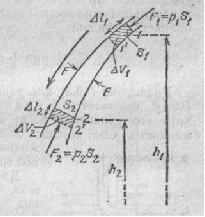
Рассмотрим стационарное течение несжимаемой идеальной жидкости. Выделим объем жидкости, ограниченный стенками узкой трубки тока и перпендикулярными к линиям тока сечениями S₁ и S₂ (рис. 40.1), За время А/ этот объем сместится вдоль трубки тока, причем граница объема S₁ получит перемещение Δl₂ , а граница S₂ — перемещение Δl₂. Работа, совершаемая при этом силами давления, раина приращению полной энергии (E_k + E_p)_, заключенной в рассматриваемом объеме жидкости.

Силы давления на стенки трубки тока перпендикулярны в каждой точке к направлению перемещения жидкости, вследствие чего работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям S1 и S2. Эта работа равна (см. рис. 40.1).

Полная энергия рассматриваемого объема жидкости слагается из кинетической энергии и потенциалальной энергии в поле сил земного тяготения. Вследствие стационарности течения полная энергия той части жидкости, которая ограничена сечениями 1’ и 2 (внутренняя незаштрихованная часть трубки тока на рис. 40.1), за время Δt не изменяется. Поэтому приращение полной энергии равно разности значений полной энергии заштрихованных объемов ΔV₂ и ΔV₁, масса которых Δm = рΔV (р — плотность жидкости).

Возьмем сечение S трубки тока и перемещения Δl настолько малыми, чтобы всем точкам каждого из заштрихованных объёмов можно было приписать одно и то же значение скорости v , давления p, и высоты h. Тогда дли приращения полной энергии получается выражение

Приравняв выражения (40.1) и (40.2), сократив на AV и перенеся члены с одинаковыми индексами в' одну часть равенства, придем к уравнению

Это уравнение становится вполне строгим лишь при стремлении поперечного сечения S к нулю, т. е. при стягивании трубки тока в линию. Следовательно, величины и, h и р в обеих частях равенства нужно рассматривать как относящиеся к двум произвольным точкам одной и той же линии тока.

При выводе формулы (40.3) сечения S₁ и S₂ были взяты совершенно произвольно. Поэтому можно утверждать, что в стационарно текущей несжимаемой и идеальной жидкости вдоль любой линии тока выполняется условие

Уравнение (40.3) или равнозначное ему уравнение (40.4) называется уравнением Бернулли. Хотя это уравнение было получено для идеальной жидкости, оно хорошо выполняется для реальных жидкостей, у которых внутреннее трение невелико.

3. Истечение жидкости из отверстия

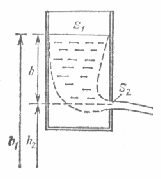
Рассмотрим истечение идеальной несжимаемой жидкости из небольшого отверстия в широком открытом сосуде (рис. 41.1). Выделим мысленно в жидкости трубку тока, сечениями которой являются открытая поверхность жидкости S₁ и сечение струи при выходе из отверстия S₂ (если не принять специальных мер, то сечение струи будет меньше отверстия). Для всех точек каждого из этих сечений скорость жидкости v и высоту h над некоторым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления р₁ и р₂ в обоих сечениях одинаковы и равны атмосферному. Скоростью v₁ перемещения открытой поверхности жидкости ввиду ее малости можно пренебречь. Поэтому уравнение (40.3) в данном случае упрощается следующим образом:

Рис.41.1.

где v — скорость жидкости в сечении S₂ (скорость истечения из отверстия). Сократив на р, можно написать, что где h = h₁ — h₂ — высота открытой поверхности над отверстием.

Формула (41.1) называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине h под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты h (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.

4. Вязкость. Течение жидкости в трубах

Идеальная жидкость, т. е. жидкость без внутреннего трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуще внутреннее трение, называемое также вязкостью. Вязкость проявляется, в частности, в том, что возникшее в жидкости или газе движение, после прекращения действия причин, его вызвавших, постепенно прекращается. Примером может служить движение жидкости в стакане после того, как ее перестают размешивать ложечкой.

Рассмотрим течение жидкости в круглой трубе. Измерения показывают, что при медленном течении скорость частиц жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимума на оси трубы.

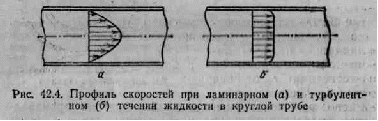
Жидкость при этом оказывается как бы разделенной на тонкие цилиндрические слои, которые скользят друг относительно друга, не перемешиваясь (рис. 42.1). Такое течение называется ламинарным или слоистым (латинское слово lamina означает пластинку, полоску). Отсутствие перемешивания слоев можно наблюдать, создав в стеклянной трубке диаметра несколько сантиметров слабый поток воды и вводя на оси трубы через узкую трубочку окрашенную жидкость (например, анилин). Тогда по всей длине трубы возникнет тонкая окрашенная струйка, имеющая отчетливую границу с водой.

Из повседневного опыта известно, что для того, чтобы Создать и поддерживать постоянным течение жидкости в трубе, необходимо наличие между концами трубы разности давлений. Поскольку при установившемся течении жидкость движется без ускорения, необходимость действия сил давления указывает на то, что эти силы, уравновешиваются какими-то силами, тормозящим движение. Этими силами является силы внутреннего трения на границе со стенкой трубы и на границах между слоями. Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой F₁ направленной по течению. Одновременно более медленный слой стрёмится замедлить движение более быстрого слон, действуя на него с силой F_2y направленном против течения (рис. 42.2).

Экспериментально установлено, что модуль СИЛЫ внутреннего трения, приложенной к площадке 5, лежащей на границе между слоями, определяется формулой

где n— называемый вязкостью коэффициент пропорциональности, зависящим от природы и состояния

(например, температуры) жидкости, dv/dz—производная, показывающая, как быстро изменяется в данном месте скорость течения в направлений г, перпендикулярном к площадке S. В случае качения жидкости в трубе ось z направлена в каждой точке границы между слоями по радиус} грубы (см. pиc, 42.1), Поэтому вместо dv/dz можно написать, dv/df, Знак модуля в формуле (42.1) поставлен в связи с тем, что в зависимости от выбора направления оси z и характера изменения скорости производная dv/dz может быть как положительной, так и отрицательной, в то время как модуль силы является положительной величиной.

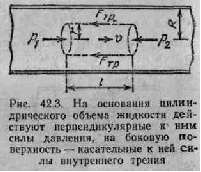
Мы уже отмечали, что при ламинарном течении жидкости в круглой трубе скорость равна нулю у стенки трубы и максимальна па оси трубы. Найдем закон изменения скорости. Выделим воображаемый цилиндрический объем жидкости радиуса r и длины l (рис. 42.3). При стационарном течении этот объем движется без ускорения. Следовательно, сумма приложенных к нему сил равна нулю. В направлении

движения на жидкость действует сила давления, модуль которой равен p₁Пr²; во встречном направлении— сила давления, модуль которой равен p₂Пr². Результирующая сил давления имеет модуль

(Пr² — площадь основания цилиндра).

На боковую поверхность действует тормозящая движение сила внутреннего трения, модуль которой

согласно формуле

(42.1) равен

где 2Пrl — площадь боковой поверхности цилиндра, dv/dr — значение производной на расстоянии r от оси трубы. Скорость убывает с расстоянием от оси труби, поэтому производная dv/dr отрицательна и ее модуль равен —dv/dr {модуль отрицательного числа равен этому числу, взятому с обратным знаком).

Приравняв выражения (42.2) и (42.3), придем к дифференциальному уравнению

Разделив переменные, получим уравнение

интегрирование которого дает, что

Постоянную интегрирования С нужно выбрать так, чтобы на стенке трубы (т. е. при г = R) скорость об* ращалась в нуль. Это условие выполняется при

Подстановка этого значения в (42.4) приводит к формуле

Скорость на оси трубы равна

С учетом этого формулу (42.5) можно написать в виде

Отсюда следует, что при ламинарном течения скорость изменяется с расстоянием от оси трубы но параболическому закону (рис. 42.4а).

С помощью формулы (42.7) можно вычисти, поток жидкости Q, т. е. объем жидкости, протекающей через поперечное сечение трубы и единицу времени. Разобьем сечение трубы на кольца ширины dr (рис. 42.5). Через кольцо радиуса r пройдёт в единицу времени объем жидкости dQ, равный произведению площади кольца 2Пrdr на скорость v(t) на расстоянии от оси трубы:

(мы воспользовались формулой (42.7)). Проинтегрировав это выражение по г в пределах ОТ пули до R, получим поток Q:

(S—площадь сечения трубы). Поток можно представить как произведение среднего по сечению значения скорости <и> на площадь 5. Из формулы (42.8) следует, что при ламинарном течении среднее значение скорости равно половине значения скорости на оси трубы.

Подставив в (42.8) выражение (42.6) дли с>о, получим формулу

которая называется ф о р м у л о й П у а з е й л я . Из нее следует, что поток очень сильно зависит от радиуса трубы.

Естественно, что Q пропорционален отношению {P₁ — Р₂) / l т. е. перепаду давления на единице длины трубы, а также обратно пропорционален вязкости жидкости n.

Формула Пуазейля используется для определения вязкости жидкостей и газов. Пропуская жидкость или газ через трубку известного радиуса, измеряют перепад давления и поток Q. Затем на основании полученных данных вычисляют n.

Мы все время подчеркивали, что предполагаем течение медленным для того, чтобы оно имело ламинарный характер. Напомним, что ламинарное течение является стационарным. Это означает, что скорость частиц жидкости, проходящих через данную точку пространства, все время одна и та же. Если увеличивать скорость течения, то при достижении определенного значения скорости характер течения резко меняется. Течение становится нестационарным — скорость частиц в каждой точке пространства все время беспорядочно изменяется. Такое течение называется турбулентным. При турбулентном течении происходит интенсивное перемешивание жидкости. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределится по всему сечению потока. Это можно наблюдать в упоминавшемся выше опыте, если увеличить поток воды в стеклянной трубке.

Поскольку при турбулентном течении скорость в каждой точке все время меняется, можно говорить только о среднем по времени значении скорости, которая при неизменных условиях течения оказывается постоянной в каждой точке пространства. Профиль средних скоростей для одного из сечений трубы при турбулентном течении показан на рис. 42.56. Сравнение с рис. 42.5 а показывает, что вблизи стенки трубы скорость изменяется гораздо сильнее, чем при ламинарном течении; в остальной части сечения скорость изменяется меньше.

Рейнольдс установил, что характер течения определяется значением безразмерной величины

где р— плотность жидкости (или газа), v — средняя по сечению трубы скорость потока, n - вязкость жидкости, l — характерный для поперечного сечения потока размер, например сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении. Величина Re называется числом Рейнольдса.

При малых значениях Re течение носит ламинарный характер. Начиная с некоторого значения Re, называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера трубы взять ее радиус (в этом случае Re = pvr/n), то критическое значение числа Рейнольдса оказывается равным примерно 1000 (если в качестве / взять диаметр трубы, то критическое значение Re будет равно 2000).

Число Рейнольдса служит критерием подобия для течения жидкостей в трубах, каналах и т. д. Например, характер течения различных жидкостей (или газов) в круглых трубах разных диаметров будет одинаковым, если каждому течению соответствует одно и то же значение Re.

В число Рейнольдса входит отношение плотности р и вязкости т). Величина

называется кинематической вязкостью. Чтобы отличить ее от v, величину n называют динамической вязкостью. Будучи выраженным через кинематическую вязкость, число Рейнольдса имеет вид

5. Движение тел в жидкостях и газах.

Воздействие жидкой или газообразной среды на движущееся в ней с постоянной скоростью v тело будет таким же, каким было бы действие на неподвижное тело набегающего на пего со скоростью v однородного потока жидкости или газа (в дальнейшем для краткости мы будем говорить только о жидкости, подразумевая при этом и газы). Следовательно, при выяснении сил, действующих на тело, безразлично, что считать движущимся — тело или среду. Удобно предполагать тело неподвижным, а среду движущейся. Поэтому мы будем, как правило, рассматривать действие на неподвижное тело набегающего

па пего потока, помня, что результаты, полученные в этом случае, будут справедливыми и для случая движения тела относительно неподвижной среды.

Силу F, с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скорости v невозмущенного потока силу X, называемую лобовым сопротивлением, и перпендикулярную к v силу У, называемую подъемной силой. Лобовое сопротивление слагается из сил давления и сил внутреннего трения. Очевидно, что на тело, симметричное относительно направления скорости потока v, может действовать только лобовое сопротивление, подъемная же сила в этом случае будет отсутствовать.

Можно доказать, что в несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления. Этот результат получил название парадокса Даламбера.

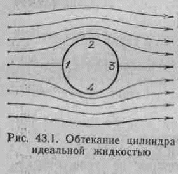
Покажем отсутствие лобового сопротивления на примере обтекания идеальной жидкостью очень длинного («бесконечного») цилиндра (рис. 43.1). Не обладая вязкостью, идеальная жидкость должна скользить по поверхности цилиндра, полностью обтекая его.

Поэтому линии тока будут симметричными как относительно прямой, проходящей через точки 2 и 3, так и относительно прямой, проходящей через точки 2 и 4. Теорема Бернулли позволяет по картине линий тока судить о давлении в разных точках потока. Вблизи точек 1 и 3 давление одинаково (и больше, чем в невозмущенном потоке, так как скорость вблизи этих точек меньше). Вблизи точек 2 и 4 давление также одинаково (и меньше, чем в невозмущенном потоке, так как скорость вблизи этих точек, больше) Следовательно, результирующая сил давления на поверхность цилиндра (которая в отсутствие вязкости могла бы обусловить лобовое сопротивление) будет равна нулю. Как уже отмечалось, такой же результат получается и для тел любой (в том числе и несимметричной) формы. Этот вывод касается только лобового сопротивления. Подъемная сила, равная нулю для симметричных тел (см., например, рис. 43.1), для несимметричных тел отлична от нуля.

На рис. 43.2 показаны линии тока при обтекании идеальной жидкостью полуцилиндра. Вследствие идеального обтекания линии тока несимметричны относительно прямой, проходящей через точки 2 и 4. Однако относительной прямой, проходящей через точки, 1 и 3 картина линий тока несимметрична. Вблизи точки 2 где линии гуще, давление меньше, чем вблизи дочки 4 , в результате чего возникает подъемная сила.

Иначе обстоит дело при движении тела в вязкой жидкости. В этом случае очень топкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за внутреннего трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него скоростью. Этот слой называется пограничным. В нем действуют силы вязкого трения, которые в конечном счете приложены к телу и приводят к возникновению лобового сопротивления.

Но влияние вязкости не исчерпывается возникновением сил трения. Наличие пограничного слоя в корне изменяет характер обтекания тела жидкостью.

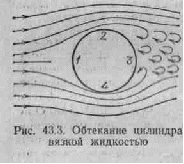
Полное обтекание становится невозможным. Действие сил трения в пограничном

слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри (рис. 43.3). Вихри уносится потоком и постепенно затухают вследствие трения; при этом энергия вихрей расходуется на нагревание жидкости. Давление в образующейся за телом вихревой области оказывается пониженным, вследствие чего результирующая сил давления отлична от нуля. Это в свою очередь обусловливает лобовое сопротивление.

Таким образом, как уже отмечалось, лобовое сопротивление слагается из сопротивления трения и сопротивления давления. При данных поперечных размерах тела сопротивление давления сильно зависит от формы тела. Наименьшим сопротивлением давления обладают тела хорошо обтекаемой каплевидной формы (рис. 43.4).

Соотношение между сопротивлением трения и сопротивлением давления определяется значением числа Рейнольдса (см. формулу (42.10)). В данном случае v — скорость тела относительно жидкости (или скорость потока, набегающего на тело), l — характерный размер тела, например радиус для тела шаровой формы. При малых Re (т. е. при малых v и l) основную роль играет сопротивление трения, так что сопротивлением давления можно пренебречь. С ростом вязкости относительная роль сил трения возрастает. По мере увеличения Re роль сопротивления давления все больше растет. При больших значениях Re в ло« бовом сопротивлении преобладают силы давления.

Определяя характер сил, действующих на тело в потоке жидкости или газа, число Рейнольдса служит критерием подобия и в этом случае. Это обстоятельство используется при моделировании. Например, модель самолета ведет себя в потоке газа так же, как и ее прообраз, если кроме геометрического подобия модели и самолета будет соблюдено равенство для них значений числа Рейнольдса.

Стокс установил, что при небольших скоростях и размерах тел (т. е. при малых Re, когда сопротивление среды обусловлено практически только силами трения), модуль силы сопротивления определяется формулой

Здесь n — динамическая вязкость среды, v — скорость движения тела, l — характерный размер тела, k — коэффициент пропорциональности, который зависит от формы тела. Для шара, если взять в качестве l его радиус r, коэффициент пропорциональности равен 6П.Следовательно, сила сопротивления движению в жидкостях небольших шариков при малых скоростях равна

Надо иметь в виду, что формула Стокса справедлива при условии, что расстояние от тела до границ жидкости (например, до стенок сосуда) много больше размеров тела.

Самолет поддерживается в воздухе подъемной силой, действующей на его крылья. Лобовое сопротивление играет при полете самолета вредную роль По этому крыльям и фюзеляжу самолета придают удобообтекаемую форму (рис. 43.5). Вследствие асимметричной формы и наклонного расположения крыла скорость воздуха над крылом оказывается больше (а, следовательно, давление меньше), чем под крылом. Благодаря этому создается подъемная сила. Существенную роль в образовании подъемной силы играет вязкость воздуха, которая обусловливает образование вихрей, отрывающихся от задней кромки крыла. Однако вникать в детали явлений, обусловливающих подъёмную силу, мы не имеем возможности .

Основы теории крыла самолета создал в 1904 г. Жуковский, который сформулировал теорему о подъемной силе и вывел формулу для определения этой силы, являющуюся основой всех аэродинамических расчетов самолетов.