Академия России

Кафедра Физики

Тема: «Нелинейные электрические цепи в режиме постоянного тока»

Орел-2009

Содержание

Нелинейные резистивные (безинерционные) двухполюсные и четырехполюсные элементы

Анализ нелинейных цепей с двухполюсными элементами

Графоаналитические методы анализа нелинейных цепей

Анализ цепей с четырехполюсными нелинейными элементами

Заключение

Литература

Нелинейные резистивные (безинерционные) двухполюсные и четырехполюсные элементы

Элемент электрической цепи, параметры которого зависят от значений токов и напряжений, называется нелинейным элементом (НЭ). Цепь, схема замещения которой не содержит реактивных элементов, называется безинерционной или резистивной. Термин “безинерционный” обусловлен тем, что в данных цепях переходный процесс заканчивается мгновенно.

При описании любого нового элемента электрической цепи устанавливается функциональная зависимость между напряжениями и токами на его зажимах, т.е. необходимо получит математическую модель элемента. Свойства нелинейных двухполюсных резистивных элементов описываются своей вольтамперной характеристикой (ВАХ), которую можно представить в виде

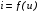
Для НЭ эта функция является нелинейной, например

,

или 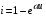и т.д.

Нелинейный четырехполюсник, как и линейный, описывается двумя уравнениями, которые связывают напряжения и токи на его входе и выходе. При анализе транзисторов часто используется следующая система уравнений:

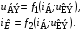
0

кэ



u

0

кэ



u

б

i

бэ

u

0

б

i

0

бэ

u

0

б



i

0

к

i

0

кэ

u

б0

i

0

б

б1

i

i



1

б

б2

i

i



к

i

кэ

u

кэ

u



А

А

бэ

u



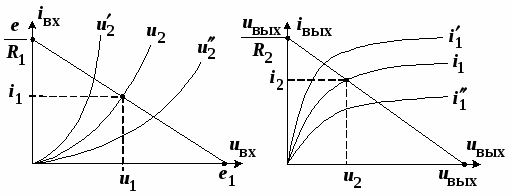
Графическое изображение уравнений для транзистора (входная и выходная характеристики) в схеме с общим эмиттером показано на рис. 1.1.

Рис. 1.1.

Для резистивных НЭ важным параметром является их сопротивление, которое зависит от того, в какой точке ВАХ оно определяется. Различают два вида сопротивлений: статическое и динамическое. Статическое сопротивление 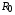в рабочей точке А (рис. 1.1) определяется как

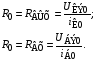
Это сопротивление постоянному току, оно характеризуется тангенсом угла наклона прямой, проходящей через рабочую точку А и начало координат.

Под действием напряжения малой амплитуды:

,

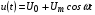ток повторит по форме напряжение:

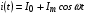, т.е.

переменное напряжение 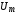и амплитуда переменного тока .

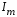Для определения динамического (дифференциального) сопротивления 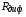по выходной характеристике НЭ необходимо выбрать приращение 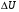и и 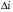определить динамическое следующим образом:

.

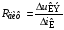Это сопротивление представляет собой сопротивление НЭ переменному току малой амплитуды.

Обычно переходят к пределу этих приращений и определяют дифференциальное сопротивление в виде:

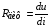
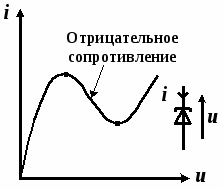
Различают нелинейные элементы с монотонной и немонотонной ВАХ. Нелинейные элементы с немонотонной ВАХ имеет падающие участки и называется НЭ с отрицательным сопротивлением. Типичным НЭ с немонотонной ВАХ является тунельный диод (рис. 1.2)

Рис. 1.2.

В заключение отметим, что в теории нелинейных цепей не изучаются устройства НЭ, а используются внешние характеристики (модели) подобно тому, как при изучении теории линейных цепей не рассматривают устройство резисторов, конденсаторов и катушек и пользуются только их математическими моделями с параметрам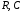и и .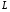

Анализ нелинейных цепей с двухполюсными элементами

Составление уравнений состояния цепи на основании законов Кирхгофа.

По первому закону Кирхгофа записываются уравнения вида:

,

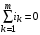где m – число ветвей, сходящихся в узле.

По второму закону Кирхгофа записываются уравнения вида:

,

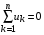где n – число ветвей, входящих в контур.

Если цепь содержит, кроме линейных, также НЭ, то в системе уравнений, описывающей состояние цепи появятся уравнения вида 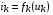. Методика составления уравнений состояния цепи на основе законов Кирхгофа остается такой же, как в случае линейных резистивных цепей.

Составим, например, систему уравнений состояния для цепи, схема которой изображена на рис. 1.3. Пусть ВАХ нелинейного элемента определена выражением:

.

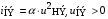Рис. 1.3.

Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур и один независимый узел. Уравнения, записанные по законам Кирхгофа, имеют следующий вид:

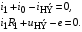
К этим уравнениям дописываем уравнение 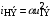. Неизвестными в данной системе уравнений являются напряжение 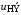и ток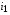и и . Всего три неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс составления системы уравнений такой же, как и в случае линейной цепи. Однако процесс решения полученной системы, которая содержит нелинейное уравнение, может существенно затрудниться. Для большинства относительно сложных цепей аналитического решения системы уравнений может и не существовать. Тогда приходится прибегать к численным методам решения.

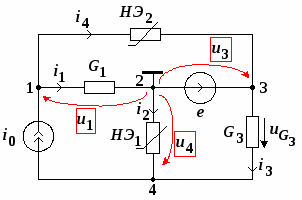
Составление уравнений состояния цепи методом узловых напряжений.

Рассмотрим в качестве примера схему, изображенную на рис. 1.4. Пусть ВАХ нелинейных элементов описываются выражениями

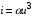для НЭ₁ и 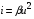для элемента НЭ₂.

Рис. 1.4.

Приняв узел 2 за базисный, имеем три независимых узла, но уравнения будем составлять для 1 и 4 узлов. Узловое напряжение 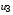известно 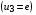. Токи ветвей выражаются через узловые напряжения и следующим образом:

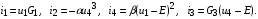
Составим уравнения для узлов 1 и 4 по первому закону Кирхгофа:

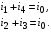
Подставив в эти уравнения значения токов, получим:

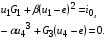
Уравнения узловых напряжений получены в виде системы двух нелинейных уравнений с двумя неизвестными узловыми напряжениями.

Решить данную систему уравнений можно одним из численных методов (например, известным из математики методом Ньютона-Рафсона). Определив узловые напряжения, можно вычислить токи и напряжения ветвей.

Графоаналитические методы анализа нелинейных цепей

Сущность графоаналитических методов состоит в том, что путем подстановки систему уравнений сводят к системе, состоящей из двух уравнений от двух неизвестных. Потом эти уравнения изображают на графике. Точка пересечения графиков даст искомое решение.

Данные методы используются также в случаях, когда ВАХ нелинейного элемента задана графически и получить аналитическое выражение для нее затруднено (ВАХ описывается сложной функцией).

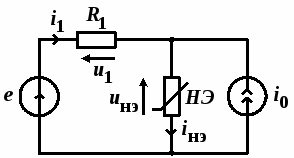
Для демонстрации графоаналитического метода решим следующую систему уравнений для схемы на рисунке 1.3:

1

R

НЭ

0

i

e

1

u

нэ

U

нэ

i

1

i

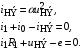
Из второго уравнения выразим ток 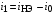и подставим его в третье уравнение. В результате этой операции получим:

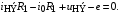
Решим уравнение относительно тока в НЭ:

.

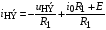Это уравнение прямой 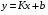, где .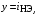

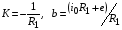Точка пересечения ВАХ нелинейного элемента 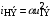и уравнения прямой дает решение задачи.

Метод эквивалентного генератора

Если цепь содержит один НЭ, то применяют метод эквивалентного генератора. При этом линейная цепь относительно зажимов НЭ заменяется эквивалентным генератором напряжения или тока (рис. 1.5).

2-х

пол-к

НЭ



хх

u

нэ

i

НЭ

э

R

нэ

u



НЭ

э

R

нэ

i

кз

i

нэ

u

(a) (б) (в)

Рис. 1.5.

Ток в НЭ и напряжение на нем находится из системы, состоящей всего из двух уравнений. Так, применяя второй закон Кирхгофа к схеме рис. 1.5, б получаем:

.

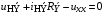Дописывая к данному равенству уравнение НЭ 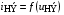, получаем систему из двух уравнений. Решить данную систему можно графическим путем, построив график прямой:

.

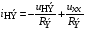и график ВАХ 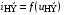нелинейного элемента. Точка пересечения графиков дает значение тока и напряжения на НЭ.

Эквивалентное преобразование схем с нелинейными элементами

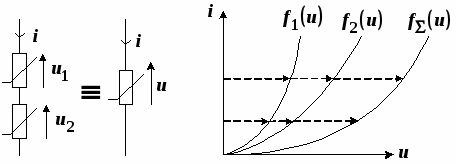
Суть эквивалентных преобразований состоит в замене участков цепи с параллельным или последовательным соединением ветвей одной эквивалентной ветвью путем суммирования их токов или напряжений по заданным характеристикам ветвей цепи.

Пусть два НЭ с уравнениями (ВАХ) 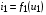и 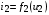включены параллельно (рис. 1.6).

Необходимо найти уравнение НЭ, эквивалентного данному соединению элементов. Так как элементы соединены параллельно, то 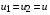, а по первому закону Кирхгофа 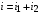. Выполним сложение токов графически, как показано на рис. 1.7.

Рис. 1.6. Рис. 1.7.

Задаемся значением напряжения. При этом значении напряжения находим токи НЭ и суммируем их. Задаемся новым значением напряжения и опять суммируем токи. Таким образом, находим серию точек, соединяя которые, получаем ВАХ эквивалентного НЭ.

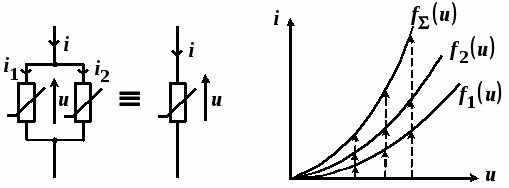
Рассмотрим последовательное соединение НЭ (рис. 1.8).

Рис. 1.8. Рис. 1.9.

В данном случае 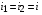, а 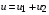. Процесс определения ВАХ НЭ показан на рис. 1.9. Заметим, что рассмотренные преобразования применимы и в случае, когда последовательно или параллельно соединены несколько линейных, а также нелинейных элементов.

Поочередное применение правил эквивалентного преобразования участков с последовательным и параллельным соединением элементов позволяет постепенно "свертывать" участки цепей со смешанным соединением линейных и нелинейных сопротивлений с монотонными ВАХ.

Цепи, состоящие из линейных и нелинейных сопротивлений, можно использовать для стабилизации напряжения.

Отношение относительного приращения напряжения на входе таких цепей к относительному приращению выходного напряжения называется коэффициентом стабилизации.

.

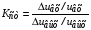Следует подчеркнуть, что эффект стабилизации напряжения в принципе не может иметь места в цепях, составленных из элементов с линейными ВАХ.

Вопрос к аудитории: Может ли иметь место стабилизация в линейных цепях?

Анализ цепей с четырехполюсными нелинейными элементами

Рассмотрим анализ резистивных цепей, если в их состав входят нелинейные четырехполюсники, которые описываются нелинейными уравнениями. На рис. 1.10 показана схема включения нелинейного четырехполюсника, а на рис. 1.11 – семейство его входных (а) и выходных (б) ВАХ.

Рис. 1.10.

Рис. 1.11.

По второму закону Кирхгофа для входной и выходной цепей схемы 1.10 можно записать:

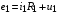и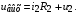

Решая эти уравнения относительно токов 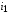и 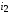получаем уравнения:

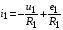и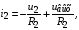

которые называются уравнениями нагрузочных прямых.

На рис. 1.11 построены графики этих прямых и графических входных и выходных ВАХ четырехполюсного НЭ. Точки пересечения нагрузочных прямых и ВАХ определяют режимы постоянного тока (рабочие точки) на входе и выходе четырехполюсного НЭ.

Заключение

В подавляющем большинстве практических задач анализа нелинейных резистивных цепей конфигурация цепи не бывает произвольно сложной; в цепи, как правило, действует один источник переменного сигнала, и требуется определить реакцию в одной или двух ветвях. Задача анализа сводится к следующему: при заданной цепи, содержащей резистивные элементы с известными характеристиками, источники постоянного напряжения и тока и один источник переменного сигнала 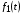, действующий на входе, определить реакцию 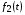: напряжение или ток на входе, либо на выходе цепи. Точное аналитическое решение задачи анализа возможно только в редких случаях простейших резистивных цепей с определенными характеристиками элементов. Уравнения электрического равновесия решают приближенными численными, графическими или графо-аналитическими методами.

Литература

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.

2. Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.

3. Качанов Н.С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974.

4. В.П. Попов Основы теории цепей – М.: Высшая школа, 2000