Определение момента инерции тела и проверка теоремы Штейнера методом крутильных колебаний
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА И ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ.
Цель работы: изучить метод крутильных колебаний (трифилярный подвес) и применить его для определения момента инерции тела и проверки теоремы Гюйгенса-Штейнера.
Приборы и принадлежности: установка, секундомер, штангенциркуль, линейка, образцы для измерений.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ УСТАНОВКИ.
Установка для определения момента инерции тела, которая применяется в данной работе, называется трифилярным подвесом. Состоит она из диска (платформы) (рис.1), горизонтально подвешенной на трех симметрично расположенных нитях 2. Вверху нити прикреплены к основанию 3, имеющему три симметрично расположенных выступа. Основание с помощью болта 5 и упругой пластины 6 соединено с кронштейном 4.
Платформа может совершать крутильные колебания вокруг вертикальной оси, проходящей через ее середину. При этом центр тяжести платформы перемещается вдоль оси вращения.
Пусть масса платформы m0, вращаясь в некотором направлении, поднялась на высоту h от положения равновесия. Изменение ее потенциальной энергии при этом составит
E1=m0gh (1)
где g – ускорение силы тяжести.
Возвратившись в положение равновесия, платформа будет иметь угловую скорость 0 и кинетическая энергия ее будет
E2=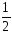 I
I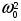 (2)
(2)
где I – момент инерции платформы относительно оси вращения.
Пренебрегая работой сил трения, закон сохранения механической энергии запишется
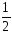 I
I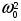 = m0gh (3)
= m0gh (3)
При малой амплитуде колебания платформы будут гармоническими, т.е. зависимость углового смещения от времени t имеют вид
=sin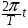 (4)
(4)
где - амплитуда;
Т – период колебаний.
В свою очередь угловая скорость =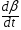 или =
или =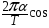
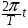 . Максимальное изменение угловой скорости 0 , соответствующее моменту времени, когда платформа проходит через положение равновесия
. Максимальное изменение угловой скорости 0 , соответствующее моменту времени, когда платформа проходит через положение равновесия
=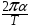 (5)
(5)
Из (3) и (5) имеем
mgh=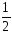 I(
I(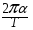 )² (6)
)² (6)
Найдем h. Пусть l – длина нитей подвеса (рис.2), R – расстояние от центра платформы до точек крепления нитей на ней, r – радиус окружности, на которой лежат точки крепления нитей к основанию.
Из рис.2 видим, что
h=OO1=BC-BC1=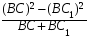
В свою очередь 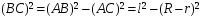
Поэтому 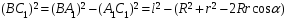
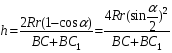
При малых углах смещения
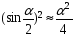 ; (BC+BC1)=2l
; (BC+BC1)=2l
учитывая это, будем иметь
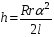 (7)
(7)
тогда из (6) и (7) находим
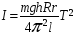 (8)
(8)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
Упражнение 1. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА.
Убедиться в том, что платформа расположена горизонтально.
Определить R,r,l (масса платформы m0=(1.0250.0005)кг.), R и r удобно определить из известной геометрической формулы, измерив предварительно с помощью линейки расстояние между точками подвеса двух нитей вверху и внизу.
Путем несильного нажатия на край основания 3 (рис.1) сообщить платформе вращательный импульс и при помощи секундомера измерить время 50-70 полных ее колебаний. Опыт повторить 3-5 раз.
Найти период Т0 из этих этих колебаний по формуле (8) определить I0 – момент инерции платформы. Результаты занести в таблицу 1.
Платформу нагрузить исследуемым телом, предварительно определив его массу m. Определить период колебаний T1 системы тело-платформа (масса системы – m+m0) и момент инерции системы I1. Величина момента инерции тела найдется как разница I=I1-I0. Опыт повторить 3-5 раз. Результаты измерений занести в таблицу 2.
Найти ошибку определения I.
Сравнить полученное значение I и I0с теоретическим, вычисленным по формуле момента инерции для данного тела.
Упражнение 2: ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА- ШТЕЙНЕРА (ШТЕЙНЕРА-ЖУРАВСКОГО).
Взять два одинаковых тела и в соответствии с упражнением 1 определить их момент инерции 2I2. Для этого, положив тела одно на другое в центре платформы так, чтобы центры масс тел лежали на одной вертикали с центром масс платформы. Момент инерции одного тела относительно проходящей через центр масс оси будет равен I2. Опыт повторить 3-5 раз. Результаты занести в таблицу 3.
Расположить тела на некотором расстоянии друг от друга симметрично относительно центра платформы.
Определить расстояние a от центра масс из тел до оси вращения и его момент инерции I3. Из опыта найти момент инерции системы из двух тел 2I3. Опыт повторить 3-5 раз. Результаты измерений занести в таблицу 4.
Найти I3 по теореме Штейнера
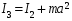 (9)
(9)
где m – масса тела, при этом для I2, m, a берут значения,
полученные опытным путем.
Сравнить значения I3, полученные по формуле (9) и экспериментально.
Найти ошибки определения I2 и I3.
Таблица 1.
№
п/п
R
м
r
м
l
м
m0
кг
N
t
c
T0
c
I0
кг*м²
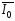
кг*м²
I0
кг*м²
Таблица 2.
№
п/п
R
м
r
м
N
t
c
T1
c
I+I0
кг*м²
I
кг*м²
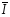
кг*м²
I
кг*м²
Таблица 3.
№
п/п
m
кг
(m+m0)
кг
N
t
c
T
c
(2I2+I0)
кг*м²
I2
кг*м²
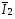
кг*м²
I2
кг*м²
Таблица 4.
№
п/п
m
кг
(m+m0)
кг
а
м
N
t
c
T
c
(2I3+I0)
кг*м²
I3
кг*м²
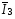
кг*м²
I3
кг*м²
Масса большого цилиндра mб=(842,50,5)г.
Масса малого цилиндра mм=(303,150,5)г.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ