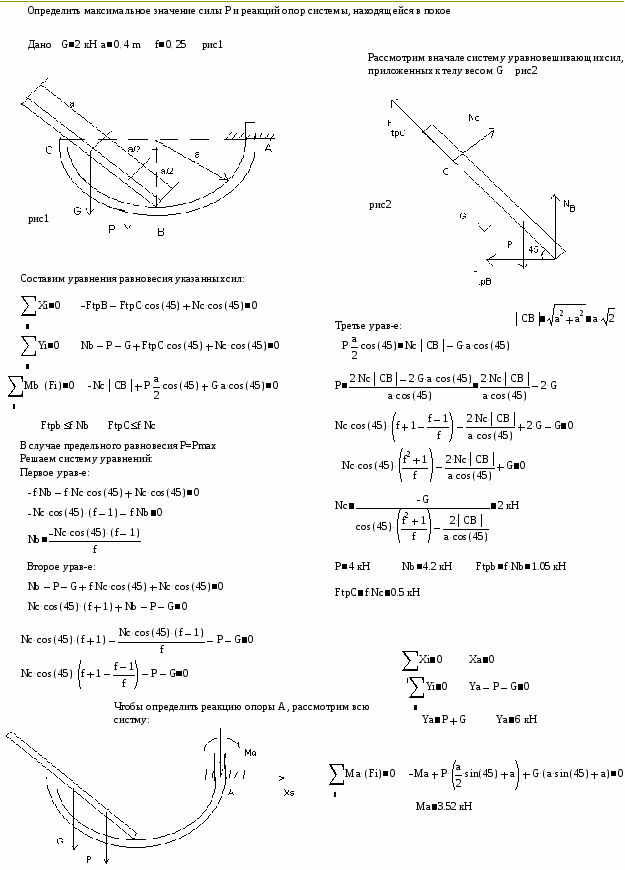
Определение реакций опор составной конструкции






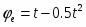
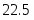
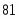
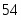
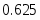
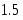
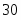
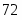
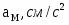
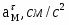
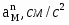
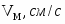
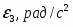
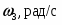
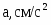
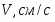
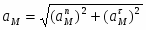
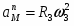
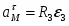
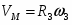
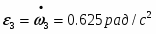
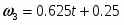
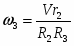
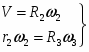
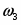
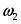
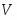
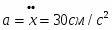
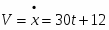
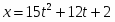
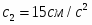
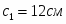
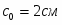
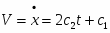
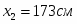
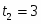
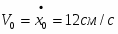
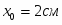
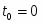
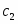
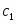
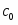
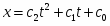
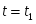
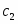
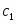
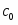
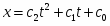
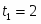
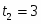
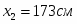
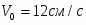
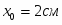
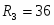
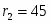
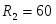
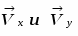
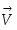
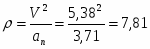
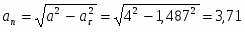
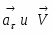
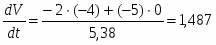
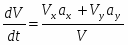
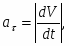
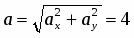
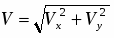
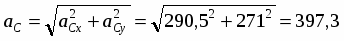
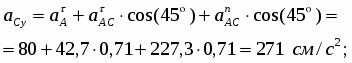
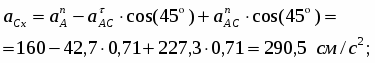
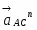
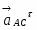
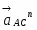
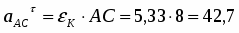
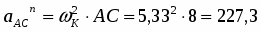
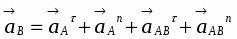
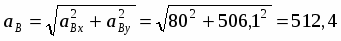
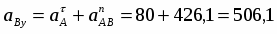
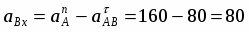
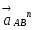
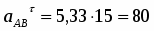
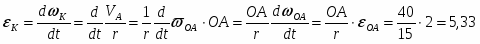
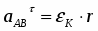
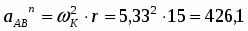
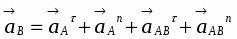
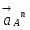
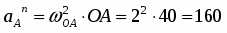
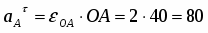
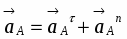
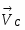
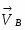
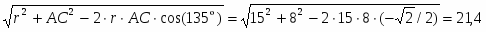
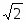
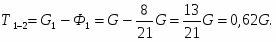
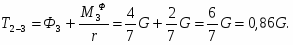
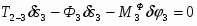
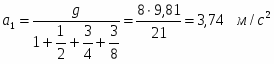
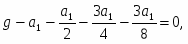
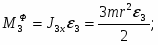
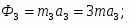
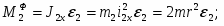
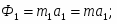
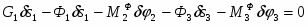
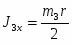
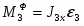
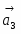
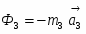
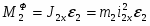

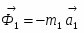
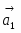
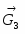
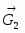
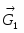
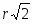
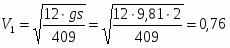
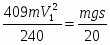
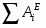
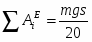
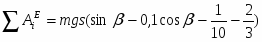
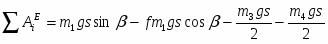
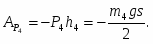
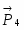
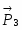
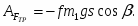
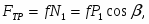
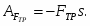
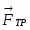
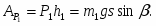
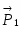
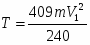
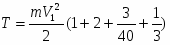
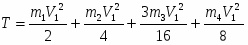
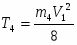
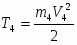
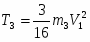
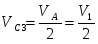
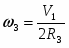
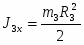
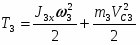
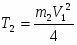
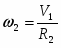
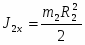
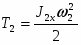
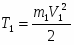
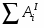
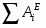
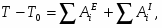
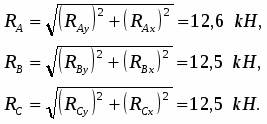
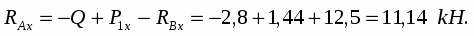
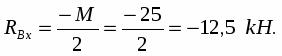
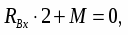
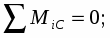
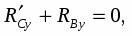
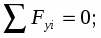
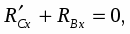
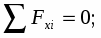
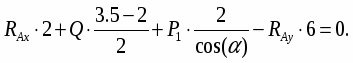
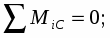
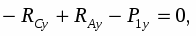
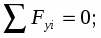
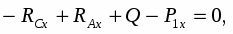
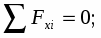
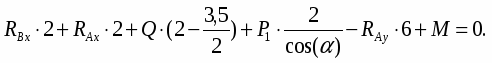
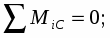
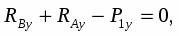
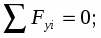
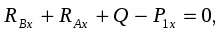
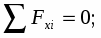
 Задание С-3. Определение реакций опор составной конструкции
Задание С-3. Определение реакций опор составной конструкции
Вариант № 1.
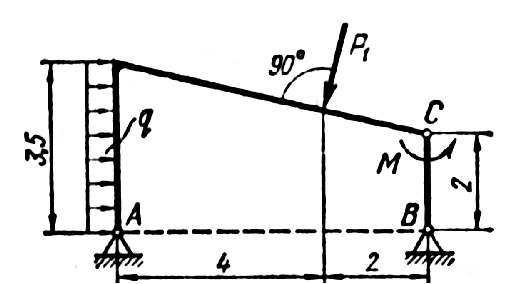
Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схема конструкции представлена на рис. 1 (размеры – в м), нагрузка указана в таблице 1.
Рис. 1
Таблица 1.
-
P1, кН
М, кНм
q, кН/м
6,0
25,0
0,8
С-3. Определение реакций опор составной конструкции
Решение. Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис. 2).
y
P1y P1
90
P1x C
Q M
RAy RBy
RAx RBx x
A B
Рис. 2.
Разложим силу P на составляющие Px и Py.
P1y P1
P1x
6
Рис. 3.
P1x = P1sin(),
P1y = P1cos().
= arctg(1,5/6) = arctg(0,25) = 14.
P1x = P1sin() = P1sin(14) = 60,24 = 1,44 (кН),
P1y = P1cos() = P1cos(14) = 60,97 = 5,82 (кН).
Q = q3,5 = 0,83,5 = 2,8 (кН).
С-3. Определение реакций опор составной конструкции.
Запишем уравнения равновесия:
(1)
(2)
(3)
Данная система из 3 уравнений содержит 4 неизвестных, для их нахождения рассмотрим отдельно правую и левую части конструкции.
Рассмотрим систему уравновешивающихся сил, приложенных к левой части конструкции (рис.4):
y
P1y P1
90
P1x C
RCx
Q RCy
RAy
RAx x
A
Рис. 4.
Запишем уравнения равновесия:
(4)
(5)
С-3. Определение реакций опор составной конструкции
(6)
Рассмотрим систему уравновешивающихся сил, приложенных к правой части конструкции (рис.5):
y
R`Cy
R`Cx
C
M
RBy
RBx x
B
Рис.5.
Запишем уравнения равновесия:
(7)
(8)
(9)
где RCx = R`Cx, RCy = R`Cy.
Таким образом, имеем систему 4 уравнений (1), (2), (6) и (9) с 4 неизвестными.
Из уравнения (9)
Из уравнения (1)
С-3. Определение реакций опор составной конструкции
Из уравнения (6)
Из уравнения (2)
Найдем реакции шарнира С:
RCx = -RBx = 12,5 кН,
RCy = -RBy = 0,07 кН.
Отрицательные значения RBx и RBy говорят о том, что действительное направление RBx и RBy противоположно указанному на рис.4.
Итак,
С-3. Определение реакций опор составной конструкции
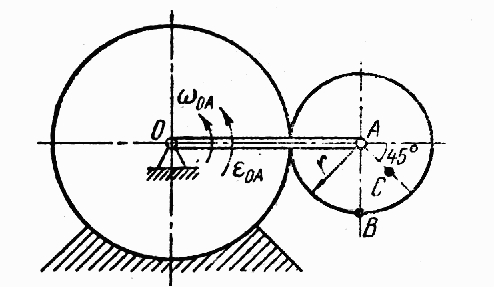
Найти реакции опор конструкции изображенной на рис.1.
Дано: Q = 2, G = 20, a = 20, b = 30,
c = 10 R =15, r =5.
Решение:
Разложим реакции в опорах А и Б на их составляющие по осям коардинат, при этом RAy=RBy=RDy=0
RAx
RBx
P
qx
x
y
450 z
P
RBz
RAz
q
G
RDz
Q
x
RAz
RBz
qz
z
y
G
Составим уравнения сумм моментов относительно всех осей:
Р*15-q*5=0, где , отсюда Р=(q*5)/15
-qx*20+P*60-RBx*80, отсюда RBx=(qx*20-P*60)/80
-qx*20-G*(20+30)+RBz*(20+30+30) отсюда RBz= (qx*20+G*50)/80
-Raz*80+qz*60+G*30=0 отсюда Raz= (qz*60+G*30)/80
Rax*80+ qx*60-P*30=0 отсюда Rax=-( qx*60-P*30)/80
qx=Q*cos45; qz=Q*sin45
Ra= RB=
Результаты работы
Raz
Rax
Ra
RBz
RBx
RB
Применение теоремы об изменении кинетической энергии к изучению движения механической системы.
Вариант № 1.
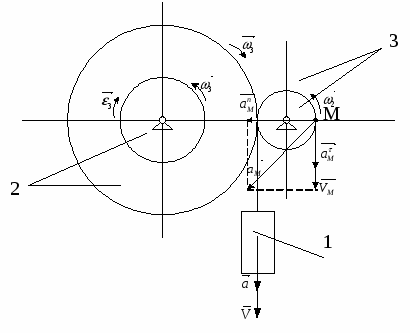
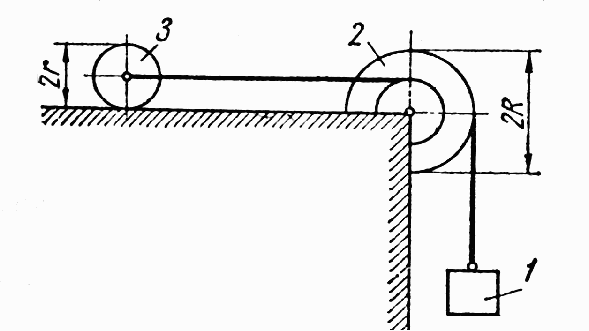
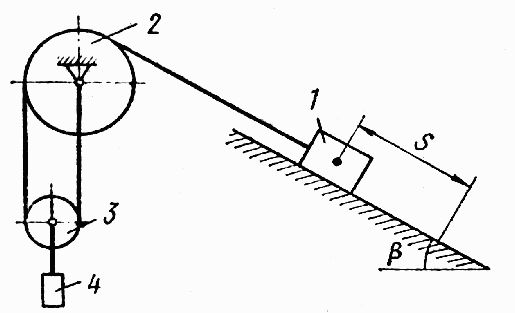
Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рис. 1. Учитывая трение скольжения тела 1, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; - угол наклона плоскости к горизонту; f – коэффициент трения скольжения.
Необходимые для решения данные приведены в таблице 1. Блоки и катки считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Рис. 1
Таблица 1.
m1, кг
m2, кг
m3, кг
m4, кг
, град
f
s, м
m
4m
0,2m
4m/3
60
0,10
2
Решение.
Применим теорему об изменении кинетической энергии системы:
(1)
где T0 и T – кинетическая энергия системы в начальном и конечном положениях; - сумма работ внешних сил, приложенных к системе; - сумма работ внутренних сил системы.
Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями,
Так как в начальном положении система находится в покое, то Т0=0.
Следовательно, уравнение (1) принимает вид:
(2)
Кинетическая энергия рассматриваемой системы Т в конечном ее положении (рис.2) равна сумме кинетических энергий тел 1, 2, 3 и 4:
Т = Т1 + Т2 + Т3 + Т4. (3)
2
1
2
VA
V3
3 V1
A C3 CV
3
V4
4
Рис. 2.
Д-10
Кинетическая энергия груза 1, движущегося поступательно,
(4)
Кинетическая энергия барабана 2, совершающего вращательное движение,
, (5)
где J2x – момент инерции барабана 2 относительно центральной продольной оси:
, (6)
2 – угловая скорость барабана 2:
. (7)
После подстановки (6) и (7) в (5) выражение кинетической энергии барабана 2 принимает вид:
. (8)
Кинетическая энергия барабана 3, совершающего плоское движение:
, (9)
где VC3 – скорость центра тяжести С3 барабана 3, J3x – момент инерции барабана 3 относительно центральной продольной оси:
, (10)
3 – угловая скорость барабана 3.
Так как двигается по нити без скольжения, то мгновенный центр скоростей находится в точке СV. Поэтому
, (11)
. (12)
Подставляя (10), (11) и (12) в (9), получим:
. (13)
Кинетическая энергия груза 4, движущегося поступательно,
, (14)
где V4 = VC3 = V1/2:
. (15)
Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (4), (8), (13), (15):
Подставляя и заданные значения масс в (3), имеем:
или
. (16)
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении (рис. 3).
2
1
N1
FTP
3
C3
P3 P1
4
P4
Рис. 2.
Работа силы тяжести :
(17)
Работа силы трения скольжения :
Так как
то
(18)
Работа силы тяжести , препятствующей движению тела 1:
(19)
Работа силы тяжести , препятствующей движению тела 1:
(20)
Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (17) – (20):
.
Подставляя заданные значения масс, получаем:
или
. (21)
Согласно теореме (2) приравняем значения Т и , определяемые по формулам (16) и (21):
,
откуда
м/с.
Д-10
Задание Д-19. Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы.
Вариант № 1.
Для заданной механической системы определить ускорения грузов и натяжения в ветвях нитей, к которым прикреплены грузы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.
Необходимые для решения данные приведены в таблице 1. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.
Рис. 1
Таблица 1.
G1, кг
G2, кг
G3, кг
R/r
i2x
G
G
3G
2
Решение.
Применим к решению задания общее уравнение динамики. Так как система приходит в движение из состояния покоя, направления ускорений тел соответствуют направлениям их движения. Движение таково, что груз 1 опускается.
Покажем задаваемые силы: силы тяжести - груза 1, - блока 2 и - катка 3 (рис. 2).
a3
M3Ф 2 2 M3Ф
Ф3 3 3
2
s3
3
G3
Ф1
G2 1
a1
s3
G1
Рис. 2.
Приложим силы инерции. Сила инерции груза 1, движущегося поступательно с ускорением :
.
Силы инерции блока 2, вращающегося вокруг неподвижной оси с угловым ускорением 2, приводятся к паре, момент которой
Силы инерции катка 3, совершающего плоское движение, приводятся к силе
,
где - ускорение центра масс катка 3, и к паре сил, момент которой
,
где 3 – угловое ускорение катка 3, J3 – момент инерции катка 3 относительно центральной продольной оси:
.
Сообщим системе возможное перемещение в направлении ее действительного движения (рис. 2). Составим общее уравнении динамики:
, (1)
где 2 и 3 – углы поворотов блоков 2 и 3.
Учитывая, что G1 = G2 = G = mg, G3 = 3G = 3mg
имеем:
(2)
Устанавливаем зависимости между возможными перемещениями, входящими в (1), и между ускорениями в (2), пользуясь тем, что эти зависимости такие же, как между соответствующими скоростями:
2 = 3 = s1/R = s1/2r;
s3 = 2r = s1/2; (3)
2 = 3 = a1/2r; a3 = a1/2.
С учетом (2) и (3) уравнение (1), после деления всех его членов на m и s1, принимает вид
откуда
,
а3 = a1/2 = 1,87 м/с2.
а3
M3Ф
Ф3 3 3 Т2-3
s3
G3
Рис. 3.
Ф1
Т1-2
а1
s1
G1
Рис. 4.
Для определения натяжения в нити 2-3 мысленно разрежем эту нить и заменим ее действие на каток 3 реакцией T2-3 (рис. 3).
Общее уравнение динамики:
,
откуда
Для нахождения натяжения в нити 1-2 мысленно разрежем эту нить и заменим ее действие на груз 1 реакцией T1-2 (рис. 4).
Не составляя общего уравнения динамики, на основании принципа Даламбера имеем:
Задание К-3. Определение скоростей и ускорений точек твердого тела при плоском движении.
Вариант № 1.
Рис. 1
Найти для заданного положения механизма скорости и ускорения точек В и С. Схема механизма представлена на рис. 1, необходимые для расчета данные приведены в таблице 1.
Таблица 1.
-
Размеры, см
ОА, с-1
ОА, с-2
ОА
r
АС
40
15
8
2
2
Решение.
Определение скоростей точек.
Вычислим скорость точки А при заданном положении механизма:
VA = ОАOA = 240 = 80 см/с.
Скорость точки А направлена перпендикулярна к ОА. Мгновенный центр скоростей СV находится в точке соприкосновения колес.
Угловая скорость колеса
К = VA/r = 80/15 = 5,33 c-1
Скорости точек В и С:
VB = КВСV;
VС = КССV,
где
ВСV = r= 151,41 = 21,2 см,
ССV = см.
Следовательно,
VB = КВСV = 5,3321,2 = 113 см/с;
VС = КССV = 5,3321,4 = 114,1 см/с.
Вектор направлен перпендикулярно к отрезку BCV, а вектор - перпендикулярно к отрезку CCV в сторону вращения колеса.
VA
VC
К
O OA CV A VB
45
C
r
B
Рис. 2
К-3
Определение ускорений точек.
Ускорение точки А складывается из вращательного и центростремительного ускорений:
;
см/с2;
см/с2.
Вектор направлен от А к О. Вектор перпендикулярен к вектору и направлен в соответствии с направлением углового ускорения ОА.
Согласно теореме об ускорениях точек плоской фигуры имеем:
.
Центростремительное ускорение точки В во вращательном движении колеса вокруг полюса А:
см/с2.
Вращательное ускорение точки В:
,
где
с-2,
см/с2.
Вектор направлен от В к А. Вектор перпендикулярен к вектору и направлен в соответствии с направлением углового ускорения K.
Ускорение точки В находим способом проекций:
см/с2;
см/с2;
см/с2.
Определяем ускорение точки С:
.
Центростремительное ускорение точки С во вращательном движении колеса вокруг полюса А:
см/с2.
К-3
Вращательное ускорение точки С:
см/с2.
Вектор направлен от С к А. Вектор перпендикулярен к вектору и направлен в соответствии с направлением углового ускорения K.
Ускорение точки С находим способом проекций:
см/с2.
y
aC aCy
aBy
aB
aA
OA K aAC
x O aAn A
aACn
C
aCx 45
aABn
aBx B aAB
Рис. 3
К-3
Задание K-1. Определение скорости и ускорения точки по заданным уравнениям ее движения.
Вариант № 1.
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1(c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке. Данные приведены в таблице 1.
Таблица 1.
-
Уравнения движения
t1(c)
x = x(t), см
y = y(t), см
-2t2+3
-5t
0,5
K-1
Решение.
Исходные данные в см и с:
x = -2t2 + 3; y = -5t; (1)
t1 = 0,5
Уравнения движения (1) являются параметрическими уравнениями траектории точки М. Чтобы получить уравнение траектории в обычной координатной форме, исключим время t из уравнений движения. Тогда
25x + 2y2 = 75 (2)
Это уравнение параболы.
Для определения скорости точки находим проекции скорости на оси координат:
Vx = x’ = -4t см/с; Vy = y’ = -5 см/с.
Модуль скорости точки
. (3)
Аналогично проекции ускорения точки
ax = x’’ = -4 см/с2; ay = y’’ = 0.
Модуль ускорения точки
см/с2.
Касательное ускорение находим путем дифференцирования модуля скорости (3)
При t = 0,5 c
x = -20,52 + 3 = 2,5 см, y = -50.5 = -2,5 см.
Vx = -40,5 =-2 см/с, Vy = -5 см/с, V = 5,38 см/с.
ax = -4 см/с2, ay = 0, a = 4 см/с2
см/с2
K-1
Модуль касательного ускорения
a = 1,487 см/с2
Знак “+” при dV/dt показывает, что движение точки ускоренное и, следовательно, направления совпадают.
Нормальное ускорение точки:
см/с2.
Радиус кривизны траектории в той точке, где при t = 0,5 с находится точка М:
см.
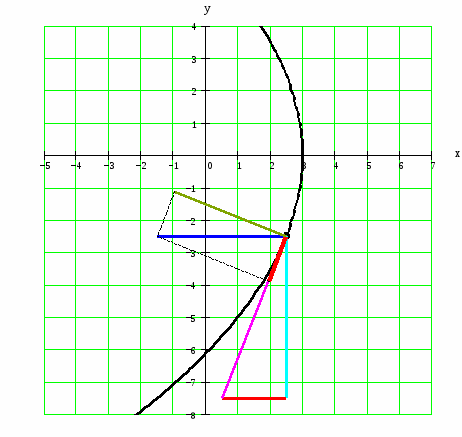
Пользуясь уравнением (2), строим траекторию (рис. 1) и показываем на ней положение точки М в заданный момент времени. Вектор строим по составляющим , причем он направлен по касательной к траектории точки. Вектор находим как по составляющим , так и по .
Рис. 1
Задание К-2. Определение скоростей и ускорений точек твёрдого тела при поступательном и вращательном движениях.
Вариант № 1.
Дано:
Определить коэффициенты , и , при которых осуществляется требуемое движение груза 1. Определить так же в момент времени скорость и ускорение груза и точки М одного из колёс механизма.
Решение:
Уравнение движения груза 1 имеет вид:
(1).
Коэффициенты , и могут быть определены из следующих условий:
при (2).
при (3).
Скорость груза 1:
(4).
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты:
Таким образом уравнение движения груза 1:
(5).
Скорость груза 1:
(6).
Ускорение груза 1:
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза и угловые скорости колёс и .
В соответствии со схемой механизма
(7).
откуда
или с учётом (6) после подстановки данных:
Угловое ускорение колеса 3:
Скорость точки М, её вращательное, центростремительное и полное ускорения определяются по формулам:
Выполнил: ст.гр. С-045 rus Калайчиди Виктор
Проверил: Русу В.Н.
-
Шифр
Вариант
61
16
Дано: схема механизма,
Sr=OM=20 sin рt см
t1=1/3 c
a=20 cм
Решение:
Положение М на фигуре D определяется расстоянием Sr=OM
При t=1/3 c
Sr=20 sin р/3 =17.32 cм
Абсолютная скорость точки М
V=Vr+Ve
Модуль относительной скорости
Vr=| Vr |
Vr=dSr/dt=20р cos рt
При t=1/3 c
Vr=10 р=31.41 cм/с
Положительный знак у величины Vr показывает, что вектор Vr направлен в сторону возрастания Sr
Модуль переносной скорости
Ve=Rщe
R= Sr2+a2 =26.46 см
щe=|щe| щe=dцe/dt=1-t c-1
При t=1/3
щe= 0.67 c-1
Положительный знак у величины щe показывает, что вращение фигуры D происходит вокруг Оz по направлению отсчета угла ц. Вектор щe направлен на наблюдателя.
Переносная скорость
Ve=17.73 см/с
Вектор Ve направлен по касательной к окружности вращения т.М
Из теоремы косинусов найдём
V=Vr2+ Ve2 - 2VrVeсos б
cos б = a/R = 0.76
V=21.32 cм/с
Абсолютное ускорение точки равно геом. сумме относительного, переносного, и кориолисова ускорений
W=Wr+We+Wc
W=Wrф+Wrn+Weв +Weц+Wc
Wrф= d2Sr/dt2 =-20р2 sin рt
При t=1/3 c
Wrф= -170.77 cм/с2
Wrф=170.77 cм/с2
Знак “-“ показывает, что Wrф направлен в сторону убывания Sr
Wrn=Vr2/с=0 (с=∞)
Модуль переносного вращательного ускорения
Weв=Rеe
еe= d2цe/dt2=-1 c-2
Weв= -26.46 cм/с2
Разные знаки у величин еe и щe говорят о замедленном движении круга D, вектора еe и щe противоположно направленны.
Weц=R щe2=11.88 cм/с2
Вектор Weц направлен к центру окружности L
Wc=2щe x Vr
Wc=2щeVr sin(щe Vr)
sin(щe Vr)=1
Wc=2щeVr=48.09 cм/с2
По методу проекций имеем
Wx= Weв cos б - Weц cos(90-б) - Wrф=
Wy= Wc-Weв sin б - Weц sin(90-б) =
W= Wx2+ Wy2=
щe, c-1
Скорость, см/с
еe,c-2
Ускорение, см/с2
Vr
Ve
V
Wrф
Wrn
Weв
Weц
Wc
Wx
Wy
W
0.67
31.41
17.73
21.32
-1
-170.77
0
-26.46
11.88
48.09

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ