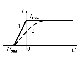
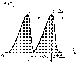
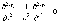
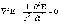
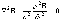
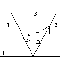
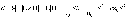
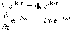
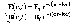
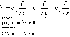
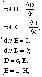
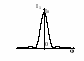
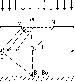
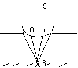
13. Ддифракция на круглом отверстии

вид дифракционной картины в точке В, зависит от числа зон Френеля, которые укладываются на открытой части волнового фронта.

Число действующих зон Френеля в точке В будет чётным или нечётным в зависимости от размера отверстия и от длины волны.

Амплитуда в точке В: А_В , возбуждаемая всеми зонами, определяется как: А_В=А₁/2  Am/2 , где “–“ берётся когда m – чётная, а “+”, когда m нечётная. При нечётном числе наблюдается max в В (светлое кольцо), при чётном в В наблюдается min (тёмное кольцо).

Если отверстие открывает только первую зону Френеля , m=1, то наблюдается в В, максимальная интенсивность, при этом A=A₁, I=A₁², наименьшая интенсивность будет наблюдаться, если открыты 2 зоны: 1 и 2.

При очень большом диаметре отверстия, и в силу того, что Am<<A₁ следовательно, соответствующая интенсивность в этом случае будет такая же, как и интенсивность при открытом всём фронте.

При освещении отверстия белым светом, кольца окрашиваются во все цвета радуги.

Дифракция на диске

закрытый диском участок волнового фронта исключают из рассмотрения, поэтому открытые зоны Френеля строят начиная от краёв диска. В этом случае суммарная амплитуда в В: А_В=А₁/2

в В наблюдается max (светлое пятно), пятно Пуассона. Этот max соответствует половине действия первой открытой зоны Френеля. Он будет окружён кольцами. Интенсивность каждого следующего кольца падает по мере удаления от центра картины. При увеличении диаметра диска, открытая зона Френеля удаляется от В, следовательно, яркость пятна Пуассона уменьшается и при очень больших размерах диска, за ним наблюдается тень вблизи границ которой наблюдается очень слабая дифракционная картина.

14. Дифракция на щели

 - угол дифракции.

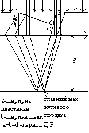
Открытую часть волновой поверхности (MN) делят на зоны Френеля, имеющие вид полос параллельных ребру M или N. Разность хода между лучами от этих зон = /2, при этом на ширине щели (a), помещается m=(asin) / (/2) зон.

Все точки волнового фронта плоскости щели колеблются в одной фазе и будут равны амплитуде вторичных волн плоскости щели, мы должны подсчитать A_B .

asin = m(/2), m-чётное = 2 4 6….

asin = 2m(/2), m=1,2,3….

Если число зон Френеля чётное то в В – min(тёмная полоса).

Если число зон нечётное: asin =  (2m+1)(/2), m=1,2,3,… то max.

Если подберём  такое, что =0, то в В будет наблюдаться центральный max., т.к. в эту точку от всех участков волнового фронта, колебания приходят в одной фазе.

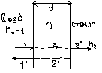
График интенсивности в зависимости от sin  (эта зависимость называется дифракционным спектром)

с уменьшением а, центральный max расширяется, при a= , в этом случае sin=1 => =90⁰, в этом случае центральный max B₀ расплывается и экран будет освещён равномерно. если a, то метод Френеля применить нельзя, т.е. размер щели должен быть значительно больше длины волны.

15. Дифракционная решётка

Д.Р.-стеклянная пластинка на которую нанесены закономерной чередующиеся прозрачные и непрозрачные промежутки.

экран находится в фокальной плоскости линзы.

AС – это разность хода между сходственными лучами от соседних щелей.

bsin = 2m(/2), min на одной щели и на решётке.

bsin = (2m+1)(/2) – max на щели.

Max Д.Р. определяется из условия интерференции лучей от соседних щелей. Если оптическая разность хода лучей от соседних щелей равна чётному числу длин полуволн, то в данной точке будет max. Если нечётное число длин полуволн, то min.

dsin = 2m(/2) (m=1,2,3,4,…) – max

dsin = (2m+1)(/2) – min

если на Д.Р. падает естественный белый свет, то в картине дифракции наблюдается дифракционный спектр.

2. Уравнения Максвелла для ЭМВ:

(,D,B,H,E – писать со знаком ветора)

(1-6)

где E и H – напряженности, D и B – индукции электрического и магнитного полей соответственно, ₀ и ₀ – соответственно электрическая и магнитная постоянные.

 - определитель Кабла или Камельтона, либо grad z.

тогда система Максвелла примет вид:

Решение этих уравнений ищем в виде:

где E₀ и B₀ – постоянные векторы, не зависящие от координат и времени:

после изменения данных формул, уравнения системы примут вид:

данная система описывает свойства и структуру плоской ЭМВ:

1)E и В перпендикулярны вектору k, поэтому данная волна является поперечной. Поперечность этих волн была открыта Юнгом в 1817 г. E,B и k – взаимно перпендикулярны.

2)из 1-го уравнения (₀₀=с²), можно получить соотношение между напряженностью электрического поля и магнитной индукцией плоской ЭМВ в вакууме: E=cB.

3) Т.к. k,_0, _0,  – вещественные величины, то это значит, что вектора E и B в плоской ЭМВ колеблются в одинаковой фазе.

Плотность потока энергии ЭМВ определяется вектором Пойнтинга: S=[ExH] (S,E,H - вектора). Направление вектора вводится в соответствии с правилом векторного произведения: S||k

плотность потока ЭМ энергии – это энергия, переносимая ЭМ волной через единичную площадку перпендикулярно вектору k.

Используя ЭМ теорию Максвелла, можно показать, что плотность импульса ЭМ волны определяется формулой : G=S/c²

Т.к. ЭМВ при своём распространении переносит импульс, то очевидно, что ЭМВ должна оказывать давление на соответствующую площадку, перпендикулярно направлению распространения => свет оказывает давление.

Давление света, падающего на плоскую поверхность перпендикулярно, в случае, когда поверхность полностью поглащает весь свет, равно:

P=Gc.

3. Законы геометрической оптики.

Закон прямолинейного распространения света - в однородной среде свет распространяется прямолинейно. Закон независимости световых пучков – пучки световых лучей, пересекаясь, не взаимодействуют друг с другом и распространяются после пересечения независимо друг от друга. Лучи – линии, вдоль которых распространяется энергия световых электромагнитных волн. Эти линии проводятся перпендикулярно волновому фронту. Световой луч можно представить как ось достаточно узкого, остающегося при этом конечной ширины светового пучка. Таким образом луч – это понятие чисто геометрическое и самостоятельного физического значения не имеет.

Законы отражения света:

1)луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одной плоскости. 2)угол падения = углу отражения (=).

Законы преломления света: 1) луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одно плоскости.2)отношение синуса угла падения  к синусу угла преломления  есть величина постоянная для данных сред: sin/sin=n. N-величина, зависящая от свойств обеих граничащих сред, называемая относительным показателем преломления второй среды относительно первой. Если свет преломляется на границе “вакуум - прозрачная среда”, то соответствующий показатель преломления называется абсолютным показателем преломления прозрачной среды. Среда с большим значением абсолютного показателя преломления называется оптически более плотной. sin/sin=n2/n1. n1sin=n2sin.

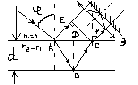
рассмотрим случай, когда лучи из оптически более плотной среды падают на границу раздела с оптически менее плотной средой.

В этом случае угол преломления , будет всё время больше угла падения . Преломленный луч при увеличении угла падения  будет приближаться к границе раздела сред (луч 1’). При некотором угле падения, называемом предельным (=пр), преломленный луч (луч 2’) скользит почти вдоль поверхности раздела сред. Угол преломления в этом случае = 90. при дальнейшем увеличении угла падения  (>пр), луч света полностью отражается от границы раздела сред (луч 3’). Это явление и называется полным отражением света.

n1sinпр=n2sin90=n2; sinпр=n2/n1; пр=arcsin(n2/n1).

В случае, когда второй средой является воздух (n2=1): пр=arcsin(1/n1)=arcsin(1/n).

1. Электромагнитные волны. Оптикой называется учение о физических явлениях, связанных с распространением и взаимодействием с веществом коротких ЭМВ, длина которых лежит в интервале [10^-4,10^-9] м. нижняя граница 10^-9 отождествляется с нижней границей прозрачности основных оптических материалов – диэлектриков. Верхний предел – условно можно отождествить с максимальной длиной волны излучения генерируемого лазером. =0.1мм – для лазера на водяных парах.

В этом диапазоне наблюдается единство всех оптических закономерностей. Основа этого единства – волновой характер ЭМВ.

шкала ЭМВ

Название

Границы диапазона

диапазона

ЭМВ

По длинам волн,

нм

min

max

- излучение

—

0,0012

рентгеновский

0,0012

12

ультрафиолетовый

12

380

видимый

380

760

инфракрасный

760

10⁶

радиодиапазон

10⁶

—

Дифференциальное уравнение ЭМВ (Максвелла)

Для вакуума, при отсутствии токов и заряда.

Уравнения Максвелла для ЭМВ:

(,D,B,H,E – писать со знаком ветора)

1-6

где E и H – напряженности, D и B – индукции электрического и магнитного полей соответственно, ₀ и ₀ – соответственно электрическая и магнитная постоянные.

Применим к обеим частям уравнения (1) операцию rot, далее воспользуемся остальными уравнениями и векторным равенством

rot rot H = rot /t D

={/x,/y,/z}

rot rot B = grad div B – ²B

[ [B] ]=( B) - ()B

div B – скалярное произведение ( B)

используя уравнения (2) и (5) мы получим:

_{- волновое уравнение для В}

-скорость света в вакууме

-волновое уравнение для Е.

Рассмотрим частный вид волнового уравнения: (3)

[! Ф=Ф(z,t)]

где функция Ф должна быть дважды дифференцируема. Решение будем искать в следующем виде: Ф(z,t)=Ф₁(z+ct)+Ф₂(z-ct). (*)

если (*) подставить в (3), то получим тождество.

Смысл этих двух решений Ф₁и Ф₂ :

функция Ф2 описывает волну произвольной формы, движущуюся со скоростью с в направлении положительных значений оси Z. В процессе движения, значения функции в каждой точке волны и форма волны не меняется. Аналогична функция Ф1 описывает волну, движущуюся в отрицательную сторону. Волна которая описывается формулой со (*), является суперпозицией двух волн, движущихся в противоположных направлениях.

В общем случае трёхмерного волнового уравнения, вводится понятие волнового вектора k, модуль которого равен волновому числу, а направление совпадает с направлением распространения волны (с осью Z). k=/c=2/ (волновое число).

В отличие от распространения в вакууме, в среде скорость ЭМВ меньше c = const и зависит от частоты. Зависимость скорости волны от частоты называется дисперсией.

Поляризация света – это физическая характеристика оптического излучения, описывающая поперечную анизотропию световых волн, т.е. неэквивалентность различных направлений в плоскости, перпендикулярной направлению распространения волны, т.е. вектору k. Если колебания E совершаются так, что его конец описывает окружность в плоскости, перпендикулярной направлению распространения волны k, то такая волна называется поляризованной по кругу.

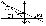
4. Явление полного внутреннего отражения.

Если свет распространяется из среды с большим показателем преломления n₁ (оптически более плотной) в среду с меньшим показателем преломления n₂ (оптически менее плотную) (n₁> n₂), например из стекла в воду, то, согласно (sin₂/sin₁)=(n₁/n₂)>1. Отсюда следует, что преломленный луч удаляется от нормали и угол преломления ₂ больше, чем угол падения ₁ (см. рис.1). С увеличением угла падения увеличивается угол преломления до тех пор, пока при некотором угле (₁= _пр) угол преломления не окажется равным /2. Угол _пр называется предельным углом. При углах падения ₁>_пр весь падающий свет полностью отражается (рис. 2).

рис.1 рис.2

По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного  растет. Если ₁ = _пр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 2). Таким образом, при углах падения в пределах от _пр до /2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Предельный угол _пр определим из формулы: n₁*sin₁ = n₂*sin₂ при подстановке в нее ₂ =/2. Тогда sin_пр = n₂/n₁ = n₂₁ . Этому уравнению удовлетворяет значениям угла _пр при n₂n₁ . Следовательно, явление полного отражения имеет место только при падении света из среды оптически более плотной в среду оптически менее плотную.

Явление полного отражения используется в призмах полного отражения (они используются в оптических приборах биноклях, перископах, а также в рефрактометрах, позволяющих определять показатели преломления тел), в световодах (светопроводах).

Если n₂₁<1, то может оказаться, что величина sin, формально вычисляемая по формуле (sin/ sin)= n₂₁, начнет превосходить единицу, т.е. sin/n₂₁>1. Соответствующего угла преломления не существует. Поэтому преломленный угол не возникает, а свет отражается полностью. Это явление называется полным отражением. Угол падения, при котором оно возникает, определяется условием ₀, причем sin₀= n₂₁. Величина ₀ называется предельным углом полного отражения.

5. Линзы. Толстые и тонкие. Рассеивающие и собирающие. Основные характеристики линз.

Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая  сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов.

Определение толстой линзы не нашел.

Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т.п. По внешней форме линзы делятся на:1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые.

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. По оптическим свойствам линзы делятся на собирающие и рассеивающие. Линзы с положительной оптической силой являются собирающими, с отрицательной  рассеивающими.

Основные характеристики: прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр О линзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линзы с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр О лежит на пересечении главной оптической оси со сферической поверхностью); главная оптическая плоскость  плоскость, походящая через оптический центр линзы перпендикулярно главной оптической оси.

6. Формула тонкой линзы, построение изображений в линзах.

Формула тонкой линзы :

(N-1)(1/R₁+1/R₂)=1/a+1/b.

N= n/n₁ относительный показатель преломления (n и n₁  соответственно абсолютные показатели преломления линзы и окружающей среды)

R₁, R₂  радиусы сфер, ограничивающих линзу.

a  расстояние от предмета до оптической плоскости линзы.

b  расстояние от изображения до оптической плоскости линзы.

Если а=, т.е. лучи падают на линзу параллельным пучком, то 1/b=(N-1)(1/R₁+1/R₂).

Соответствующее этому случаю расстояние b=OF=f называется фокусным расстоянием линзы, определяемым по формуле f=1/((N-1)(1/R₁+1/R₂)).

Если b=, т.е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком, то а=OF=f. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус  это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оси.

Величина (N-1)(1/R₁+1/R₂)=1/f=Ф называется оптической силой линзы. Ее единица  диоптрия (дптр). Диоптрия  оптическая сила линзы с фокусным расстоянием 1м: 1дптр=1/м.

Поэтому можно записать : 1/a+1/b=1/f.

Построение изображения предмета в линзах осуществляется с помощью следующих лучей: 1) луча, проходящего через оптический центр линзы и не изменяющего своего направления; 2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы; 3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси. Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным  мнимое изображение (оно прямое).

Пример построения изображения:

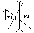Изображение отсутствует мнимое, увеличенное

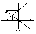
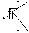
мнимое, уменьшенное, прямое

7. Принцип Гюйгенса. Когерентность и монохроматичность световых волн. Длина и время когерентности. Пространственная и временная когерентность.

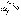При обосновании волновой теории Гюйгенс предложил принцип, позволивший наглядно интерпретировать ряд волновых задач: если в некоторый момент времени задан фронт световой волны, то для определения положения фронта через промежуток времени t надо каждую точку фронта рассматривать как вторичный источник сферической волны.

Поверхность, огибающая вторичные сферические волны радиусом сt, представляет фронт волны через промежуток времени t. Но Гюйгенс не учитывал эффекты интерференции. С учетом явления интерференции вторичных волн данный принцип носит название принципа Гюйгенса–Френеля.

Временная и пространственная когерентность. Необходимое условие существования интерференции можно сформировать в следующем виде: для возникновения интерференции необходимо, чтобы разность фаз между интерферирующими волнами сохраняла свое значение за время усреднения. Поэтому и вводят понятие когерентных колебаний, для которых разность фаз за время наблюдения остается неизменной. При описании интерференционных явлений часто используют понятия временной и пространственной когерентности. Временную когерентность обычно связывают со степенью монохроматичности волн (например, в интерферометре Майкельсона), а пространственную когерентность – с геометрией эксперимента (как в опыте Юнга).

I = I₁₀+I₂₀+2корень(I₁₀I₂₀)cos(()) – интенсивность.  - время когерентности. Под

 понимают среднее значение этих времён. =(_i)/N, _i – средние времена смены фазы колебаний. В общем случае  является характерным временным масштабом случайных флуктуаций фазы световой волны.

Путь проходимый световой волной за время  называется длиной когерентности l = c.

При рассм. пространственной когерентности необх. учитывать зависимость интерференционного слагаемого

I = I₁+I₂+корень(I₁I₂)cos() – зависимость от опт. разность хода. Эта опт. разность ходя характеризует качество волны, т.е. способность разл. участков волнового фронта к взаимной когерентности. В этом случае опт. разность хода соотв. расстоянию между соотв. точками на волновом фронте.

Оценим размеры протяжённого источника при котором интерф. картина наблюдается, т.е. когда сохр. пространственная когерентность.

2 - угловая апертура.

Максимальная разность хода достигается между лучами 1-2 или 1-3. |AD|=|BC|==bsin когда n одинаковый.

При разности хода =/2 интерференционная картина исчезает. При уменьшении значения bsin будут наблюдаться размытые интерф. полосы.

Чёткая инт. картина будет. набл., если смещение инт. картин полученных от крайних точек А и В протяжённого источника не превышает половины ширины полосы bsin/4.

Данное условие явл. условием пространственной когерентности для протяжённого источника.

8. Интерференция света. Условия, необходимые для возникновения интерференции световых волн. Разность фаз двух когерентных волн. Условия интерференционных максимумов и минимумов.

Под интерференцией света обычно понимают широкий круг явлений, в которых при наложении световых волн результирующая интенсивность не равна сумме интенсивностей отдельных волн: в одних местах она больше, в других – меньше, т.е. возникают чередующиеся светлые и темные участки – интерференционные полосы. Другими словами, интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн.

Интерференция – это перераспределение светового потока при наложении двух (или более) когерентных световых волн, в рез-те чего, в одних местах возникают максимумы, а в других минимумы интенсивности.

Под интенсивностью будем понимать I= = ½ Re(E* E) = ½ E₀², где E₀ – действительная амплитуда световой волны.

Необх. условием интерференции любых волн, явл. их когерентность, т.е. согласованное протекание во времени и пространстве двух или нескольких волновых процессов.

Строго когерентными явл. лишь монохроматические волны, т.е. волны с пост. во времени частотами, амплитудой и начальной фазой. Эти хар-ки для монохром. волн остаются постоянными бесконечно долго. Свет от реального источника не явл. монохроматическим.

Случай1. Предположим, что в некоторую точку пространства приходят две монохром. волны 1=2=, E₀₁, E₀₂, но эти волны распространяются в одном направлении и они линейно поляизованы.

E1=E₀₁exp(–i(t–1)), E2=E₀₂exp(–i(t–2)), E=E1+E2

Используя определение интенсивности:

I = I₁₀+I₂₀+2корень(I₁₀I₂₀)cos(), I1=1/2E₀₁², I2=1/2E₀₂², =2-1

Последнее слагаемое наз-ся интерференционным слагаемым.

Если колебания синфазны, т.е. 2-1 равны либо 0, либо чётно число 2, 2-1=2k, k=0,1,2...

I = I₁₀+I₂₀+2корень(I₁₀I₂₀)=(корень(I1)+корень(I2))² – максимум.

Когда в точку пространства приходят две волны в противофазе I = (корень(I1)–корень(I2))² – минимум.

Случай2. В точку пространства приходят две линейно поляризованные волны, распростр. в одном направлении, но с разными частотами и амплитудами. В этом случае последний аргумент принимает значение cos[(2-1)+(w1-w2)t].

Случай3. (для некогерентных волн). Разность фаз хаотически изменяется во времени. Это означает, что среднее значение t = 0, I=I1+I2 в любой точке пространства.

25. Соотношения неопределённостей. Их физический смысл.

В классическом представлении, в любой момент времени для каждой частицы r сказать чему равны её координаты и импульс.

Гейзенберг выдвинул гипотезу о экспериментальной невозможности измерения опред. пар связанных между собой хар-к частицы. Эта гипотеза реализовалась в виде соотн. неопред. Гейзенберга и имеет след. вид:

xp_x ħ, yp_y ħ, zp_z ħ

x  ħ/p_x, p_x должно быть равно бесконечности

p_x  ħ/x, x должно быть равно бесконечности

Это означает, что мы не можем одновременно измерить две эти хар-ки.

Физ. смысл соотношения: в природе объективно не сущ. состояний частиц, которые бы характеризовались опред. значениями, канонически сопряжённых величин x,p_x ; y,p_y

Аналогичные соотношения можно ввести для Et  ħ

E –

t – промежуток времени в теч. которого сущ. это состояние.

9. Получение когерентных пучков делением волнового фронта. Метод Юнга. Зеркала Френеля. Расчёт интерференционной картины от двух источников.

Рассм. метод деления волнового фронта. Пусть в некоторой точке пространства (1=t) E=E₀exp(-jt). В некот. точке пространства произошло разделение волны на две когерентные. В другой точке пространства М требуется получить интерференционную картину, т.е. сложить две интенсивности. Будем считать, что первая волна в пространстве прошла геом. путь S1 в среде с показателем n1, вторая – S2, n2.

E1=E₀₁cos((t–S1/V1)), E2=E₀₂cos((t–S2/V2)), V1=c/n1, V2=c/n2.

В точке М =(S2/V2–S1/V1) = (/c)(S2n2–S1n1)=(/c)(L2–L1)=2/0, L - оптическая длина пути. L=Sn, =L2–L1. 0 – длина волны в вакууме.  - разность хода оптическая.

Imax наблюдается при =x₀k=2k(₀/2), k=0,1, 2..., т.е. при чётном числе половин длин волн.

Imin наблюдается при =(2k+1)(₀/2), k=0,1, 2..., т.е. при нечётном числе половин длин волн.

Опыт Юнга.

1 путь: |S₁P|+|SS₁|

2 путь: |SS₂|+|S₂P|

=|S₂P|–|S₁P|, =корень(l²+(y+d/2)²)–корень(l ²+(y–d/2)²), d<< l, d/ l <<1

корень(l²+(y–d/2)²)=l корень(1+((yd/2)/ l)²) l(1+(yd/2)/2l²+...)

С учётом такого приближения yd/l

Разность фаз ==2/; =(2/)(yd/l)=(2dy)/(l).

В зависимости от y будет наблюдаться или max, или min.

max: /2(2k), min: /2(2k+1)

Если выведенную  подставить в формулу для суммарной интенсивности, то I(y)=I=2I₀[1+cos((2dy)/(l))].

Расстояние на экране между соседними максимумами или соседними минимумами интенсивности y=ymax0-ymax1 наз-ся шириной интерференционной полосы. y=l/d. Ширина полосы не зависит от порядка интерференции. Под порядком понимается max или min.

Зеркала Френеля.

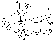т.к. точка А  как первому, так и второму зеркалу, то устанавливаем два перпендикуляра. Угол между ними равен . Луч делится на 2 луча.  очень маленький. ~1⁰ (один градус).

На участке АВ волна разд. на две части интерферирует сама с собой. Э1 – непрозрачный экран. S1 и S2 – мнимые источники. d – расстояние между источниками.

xmax = 2k l/2d, kZ, l – расстояние от источника до экрана. xmax – чётное число полуволн.

xmin = (2k+1) l/2d, kZ, l – расстояние от источника до экрана. xmin – чётное число полуволн.

b – расстояние от центра зеркал до экрана.

Зеркало 1 и зеркало 2 с точностью до очень маленького угла будут перпендикулярны прямой SS1 и делить отрезок SS1 пополам. След. S1OS равнобедренный с точностью до . OS1=OS=ra с точностью до очень маленького угла .

a=rcos, cos=1 при малом  r a

l в формулах xmax и xmin: l = r+b.

Рассм. S1S2O: d/2=rsin, sin= при малом  => d2r/

Расстоянием между двумя соседними max наз-ся расстояние между интерференционными полосами.

Расстояние между соседними min наз-ся шириной интерференционной полосы..

Ширина полосы всегда равна расстоянию между интерференционными полосами.

x=x2-x1=(k l )/d – ((k-1) l )/d=l/d – ширина полосы (расстояние между полосами), общий случай.

Ширина интерф. полосы для зеркал Френеля: x(r+b)/(2r)

Ширина луча (зона интерференции) имеет угл 2.

Т.к. зона интерф. АВ строго ограничена, то число интерф. полос конечно. N=AB/x, (AB/2/b)=tg => AB=2btg|tg (малое )|2b. N=2b/((r+b)/(2r))=2b2r/(r+b)=4rb²/(r+b)

10. Получение когерентных пучков делением амплитуды. Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона.

Происхождение интерференционной картины и способ ее получения определяет вид и зависит от способа.

Рассмотрим интерферирующее устройство, представляющее собой слой прозрачного диэлектрика с частично пропускаемыми и отражаемыми поверхностями, в котором возникает геометрическая разность хода при произвольном угле падения света на это устройство.

К такому типу интерферометров относятся плоско-параллельные и клиновидные пластины (тонкие пленки, кольца ньютона) и интерферометры, расщепляющие пучки света с помощью зеркал (интерферометр Фабри-Перо)

Различают 3 вида интерференционных полос, которые получаются при следующих условиях:

1. Полосы равного наклона, которые возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.

{ λ=const }

{ Δ=const } угол φ меняется

2. Полосы равной толщины, возникают в том случае, если интерферирующие пучки после прохождения интерферометра имеют реальное и мнимое пересечение в пространстве изображений.

λ=const}

φ=const} Δ меняется

3. Полосы равного хроматического порядка.

φ =const}

Δ =const} λ меняется

Достаточно сложные амплитудные системы, в которых требуется очень точное измерение толщины плоскопараллельной пластины или воздушных зазоров.

Рассмотрим ход луча в плоско-параллельной пластинке

Экран надо располагать в фокусе.

Пусть n1=1,n2=n;

Δ = |AE|

Δ = (AB+BC)

Δ = (AB+BC)n-AE-λ/2 – с учетом потери половины волны в точке А, так как n1=1>n2=n

Если будет выполняться противоположное условие, то потеря λ/2 будет переходить в точку B и «-λ/2» меняется на «+λ/2»

AB=BC=d/cosΘ }

AE=AC*sinφ,sinφ=n*sinΘ} Δ=2nd*cosΘ-+ λ/2

max: Δ=mλ,2k*λ/2;m=0,+-1,+-2…;k=0,+-1,+-2..

min: Δ=(2k+1)*λ/2

Если на пластинку падают не параллельные пучки света, то интерферирующие пучки будут иметь все возможные направления распространения и при заданной толщине d и заданном показателе преломления n каждому углу падения φ будет соответствовать своя интерференционная картина, поэтому такие полосы будут называться полосами равного наклона.

При оксиально симметричном распространении падающих пучков, линии равного наклона являются окружностями.

Даже если источник света протяженный и различные его точки излучают не когерентно, то интерференционная картина зависит лишь от угла падения => конечность размеров источника не смазывает картину полос равного наклона.

Полосы равной величины

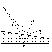
В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке C и высчитывается по той же формуле, что и для плоско-параллельной пластинки. Δ=2nd*cosΘ-+ λ/2

Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины.

Кольца Ньютона.

Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот)

В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина.

Если h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы, то r этого 2 кольца определяются так:

r²=R²-(R-h)²

считая, что h/r <<1, то h=r²/(2r)

r_m=√Rλm, m=0,+-1,+-2…

Эти концентрические окружности называются кольцами Ньютона. Интерференционная картина наблюдается как в отраженном, так и в пройденном свете. Если в отраженном свете – max, то в проходящем в данной точке – min.

Интерференционная картина может наблюдаться и в белом свете (полосы будут цветными)

Все интерференционные картины, которые рассмотрены выше, соответствую двулучевой интерференции, но можно наблюдать и многолучевую интерференцию,

11. Многослойные интерференционные покрытия. Просветленная оптика.

Интерфереционный фильтры

При определенных условиях δ=2πn пропускает без ослабления волну с определенной λ, а волны с λ немного отличающейся от той, которая пропускается, очень сильно ослабляются. Поэтому интерферометр Фабри Перо действует как узкополосный фильтр. Обычно полоса пропускания составляет порядка 10 Å, однако следует учесть, что этот фильтр пропускает не только волну с заданной λ, но и волны с λ, смещенными на целое число дисперсионных областей, то есть образующих следующие интерфереционные максимумы (в данном случае они побочные).

Чтобы убрать эффект побочного максимума надо разнести максимумы на большие расстояния. Требуется уменьшить толщину пластины (d).

Просветление оптики – должны получить высокоотражающую пластину. Это сведение к минимуму коэффициентов отражения поверхностей оптических систем, путем нанесения на них прозрачных пленок, толщина которых соизмерима с длиной волны оптического излучения.

d,n,n_c нужно подобрать так, чтобы лучи 1 и 2’ гасили друг друга, то есть их амплитуда должны быть равны и разность фаз δ=π

n=√n_c – наилучшее условие гашения

Для оценки d: условие min 2nd=(2m+1)+λ/2 => d= λ/4*((2m+1)/n), n зависит от λ, это явление называется дисперсией

Просветление оптики производят для более восприимчивой для глаз длины волны λ, которая равно 550 нм

22. Давление излучения.

Давление излучения – давление оказываемое на тела эл. магн. излучением.

Давление излучения – результат того, что фотон имеет импульс.

N – количество отраженных фотонов

(1-p)N – количество поглощенных фотонов

P = 2hpN/c + (1-p)Nh/c = Nh(1+p)/c = E_c(1+p)/c

Если ввести понятие объемной плотности энергии излучения:

W = E_c/c

P = W(1+p)

В результате взаимодействия эл. магн. излучения с поверхностью например металла под действием эл. поля волны, электроны начинают двигаться в направлении противоположном вектору ^E.

Магн поле волны падающей на метал действует на движущийся заряд силой Лоренса, кот. перпендикулярна поверхности метала, поэтому волна оказывает давление на метал.

23. Эффект Комптона.

Эффект рассеивания коротковолнового излучения (рентгеновского и гамма излучения) на свободных или слабо связанных электронах вещества, которое сопровождается увеличением длинны волны.

∆ = ^' -  = 2_c(1 - cos)

_c = h/m_ec;  - угол рассеивания

1. ^P = ^P_e + ^P’

2. W_e +  = W’_e + ’

W_e = m₀c²

 = h = hc/

’ = hc/

W’_e = sqrt(m²₀c⁴ + P²_ec²)

Эффект Комптона не может наблюдаться в видимой части спектра так – как ∆  0,1

Энергия фотона видимого света сравнима с энергией связи электрона с атомом.

24. Гипотеза Луи де Бройля.

Он постулировал универсальность корпускулярно волнового дуализма, т.е. все положения дуализма могут быть применимы ко всем частицам материи.

Это означает для каждой частицы материи можно ввести поннятия:

E = h = hc/ сл-но можнл вычислит .

Импульс P = h/ = ħk; ħ – волновое число ħ = р/2; _D = h/P = h/m₀ - длинна волны де Бройля.

Экспериментальное подтверждение гипотезы Луи де Бройля.

В эксперименте по рассеянию электронов на кристаллах и по прохождению этих частиц через вещество; если электрон рассеивается на кристалле.

По де Бройлю частица обладает волновыми свойствами сл-но с этой частицей связываем плоскую монохроматическую волну.

(^r,t)=Aexp(–I(t - kr)) – плоская монохроматическая волна.

Сделаем замену переменной в экспаненте и перейдем от  к энергии, через  = hc/ от k перейти к импульсу:

(^r,t)=Aexp(-i/ħ (Et – pr)) – плоская волна де Бройля.

12. Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. Зонные пластинки. Дифракция Фраунгофера и дифракция Френеля.

Дифракция света – совокупность явлений, наблюдаемых при распространении света сквозь малые отверстия вблизи границ непрозрачных тел и обусловленных волновой природой света.

Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. Явление дифракции имеет особенности для света: длина волны света много меньше размеров преград λ<<d. Поэтому дифракцию можно наблюдать только на достаточно больших расстояниях от преграды l>~d2/λ

Объяснить дифракцию можно используя принцип Гюйгенса – каждая точка, до которой доходит волна, служит источником вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. Принцип Гюйгенса решает задачу лишь о направлении распространения волнового фронта и волны. Решается задача чисто геометрически, поэтому из этого закона можно вывести все законы отражения и преломления света на границе 2х сред. Однако принцип Гюйгенса не решает задачу об амплитуде световой волны => об интенсивности световой волны, распространяющейся за преграду.

Вопрос: почему при распространении волны при наличии препятствия не возникает обратная волна?

Поэтому Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн.

Принцип Гюйгенса-Френеля

Световая волна, возбужденная источником S может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых фиктивными (мнимыми) источниками

При этом Френель исключил возможность возникновения обратных вторичных волн и предложил, что если между отверстием и точкой наблюдения находится экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна 0, а в отверстии – такая же, как при отсутствии этого экрана.

Закон Френеля (закон пластинки)

Согласно принципу Гюйгенса-Френеля действие источника S можно заменить действием фиктивных источников, которые расположены на вспомогательной волновой поверхности Ф. Разделим эту волновую поверхность на кольцевые зоны. Размеры этих зон таковы, что разность хода лучей от соответствующей точки Р до точки М равна λ/2:

Р1М-Р0М= λ/2, Р1М=b+ λ/2

Колебания, возбуждаемые двумя соседними зонами в точке М противоположные по фазе, так как разность хода этих 2х волн = λ/2. Поэтому при наложении этих 2х волн в точке М колебания друг друга ослабляют. Амплитуда результирующего колебания в точке М будет определяться следующим образом: Ам=А1-А2+А3-А4+…

Для оценки этих амплитуд найдем площадь зоны Френеля:

σ_m-σ_m-1=Δσ

r_m²=a²-(a-h_m)²=(b+m*λ/2)²-(b+h_m)²

h_m=(b_mλ)/2(a+b), λ<

σ_m=2πah_m= (πabλ)/(a+b)

Δσ_m= σ_m- σ_m-1=(πabλ)/(a+b)

Площадь зоны Френеля не зависит от m

Построение зон френеля: разбивают всю волновую поверхность сферической волны на равные зоны, при этом дейтвие отдельной зоны зависит от угла φm. Действие зоны тем меньше, чем больше этот угол. Действие зоны уменьшается при удалении от центральной точки Ро к периферии. Соответственно уменьшается интенсивность излучения в направлении к точке М. Означает: А1>A2>A3>… Так как общее число зон Френеля огромно, а их плошади очень малы, то можно использовать следующее приближение Am=(A_m+1+A_m-1)/2 Тогда результирующая амплитуда после подстановки в точку М от всех зон Френеля будет: Am~=A1/2 Амплитуда результирующих колебаний в точке М определяется как бы действием только половины

Если учесть h_m<<a, то r_m²=2ah_m => r_m=√(abm*(λ/(a+b)))

Если a=b=10 см, λ=500нм r1 ~= 0,158 нм

Распространение света от S к М происходит так, будто весь световой поток распределяется вдоль очень узкого канала SM , то есть свет распределяется прямолинейно. Поэтому принцип Гюйгенса-Френеля объясняет прямолинейное распространение света в однородной среде.

Если на пути монохромного света от точечного источника света поместить экран, закрывающий все зоны, кроме первой, то амплитуда в точке М будет = А, то есть увеличится в 2 раза, а интенсивность в 4 раза. Интенсивность в точке М можно увеличить с помощью зонной пластинки. В простейшем случае зонная пластинка берется прозрачная и на нее помещены по принципу зон Френеля чередующиеся прозрачные и непрозрачные кольца с радиусом r_m. Так как колебания четных и нечетных зон Френеля находятся в противофазе, они ослабляют друг друга => можно поставить данную пластинку в строго определенном месте между S и М.

Дефракция делится на дефракцию Френеля(дефракция в сходящихся лучах) и дефракцию Фраунгоффера (дефракция в параллельных лучах)

Такая классификация происходит по следующему принципу: в зависимости от расстояний от источника и от точки наблюдения до препятствия, расположенного на пути следования луча. В первом случае на препятствие падает сферическая или плоская волна, а дефракционная картина наблюдается на экране находящегося за препятствием на конечном от него расстоянии.

Во втором случае: когда на препятствие падает плоская волна, дефракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, расположенной за препятствием.

Пример для 1: дефракция на круглом отверстии, на диске

Пример для 2: дефракция на узкой щели ширины а и длины l l>>a, дефракционная решетка

19. Рассеяние света.

Рассеяние света  это процесс преобразования света в вещество, который сопровождается: 1) изменением направления распространения света; 2) появлением несобственного свечения вещества.

Мандельштам ввел понятие мутной среды  это среда, в которой взвешено множество очень мелких частиц инородных частиц. Например, аэрозоли, которые наблюдаются в облаках, дыме, тумане, различные эмульсии, коллоидные растворы.

Для таких сред показатель преломления не постоянен n(^r) (он зависит от координат пространства). Это означает, что среда оптически неоднородна.

Если введем параметр l , который характеризует неоднородность и если он l _неодн>, то свет, проходя через эту среду будет давать равномерное распределение интенсивности по всем направлениям, т.е. среда для такого света оптически однородной. Однако, если l_неодн<, то в этом случае свет рассеивается на инородных частицах этой среды и становится видимым. Этот процесс рассеивания получил название эффекта Тиндаля.

1. (^r)

2. Т(^r)

Эффект Тиндаля объяснил теоретически Рэлей и сформулировал следующий закон (закон Рэлея): интенсивность рассеянного света обратно пропорционально ⁴ : I~⁴.

20. Кванты света. Энергия, импульс фотона. Корпускулярно-волновой дуализм свойств ЭМ излучения.

К объяснению свойств света существует 2 подхода: 1) корпускулярный; 2) волновой.

1. Гипотеза Планка.

Излучение и поглощение света происходит дискретно, т.е. определенными порциями (квантами), энергия которых определяется частотой Е=h (h  постоянная Планка = 6,63*10^-34Дж*с).

2. Эйнштейн создал квантовую теорию света, согласно которой излучение и поглощение, а также распространение света происходит в виде потоков световых квантов, которые он назвал фотонами. Процесс взаимодействия света с веществом  это взаимодействие кванта (фотона) с веществом.

Фотон обладает массой m, импульс p=m*c=h/c=h/ .

3. E=m*c²  энергия фотона.

Фотоны всегда движутся в любой среде со скоростью света. Не существует в состоянии покоя, т.е. их масса покоя равна нулю.

Корпускулярно-волновой дуализм свойств ЭМ излучения. Это означает, что природу света можно рассматривать с двух сторон: с одной стороны это волна, свойства которой проявляются в закономерностях распространения света, интерференции, дифракции, поляризации. С другой стороны свет  это поток частиц, обладающие энергией, импульсом. Корпускулярные свойства света проявляются в процессах взаимодействия света с веществом (фотоэффект, эффект Комптона).

Анализируя можно понять, что чем больше длина волны , тем меньше энергия (из Е= hс/), тем меньше импульс, тем труднее обнаруживаются квантовые свойства света.

Чем меньше  => больше энергия Е фотона, тем труднее обнаруживаются волновые свойства света.

Взаимосвязь между двойственными корпускулярно-волновыми свойствами света можно объяснить, если использовать статистический подход к рассмотрению закономерностей распределения света.

Например, дифракция света на щели: при прохождении света через щель происходит перераспределение фотонов в пространстве. Так как вероятность попадания фотона в различные точки экрана неодинаковая, то возникает дифракционная картина. Освещенность экрана (количество фотонов на него падающих) пропорциональна вероятности попадания фотона в эту точку. С другой стороны освещенность экрана пропорциональна квадрату амплитуды волны I~E² . Поэтому квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотона в эту точку пространства.

21. Фотоэффект, его виды и законы. Вольт-амперная характеристика фотоэффекта. Опыты Столетова. Уравнение Эйнштейна.

Фотоэффект  это явление вырывания электронов с поверхности металла под действием электромагнитного излучения. Такой эффект называется внешним эффектом. Еще встречается внутренний фотоэффект  это вызванные электромагнитным излучением переходы электронов внутри полупроводников или диэлектриков из связанных состояний в свободные без вылета наружу.

Рис.

Впервые законы были установлены Столетовым.

Облучая катод светом, были установлены следующие закономерности: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света прямо пропорционально его интенсивности.

Томпсон измерил удельный заряд испускаемых частиц под действием света и установил, что испускаются электроны. Во всех экспериментах были сняты следующие зависимости:

Максимальное значение тока I_нас называется фототоком насыщения. Определяется таким значением напряжения, при котором все электроны достигают анода. При U=0 фототок не исчезает. Это означает, что электроны, выбитые из катода, обладают некоторой скоростью (или кинетической энергией). Для того, чтобы фототок стал равным нулю необходимо приложить задерживающее напряжение =U_зад.

Три закона Столетова (для внешнего фотоэффекта):

1. При фиксированной частоте падающего света число фотоэлектронов в единицу времени вырываемых из катода прямо пропорционально интенсивности света.

2. Для каждого вещества существует красная граница фотоэффекта, ниже которой фотоэффект не наблюдается _кр (зависит от свойств вещества).

3. Максимальная начальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от частоты падающего излучения (т.е. mv²_max/2()).

Эйнштейн вывел следующее уравнение:

h=A_вых+Е_кин , где A_вых=h_кр, Е_кин= mv²_max/2.

mv²_max/2=h- A_вых



A_внеш=eU₀

Один фотон может быть выбит только одним электроном. Возможен многофотонный нелинейный фотоэффект, при котором один электрон получает энергию у n фотонов и n может быть от 2 до 7 (наблюдается только для лазерного излучения).

16. Поляризация света. Поляризованный свет. Плоскополяризованный свет. Линейная и круговая поляризация света. Закон Брюстера.

Поляризация света – физ. характеристика оптич. излуч-я, описыв-ая попереч-ю анизотропию световых волн, т.е. неэквивалентность различных направлений в плоскости перпенд. напр-ю распр-ия волны (~k).

Световые волны, у которых напр-е колебаний векторов ~E и ~H сохр-ся неизменными в простр-ве или измен-ся по опред-му закону наз-ся поляризованными.

Если ~E световой волны клебл-ся лишь в одной неизмен-й в простр-ве пл-ти, то такая волна наз-ся линейной или плоскополяризованной. Данная пл-ть, в кот-й лежат ~E и ~k наз-ся пл-ю поляризации волны. Если колеб-я ~k соверш-ся так, что его конец описывает окружность в пл-ти перпенд-й ~k, то такая волна наз-ся поляриз-й по кругу, если эллипс – эллиптически поляризованной. Световая волна, в которой различные напр-ия ~E в пл-ти перп. ~k равновероятны, наз-ся естественной или естественно полиризованной, либо неполяризованной.

Суперпозиция 2-х линейнополяриз-х волн.

1. Волны ~E1 и ~E2 колебл-ся с одинак. частотой ω, направл. вдоль оси z, но ~E1Єxz, ~E2Єyz, Распр-ся со сдвигом фаз δ:

~E1: {E1x=E10*sin(ωt-kz); E1y=E1z=0}

~E2: {E2x=0; E2y=E20*sin(ωt-kz+δ); E2z=0}

~E=~E1+~E2={E1x+E2x;E1y+E2y:0}={Ex;Ey;0}

E2y=E20[sin(ωt-kz)cosδ+cos(ωt-kz)sinδ]

Ey=[E20/E10]Ex*cosδ+E20*sinδ*sqrt(1-(Ex/E10)²)

E_x²/E₁₀²+E_y²/E₂₀²-2[E_x/E₁₀][E_y/E₂₀]cosδ=sin²δ

Рассм. случаи:

1) cosδ=0 (δ=±π/2), sinδ=±1, E_x²/E₁₀²+E_y²/E₂₀²=1 – эллиптич. поляр. волна.

Если E₁₀=E₂₀=E₀ => E_x²+E_y²=E₀² – поляр. по кругу.

Если при наблюдении навстречу волне вращение ~E происходит по часовой стрелке, то такая волна наз-ся правополяризованной. Если против часовой – левополяризованной.

2) Если cosδ≠0 волна остается эллиптич. поляриз-й, только оси эллипса не совпадают с осями x,y и повернуты на нек-й угол. Ориентация зависит от δ.

3) cosδ=±1 (δ₊=0, δ_= π),

sinδ=0, E_x²/E₁₀²+E_y²/E₂₀²±2[E_x/E₁₀][E_y/E₂₀]=0, (E_x/E₁₀±E_y/E₂₀)²=0, E_x/E₁₀=E_y/E₂₀; Ey=[E20/E10]Ex; tgα=E20/E10

cosδ=1

cosδ=-1

Конец ~E движется вдоль прямых линий. Получаем линейнополяриз. волну с разным углом поляризации. Очевидно, что световая волна с любой поляризацией м.б. представлена в виде суперпозиции 2-х линейнополяриз-х во взаимноперпендик-х пл-х волн. Поэтому э/м волна обладает двумя независимыми состояниями поляризации.

2. Рассм. суперпоз-ю волн с левой и правой поляр-ей.

E10=E20 – круговая.

~E1: система {E1x=E0*cosωt, E1y=E0*sinωt}

~E2: система {E2x=E0*cosωt, E2y=-E0*sinωt}

~E: система {E_x=E_1x+E_2x=2E₀*cosωt, E_y=E_1y+E_2y=0}

~E – линейнополяр-я волна.

<f(t)>=(1/∆t) ₀∫^∆tfdt=(1/2)E₀²

<~E²(t)>=(1/2)E₀² – средняя интенсивность волны.

17. Распространение света в веществе. Дисперсия света. Нормальная и аномальная дисперсия света. Классическая электронная теория дисперсии света. Различия в дифракционном и призматическом спектрах.

(Обозначения: ~x – вектор над x, x* или x** - две точки над x (над вектором))

Дисперсия света – зависимость фазовой скорости света в среде от частоты. V=c/n(υ)=V(υ) – дисперсия.

На выходе: пучок разноцветных волн. Красные лучи (большая λ) преломляются слабее, т.к. для красного цвета показатель преломления меньше, чем для фиолетового. Этот спектр на экране наз-ся призматическим.

Качественная зависимость n от длины волны λ:

Такая зависимость наз-ся нормальной: dn/dλ<0 (dn/dυ>0).

Для аномальной дисперсии характерно обратное: dn/dλ>0 (dn/dυ<0).

Она наблюдается вблизи линии поглощения вещества.

Количественная характеристика дисперсии света – физ. величина D_υ=dn/dυ или D_λ=dn/dλ и наз-ся дисперсией показателя преломления.

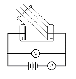
Спектры, получаемые с пом-ю призмы и с пом-ю дифр-й решетки имеют след. различия: 1. дифр. решетка разлагает свет непосред-но по λ, а призма – по значениям показателя преломления (n) (связь угла δ с …); 2. составные цвета в обоих спектрах располагаются по разному: кр. цвет дифр. решеткой отклоняется сильнее, призмой – слабее.

Классическая электронная теория дисперсии света.

c²=1/(ε₀μ₀), n(υ)=c/V, V=c/sqrt(ε), n=sqrt(ε), ε – диэлектрическая проницаемость вещества.

Дисперсия света рассматривается как результат взаимодействия э/м волны с заряженными частицами вещ-ва, кот-е совершают вынужденные колебания в переменном э/м поле волны. Электроны входящие в атом делятся на внешние (оптические) и внутренние.

Ур-е движения для оптического электрона: ~r**+γ~r*+ω₀²~r=(e/m)*~E(~r,t), ~r*≡d~r/dt, ~r(t)=A*e^-iωt. Решение: ~r(t)=((e/m)/(ω₀²-ω²-iγω))~E(t), ω₀ – собственная частота электрона внутри атома. ω – частота внешнего э/м поля.

Дипольный момент атома, индуцируемый электрическим полем э/м полем.

~p=e~r. Суммарный дипольный момент для N атомов наз-ся поляризованностью среды.

~P=N~p, N – число атомов в ед. объема/концентрация.

С др. стороны поляризованность среды или поляризация среды опред-ся формулой: ~P= ε₀χ~E – отклик среды на внешнее поле. χ – линейная диэлектрическая восприимчивость среды. При сравнении формул (указ. выше) и ф-лы вектора индукции электрич. поля (~D= ε₀~E+~P) можно легко получить связь: ε(ω)=1+χ(ω), χ(ω)=[e²N]/[mε₀(ω₀²-ω²-iγω)], ε(ω)=1+[e²N]/[mε₀(ω₀²-ω²-iγω)], n=sqrt(ε(ω)), ε(ω)=n², ε(ω)=Re(ε)+iIm(ε), n(ω)=n'(ω)+in''(ω),

Re(): (n')²-(n'')²=1+[e²N(ω₀²-ω²)]/[ε₀m((ω₀²-ω²)²+γ²ω²)], (*)

Im(): 2n'n''=[e²N(γω)]/[ε₀m((ω₀²-ω²)²+γ²ω²)] (*)

Для прозрачных или частично прозрачных в оптич. диап. диэлектриков коэф. затухания γ мал => γ²ω²<<(ω₀²-ω²)². n''≈0 => для n': (n'(ω))²=1+[e²N]/[mε₀(ω₀²-ω²)].

Легко обобщить получ-ю ф-лу для случая ансамбля оптич-х электронов с собств. частотами: (n'(ω))²=1+[e²/ε₀m]∑_i(N_i/(ω_0i²-ω²)).

Нормальная дисперсия. В дали от собственных резонансов (от ω₀) n'≈1. (n')²-1=(n'-1)(n'+1) ≈2(n'-1) => n'(ω) ≈1+[e²N]/[2mε₀(ω₀²-ω²)]

Аномальная дисперсия.

Если не пренебрегать γ, то вблизи собств. частот ω₀ n' является непрерыв. функцией, тогда из (*) выделяем мнимую и действ. часть.

n'(ω)=1+[e²N/2ε₀m]*[ (ω₀²-ω²)/((ω₀²-ω²)²+γ²ω²)], n''(ω)= [e²N/2ε₀m]*[γm/((ω₀²-ω²)²+γ²ω²)]

18. Поглощение света. Закон Бугера. Спектр поглощения. Линейчатый и молекулярный спектры. Полосы поглощения.

Поглощение света – явление уменьшения энергии световой волны при ее распространении в веществе в следствии преобразования энергии волны в другие виды.

Это явление опис-ся законом Бугера. I=I₀*e ^–kx. k – показатель поглащения зависящий от длины волны λ и от св-в вещ-ва (плотность, температура). Т.к. k зависит от λ, то данный закно м. переписать для монохр-й волны: I=I₀*e^–Kλx. k_λ зависит только от св-в вещ-ва и наз-ся спектром поглощения вещ-ва. Для одноат-х вещ-в спектр линейчатый – состоит из узких одиноч. линий.

Молекулярный спектр поглащ-я (для вещ-в сост-х из молекул) – опр-ся колеб-ми атомов в молекулах и имеет вид полос поглащения.

Коэф. поглощ-я диэлектриков: k_λ~10^-3-10^-5 1/см и у диэлектриков набл-ся селектив-е поглощ-е света в опред-х интервалах длин волн, когда k_λ резко возрастает и набл-ся сравнительно широкие полосы поглощ-я, т.е. набл-ся сплошной спектр поглощ-я. В силу отсутствия у диэл-в своб-х электр-в поглощ-е света обусл-но явл-м резонанса при вынужд-х колеб-х электр-в внутри атома и атомов внутри молекулы этого диэлектрика.

В металлах есть своб-е электроны, кот-е движ-ся под действием эл. поля световой волны => возникают быстро переменные токи => выдел-ся Джоулево тепло. Поэтому энергия св. волны быстро уменьш-ся, превращаясь во внутр. эн. металла. Чем больше провод-ть мет., тем сильнее поглощ-ся свет => металлы для света непрозрачны. k_λ~10⁴ 1/см.