Полевой эффект и его применение


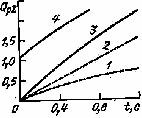
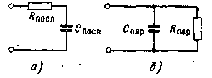
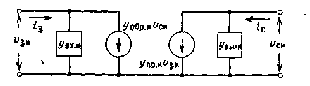
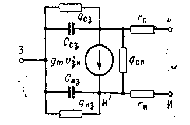
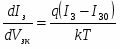
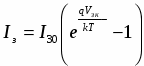
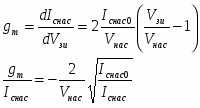
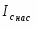
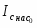
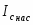
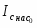
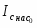
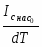
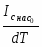
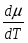
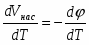
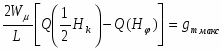
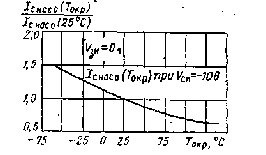
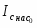



 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
Ульяновский государственный педагогический университет имени И.Н. Ульянова
Кафедра общей физики
Курсовая работа
Полевой эффект и его применение
.
Ульяновск
2010
Содержание
В настоящее время большое внимание уделяется изучению эффекта поля. На основе эффекта поля создан целый класс полупроводниковых приборов, таких как полевые транзисторы, репрограмируемые элементы памяти с плавающим затвором, приборы с зарядовой связью (ПЗС) и т. п.
В 1958-1959 годах появились первые интегральные микросхемы на кремнии, что означало появление нового научного направления полупроводниковой электроники – микроэлектроники. При этом удалось существенно уменьшить стоимость и повысить надежность устройств электронной техники, значительно уменьшить их массу и габариты путем формирования всех пассивных и активных элементов интегральных микросхем в едином технологическом процессе, также в результате конструктивной интеграции.
Первое практическое применение, полевого эффекта было осуществлено в 1960 г. Несколькими десятилетиями раньше уже были заложены основы работы полевых транзисторов, но для их окончательной разработки потребовались многолетние исследования. В 1970 г были созданы первые приборы с зарядовой связью. В 1975 г ПЗС начали активно внедряться в качестве телевизионных светоприёмников. [7,13]
Конструктивное интегрирование функций фоточувствительных и сканирующих элементов в одном приборе позволяет считать ПЗС наиболее перспективными для создания полностью твердотельной ФСИ.
Полупроводниковые приборы принцип действия, которых основан на эффекте поля, имеют множество достоинств, таких как надежность, достаточно малые геометрические размеры, низкий уровень шумов, быстродействие и т.п. Дальнейшее совершенствование приборов привело к ряду проблем, решение которых является главной задачей полупроводниковой электроники. Среди проблем наиболее значимыми являются, например, ограничение рабочих частот, ограничение быстродействия и т.д.[7]
Целью курсовой работы:
Изучение принципа действия полевых приборов и исследование их характеристик.
Задачи курсовой работы:
Изучение эффекта поля в полупроводниках.
Изучение принципа работы полупроводниковых полевых транзисторов.
Экспериментально исследовать:
Исследование статические характеристики полевых транзисторов.
Исследовать зависимость статических характеристик полевых транзисторов от температуры.
В данной работе в первой главе рассматривается частотная зависимость полевого эффекта и наиболее актуальные на сегодняшний день вопросы о применении этого явления в оптоэлектронике. Во второй главе рассматриваются физические основы полевого эффекта. В третьей главе ― применение изучаемого явления на примере принципа действия полевых транзисторов и приборов с зарядовой связью. В четвёртой главе рассматриваются основные характеристики полевых транзисторов. Пятая Глава раскрывает физические основы работы и конструкции приборов с зарядовой связью. Шестая глава посвящена экспериментальному изучению основных параметров полевого транзистора, а также изучение частотной зависимости параметров полевого транзистора КП303Г.
1.1 Эффект поля в германии при высоких частотах
Изменение проводимости приповерхностного слоя полупроводника, вызываемое электрическим полем, перпендикулярным этой поверхности, обычно называют эффектом поля. Исследование эффекта поля в германии при высоких частотах приводит к некоторым трудностям, так как возникают большие токи смещения, идущие к поверхностной области. [8]
Эффективная подвижность носителей тока, индуцированных у поверхности полупроводника при приложении поля, часто гораздо меньше подвижности носителей в объеме образца; причина заключается в том, что часть носителей связана на поверхностных уровнях. При достаточно высоких частотах поверхностные уровни не смогут успевать обмениваться с зоной проводимости или валентной зоной и эффективная подвижность в таком случае будет равна объемной подвижности основных носителей.
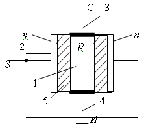
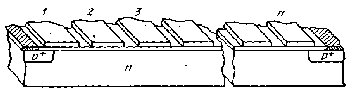
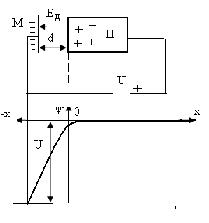
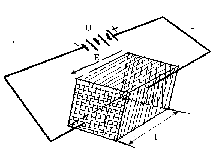
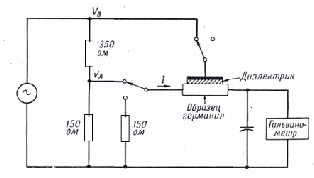
Рисунок 1. Схема установки для эффекта поля.
Данное исследование проводилось на экспериментальной установке показанной на рисунке 1.
Образец представлял собой прямоугольный параллелепипед размерами 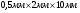 , вырезанный из монокристалла германия; к концам образца были припаяны контакты. Поверхность образца подвергалась различным видам обработки.
, вырезанный из монокристалла германия; к концам образца были припаяны контакты. Поверхность образца подвергалась различным видам обработки.
Образец германия являлся одной из пластин конденсатора, а диэлектриком служила пластина из монокристалла титаната стронция, при этом емкость системы составляла ~ 30 пФ. Конденсатору было приложено переменное напряжение в 10В, создающее максимальное поле порядка 4 104 В /см. Между концами образца германия было приложено меньшее напряжение той же частоты и фазы. В результате модуляции этого напряжения при изменениях проводимости, вызываемых эффектом поля, в цепи гальванометра индуцируется постоянный ток, который, пропорционален эффекту поля.
Эффект поля можно охарактеризовать эффективной подвижностью носителей тока
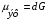 1
1 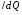 (1)
(1)
где 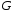 1- проводимость образца на единицу поверхности, а
1- проводимость образца на единицу поверхности, а 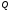 - полный заряд, индуцированный полем на единице поверхности. Полная проводимость равна
- полный заряд, индуцированный полем на единице поверхности. Полная проводимость равна
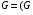 1
1 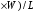
где W- ширина, а L - длина образца, тогда
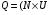 В
В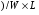

здесь С-полная емкость между пластиной и образцом, 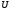 В-напряжение приложенное к емкости. Отсюда следует
В-напряжение приложенное к емкости. Отсюда следует
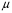 эф
эф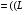 2
2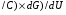 В (2)
В (2)
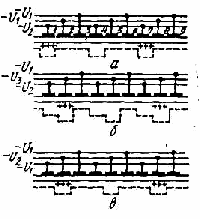
Приложенные напряжения, показанные на рисунке 1, синусоидальны со среднеквадратичными значениями VA и VB и могут быть записаны в виде
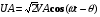 (5а)
(5а)
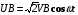 (5б)
(5б)
где 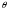 - фазовый сдвиг между приложенными напряжениями. При малых изменениях проводимость может быть записана следующим образом:
- фазовый сдвиг между приложенными напряжениями. При малых изменениях проводимость может быть записана следующим образом:
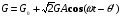 (3в)
(3в)
где θ'- фазовый сдвиг электропроводности по отношению к 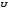 В.Ток вдоль образца при напряжении
В.Ток вдоль образца при напряжении 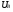 будет
будет
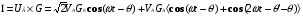 (4)
(4)
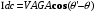 (5)
(5)
Обычным приемом теории переменного тока можно расширить простое определение (1) 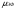 , представляя
, представляя 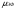 как комплексное число, модуль которого равен отношению амплитуд двух синусоидальных величин
как комплексное число, модуль которого равен отношению амплитуд двух синусоидальных величин 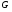 1и
1и 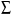 , а аргумент равен фазовому сдвигу между двумя синусоидами. Из уравнения (2) следует, что величина
, а аргумент равен фазовому сдвигу между двумя синусоидами. Из уравнения (2) следует, что величина 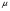 эф
эф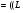 2
2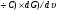 В, а из уравнения (3) видно, что равна θ'. Из изложенного и уравнения (5) следует
В, а из уравнения (3) видно, что равна θ'. Из изложенного и уравнения (5) следует
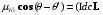 2)
2)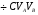 (6)
(6)
Это основное соотношение между 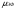 и экспериментальными величинами.
и экспериментальными величинами.
В случае использование схемы, показанной на рисунке 1 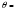 0, когда
0, когда 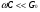 (т.е. ниже нескольких МГц в этих опытах). Для этого диапазона частот из уравнения (6) видно, что измерения дают
(т.е. ниже нескольких МГц в этих опытах). Для этого диапазона частот из уравнения (6) видно, что измерения дают 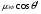 , т.е. действительную часть
, т.е. действительную часть 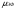 . На практике верхняя часть частот определяется условием
. На практике верхняя часть частот определяется условием 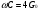 . Вблизи этой частоты ток смещения через емкость, индуцируемый напряжением
. Вблизи этой частоты ток смещения через емкость, индуцируемый напряжением 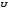 В, сравним с продольным током от напряжения
В, сравним с продольным током от напряжения 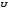 А (ток и напряжение изменяются вдоль образца), и величиной
А (ток и напряжение изменяются вдоль образца), и величиной 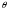 ни в коем случае нельзя пренебречь. В этой области частот единственным способом оценки
ни в коем случае нельзя пренебречь. В этой области частот единственным способом оценки 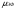 является расчет распределения тока и напряжения с последующим интегрированием их произведения вдоль образца. Выше этой области частот такие расчеты становятся не реальными, потому что они критически зависят от симметрии распределения токов, которое трудно в этом случае определить.
является расчет распределения тока и напряжения с последующим интегрированием их произведения вдоль образца. Выше этой области частот такие расчеты становятся не реальными, потому что они критически зависят от симметрии распределения токов, которое трудно в этом случае определить.
Для достижения диапазона высоких частот, поле ограничивалось участком образца около центра, а последовательно с пластиной был помещен небольшой конденсатор. Обе эти меры уменьшили отклонения гальванометра, но зато увеличили верхнюю границу частот
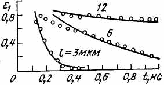
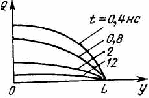
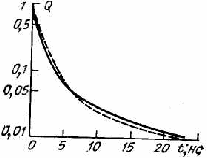
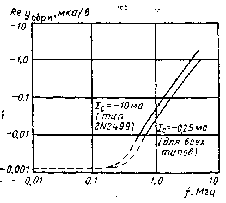
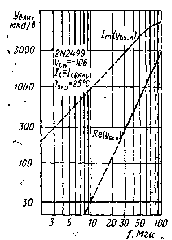
Таким образом, была рассмотрена зависимость эффективной подвижности в германии p-типа в расширенной области частот (рисунок 2).[8,10]
Перед снятием зависимости поверхности образца были протравлены в течение 1 мин в СР-4,
Измерения проводились в сухом кислороде, влажном воздухе, а так же в озоне.
В сухом кислороде наблюдалось уменьшение времени жизни, а также уменьшение эффективной подвижности. Следует отметить тот факт, что независимо от среды, и не зависимо от числа повторяемых циклов, наблюдались лишь незначительные изменения эффекта поля.
Рисунок 2.Эффективная подвижность в германии p –типа в расширенной области частот.
В результате различного вида обработок, наблюдалось разрушение инверсионного слоя, что приводило к уменьшению эффекта поля.
При частотах порядка нескольких сотен Герц между быстрыми поверхностными состояниями, зоной проводимости и валентной зоной устанавливается равновесие. При частотах в области сотен килогерц наблюдается квазиравновесие между быстрыми поверхностными состояниями и ближайшей зоной. С некоторыми оговорками, касающимися надежности данных при частотах выше 10 МГц, можно по крайне мере предполагать, что время, требуемое для установления квазиравновесия между быстрыми состояниями и одной из зон, порядка 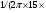 106)= 10-8 сек.
106)= 10-8 сек.
На сегодняшний день актуальным является нахождение методов расширения диапазона частот [8].
Полевой транзистор (ПТ) был изобретен за много лет до классических работ Бардина, Браттэна, Пирсона и Шокли конца 40-х годов, приведших к созданию точечного и биполярного транзисторов. Еще в 1925 и 1926 гг. Дж. Е. Лилиенфельд подал заявки в патентные бюро Канады и США, озаглавленные «Метод и прибор управления электрическими токами» [1], в которых он предложил полупроводниковый прибор с управляющим электродом. В 1935 г., независимо от Лилиенфельда, О. Хейл [2] описал тонкопленочный полевой прибор с одним и двумя затворами. Серьезные исследования в этом направлении не были осуществлены в то время из-за недостаточного уровня развития физики поверхности полупроводников.
Работы, выполненные в лабораториях «Бэлл Телефон» в конце 40-х годов, были первоначально направлены на создание полевого прибора. Однако результаты, полученные Шокли и Пирсоном [3] в 1948 г., разочаровали исследователей. В экспериментах использовались тонкие германиевые пленки, изолированные от управляющего электрода (затвора) тонкой пленкой слюды. Изменение проводимости германия в функции потенциала затвора регистрировалось с помощью двух электродов, присоединенных к образцу. Наблюдавшаяся модуляция проводимости была значительно меньше ожидаемой, поскольку большая часть («90%) индуцированного заряда захватывалась поверхностными состояниями. В результате этих экспериментов, а также вследствие изобретения точечных и биполярных транзисторов интерес к исследованию приборов с полевым управлением несколько угас, однако проведенная работа явилась большим вкладом в развитие физики поверхностных явлений.
В 1952 г. Шокли [4] дал теоретическое описание активного прибора нового типа, названного им униполярным полевым транзистором. Принцип действия его, в отличие от биполярного транзистора, основан на модуляции тока основных носителей.
Модуляция тока осуществлялась изменением толщины проводящего канала путем расширения или сужения обедненной области р-n-перехода. Вредное действие поверхностных ловушек было исключено тем, что проводящий канал располагался достаточно далеко от поверхности полупроводника.
Основным преимуществом этого прибора являлось высокое входное сопротивление за счет включения управляющего р-n перехода в запорном направлении. Однако трудности изготовления униполярного транзистора при существовавшем уровне техники были весьма значительными,- и несмотря на то, что вскоре после опубликования работы Шокли были описаны приборы, изготовленные на кремнии и германии, широкого практического применения они не нашли. Ситуация изменилась с появлением технологии маскирования, диффузии и эпитаксиального наращивания, позволившей изготовлять качественные полевые приборы с хорошей воспроизводимостью параметров.
Интерес к полевым транзисторам с изолированным затвором оживился после успешных экспериментов Аталлы и др. [5] по пассивации поверхности кремния наращиванием слоя окисла. В этих опытах была получена достаточно низкая плотность поверхностных состояний, ответственных за захват заряда, наведенного управляющим электродом. В 1960 г. Канг и Аталла [6] предложили использовать структуру металл — окисел — полупроводник (МОП), в которой металлический электрод управлял проводимостью между двумя обратно смещенными диодами, расположенными на поверхности полупроводника. Этот прибор, названный МОП-транзистором, в дальнейшем был усовершенствован Хофштейном и Хайманом [7], которые описали транзисторы, работающие в режиме обогащения или обеднения, в зависимости от напряжения, на затворе. Большой вклад в развитие теории полевого транзистора был сделан Иантоллой, Моллом и Са [8, 9].
Параллельно с этими разработками велись исследования другой разновидности полевых приборов, использующих тонкие поликристаллические полупроводниковые пленки. Первый пленочный полевой транзистор (ППТ) был разработан Ваймером с сотрудниками [10] в лаборатории фирмы «Рэдио корпорейшн оф Америка». Впоследствии было исследовано достаточно большое количество структур с применением различных полупроводниковых материалов, однако проблемы захвата заряда и стабильности параметров для них еще полностью не разрешены. Вследствие этого тонкопленочные транзисторы не используются так широко, как приборы с МОП-структурой.
1.3 Полевой транзистор с управляющим р—n-переходом (ПТУП)
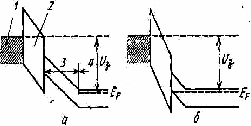
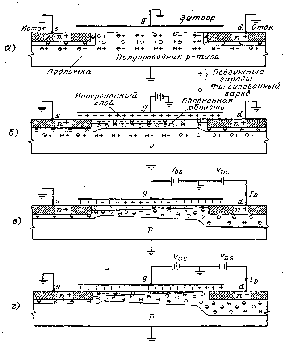
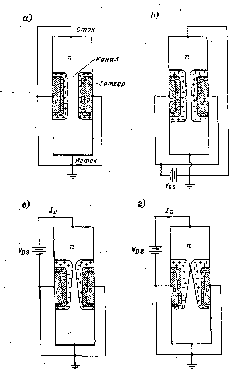
Схематическое изображение ПТ с управляющим р-n переходом (униполярный транзистор Шокли) приведено на рис. 3 .
Прибор состоит из области с проводимостью n- (или р-) типа, имеющей омические контакты, называемые истоком и стоком, и двух областей р- (или n-) типа, называемых затворами .
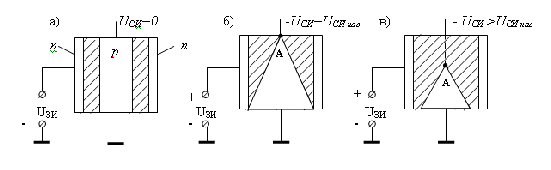
На рис. 3, а показан случай нулевого напряжения на всех электродах. За счет наличия обедненных областей вблизи р-n переходов толщина проводящего канала между истоком и стоком меньше геометрического сечения n-области. Если к затворам приложить обратное смещение VGS, to размеры областей пространственного заряда (ОПЗ) увеличиваются и толщина проводящего канала еще более уменьшается (рис. 3, б).
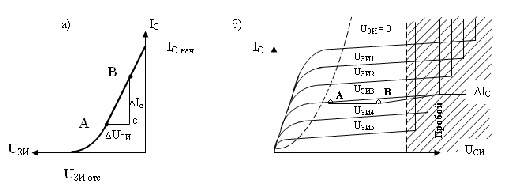
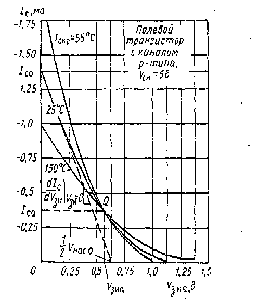
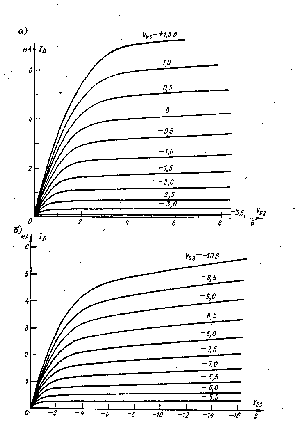
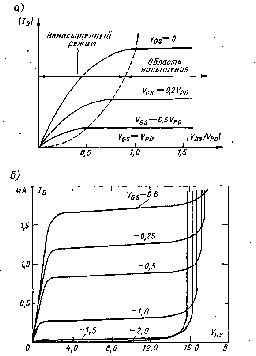
При приложении к стоку положительного по отношению к истоку напряжения VDS по каналу течет ток ID основных носителей (электронов), а толщина ОПЗ у стокового конца затвора увеличивается вследствие возрастания обратного напряжения между затвором и каналом (рис. 3, в). Таким образом, возрастание VDS приводит к увеличению сопротивления канала за счет уменьшения «горловины» вблизи стока. При достаточно больших значениях VDS области пространственного заряда смыкаются (рис. 3, г) и дальнейшее увеличение VDS практически не вызывает возрастания тока (режим насыщения). Напряжение между затвором и стоком, соответствующее смыканию ОПЗ, называется напряжением перекрытия Vp0. Следует отметить, что канал может быть полностью перекрыт только при ID=0. При работе прибора в режиме насыщения вблизи стока существует очень узкая проводящая область, в которой плотность тока и электрическое поле велики. На стоковых характеристиках ПТУП (рис. 4, а) точки сечения штриховой линии с кривыми ID (VDS/VPO) соответствуют началу режима насыщения.
На практике при насыщении все же наблюдается незначительное возрастание тока с ростом VDS (рис. 4,б), причины которого полностью не ясны. По-видимому, это возрастание связано с распространением ОПЗ по направлению к стоковому контакту и частично с увеличением электрического поля в канале. За счет расширения области смыкания в сторону истока ток стока возрастает так, как если бы длина затворов уменьшалась, а толщина канала оставалась постоянной. Это явление, называемое эффектом укорочения канала, определяет конечную величину сопротивления канала при увеличении VDS.
Рассмотрим влияние напряжения затвора на характеристики прибора. Пусть 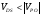 , a VGS = 0. Этот случай соответствует ненасыщенному режиму работы (рис. 2,а). При увеличении обратного смещения на затворе толщина канала уменьшается, ток стока падает, и при
, a VGS = 0. Этот случай соответствует ненасыщенному режиму работы (рис. 2,а). При увеличении обратного смещения на затворе толщина канала уменьшается, ток стока падает, и при 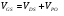 , где
, где 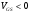 и
и 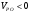 , наступает режим насыщения. Таким образом, с ростом
, наступает режим насыщения. Таким образом, с ростом 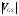 значение VDS, соответствующее началу насыщения, уменьшается. С дальнейшим возрастанием |VGS| ток стока становится равным нулю при VGS=VPO. При этом канал полностью перекрыт и представляет собой сплошную обедненную область.
значение VDS, соответствующее началу насыщения, уменьшается. С дальнейшим возрастанием |VGS| ток стока становится равным нулю при VGS=VPO. При этом канал полностью перекрыт и представляет собой сплошную обедненную область.
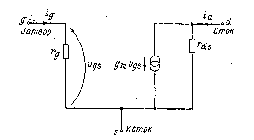
Низкочастотная эквивалентная схема ПТУП для малых сигналов приведена на рис. 5 [4], где rg и rds — дифференциальные сопротивления затвора и стока соответственно,
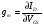 — крутизна передаточной характеристики.
— крутизна передаточной характеристики.
Для типичных маломощных кремниевых приборов в режиме насыщения 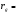 109 Ом,
109 Ом, 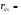 30 кОм,
30 кОм, 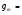 2 мА/В. Путем увеличения рабочей площади транзистора крутизна может быть повышена до 100 мА/В, а допустимая мощность рассеяния до 10 и более ватт; однако при этом величины rg и rds уменьшаются, а входная емкость возрастает.
2 мА/В. Путем увеличения рабочей площади транзистора крутизна может быть повышена до 100 мА/В, а допустимая мощность рассеяния до 10 и более ватт; однако при этом величины rg и rds уменьшаются, а входная емкость возрастает.
Стоковые характеристики ПТУП с достаточной степенью точности могут быть аппроксимированы выражением [17]:
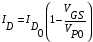 (7)
(7)
где IDO — ток стока при VGS = 0; n — константа, лежащая в пределах 1,5—2,5; штрихом здесь и далее обозначаются величины параметров для режима насыщения.
Дифференцирование (7) дает выражение для крутизны передаточной характеристики:
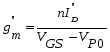 (8)
(8)
Максимальная крутизна, которую можно получить, не смещая управляющий переход в прямом направлении, будет соответствовать VGS = 0. Обозначая это значение крутизны через gmo, из (8) получаем
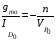 (9)
(9)
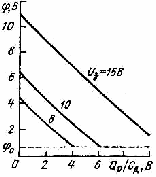
Поскольку n2, а минимальная величина VP0, получаемая на практике «1В, то максимально достижимое значение gmo/IDO составляет 2 В-1. Отношение gmo/IDO является удобным параметром, характеризующим качество работы прибора на низких частотах.
Преимуществами ПТУП по сравнению с биполярными транзисторами являются не только его высокое входное сопротивление, но и более низкий коэффициент шума, а также возможность подбора смещения, обеспечивающего нулевой температурный коэффициент тока стока.
Важными параметрами ПТУП являются его высокочастотные и переключающие свойства. Поскольку ПТУП представляет собой прибор, работающий на основных носителях, для него отсутствуют эффекты накопления заряда, свойственные биполярным транзисторам.
При рассмотрении высокочастотных свойств ПТУП его удобно представить как прибор, управляемый зарядом, так как для изменения тока стока необходимо изменить полный заряд в обедненной области канала. Скорость изменения этого заряда зависит от постоянной времени, определяемой величиной барьерной емкости затвор — канал и сопротивлением канала, которое достаточно велико. Эта постоянная времени и ограничивает возможности работы прибора на высоких частотах.
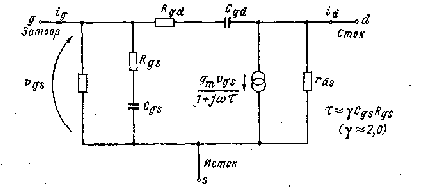
Точная эквивалентная схема областей затвора и канала представляет собой распределенную RC-цепь [18]. Для упрощения ее часто заменяют приближенной моделью, представленной на рис. 6 [19], где Cgd + Cgs — полная емкость затвор-канал, a Rgd и Rgs— составляющие сопротивления канала.
В режиме насыщения и в отсутствие эффекта укорочения канала Cgd0, a Rgd В реальном же случае емкость Cgd остается отличной от нуля, хотя и значительно меньшей, чем в ненасыщенном режиме. Если в цепи стока включено нагрузочное сопротивление, эквивалентная входная емкость может сильно возрасти за счет эффекта Миллера аналогично увеличению проходной емкости лампового триода.
1.4 Транзисторы со структурой металл-диэлектрик-полупроводник (МДП)
Рис. 7. Принцип действия МДП-транзистора" инверсионного типа
МДП-транзистор представляет собой полевой прибор, в котором металлический затвор изолирован от полупроводника тонким слоем диэлектрика. Пленочные полевые транзисторы (ППТ обычно относят к другому классу, поскольку в отличие от МДП-приборов они выполняются на изолирующей подложке. Кроме того, ППТ имеют значительно меньшую толщину активной области полупроводника.
МДП-транзисторы могут быть классифицированы по способу создания проводящего канала. В большинстве приборов используется проводящий инверсионный слой вблизи границы диэлектрик — полупроводник. Существуют, однако, приборы, называемые транзисторами с глубоким обеднением [20,21], основанные на эффекте. уменьшения проводимости канала, расположенного на некотором удалении от поверхности полупроводника. Подвижные носители в инверсионных ППТ- и МДП-транзисторах находятся в приповерхностной области полупроводника, а их концентрация зависит от электрического поля, создаваемого затвором. Это существенно отличает ППТ- и МДП-приборы от рассмотренных выше транзисторов с управляющим р-n-переходом.
Принцип работы МОП-транзистора инверсионного типа проиллюстрирован рис. 7. Для простоты полагается, что затвор отделен от полупроводника идеальным изолятором, а влияние поверхностных ловушек не учитывается. Распределение зарядов при нулевых напряжениях на электродах показано на рис. 5, а. Вблизи n+-областей, созданных диффузией для образования истока и стока, имеются области пространственного заряда, возникшие за счет внутренней разности потенциалов на n+-р переходах. Поскольку в р-области электроны практически отсутствуют, сопротивление-исток — сток весьма велико и соответствует сопротивлению двух встречно включенных диодов при нулевом смещении.
Если к затвору приложено положительное напряжение (рис. 7,б), вблизи поверхности происходит инверсия типа проводимости, так что в этой области концентрация электронов становится достаточно высокой и сопротивление сток - исток резко уменьшается.
При подаче положительного напряжения на сток (рис. 7, в) электроны начинают двигаться от истока к стоку по инверсионному слою. За счет падения напряжения вдоль канала нормальная составляющая поля затвора и соответственно концентрация электронов уменьшаются в направлении от истока к стоку. Толщина же обедненной области под инверсионным слоем в этом направлении увеличивается вследствие возрастания разности потенциалов между подложкой и каналом.
Когда напряжение на стоке превысит определенную величину (рис. 7,г), происходит перекрытие канала вблизи стока, и ток через прибор выходит на насыщение так же, как и в транзисторе с управляющим р-n-переходом. Эффекты укорочения канала и электростатической обратной связи, приводящие к тому, что дифференциальное сопротивление стока на практике остается конечным, будут рассмотрены в гл. 7.
Для приборов, в которых диэлектриком является окисный слой (МОП-транзисторы), существенную роль играет положительный заряд, присутствующий в окисле. Действие этого заряда эквивалентно наличию положительного напряжения на затворе, так что в случае полупроводника р-типа инверсионный слой существует уже при нулевом управляющем напряжении. Для n-полупроводника присутствие положительного пространственного заряда в окисле вызывает образование слоя с повышенной концентрацией электронов (n+), поэтому для создания инверсионного слоя напряжение на затворе должно превышать некоторую пороговую величину, достаточную для нейтрализации этого заряда. Таким образом, проводимость канала МОП-транзистора на подложке р-типа (n-канал) можно увеличивать или уменьшать в зависимости от полярности напряжения на затворе. В случае же подложки n-типа (р-канал) при VGS=0 канал отсутствует и для его создания необходимо приложить VGS<0, т. е. такие приборы могут работать только в режиме обогащения канала неосновными носителями (дырками). МОП-транзисторы с n-каналом принято называть транзисторами с обеднением, несмотря на то, что они могут работать также и в режиме обогащения канала неосновными носителями (электронами). Типичные стоковые характеристики обоих типов МОП-транзисторов приведены на рис. 8.
Выше предполагалось, что подложка легирована относительно слабо. О возрастанием степени легирования для образования инверсионного слоя необходимо прикладывать большее напряжение к затвору. Увеличивая концентрацию легирующей примеси в приборах на подложке р-типа, можно нейтрализовать действие положительного заряда в окисле и получить МОП-транзистор с индуцированным n-каналом.
Напряжение на затворе, при котором ток стока уменьшается до нуля, называется пороговым напряжением W, причем VT<0 для транзисторов как с р-, так и с n-каналом (см. рис. 8).
Минимальное напряжение сток — исток, необходимое для достижения насыщения, как и в случае ПТУП,
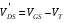 .
.
Приближенное выражение для тока стока в области до насыщения легко может быть получено при следующих упрощающих предположениях [9, 22]:
а) влияние поверхностных ловушек и контактные разности потенциалов не учитываются;
б) в диэлектрике присутствует фиксированный заряд с поверхностной плотностью Qss;
в) данный заряд на затворе наводит равный по величине и противоположный по знаку подвижный заряд вблизи поверхности полупроводника;
г) эффективная подвижность носителей в канале считается не зависящей от электрического поля в полупроводнике.
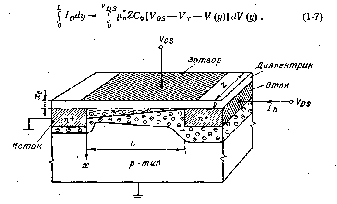
Для прибора, изображенного на рис. 9, ток ID, протекающий по каналу, создает падение напряжения V(y) по отношению к истоку, так что на расстоянии у от истока напряжение между затвором и каналом будет 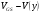 . Тогда заряд, наводимый в полупроводнике на элементе площади Zdy, будет
. Тогда заряд, наводимый в полупроводнике на элементе площади Zdy, будет
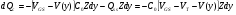 (1.4),
(1.4),
где 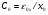 — удельная емкость диэлектрика; x0 — его толщина;
— удельная емкость диэлектрика; x0 — его толщина; 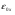 — диэлектрическая проницаемость окисла;
— диэлектрическая проницаемость окисла; 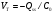 — пороговое напряжение.
— пороговое напряжение.
Если весь наведенный заряд подвижен, то
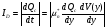 , (10)
, (10)
где 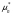 — эффективная подвижность электронов в инверсионном слое.
— эффективная подвижность электронов в инверсионном слое.
Подставляя (25) в (10), находим
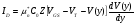 (11)
(11)
Интегрируя (11) по y и учитывая, что V(L)=VDS, V(0) = 0, получаем
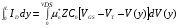 (12)
(12)
Рис. 9. Схематическое изображение n-канального МДП-транзистора
Так как ID не зависит от у, то из (12) следует:
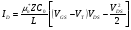 (13)
(13)
Выражение (13) справедливо при условии
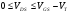 (n-канал);
(n-канал);
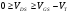 (р-канал).
(р-канал).
При 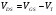 происходит перекрытие канала, при этом ток стока согласно (1-8) достигает наибольшего значения
происходит перекрытие канала, при этом ток стока согласно (1-8) достигает наибольшего значения 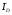 .
.
Будем считать, что ток стока в области насыщения остается постоянным и равным 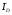 . Тогда из (1.8) следует, что передаточная характеристика в области насыщения имеет квадратичную форму:
. Тогда из (1.8) следует, что передаточная характеристика в области насыщения имеет квадратичную форму:
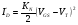 (14),
(14),
где 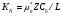
Величина KN является удобным коэффициентом для оценки качества работы прибора на низких частотах.
Крутизна передаточной характеристики при насыщении, как следует из (14), линейно зависит от VGS:
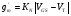 (15)
(15)
Используя (14) и (15), KN можно выразить через 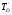 и
и 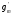 :
:
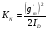 (16)
(16)
Для промышленных приборов эти параметры легко могут быть измерены или оценены из паспортных данных.
Экспериментально найдено, что для большинства МОП-приборов сопротивление сток — исток в режиме насыщения обратно пропорционально току стока. Поэтому максимальный коэффициент усиления по напряжению 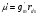 с помощью (16) может быть представлен в виде
с помощью (16) может быть представлен в виде 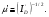 Таким образом, для получения большого усиления по напряжению необходимо уменьшать ток стока.
Таким образом, для получения большого усиления по напряжению необходимо уменьшать ток стока.
Эквивалентная схема МОП-транзистора на низких частотах имеет такой же вид, как и для ПТУП (рис. 5). Ток утечки затвора типичного МОП-прибора составляет 10-15 А, т. е. на несколько порядков меньше тока затвора ПТУП. В специальных конструкциях МОП-ПТ с охранными кольцами ток утечки затвора может быть уменьшен до 10-17 А, что делает такие транзисторы идеальными приборами для электрометрических измерений.
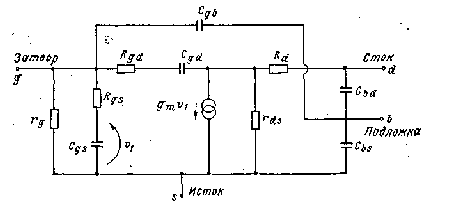
Упрощенная высокочастотная эквивалентная схема МОП-ПТ (рис. 10) отличается от соответствующей схемы ПТУП (рис. 6) добавлением емкостей Сbd и Cbs n+-р-переходов подложка сток и подложка — исток и последовательного сопротивления Rd- Кроме того, в схему включен конденсатор Cgb, учитывающий емкость вывода затвора и емкость, обусловленную влиянием напряжения затвора на заряд обедненной области подложки. В режиме инверсии Cgb обычно мала, однако при запертом транзисторе ее величина может составлять значительную часть общей входной емкости.
Сопротивление Rd может иметь заметную величину для приборов со встроенным каналом. В таких транзисторах для уменьшения емкости затвор—сток, затвор размещается так, чтобы он не перекрывался со стоком. Вследствие этого проводимость небольшой части канала вблизи стока не модулируется напряжением на затворе, что приводит к появлению последовательного сопротивления стока порядка нескольких сотен Ом. Очевидно, что в приборах с индуцированным каналом затвор должен перекрываться с истоком и стоком, так как немодулируемая часть канала представляла бы собой разрыв цепи.
В заключение данного раздела отметим некоторые особенности схемных применений разных типов МОП-транзисторов.
Поскольку в приборах со встроенным каналом длина затвора обычно меньше расстояния сток—исток, они обладают лучшими высокочастотными свойствами из-за меньшей величины входной емкости. Другое достоинство транзисторов этого типа — возможность получения равенства потенциалов входа и выхода в схеме истокового повторителя.
Существенным преимуществом приборов с индуцированным каналом является простота построения на их основе усилителей напряжения, а также логических и запоминающих схем с гальваническими связями.
Рис. 10. Упрощенная высокочастотная эквивалентная схема МОП-ПТ
1.5 Пленочные полевые транзисторы (ППТ)
Тонкопленочные транзисторы, в отличие от МДП-ПТ, создаются на диэлектрической подложке. Это существенно упрощает проблему изоляции большого количества элементов при конструировании интегральных схем.
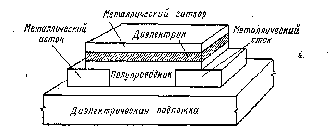
На рис. 11 приведено схематическое изображение ППТ, полученного последовательным напылением в вакууме слоев металла, полупроводника и диэлектрика [23]. Полупроводниковая пленка, как правило, является поликристаллической с большой концентрацией ловушек на границах раздела с диэлектриком. Величина порогового напряжения, по-видимому,- определяется этими ловушками, а не зарядом в диэлектрике, как в случае МОП-ПТ.
Меняя условия испарения и конденсации слоев, образующих
ППТ, можно изготавливать приборы разных типов. Например, при использовании сульфида кадмия и моноокиси кремния в зависимости от давления остаточных газов в вакуумной камере могут быть получены приборы как с индуцированным, так и со встроенным каналом.
Рис. 11. Схематическое изображение пленочного полевого транзистора
Считается, что транзисторы, описанные Ваймером [23], работают в режиме аккумуляции, а не инверсии, т. е. канал имеет тот же тип проводимости, что и полупроводник.
Статические характеристики ППТ сходны с характеристиками соответствующих типов МОП-ПТ. Нередко, однако, крутизна ППТ оказывается частотно-зависящей даже при низких частотах. Кроме того, наблюдается дрейф характеристик ППТ со временем, температурой и иногда от приложенного постоянного напряжения. Эти нежелательные эффекты обусловлены недостаточной пассивацией приборов.
Теория работы ППТ еще окончательно не разработана. Установлено, однако, что упрощенная теория МОП-ПТ, рассмотренная выше, весьма удовлетворительно согласуется с данными экспериментального исследования ППТ.
Другой разновидностью ППТ являются приборы, изготовленные на основе монокристаллических полупроводниковых пленок. В работах [20, 21, 24] описаны транзисторы такого типа, полученные эпитаксиальным наращиванием кремния на сапфировую подложку. Транзисторы с индуцированным каналом [24] имеют выпрямляющие контакты истока и стока (§ 2.5); в приборах с глубоким обеднением [20, 21] используются омические контакты, модуляция проводимости осуществляется изменением толщины проводящего канала. Преимуществом ППТ на основе монокристаллических пленок полупроводника является возможность их пассивации, обеспечивающей большую стабильность параметров.
Глава 2 Физические основы полевого эффекта
2.1 Дрейфовый ток в полупроводниках
Электрический ток дрейфа представляет собой поток заряженных частиц в данной точке пространства. Заряженными частицами могут быть электроны или дырки. Для удобства будем считать, что ток переносится только электронами.
Предположим, что все электроны, создающие в полупроводнике ток, имеют некоторую среднюю скорость < v >. Закон Ома для этого случая выглядит так
J = σE (17)
где J- плотность тока, σ- удельная электропроводность материала, Е- напряженность электрического поля.
Плотность тока представляет собой заряд, протекающий через единичную площадку полупроводникового материала в единицу времени.
Таким образом
J=dq/dtds (18)
J=ne
где n - объемная концентрация электронов в материале, e- заряд электрона.
При наличии электрического поля скорость пробега электронов увеличивается под действием электростатической силы. Однако ускорение электронов не может продолжаться бесконечно, так как в противном случае их скорость линейно возрастала бы со временем, что привело бы к увеличению плотности тока при постоянном напряжении. Практически это не осуществимо. Поэтому введем предположение о существовании некоторой «силы трения», стремящейся замедлить движение электронов и ограничить их скорость.
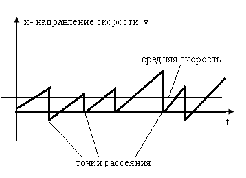
Рисунок 12.
Сила трения представляет собой процесс рассеяния электронов. Электрическое поле ускоряет движение электронов до тех пор, пока они не столкнутся с атомами кристаллической решетки, совершающими тепловые колебания, или с ионизированными атомами примеси. Рассеяние может происходить в любом направлении. Однако, считая модель рассеяния одномерной, можно показать, что каждый единичный процесс рассеяния в заданный момент времени сводит скорость электронов к некоторой средней величине. Характер рассеяния иллюстрируется на рисунке 12. Процессы рассеяния в полупроводниковых материалах можно разделить на две основные категории: на тепловых колебаниях кристаллической решетки и на ионизированных атомах примеси.
Наличие этих двух механизмов рассеяния вызывает появление силы трения. Рассмотрим одномерную модель и предположим, что сила трения действует в направлении, обратном движению электрона, и пропорциональна его скорости:
Fтр= -R
где R- постоянная величина.
Когда скорость электронов достигает предельной величины, средняя сила, действующая на них, должна равняться нулю. Следовательно, сила трения при достижении электронами максимальной скорости, должна равняться силе, действующей со стороны приложенного электрического поля, поскольку они направлены в противоположные стороны:
R
Из (17) и (19) следует, что
E=ne
Подставляя это выражение в (21) и проведя соответствующие преобразования, получаем
R=ne2/τ (22)
Сила трения может быть определена по формуле
F=-m
где m - масса электрона; τ- среднее время свободного пробега между последовательными столкновениями.
Определенная таким образом сила трения, представляет собой произведение массы электрона на ускорение.
Приравняв правые части равенств (21) и (23), получим выражение для проводимости материала, обусловленное только проводимостью электронов:
σ= ne2τ/m. (24)
Следует отметить, что весь проведенный анализ проводится в предположении, что в выражении для закона Ома используется постоянная скорость электронов, а не постоянное ускорение.
Равенство (24) можно представить в виде
σ=ne(eτ)/m, (25)
то тогда можно определить подвижность электронов
μ= (eτ/m). (24)
В системе СGS размерность подвижности будет 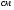 2
2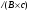 . Ранее было показано, что
. Ранее было показано, что
Ј=ne<v>=σE=ne(eτ/m)E,
следовательно,
Определяемая формулой (25) скорость есть дрейфовая скорость, равная произведению подвижности электрона на напряженность электрического поля.
Подвижность электрона характеризует «степень легкости», с которой электрон перемещается в кристаллической решетке под действием электрического поля. При комнатной температуре дрейфовая скорость значительно меньше тепловой. Но так как направление тепловых скоростей для различных электронов является не упорядоченным, то возникающий ток в основном будет определяться дрейфовой составляющей, направленной вдоль вектора напряженности электрического поля.
Подвижность электронов и дырок в кристаллической решетке является функцией рассеяния в результате тепловых колебаний узлов кристаллической решетки рассеяния на ионизированных атомах примеси. Поэтому, прежде чем вычислить подвижность, необходимо принять во внимание концентрацию легирующей примеси. В общем случае дрейфовая подвижность μ связана с подвижностью, обусловленной рассеянием электронов (дырок) на тепловых колебаниях узлов кристаллической решетки μт, и с подвижностью, обусловленной рассеянием на ионизированных атомах примеси μп, по следующему закону:
1/ μ=1 / μт + 1 / μп. (26)
Дрейфовые скорости электронов и дырок соответственно равны
v дрn=-μ nE,
v дрp=μ pE.
Знак минус в выражении для дрейфовой скорости электронов указывает, что электроны перемещаются в направлении, противоположном направлению действующего поля, а дырок – в направлении действия поля. Через μт и μп обозначены подвижности электронов и дырок.
Предположим, что к полупроводниковому образцу длиной l и поперечным сечением А приложено напряжение U(рисунок 13). Если концентрация электронов в объеме полупроводника равняется n, а концентрация дырок - p, то в направлении, противоположном направлении поля, дрейфует заряд плотностью – en, а в направлении поля – заряд плотностью ep.
Рисунок 13
Дырочная и электронная составляющие плотности тока представлены следующими выражениями:
Јn=-envдр n , (27 а)
Јp=envдр p. (27 б)
Общая плотность тока равняется сумме дырочной и электронной составляющей, т. е.
Ј=Јn+Јp=-envдрn+epvдрp.
Но так как
v дрn=-μ nE,
v дрp=μ pE,
то плотность тока, полученная в результате суммирования дырочной и электронной составляющих, примет вид
Ј=eE(μ nn+μ pp). (28)
Напряженность электрического поля в образце:
E=U/l.
Умножим левую и правую части соотношения (14) на площадь поперечного сечения А, получим суммарный ток
I=eUA(μ nn+μ pp)/l . (29)
Из закона Ома для участка электрической цепи U=IR можно найти сопротивление полупроводникового образца
R=l/eA (μ nn+μ pp). (30)
Сопротивление образца (рисунок 2)
R=ρl/A, где ρ- удельное сопротивление материала, равное
ρ= 1/σ=1/e(μ nn+μ pp). (31)
2.2 Диффузионные токи в полупроводниках
Диффузионный ток возникает из-за неравномерного распределения носителей заряда. Плотность тока Ј=σE вызвана только дрейфом носителей, и ее существование предполагает равномерное распределение дырок и электронов в разрешенных зонах. В случае не равномерного распределения появляется градиент концентрации и возникает диффузионный ток. В самом общем случае для одномерной модели составляющие плотностей диффузионных токов дырок и электронов равны
Јpx=-e Dpdp/dx, (32)
Јnx=e Dndp/dx, (33)
где Dp и Dn- соответствующие коэффициенты диффузии электронов и дырок, связанные с подвижностью соотношением Эйнштейна:
Dn=μnkT/e , (34)
Dp= μpkT/e , (35)
где k- постоянная Больцмана; T- абсолютная температура в Кельвина.
Так как плотность в полупроводнике является суммой дрейфовой и диффузионной составляющих, то для одномерной модели имеем
Јобщ=σEx+e(Dndn/dx-Dpdp/dx). (36)
Для трехмерной модели это выражение приобретает следующий вид:
Јобщ=σE+e(Dn-Dp). (37)
2.3 Зависимость эффективной подвижности электронов в канале от напряжения на затворе
При выводе выражений для электрических параметров МДП-транзистора будем считать, что подвижность носителей тока в канале не зависит от напряжения на затворе. Это условие справедливо не всегда, особенно при малом и большом напряжениях на затворе. В общем случае справедливость предположения о постоянстве подвижности носителей будет зависеть от физической структуры границы раздела кремний — диэлектрик. Если на границе раздела этих двух областей имеется большое количество ловушек, то дрейфовая подвижность в канале будет резко уменьшаться при низких напряжениях на затворе. Этот эффект легко объясним. Если затвор имеет небольшой положительный потенциал относительно подложки, то из объема материала р-типа по направлению к границе раздела кремний — диэлектрик притягивается небольшое количество электронов. Большинство этих электронов захватывается ловушками, т. е. электроны становятся неподвижными. Следовательно, в этом случае можно говорить только о некоторой эффективной подвижности электронов в области канала, которая, очевидно, меньше обычной подвижности, определенной для объема полупроводника.
Введем следующие обозначения: n — концентрация электронов в области канала; nt — концентрация захваченных электронов в области канала; n—nt — концентрация свободных электронов в области канала; µn — дрейфовая подвижность электронов в подложке. Тогда эффективная дрейфовая подвижность в области канала
µэфn=µn(n-nt)/n+µзахв(nt/n)
Для электронов, локализованных на ловушках,
µзахв=0
Следовательно, эффективная подвижность электронов в области канала
µэфn=µn((n-nt)/n)
Поскольку
(n—nt)/n<1,
то
µэфn<µn
На практике вследствие вторичных эффектов эффективная подвижность при средних напряжениях на затворе немного меньше, чем в объеме.
При возрастании положительного потенциала на затворе количество электронов, поступивших из подложки р-типа, возрастает, и они притягиваются в область канала. Оставшиеся свободными ловушки быстро заполняются, и, в конечном счете, концентрация свободных электронов в канале значительно превысит концентрацию электронов, локализованных на ловушках.
При более высоких напряжениях на затворе n>>nt, и теоретически эффективная подвижность приблизится к величине объемной подвижности. При больших напряжениях на затворе µэфn приближается к µп.
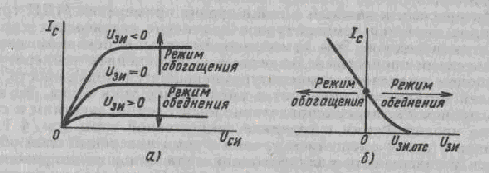
Для транзистора с каналом n-типа с обогащением ток между стоком и истоком появляется при положительном потенциале на затворе, составляющем несколько вольт. Так называемое пороговое напряжение соответствует началу процесса захвата электронов, втянутых в область канала по поверхностным ловушкам. Дальнейшее увеличение концентрации свободных электронов в области канала не будет происходить до тех пор, пока большинство ловушек не заполнится. Транзистор с каналом р-типа обычно имеет более высокое пороговое напряжение, чем аналогичный транзистор с каналом n-типа. Действительно, если у поверхности «кремния существует начальный канал n-типа, то он обедняется раньше, чем. в этой области создается достаточная концентрация дырок. Кроме того, дырки, так же как и электроны, захватываются поверхностными ловушками.
При высоких напряжениях на затворе предположение о постоянстве подвижности нарушается. При низких напряжениях на затворе подвижность носителей уменьшается. Однако механизм этого явления совершенно другой. Толщина диэлектрического слоя, находящегося между затвором и подложкой, настолько мала, что при высоких напряжениях на затворе поле затвора обычно превышает 106 в/см. Если напряженность поля в диэлектрике достаточно высока, то на носители тока, протекающего в канале между стоком и истоком, действует сила, оттесняющая их к границе раздела диэлектрик— полупроводник, которая непрерывно отражает носители. Если граница раздела представляет собой настолько идеальную плоскость, что до и после столкновения носителей момент их движения остается постоянным, подвижность носителей также не изменяется.
Однако на практике это происходит редко, так как граница раздела между двумя материалами обычно имеет неровности и несовершенства. Чем менее ровная граница и чем больше дефектов она имеет, тем более хаотичным будет движение электронов после столкновения. Это вызывает появление другого механизма рассеяния, что приводит к уменьшению подвижности носителей точно таким же образом, как при рассеянии на тепловых колебаниях кристаллической решетки и ионизированных атомах примеси. Последние достижения в области технологии полупроводниковых материалов позволили улучшить качество подготовки поверхности полупроводниковых пластин. Благодаря этому незначительное уменьшение подвижности носителей при больших напряжениях на затворе не оказывает влияния на работу большинства типов МДП-транзисторов, выпускаемых в настоящее время промышленностью. Обычно характеристики МДП-транзисторов при высоких напряжениях на затворе ухудшаются. Часто это обусловлено существованием сопротивления, которое ослабляет любой эффект, приводящий к уменьшению подвижности.
2.4 Поверхность полупроводников
Явление изменения концентрации свободных носителей в приповерхностной области полупроводника за счет внешнего электрического поля называется эффектом поля.
Данное явление можно наблюдать например в системе металл – диэлектрик – полупроводник (МДП)(рисунок 14) .
На металл подается оложительное напряжение или отрицательный потенциал, равный по значению, но противоположный по знаку заряду на металлической пластине. Заряд в полупроводнике не находится на поверхности, а сосредотачивается в приповерхностном слое. Если в металлах, имеющих очень высокую концентрацию носителей заряда (~1028м-3), нейтрализация поверхностного заряда происходит уже на расстоянии, равном нескольким параметрам решетки, то в полупроводниках область объемного заряда простирается на значительную глубину (~ 10-6 м и более). Обычно её принимают равной так называемой дебаевской длине экранирования LD, определяемой как расстояние, на протяжении которого потенциал поля в веществе со свободными носителями заряда уменьшается в e раз (e≈ 2.72). Расчеты показывают, что для собственного полупроводника
LD=(εε0kT/2e2ni) ½ =(εε0φΤ/2eni) ½ (38)
где ε - относительная диэлектрическая проницаемость полупроводника; ε0 - электрическая постоянная вакуума; φΤ= kT /e – температурный потенциал; e - заряд электрона.
Для примесного полупроводника с концентрацией ионизированной примеси N
LD= (εε0φΤ / eN) ½ . (39)
Поскольку N » ni, значение LD в примесных полупроводниках много меньше, чем в собственных. Например, в собственном кремнии LD ≈ 14 мкм, а в примесных кремнии с NД = 1022 м-3 LD ≈ 0.04 мкм при температуре Т= 300 К.
Заряжение поверхности полупроводника вызывает возникновение разности потенциалов между его поверхностью и объемом. Следствием этого является искривление энергетических зон у поверхности.
При заряжении поверхности отрицательным зарядом энергетические зоны изгибаются вверх, так как при перемещении электрона из объёма к поверхности его энергия увеличивается. При заряжении поверхности положительным зарядом зоны изгибаются вниз. Изгиб простирается в глубь полупроводника примерно на величину LD.
2.5 Электромагнитная теория и полевой эффект
Если рассматривать уравнения Максвелла в дифференциальной форме при соответствующих граничных условиях, то физический механизм полевого эффекта на поверхности полупроводника становится понятным. Одно из важнейших уравнений электромагнитной теории записывается как ε
Div D=div(εE)=ρ (40)
где D – вектор электрического смещения; ε – диэлектрическая проницаемость материала; Е – напряженность электрического поля; ρ – объемная плотность электрического заряда.
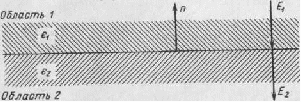
Таким образом, дивергенция вектора электрического смещения равна объемной плотности заряда. Этот закон будет соблюдаться в любой точке объема исследуемого материала. Однако па границе раздела двух разнородных материалов или на поверхности исследуемого полупроводника возникает электрический заряд. Тогда в этом месте электрическое поле претерпевает разрыв, величину которого можно вычислить, исходя из определенных граничных условий. Из рис. 15 видно, что на границе раздела между двумя областями 1 и 2 существует поверхностный заряд. Плотность поверхностного заряда равняется величине разрыва вектора электрического смещения, перпендикулярного к поверхности пластины. Если σ есть плотность поверхностного заряда на единицу площади на границе раздела, a n — единичный вектор, направленный перпендикулярно к границе раздела в сторону области 2, то граничным условием будет
(ε1E1 – ε2E2)n = σ. (41)
Условия, аналогичные изображенным на рис., существуют в МДП-транзисторах на границе раздела кремний — двуокись кремния. Рассмотрим транзистор с каналом n-типа, на затвор которого подано положительное напряжение, а между истоком и стоком смещение отсутствует. Вследствие большого различия удельных сопротивлений обоих материалов падение напряжения на участке между затвором и подложкой происходит полностью в слое окисла, и практически во всех случаях электрическое поле в кремнии будет отсутствовать.
Учитывая граничные условия, получим
[εSiO2E – εSi(0)]n = σ (42)
Где E и n имеют прямо противоположные направления, а произведение в скобках – отрицательный знак. Следовательно,
σ = – εSiO2E. (43)
При подаче за затвор МДП-транзистора положительного смещения происходит электростатическое притягивание отрицательных зарядов, и параллельно поверхности кремния образуется отрицательно заряженный слой. Таким образом, между истоком и стоком появляется токопроводящий канал n-типа. Если между затвором и подложкой приложено отрицательное напряжение, то вектор напряженности электрического поля в диэлектрике имеет противоположное направление.
При этом у поверхности кремния должен образоваться положительно заряженный слой, или канал с проводимостью n-типа. Тем самым граничные условия были бы полностью соблюдены.
Можно считать, что эффект поля на поверхности полупроводников является прямым следствием фундаментальных законов электромагнитной теории.
2.6 Статистика Ферми
Для нахождения концентрации основных и неосновных носителей в кристаллической решетке полупроводника в состоянии равновесия применяется статистика Ферми.
Электронная проводимость в полупроводниковых материалах создается за счет переноса носителей, находящихся в зоне проводимости и валентной зоне. В действительности эти зоны представляют собой спектр энергетических состояний, в которых электрон может находиться при перемещении в кристаллической решетке. Зона проводимости имеет более высокий энергетический уровень, чем валентная зона, и поэтому при данной температуре является менее заполненной. Зоны разделяются энергетическим промежутком, называемым запрещенной зоной.
При нормальных условиях электрон, находящийся в кристаллической решетке, не может занимать энергетические уровни, расположенные в запрещенной зоне. Энергетический промежуток между самым высоким разрешенным состоянием в валентной зоне и самым низким разрешенным состоянием в зоне проводимости называется шириной запрещенной зоны. Для разных полупроводниковых материалов она имеет разное значение.
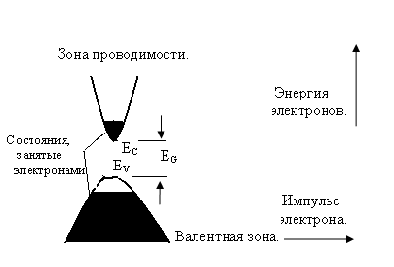
Упрощенная модель распределения электронов по энергетическим состояниям в зоне проводимости и в валентной зоне показана на рисунке 17 Обычно экстремумы двух зон в импульсном пространстве смещены относительно друг друга. Исключением составляют проводники с прямыми переходами.
Электроны, заполняющие состояния в зоне проводимости, и дырки при приложении внешнего электрического поля свободно перемещаются, вызывая прохождение тока. Оба типа носителей присутствуют одновременно во всех полупроводниках. Применяя статистику Ферми, можно вычислить равновесные концентрации как основных, так и не основных носителей, находящихся в кристаллической решетке.
Рисунок 17 .Зонная структура полупроводника с прямыми переходами.
Функцию распределения Ферми записывают как
f (E)=1/1+exp[(E-)/kt]. (44)
Функция Ферми определяет вероятность того, что данное состояние с энергией Е занято электроном. Величина EF , называемая энергией или уровнем Ферми. Уровень Ферми характеризует связь объемных свойств полупроводникового материала с вакуумом и является постоянным. Если известная зависимость плотности состояний в зоне проводимости и валентной зоне от энергии, то положение уровня Ферми даст возможность определить количество электронов, находящихся в данных энергетических состояниях, и количество вакантных состояний.
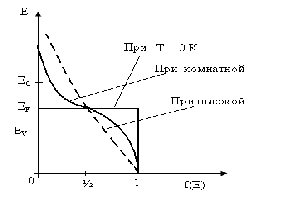
Рисунок 18.Поведение функции Ферми при изменении температуры.
Интегрирование в пределах обеих зон даст концентрацию электронов в зоне проводимости и концентрацию дырок в валентной зоне полупроводника. Поведение функции Ферми при изменении температуры показано на рисунке 18.
Из рисунка 18 следует, что уровень Ферми обычно лежит в запрещенной зоне между валентной зоной и зоной проводимости. При легировании кремния атомами примеси, имеющей пять валентных (кремний имеет четыре валентных электрона), в зоне проводимости кремния появляется лишний электрон. Материал приобретает проводимость n- типа, и уровень Ферми перемещается в сторону самого нижнего энергетического уровня зоны проводимости EC . Этот тип примесей называется донорным. Аналогичным образом, когда вводится примесь, атомы которой имеют только три валентных электрона (акцепторы), они ионизируются электронами валентной зоны, и появляются дырки. Полупроводник приобретает проводимость p – типа, и уровень Ферми сдвигается в сторону энергетического потолка валентной зоны ЕV.
После интегрирования по энергетическим уровням обеих зон получаем следующие выражения:
n = NCexp[-(EC-EF)/kT] (45)
p = NVexp[-(EF-EV)/kT], (46)
где NC и NV – соответственно плотности состояний в зоне проводимости и валентной зоне.
Перемножив, левые и правые части (45) и (46), получим произведение концентраций неосновных и основных носителей тока для одного и того же материала. Величина этого произведения не зависит от положения уровня Фермии, следовательно, от концентрации легирующей примеси:
np= NCNVexp (EV- EC)/ kT =NCNVexp(-∆E/kT), (47)
где NCNVexp(-∆E/kT)
представляет собой постоянную, которая зависит от температуры и обычно обозначается как n2i (квадрат концентрации собственных носителей в чистом материале). Таким образом,
np= n2i. (48)
Следовательно, концентрация собственных носителей равна
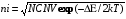 (49)
(49)
Если энергию ЕV принять за исходный уровень, то есть положить её равной нулю, то энергия Ферми выразится произведением отрицательного заряда электрона на соответствующий потенциал Ферми
EF= - eφF [эв]. (50)
Считая, что середина запрещенной зоны соответствует собственному потенциалу ψ, для которого
½ ∆E= - e ψ [эв], (51)
определим концентрацию подвижных носителей в материале
n= ni expe[(ψ-φE )/kT], (52)
p=niexpe[(φE-ψ)/kT]. (53)
При комнатной температуре в случае кремния n – типа все донорные примеси ионизированы, и концентрация электронов в зоне проводимости будет приблизительно равна концентрации легирующей донорной примеси
nn≈NД . (54)
Подставляя (48) в (50), получаем концентрацию неосновных дырок
pn≈n2i/NД. (55)
Аналогично можно предположить, что в кремнии p – типа при комнатной температуре все акцепторные примеси ионизированы, и концентрация будет дырок приблизительно соответствовать концентрации легирующей примеси Na, то есть
pp≈Na. (56)
Снова используя равенство (44), получаем концентрацию неосновных электронов
np≈ni2/Na. (57)
Из сказанного можно сделать вывод, что если в приповерхностной области полупроводника середина запрещенной зоны Еi располагается ниже уровня Ферми, концентрации n> ni> n,то полупроводник в этой области обладает электропроводностью n- типа. В области, в которой середина запрещенной зоны Еi располагается выше уровня Ферми, концентрации p>ni>n,то полупроводник в этой области имеет электропроводность p – типа. В области, в которой уровень Ферми и середина запрещенной зоны Еi совпадают, концентрации n=p=ni, то полупроводник ведет себя как собственный.
2.7 Образование обедненных, инверсионных и обогащенных слоев в полупроводнике
За счет внешнего электрического поля можно получить обедненные, инверсионные и обогащенные слои в приповерхностной области полупроводника.
Так как работа МДП-транзистора зависит от образования проводящего инверсионного слоя на поверхности кремниевой пластины, то его характеристики в значительной степени будут зависеть от природы поверхности. Переход электрона из полупроводника в диэлектрик определяется свойствами границы раздела кремний — двуокись кремния, которые, в свою очередь, зависят от многих объемных параметров полупроводника. Известно, что энергетический уровень ловушек, находящихся на поверхности материала, расположен в запрещенной зоне. При описании характеристик МДП-транзисторов необходимо учитывать эти состояния. Предположение о существовании поверхностных состояний, энергетический уровень которых расположен 'В запрещенной зоне полупроводника, впервые высказано в работе. Эти состояния можно разделить на две категории: состояния, расположенные в слое двуокиси кремния, и состояния, расположенные на границе раздела диэлектрик — полупроводник. Каждый тип состояний обусловлен соответствующим видом взаимодействия. Состояния, расположенные в слое двуокиси кремния, чрезвычайно чувствительны к окружающей среде (влаге, температурным градиентам и т. д.) и, как считают, обусловлены адсорбцией ионов и молекул тонким слоем окисла, покрывающим поверхность полупроводниковых приборов. Состояния, расположенные на границе раздела кремний — двуокись кремния, менее чувствительны к окружающей среде и зависят от качества обработки поверхности пластины кремния и процесса выращивания окисла. Таким образом, любые несовершенства, образующиеся при химическом травлении поверхности полупроводникового материала, отразятся «а плотности поверхностных состояний.
Рассмотрим еще раз слабо легированную пластину p-типа и исследуем область канала, над которой имеется слой двуокиси кремния. Первоначальный инверсионный слой (при U3=0) сильнее зависит от адсорбированного окислом заряда, чем от состояний на границе раздела диэлектрик — полупроводник. Если предположить, что в слое двуокиси кремния имеются захваченные заряды положительных ионов, то у поверхности кремния будет образовываться сложный заряженный слой, состоящий из свободных электронов, находящихся в инверсионном слое, ионизированных акцепторов в обедненном слое и области постепенного перехода от поверхности к объему кремния р-типа. Однако в этих условиях электрическое поле Е отсутствует. Как мы увидим дальше, положительные заряды в слое двуокиси кремния вызывают образование первоначального инверсионного слоя (при нулевом напряжении на затворе).
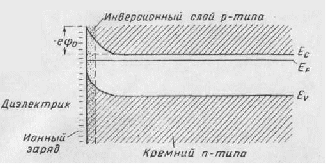
Распределение заряда в разных случаях может быть различным. Рассмотрим некоторые из них. Слой положительных зарядов в окисле вызывает образование слоя отрицательных зарядов на поверхности кремния. Свободные электроны вытягиваются из объема полупроводника р-типа, где они были неосновными носителями, и концентрируются вблизи границы раздела диэлектрик — полупроводник. Однако электроны не в состоянии преодолеть границу раздела, поскольку их энергия для этого недостаточна. Непосредственно под границей раздела такие свободные электроны образуют проводящий инверсионный слой n-типа. Последующие электроны, которые притягиваются слоем положительных зарядов, рекомбинируют в объеме материала, образуя область ионизированных акцепторных атомов, или обедненный слой. Так как обедненный слой состоит только из ионизированных атомов и в нем нет свободных носителей тока, то область, расположенная под инверсионным слоем, не обладает проводимостью. При дальнейшем удалении от поверхности все большую роль начинают играть объемные свойства полупроводникового материала р-типа. Очевидно, что между инверсионным и обедненным слоями, а также между обедненным слоем и объемом полупроводника нет резкой границы. Такие границы являются размытыми, а резкой является только граница раздела полупроводник — диэлектрик, отделяющая инверсионный слой n-типа от положительного заряда ионов в слое окисла.
Диэлектрик
Рисунок 20. Искривление зон у поверхности полупроводника n-типа (Ψ0 — поверхностный потенциал).
Это перераспределение зарядов на поверхности полупроводника, защищенного слоем окисла, оказывает влияние на положение уровня Ферми в этой области. Уровень Ферми в объеме кремния р-типа находится у потолка валентной зоны, a в инверсионном слое кремния n-типа он должен располагаться у дна зоны проводимости. Система находится в равновесии, и применение уровней Ферми справедливо. Уровень Ферми может быть уподоблен химическому потенциалу и устанавливает связь между свойствами частиц, находящихся в объеме материала и в вакууме. Особенность уровня Ферми состоит в том, что он должен оставаться постоянным во всех областях материала. Если уровень Ферми постоянен, то у поверхности полупроводника должно происходить искривление зон. Это показано на рис. 19 сверху для кремния р-типа и на рис. 20 сверху – для кремния n-типа. Отрицательный заряд, захваченный ловушками, показан только на рис. 20 сверху.
Другой механизм, способствующий образованию первоначального n-канала — разность работ выхода кремния, двуокиси кремния и материала электрода затвора. Сначала рассмотрим искривление зон на границе раздела полупроводник — диэлектрик, вызванное разностью работ выхода кремния и двуокиси кремния.
Рисунок 21 Определение работы выхода электрона (еφχ— произведение работы выхода на заряд электрона)
Работа выхода материала определяется энергией, необходимой для удаления электрона с уровня Ферми в вакуум.
Таким образом, работа выхода материала χ равна eφχ (см. рис.21).
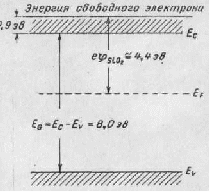
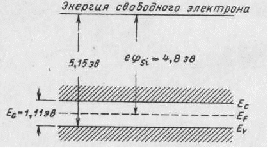
Работа выхода кремния р-типа в среднем равняется 4,8 эв. Так как уровень Ферми в кремнии р-типа зависит от концентрации легирующей акцепторной примеси, то работа выхода также будет зависеть от концентрации легирующей примеси. Разница между энергией свободного электрона и энергией дырок, расположенных у потолка валентной зоны кремния, составляет 5,15 эв. Ширина запрещенной зоны кремния хорошо известна и при комнатной температуре равняется 1,11 эв. Таким образом, энергетическая диаграмма кремния р-типа приняла бы вид, показанный на рис.22.
Рисунок 22 Энергетическая диаграмма кремния.
Работа выхода электронов из кремния обозначается как eφS1.
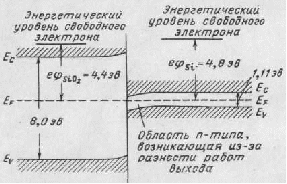
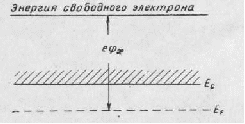
Если не учитывать влияния поверхностных эффектов, то энергетическая структура двуокиси кремния примет вид, показанный на рис23.
Рисунок 23 Энергетическая диаграмма двуокиси кремния.
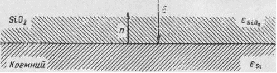
Рисунок 24 Искривление зон на границе раздела кремний — двуокись кремния, происходящее вследствие разницы работ выхода.
Работа выхода двуокиси кремния для пленок [I] толщиной от 1500 до 6 000 Å, составляет 4,4 — 4,5 эв. Работа выхода φSiO2 также показана на рис12. сверху. Предположим, что кремний и двуокись кремния контактируют друг с другом и образуют границу раздела. Если энергетические диаграммы, показанные на двух рисунках сверху, совместить в состоянии равновесия, то уровень Ферми должен оставаться постоянным в обеих областях. Для поддержания равновесия, при котором через границу раздела не протекал бы ток, необходимо учесть разность работ выхода кремния и двуокиси кремния. Это приводит к изгибу зон у границы раздела. Так как работа выхода кремния больше, чем двуокиси кремния, то изгиб зон в кремнии всегда будет происходить так, что на его поверхности образуется канал n-типа. Величина потенциального барьера, возникающего на границе раздела, достаточна для того, чтобы ток между двумя областями отсутствовал. Это показано на энергетической диаграмме рис 23. Отметим, что если какой-нибудь диэлектрик имеет работу выхода, большую, чем работа выхода кремния, образуется поверхностный канал с проводимостью р-типа.
Известно, что разные материалы имеют разные энергии свободных электронов.
Как показано на рис13. энергии свободных электронов для двух разных материалов не совпадают. Однако так называемая энергия свободного электрона не равна полной энергии электрона, изолированного от всяких взаимодействий. Эту энергию необходимо рассматривать как добавочную энергию, необходимую электрону, находящемуся на уровне Ферми в материале данного типа, для того чтобы он мог преодолеть потенциальный барьер и попасть в вакуум. Каждый материал характеризуется собственными силами связи. Следовательно, энергия свободного электрона будет разной для разных материалов. В состоянии равновесия единственной величиной, связывающей объемные свойства материала с вакуумом, является уровень Ферми. Все виды энергии кристаллической решетки будут выражаться через уровень Ферми, кроме энергии электронов, находящихся в вакууме.
Величина канала на поверхности кремния зависит от разности работ выхода кремния и двуокиси кремния, и, кроме того, определяется работой выхода металла, из которого выполнен электрод затвора. Особенно это важно в случае тонких окислов. Достаточно отметить, что металлы с малой работой выхода способствуют возникновению канала на поверхности кремния, тогда как металлы с работой выхода, превышающей работу выхода кремния, приводят к уменьшению канала.
Глава 3 Применение полевого эффекта
3.1 Полевые транзисторы
Полевой транзистор – это полупроводниковый прибор, усилительные свойства которого обусловлены оттоком основных носителей, проходящим через проводящий канал и управляемым электрическим током.
Выделяют следующие виды полевых транзисторов: полевые транзисторы с управляющим переходом, с изолированным затвором.
Полевой транзистор с управляющим переходом – это полевой транзистор, управление потоком основных носителей в котором происходит с помощью выпрямляющего электрического перехода, смещенного в обратном направлении.
Полевой транзистор с изолированным затвором – это полевой транзистор, имеющий один или несколько затворов, электрически изолированных от проводящего канала[7,9].
3.2 Полевые транзисторы с изолированным затвором
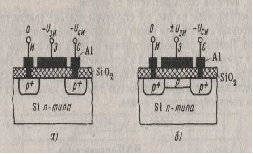
Структуры полевых транзисторов с изолированным затвором показаны на рисунке 25.
Рисунок 25. Структуры полевых транзисторов с изолированным затвором (с p - каналом): а – с индуцированным каналом, б – со встроенным каналом.
В кристалле полупроводника с относительно высоким удельным сопротивлением, который называют подложкой, созданы две сильнолегированные области с противоположным типом электропроводности. На эти области нанесены металлические электроды – исток и сток. Расстояние между сильно легированными областями истока и стока может составлять всего несколько микрометров. Поверхность кристалла полупроводника между истоком и стоком покрыта тонким (порядка 0,1 мкм) слоем диэлектрика. На слой диэлектрика нанесен металлический электрод – затвор. Получается структура, состоящая из слоя металла, диэлектрика и полупроводника, т.е. МДП-структура.
Полевой транзистор с изолированным затвором, в котором в качестве изоляционного слоя между металлическим затвором и проводящим каналом использован диэлектрик, называют полевым транзистором типа металл – диэлектрик – полупроводник или МДП-транзистор.
Выпрямляющие переходы под истоком и стоком могут быть выполнены в виде p-n- переходов, переходов Шотки, т.е. путем нанесения металлических электродов истока и стока непосредственно на подложку. Использование выпрямляющих переходов Шотки под истоком и стоком обеспечивает ряд преимуществ в технологии изготовления таких транзисторов, а так же улучшит их характеристики. Так, переходы Шотки имеют сравнительно малую толщину, что облегчает создание полевых транзисторов с очень коротким проводящим каналом.
Пока исходным полупроводником для полевых транзисторов с изолированным затвором в основном является кремний. Поэтому в качестве диэлектрика под затвором используется обычно слой диоксида кремния SiO2, выращенный на поверхности кристалла кремния путем высокотемпературного окисления.
Существует две разновидности МДП-транзисторов: с индуцированным каналом и со встроенным каналом.
В МДП-транзисторах с индуцированным каналом (рисунок 28 а), проводящий канал между сильнолегированным областями истока и стока и, следовательно, заметный ток стока появляются только при определенной полярности и при определенном значении напряжения на затворе относительно истока, которое называют пороговым напряжением(UЗИпор).
Изображенные на рисунке 28 структуры полевых транзисторов с изолированным затвором имеют подложку с электропроводностью n- типа. Поэтому сильнолегированные области под истоком и стоком, а так же индуцированный и встроенный канал имеют электропроводность p- типа. Если же аналогичные транзисторы созданы на подложке с электропроводностью p- типа, то канал у них будет иметь электропроводность n- типа[7,9].
3.3 МДП-транзистор с индуцированным каналом
Принцип действия. При напряжении на затворе относительно истока, равном нулю, и при наличии напряжения на стоке ток стока оказывается ничтожно малым. Он представляет собой обратный ток p-n- перехода между подложкой и сильнолегированной областью стока. При отрицательном потенциале на затворе (для структуры рисунок 28а) в результате проникновения электрического поля через диэлектрический слой в полупроводник при малых напряжениях на затворе (меньших UЗИ пор) у поверхности полупроводника под затвором возникают обедненный основными носителями заряда слой и область объемного заряда, состоящая из ионизированных нескомпенсированных примесных атомов. При напряжениях на затворе, больших порогового UЗИ пор, у поверхности полупроводника под затвором возникает инверсионный слой, который и является проводящим каналом между истоком и стоком. С изменением напряжения на затворе концентрация основных носителей заряда в проводящем канале, а так же, а так же толщина или поперечное сечение проводящего канала, т.е. происходит модуляция сопротивления проводящего канала. Основной причиной модуляции сопротивления проводящего канала в МДП-транзисторах с индуцированным каналом является изменение концентрации носителей заряда в проводящем канале; в полевых транзисторах с управляющим переходом – изменение толщины или поперечного сечения канала.
В связи с тем, что затвор отделен от подложки диэлектрическим слоем, ток в цепи ничтожно мал, мала мощность, потребляемая от источника сигнала в цепи затвора и необходимая для управления относительно большим током стока. Таким образом, МДП-транзистор с индуцированным каналом может производить усиление электрических сигналов по напряжению и по мощности.
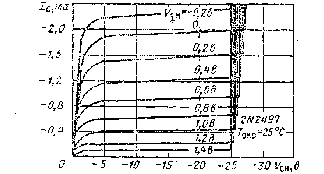
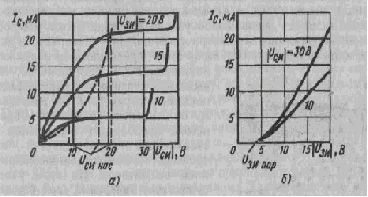
Выходные статические характеристики. Характер зависимости IС= f(UСИ) при UЗИ= const для МДП-транзистора с индуцированным каналом аналогичен характеру таких же зависимостей для полевого транзистора с управляющим переходом.
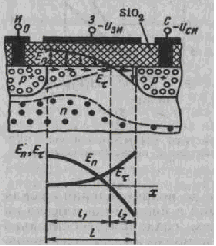
Рисунок 26. Выходные статические характеристики (а) и статические характеристики передачи (б) МДП-транзистора с индуцированным каналом[7].
Сулинейность крутых частей характеристик (рисунок 26 а) объясняется уменьшением толщины канала около стока при увеличении напряжения на стоке и неизменном напряжение на затворе, так как на сток и на затвор подаются потенциалы одного знака относительно истока. Следовательно, разность потенциалов между истоком и затвором или между затвором и прилегающей к стоку частью канала уменьшается. Поэтому при увеличении тока стока происходит уменьшение поперечного сечения канала около стока.
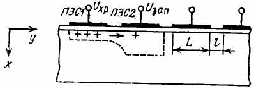
При напряжении насыщения UСИ НАС происходит перекрытие канала около стока и дальнейшее увеличение напряжения на стоке вызывает очень малое увеличение тока стока. Распределение напряженности электрического поля у поверхности полупроводника при напряжении на стоке, превышающем напряжение насыщения, т.е. для пологой части выходных характеристик, показано на рисунке 27. На расстоянии ι1 от сильнолегированной области истока преобладает нормальная составляющая напряженности электрического поля, созданная напряжением на затворе. На этом участке существует инверсионный слой у поверхности полупроводника. На расстоянии ι2 от сильнолегированной области стока преобладает касательная составляющая электрического поля, созданная напряжением на стоке относительно истока. Несмотря на то, что на участке канала протяженностью ι2 нормальная составляющая напряженности имеет другое направление и отталкивает дырки от поверхности полупроводника, через этот перекрытый участок канала идет ток, связанный с движением под действием сильного тянущего поля (касательной составляющей).
При увеличении напряжения на затворе (по абсолютному значению) выходные статические характеристики смещаются в область больших токов стока (рисунок 26 а), что легко понять на основе принципа действия МДП-транзистора, при этом может быть два вида пробоя: пробой p-n- перехода под стоком и пробой диэлектрика под затвором.
Статические характеристики передачи. Характер зависимости IС= f(UЗИ) при UСИ= const ясен из принципа действия МДП-транзистора с индуцированным каналом. Характеристики для разных напряжений на стоке выходят из оси абсцисс, соответствующей пороговому напряжению UЗИ ПОР (рисунок 26б). С увеличением напряжения на стоке при неизменном напряжении на затворе ток стока возрастает даже в пологой части статических характеристик (рисунок 26а), что приводит к смещению характеристик передачи вверх в выбранной системе координат.
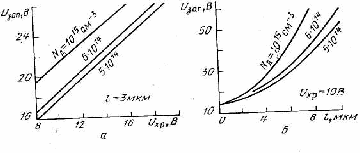
Интересным и важным с точки зрения применения МДП-транзисторов является температурное изменение статических характеристик передачи. С увеличением температуры в рабочем диапазоне температур уменьшается подвижность носителей заряда, что приводит к уменьшению тока стока. Так же происходит перераспределение носителей по энергиям и смещение уровней Ферми к середине запрещенной зоны. В связи с таким смещением уровня Ферми инверсионный слой образуется у поверхности полупроводника при меньших напряженностях электрического поля. Поэтому с увеличением температуры пороговое напряжение UЗИ ПОР уменьшается. В результате статические характеристики передачи для неизменного напряжения на стоке, но для разных температур пересекаются
Таким образом, температурные изменения тока стока при неизменных напряжениях на МДП-транзисторе могут быть как отрицательными, так и положительными; а также нулевыми в определенной рабочей точке статических характеристик. Обычно эффект температурной компенсации получается при напряжениях на затворе, не значительно превышающих пороговое напряжение UЗИ ПОР. Кроме того, еще надо учитывать, что крутизна характеристики S, определяющая усилительные свойства МДП-транзистора, изменяется с температурой даже при неизменном постоянном токе стока[9,7].
3.4 МДП-транзисторы со встроенным каналом
Проводящий канал под затвором МДП-транзистора может быть создан в результате локальной диффузии или ионной имплантации соответствующих примесей в приповерхностный слой подложки. Он может возникнуть из-за перераспределения примесей вблизи поверхности полупроводниковой подложки в процессе термического окисления ее поверхности. Наконец проводящий канал может появиться под затвором из-за фиксированного заряда в подзатворном слое диоксида кремния, на поверхностных энергетических уровнях, а так же из-за контактной разности потенциалов между металлом затвора и полупроводником подложки.
Модуляция сопротивления проводящего канала МДП-транзистора может происходить при изменении напряжения на затворе как положительной, так и отрицательной полярности.
Рисунок 29. Выходные статические характеристики (а) и статическая характеристика передачи (б) МДП-транзистора со встроенным p-каналом[7].
Таким образом, МДП-транзистор со встроенным каналом может работать в двух режимах: в режиме обогащения и в режиме обеднения канала носителей заряда. Эта особенность МДП-транзисторов со встроенным каналом отражается и на смещении выходных статических характеристик при изменении напряжения на затворе и его полярности (рисунок 29а).
Статические характеристики передачи (рисунок 29б) выходят из точки на оси абсцисс, соответствующей напряжению отсечки UЗИ ОТС, т. е. напряжению между затвором и истоком МДП-транзистора со встроенным каналом, работающего в режиме обеднения, при котором ток стока достигает заданного низкого значения[7]
3.5 Параметры и свойства полевых транзисторов с изолированным затвором
Основным параметром полевого транзистора с изолированным затвором, отражающим его усилительные свойства, является крутизна характеристики. Крутизна характеристики передачи при низкой частоте, соответствующая крутой части выходных статических характеристик, может быть определена по формуле
S = dI/dUЗИ│UСИ=const= (μpsCЗКb/l )UСИ. (55)
Для пологой части выходных статических характеристик крутизна характеристики передачи находиться следующим образом:
S'= (μpsCЗКb/ l) (UЗИ- UЗИ ПОР). (56)
где μps эффективная подвижность дырок в канале, CЗК- удельная емкость между затвором и каналом, b- ширина канала, l – длина канала.
Для увеличения крутизны характеристики исходный полупроводник должен обладать большей подвижностью носителей заряда. Транзистор с n-каналом имеет большее значение крутизны характеристики по сравнению с транзистором с p-каналом, так как подвижность электронов превышает обычно подвижность дырок.
Крутизна характеристики будет больше в полевых транзисторах с меньшей длиной канала. Нижний предел длины канала ограничен технологией изготовления. Обычно для изготовления полевых транзисторов с изолированным затвором применяют планарную технологию и метод фотолитографии, разрешающая способность которого не позволяет получать длину канала меньше 3-4 мкм.
Крутизну характеристики можно увеличить путем увеличения удельной емкости между затвором и каналом. Эта емкость определяется относительной диэлектрической проницаемостью и толщиной слоя диэлектрика под затвором. Использование диэлектрика с большей относительной диэлектрической проницаемостью приведет к увеличению крутизны характеристики, но одновременно увеличатся и паразитные емкости между затвором и стоком, что отрицательно повлияет на частотные свойства полевого транзистора. Уменьшение толщины слоя диэлектрика под затвором может также привести к недопустимому уменьшению пробивного напряжения этого слоя между затвором и стоком.
Физическая эквивалентная схема полевого транзистора с изолированным затвором аналогична физической эквивалентной схеме полевого транзистора с управляющим переходом.
Быстродействие полевых транзисторов с изолированным затвором определяется временем перезаряда распределенной емкости между затвором и каналом. Постоянные времени процесса перезарядки этой емкости при малом внешнем сопротивлении в цепи затвора ограничивают рабочий диапазон частот полевого транзистора с изолированным затвором частотами 10 ГГц, т.е. принципиально такие транзисторы могут работать приблизительно до тех же частот, что и биполярные транзисторы. Основной особенностью полевых транзисторов является очень большое входное сопротивление. Активная составляющая этого сопротивления может достигать 1015 Ом. Поэтому полевые транзисторы применяют в схемах, имеющих также большие сопротивления[9].
Глава 4 Характеристики полевого транзистора
4.1 Статические характеристики
Такие статические параметры, как ток насыщения стока при нулевом смещении на затворе и напряжение перекрытия канала Vнac позволяют получить значительную информацию о свойствах полевого транзистора. При расчете схем, в которых используются полевые транзисторы, именно эти две величины и являются самыми необходимыми. Что же касается остальных характеристик прибора (за исключением пробивного напряжения), то часто можно считать, что они обусловливают лишь эффекты второго порядка, и в большинстве случаев ими можно пренебречь.
Однако в ряде случаев бывает необходимо знать и некоторые другие статические характеристики полевого транзистора: ток утечки затвора, напряжение пробоя и статическое сопротивление между стоком и истоком.
Статическое сопротивление между стоком и истоком rс откр (измеренное при Vзи=0, Vси=0 и очень малом напряжении сигнала в цепи сток—исток, прикладываемом для измерения результирующего тока сигнала) следует рассматривать потому, что этот параметр важен при работе транзистора в качестве прерывателя и в схемах АРУ. Однако, как будет показано ниже в данной главе, величину rс откр легко подсчитать, зная 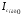 и Vнac
и Vнac
4.2 Величины Icнac0 и Vнac.
Семейство выходных характеристик полевого транзистора, приведенное на рис. 30, показывает зависимость тока IС от напряжения между стоком и истоком. Читатель сам может убедиться в том, что для режима насыщения можно считать ток стока приблизительно постоянным по величине. Особенности характеристики на участке пробоя будут рассмотрены ниже.
Рис. 30. Стоковые характеристики схемы с общим истокам.
Хотя ток 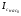 не очень сильно зависит от напряжения сток — исток, он, как показывает рис. 31, является ярко выраженной функцией температуры. Зависимость тока
не очень сильно зависит от напряжения сток — исток, он, как показывает рис. 31, является ярко выраженной функцией температуры. Зависимость тока 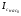 от температуры легко вывести из уравнения (1.17).
от температуры легко вывести из уравнения (1.17).
Дифференцируя это уравнение по температуре Т, будем иметь
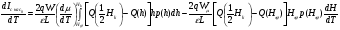 (2.1)
(2.1)
Два члена в правой части этого уравнения можно привести к гораздо более простой форме. Первый член запишем в виде , где есть по определению, температурный коэффициент подвижности носителей.
Рис. 31. Зависимость нормализованного тока стока при нулевом напряжении цепи затвор — исток от температуры окружающего воздуха. По длиной кривой можно также судить об изменении статического активного сопротивления цепи сток — исток в функции температуры.
Второй член можно упростить, разделив его на две части. Из уравнения (1.26)
(2,2)
При дифференцировании уравнения (1.9) по температуре можно установить, что единственным членом, зависящим от температуры, будет нижний предел интегрирования (при температурах выше 200° К можно считать, что все атомы примеси, ионизованы, и, следовательно, р(у) не зависит от температуры). В результате дифференцирования имеем
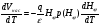 (2.3)
(2.3)
Если подставить эти соотношения в уравнение (2.1), то получится гораздо более простое выражение для 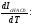
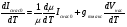 (2.4)
(2.4)
Используя выведенный в гл. 1 критерий качества М2, можно еще более упростить предыдущее уравнение:

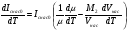 (2.5)
(2.5)
Из уравнения (2.5) видно, что 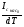 равно нулю при условии, что
равно нулю при условии, что
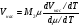 (2.6)
(2.6)
Это очень важный и полезный результат. Теперь остается только определить d/dT и dVнac/dT.
Кривые зависимости подвижности от температуры приводятся в нескольких источниках, наиболее известным из которых является [2.1]. Приведенные в этой книге кривые зависимости подвижности носителей в кремнии от температуры говорят о том, что в практически интересном диапазоне температур с довольно хорошим приближением можно считать
(2.7)
где n зависит от концентрации примесей. Тогда из уравнения (2.7) легко определить тот член, который нужно подставить в уравнение (2.5) вместо (1/) (d/dT), т. е. температурный коэффициент подвижности:
(2.8)
Уравнение (1.7) представляет собой общее выражение для напряжения, приложенного к обедненному слою в канале,. имеющему произвольную толщину; следовательно, можно писать
(2.9)
Дифференцируя это выражение по температуре, получаем
(2.10)
Теперь из уравнения (2.3) следует, что
(2.11)
Таким образом, изменение напряжения перекрытия канала с температурой полностью определяется температурной зависимостью контактной разности потенциалов, т. е. в полевом транзисторе наблюдается точно такое же явление, как и то, которое вызывает изменение dVбэ/dT в плоскостных транзисторах. Величина является логарифмической функцией от абсолютной температуры и также логарифмически зависит от концентрации легирующих примесей по обе стороны р-n перехода.
Однако при исследовании свойств транзисторов вошло в практику пользоваться линейным приближением для выражения dVбэ/dT. При малых эмиттерных токах значение dVбэ/dT, равное примерно ±2,2 мв/град (в зависимости от того, какой тип прибора имеется в виду, р-n-р транзистор или n-p-n транзистор), считается вполне удовлетворительным приближением. Для наших целей такое приближение также можно считать достаточным, хотя в транзисторах, изготовляемых при помощи двойной диффузии, величина dVнас/dT ближе к —2 мв/град. Причина этого, вероятно, в том, что концентрации примесей в областях затвора и канала у полевого транзистора не равны соответствующим концентрациям в областях базы и эмиттера плоскостного транзистора обычного типа.
Возвращаясь к уравнению (2.6) и подставляя в него n/T вместо 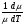 мы видим, что температурный коэффициент тока
мы видим, что температурный коэффициент тока 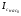 будет равен нулю у любого прибора, который удовлетворяет принятым нами допущениям и у которого напряжение перекрытия канала определяется выражением
будет равен нулю у любого прибора, который удовлетворяет принятым нами допущениям и у которого напряжение перекрытия канала определяется выражением
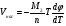 (2.12)
(2.12)
Теперь необходимо найти величину M2/n. Хорошим приближением для кремниевых полевых транзисторов, изготовляемых посредством двойной диффузии, является М2= –2. Мы могли бы воспользоваться значениями n, многократно упоминаемыми в литературе, однако эти значения лежат в пределах от 1,7 до 2,7, поскольку температурная зависимость подвижности зависит от концентрации примесей в исследуемом образце. Необходимо найти величину n, соответствующую концентрациям примесей, имеющихся обычно в канале полевого транзистора. Эту величину можно получить из графика зависимости от температуры для полевого транзистора с высоким напряжением . перекрытия канала, т. е. для такого прибора, у которого не оказывает заметного влияния на . Такой график приведен на рис. 32, и из него можно заключить, что хорошим приближением для n является значение 2. Это, конечно, очень удачно, так как при таком значении n с хорошим приближением можно считать, что M2/n= –1. Тогда при T = 300° К равно нулю у любого транзистора, у которого напряжение перекрытия канала равно 0,6 в.
Вообще говоря, величину Vнac трудно измерить непосредственно. Рассмотрим характеристики передачи, показанные на рис. 33. В масштабе рисунка трудно даже установить, где же отложено это .напряжение. Когда канал полностью перекрыт, в нем течет только небольшой ток утечки, и исследователю необходимо измерять медленно изменяющийся с напряжением очень небольшой по величине ток (составляющий иногда всего десятые доли наноампера) и определять, при каком значении напряжения затвор — исток этот ток перестает изменяться. Это настолько затруднительно, что целесообразнее определять величину Ушс косвенным путем, измеряя и gmмакс При одном и том же смещении и вводя в расчеты близкое к истинному значение М2. Например, для полевого транзистора, полученного с помощью двойной диффузии, М2= –2. Для приборов с квадратичной характеристикой напряжение Vнac можно также определять путем измерения напряжения Vзи при некотором токе стока, меньшем, чем ; величину Vнac при этом подсчитывают, пользуясь уравнением (1.54).
Удобной величиной для измерений является ток равный 1/10 тока ; расчетное значение напряжения перекрытия канала получается при этом равным
Vнac =1,46 Vзи при = 0,1
4.3 Зависимость тока насыщения стока от температуры
В предыдущем разделе мы видели, что ввиду противоположного действия температуры на подвижность носителей и на контактную разность потенциалов у полевого транзистора, напряжение Vнac которого равно примерно 0,6 в, температурный коэффициент тока равен нулю. Анализ температурной зависимости тока можно обобщить на любой ток насыщения стока, дифференцируя уравнение (1.14) по температуре так, как это было сделано в уравнении (2.1):
Ход преобразований при упрощении этого уравнения такой же, как и в случае уравнения (2.1). Как и ранее, первый член можно упростить путем простой подстановки; для упрощения второго члена вспомним, что поскольку Vзи представляет собой внешнее напряжение, то можно считать, что при исследовании величины оно остается постоянным. Тогда
(2.14)
Это означает, что
(2.15)
(2.16)
Поскольку мы можем поддерживать dVзи/dT равным нулю,
(2.17)
Следовательно, уравнение (2.13) приводится к виду
(2.18)
Воспользовавшись квадратичным приближением (1.54), уравнение (2.18) можно переписать, введя статические параметры и Vнac . Дифференцирование уравнения (1.54) по Vзи дает
(2.19-2.20)
Подставляя уравнения (2.20) и (2.8) в уравнение (2.18), получим
(2.21)
Уравнение (2.21) представляет собой выражение для температурного коэффициента тока стока при любом смещении. Нулевое значение температурного коэффициента имеет место, когда правая часть уравнения (2.21) равна нулю. Это произойдет при некотором значении тока , которое мы обозначим IcQ и которое будет равно
(2.22)
Где
(2.23)
Величины 0 и Vнас0 соответствуют некоторой начальной (отсчетной) температуре Т0. Следовательно, ток можно выразить через его значение I при отсчетной температуре:
(2.24)
Подставляя (2.24) в (2.22),. мы можем убедиться в том, что смещение, при котором температурный коэффициент равен нулю, очень слабо зависит от температуры:
(2.25)
Поскольку п приблизительно равно 2, абсолютная температура практически не входит в это уравнение. На рис. 33 приведены характеристики передачи одного конкретного полевого транзистора, снятые при трех различных температурах; видно, что ток IcQ, соответствующий точке пересечения характеристик, практически не зависит от температуры.
На рис. 34 построен график уравнения (2.25); сравнение этой кривой с экспериментальными данными, полученными на 24 образцах приборов, показывает, что использованный способ расчета дает вполне удовлетворительные результаты
Тот факт, что у полевого транзистора при некоторых условиях температурный коэффициент тока стока равен нулю, позволяет заключить, что этот прибор может хорошо работать в качестве усилителя постоянного тока.
Существует более удобная форма записи уравнения (2.21), в которой температурный коэффициент полевого транзистора выражен через dVзи/dT при постоянном Iс нас. Эта форма записи удобна, так как на практике принято указывать в качестве параметра усилителя постоянного тока величину изменения входного напряжения, необходимого для поддержания постоянным выходного сигнала. Производная dVзи/dT определяется таким же образом, как и производная в уравнении (2.21), за исключением того, что постоянным предполагается ток h нас, а не напряжение Vзи. Это равносильно тому, что полевой транзистор питается от источника стабильного тока. Алгебраические преобразования предоставляется провести читателю; окончательный результат имеет вид
(2.26)
Графики этого уравнения построены на рис 35, на них представлена зависимость dVзи /dT от Iс нас /Iс нас0, a Vнac служит текущим параметром. Точки пересечения оси абсцисс могут быть получены из уравнения (2.26); например, dVзи /dT = 0 при Vнac = 0,6 в и Iс нас /Iс нас0= 1.
Рис. 35. К решению уравнения (2.26).
При очень малых токах стока температурный коэффициент Vзи приближается к dVнac/dT, равному примерно 2 мв/град.
В гл. 1 мы видели, что механизм пробоя полевого транзистора можно объяснить возникновением лавинного процесса в переходе затвор - канал. Мы видели также, что обратное напряжение диода затвор — канал изменяется вдоль длины затвора, достигая максимального значения у стокового конца канала. Именно здесь происходит пробой полевого транзистора, не имеющего технологических дефектов. Если выводы стока и истока поменять местами, то пробивное напряжение почти не изменится. Поскольку для уменьшения тока стока необходимо увеличить обратное напряжение в цепи исток — затвор, то при фиксированном напряжении питания сток — исток .кажущееся напряжение пробоя в области стока должно монотонно уменьшаться вместе с уменьшением тока. Рассмотрим характеристики, изображенные на рис. 30. Когда Vзи=0, пробой наступает при Vcи= -27 в (прибор с каналом р-типа). Вспомним теперь, что в действительности пробой происходит между областями стока и затвора; это значит, что в цепи затвора течет большой ток, и поскольку затвор имеет нулевой потенциал по отношению к истоку, то пробивное напряжение цепи транзистора.
Если теперь повысить напряжение Vзи на +0,2 в, то напряжение пробоя цепи затвор — сток остается, как и прежде, равным —27 в, но кажущееся напряжение пробоя цепи сток — исток будет равным —26,8 в. Предельным для прибора является пробивное напряжение цепи сток — затвор. Теоретически оно будет постоянным независимо от потенциала истока, который может изменяться от потенциала стока в. одном крайнем случае до потенциала затвора в другом. Обычно это напряжение определяется при разомкнутой цепи истока и в согласии с принятой системой обозначений ему соответствует символ BVC30. Если на исток подано некоторое напряжение смещения X в, то кажущееся напряжение пробоя цепи сток — исток, обозначаемое BVсиХ, будет связано с напряжением BVc30 следующим соотношением:
BVсиХ = BVc30+VзиХ. (2.27)
Затвор и канал в униполярном полевом транзисторе образуют р-n-переход; ток через этот переход и напряжение на нем подчиняются известному экспоненциальному соотношению:
(2.28)
где I3 — ток затвора; I30 — обратный ток затвора при насыщении; V3K — напряжение цепи затвор — канал (при прямом смещении положительное); k—постоянная Больцмана, дж/град; Т—абсолютная температура, °К.
Когда в качестве входного вывода полевого транзистора используется затвор, входная динамическая проводимость прибора определяется наклоном входной вольтамперной характеристики, изображенной на рис. 2.7; эта кривая представляет собой качественный график уравнения (2.28) для области, близкой к началу координат. Из уравнения (2.28) dI3/dV3K равно
(2.29)
Величина kT/q при комнатной температуре равна примерно 25 мв, а ток I30 униполярного полевого транзистора может быть равным всего 10-10 а. При I3=0 (Vзк = 0) входное сопротивление такого полевого транзистора при комнатной температуре может достигать 250 Мом и с увеличением обратного смещения будет повышаться. Поскольку полевой транзистор обычно работает при обратном смещении, на затворе, он, очевидно, представляет собой прибор с весьма высоким входным импедансом. Эквивалентная схема входной цепи полевого транзистора, находящегося при нормальном смещении, состоит из очень большого по величине нелинейного активного сопротивления, шунтированного конденсатором, номинальная емкость которого для реальных приборов лежит в пределах от 1 до 50 пф, и генератора очень слабого стабильного тока. Уравнение (2.29) показывает, что нелинейное входное сопротивление может стать весьма малым, если на затвор транзистора подать прямое смещение. Этим недостатком не обладают полевые транзисторы с поверхностным барьером.
4.6 Активное сопротивление открытого канала
Величина rс откр ,т. е. сопротивления цепи сток-сток при Vзи=0, равна тангенсу угла наклона кривой зависимости Vзи от Iс в начале координат при нулевом напряжении смещения. По определению, эта величина равна 1/gmмакс; вспомним, что gmмакс есть проводимость участка канала, имеющего форму параллелепипеда и ограниченного у истокового конца обедненными слоями. При измерении rс откр ток в канале отсутствует, и эффектами модуляции толщины канала можно пренебречь.
В общем случае сопротивление канала при нулевом напряжении стока и произвольном смещении равно rс = l/gm, следовательно, на основании (2.19) имеем
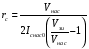 (2.30)
(2.30)
Это сопротивление можно снизить до величины, меньшей, чем rс откр, подав на затвор прямое смещение. Минимальная возможная величина rс равна
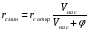 (2.31)
(2.31)
4.7 Работа прибора на низких частотах в режиме малого сигнала
Ток в канале полевого транзистора можно, по существу, рассматривать как ток в нелинейной резистивно-емкостной линии передачи с распределенными параметрами, однако при работе на низких частотах достаточно считать прибор нелинейной электрической цепью с сосредоточенными параметрами. Эквивалентная схема, содержащая все сосредоточенные элементы, необходимые для анализа работы прибора на низких частотах, представлена на рис. 36. Емкости Ссз и Сиз и проводимости gc3 и gиз замещают в этой схеме переход затвор-канал, находящийся под обратным смещением. В правильно сконструированном полевом транзисторе gc3 и gиз будут весьма малы, и их можно рассматривать как цепочки с бесконечно большим сопротивлением (paзомкнутые цепочки). Величины rс и rи представляют собой объемные сопротивления полупроводника на участках между концами канала и контактами стока и истока, соответственно. Эти сопротивления будут иметь величины порядка 100 ом или менее в зависимости от геометрии прибора и технологии его изготовления.
На низких частотах влиянием сопротивления rс вполне можно пренебречь и считать его малой частью сопротивления нагрузки, которое обычно достаточно велико. Сопротивление rи оказывает небольшое влияние на эффективную крутизну характеристики прибора, однако и этим влиянием обычно пренебрегают. Напряжение v'зи на рис. 36 связано с напряжением vзи на выводе прибора соотношением
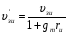 (2.32)
(2.32)
Для полевого транзистора, у которого gm= l ма/в, а rи=75 ом, знаменатель выражения (2.32) равен 1,075.
Величина gси представляет собой тангенс угла наклона выходной характеристики в области насыщения и обычно мала по сравнению с проводимостью нагрузки.
Рис. 37. Общая эквивалентная схема четырехполюсника для вычисления y-параметров полевого транзистора.
У изготовителей вошло в практику указывать в качестве технических данных полевого транзистора комплексные параметры проводимости его эквивалентной схемы в режиме короткого замыкания. Общая эквивалентная схема четырехполюсника для вычисления параметров представлена на рис. 37. Напряжения и токи на выводах прибора в режиме малого сигнала, вычисленные для схемы с общим истоком, соответствуют следующим характеристическим уравнениям четырехполюсника :
iз=yвх иvзи+yобр иvси (2.33)
iс=yпр иvзи+yвых иvси (2.34)
Условия для определения отдельных параметров следующие:
короткое замыкание на выходе
увх и=iз /vзи , упр и=ic/vзи
короткое замыкание на входе
уобр и=iз/vси , увых и=iс/vси
Если эти условия воспроизвести на эквивалентной схеме рис. 36, то y-параметры можно выразить через величины сосредоточенных элементов — сопротивлений, емкостей и э. д. с. Пренебрегая всеми проводимостями диодов и объемными сопротивлениями полупроводника, получим
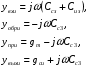 (2.35-2.38)
(2.35-2.38)
Все эти параметры зависят от смещения. Мы уже видели, что зависимость gm от смещения в области насыщения легко найти, дифференцируя квадратичное приближение для тока 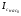 по vзи :
по vзи :
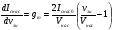 (2,39)
(2,39)
Если желательно выразить gm через Iс нас, а не через Vзи, то путем простых алгебраических преобразований найдем
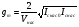 (2.40)
(2.40)
В гл. 1 мы установили, что получить аналитическое выражение для зависимости gси от смещения — безнадежная задача. Нам остается только полагаться на результаты измерений, сообщаемых поставщиком приборов,- или принять допущение, что проводимость нагрузки велика и проводимостью gси можно пренебречь.
Если можно ввести допущение, что суммарная емкость перехода канал — затвор равна (Ссз + Сиз), то ее можно выразить через постоянные полевого транзистора и характеристики, зависящие от смещения, которые связывают токи и напряжения на выводах прибора. Уравнение (1.44) мы записали в следующем виде:
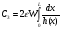
а уравнение (1.47) было записано в форме
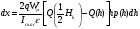
Подставляя выражение (1.47) в уравнение (1.44), получаем
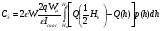 (2,41)
(2,41)
Теперь из уравнения (1.6) следует
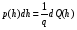 (2.42)
(2.42)
Подставляя это выражение в уравнение (2.41), имеем
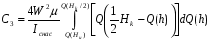 (2,43)
(2,43)
Уравнение (2.43) можно непосредственно проинтегрировать:
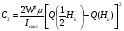 (2,44)
(2,44)
а это соотношение, пользуясь уравнением (1.25), можно переписать, введя gm:
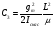 (2,45)
(2,45)
Величины L и — постоянные. Длина L для транзисторов, изготовляемых двойной диффузией, определяется размерами шаблона, используемого в фотолитографическом процессе; у полевых транзисторов типов 2N2497 и 2N3329 она равна приблизительно 0,013 мм. Величина (j,для дырок в кремнии р-типа равна 500 см2/в • сек. Уравнение (2.45) справедливо для полевого транзистора, имеющего идеальную геометрию. Полевой транзистор, изготовляемый при помощи двойной диффузии, имеет нижний затвор, или затвор-подложку большой площади, ввиду чего полная емкость затвора будет несколько больше рассчитанной. В будущем метод вывода контактных площадок на окисную пленку даст возможность в значительной степени уменьшить площадь нижнего затвора, а следовательно, обеспечить емкость затвора, более согласующуюся с расчетами, сделанными для идеальной модели. С целью дальнейших упрощений было бы соблазнительно использовать квадратичные приближения для h нас и gm в уравнении (2.45). Это сделать можно, но только надо с большой осторожностью толковать получаемые результаты. Вспомним, что квадратичное приближение является достаточно точным лишь для тех приборов, у которых толщина канала мала по сравнению € толщиной обедненного слоя, обусловленного контактной разностью потенциалов. Оно вполне точно для того предельного случая, когда канал имеет бесконечно малую толщину, т. е. для рассмотренного нами в гл. 1 распределения примесей, имеющего пик. Следовательно, мы должны ожидать, что если ввести квадратичное приближение в уравнение (2.45), то емкость затвор-канал не будет изменяться в зависимости от смещения.
Чтобы установить зависимость С3 от смещения, необходимо оценить величину gm и 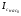 по приведенным в гл.. 1 данным о геометрии прибора и распределении в нем примесей. Мы используем здесь квадратичное приближение потому, что оно позволяет весьма быстро произвести оценку частотных свойств тех полевых транзисторов, о которых изготовитель в каталоге приводит только данные, относящиеся к статическим характеристикам. В настоящее время еще распространено несколько каталогов такого типа, однако все они, в конце концов, будут вытеснены новой регистрационной формой, введенной Ассоциацией электронной промышленности.
по приведенным в гл.. 1 данным о геометрии прибора и распределении в нем примесей. Мы используем здесь квадратичное приближение потому, что оно позволяет весьма быстро произвести оценку частотных свойств тех полевых транзисторов, о которых изготовитель в каталоге приводит только данные, относящиеся к статическим характеристикам. В настоящее время еще распространено несколько каталогов такого типа, однако все они, в конце концов, будут вытеснены новой регистрационной формой, введенной Ассоциацией электронной промышленности.
Подставляя квадратичные приближения для gm и 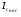 в уравнение (2.45), получаем
в уравнение (2.45), получаем
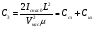 (2,46)
(2,46)
4.8 Эффекты второго порядка на высоких частотах
Изображенные на схеме рис. 36 объемные сопротивления rс и rи приводят к появлению членов второго порядка в приолиженных уравнениях (2.35) —(2.38) для y-параметров полевого транзистора. Причины этого объясняет простой пример, показанный на рис. 38. Фундаментальная теорема из курса теории электрических цепей утверждает, что любую последовательную схему, например схему рис. 38а, можно для фиксированной частоты заменить некоторой параллельной схемой, например схемой, изображенной на рис. 38,б.
Рис 38 Последовательное (а, и параллельное (б) соединение конденсатора и резистора.
На любой частоте
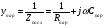 (2-47)
(2-47)
Где
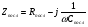
Подставляя эти комплексные величины вместо упар и Zпосл в уравнение (2.47) и приравнивая попарно действительные и мнимые члены, получаем
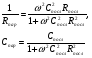 (2.48-2.49)
(2.48-2.49)
На частотах, при которых 2C2послR2посл1, упар можно приблизительно представить выражением
упар = (2С2посл Rпосл +jCпосл (2.50)
Таким образом, действительная часть, содержащая квадрат частоты, является членом второго порядка, а мнимая часть представляет собой член первого порядка, зависящий от первой степени угловой частоты. Если учесть в выражениях для у-параметров влияние сопротивлений rс и rи (рис. 36) и принять подходящие упрощающие допущения, то выражения для увхи, уобр и и увыхи с учетом эффектов второго порядка можно практически сразу переписать в следующем виде:
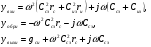 (2,51-2,53)
(2,51-2,53)
Эти приближенные выражения очень хорошо объясняют характер изменения у-параметров на высоких частотах, не слишком усложняя модель прибора. На рис. 2.11—2.13 приведены зависимости этих у-параметров от частоты для транзистора типа 2N2499. Отметим, что наклон кривой, представляющей мнимую часть каждого из трех предыдущих уравнений, равен примерно 20 дб на декаду, а действительные части имеют наклон около 40 дб на декаду, что объясняется наличием в соответствующих выражениях членов, содержащих 1-ю и 2-ю степени частоты. Численные значения величин приведенных на графиках, можно проверить, пользуясь техническими данными, представленными изготовителем полевого транзистора 2N2499: сопротивления rс и rи у этого прибора равны каждое примерно 50 ом.
В полевом транзисторе действуют три основных вида шумов:
1. Полный дробовой шум, вызываемый током утечки затвора.
2. Напряжение теплового шума, генерируемое в проводящем канале и модулирующее толщину обедненного слоя.
3. Шум генерации-рекомбинации в обедненном слое; величина этого шума обратно пропорциональна частоте, и он также модулирует толщину обедненного слоя.
Ток дробового шума, обусловленный случайными изменениями плотности носителей, собираемых по обе стороны перехода, определяется выражением
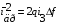 (2.54)
(2.54)
где i3 — прямой или обратный ток затвора; q — заряд электрона, равный 1,6019- 10-19 к и  f — эффективная ширина полосы шумов, гц. В униполярном полевом транзисторе, который обычно работает при обратном смещении на затворе, обратный ток перехода может изменяться от 10~8 до 10-10 а. В приборе с поверхностным барьером ток i3 очень мал, порядка 10-15 а или менее, так что этим источником шума можно пренебречь, так как он не является определяющим.
f — эффективная ширина полосы шумов, гц. В униполярном полевом транзисторе, который обычно работает при обратном смещении на затворе, обратный ток перехода может изменяться от 10~8 до 10-10 а. В приборе с поверхностным барьером ток i3 очень мал, порядка 10-15 а или менее, так что этим источником шума можно пренебречь, так как он не является определяющим.
Как показал Ван дер Зил [2.2], тепловой шум, генерируемый в проводящем канале, приблизительно эквивалентен шуму, 'создаваемому внешним сопротивлением в цепи истока, равным l/gm . Напряжение теплового шума в таком резисторе дается выражением
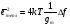 (2.55)
(2.55)
Генерационно-рекомбинационный шум в обедненном слое существенно изменяет выражение (2.55) для напряжения теплового шума; чтобы учесть его, надо в предыдущее уравнение ввести член, зависящий от 1/f:
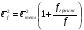 (2.56)
(2.56)
где fгрнижн — частота нижней границы полосы. Эти физические механизмы позволяют охарактеризовать полевой транзистор так называемым двухгенераторным методом. Основная теорема этого метода гласит, что любой активный линейный четырехполюсник можно представить последовательным генератором напряжения шума и параллельным генератором шумового тока, присоединенными к входу идеального четырехполюсника, не содержащего источников шумов. Данный способ исследования шумовых свойств годится только для случая малого сигнала, однако поскольку шумовые сигналы обычно слабы, никаких трудностей здесь не возникает. Величина представляет собой коэффициент корреляции между двумя источниками шумов, с помощью которого учитывается наличие или отсутствие влияния этих источников друг на друга. Если равно 1, между выходами обоих генераторов имеется функциональная связь. Если же равно нулю, генераторы совершенно не зависят один от другого.
К счастью, в полевом транзисторе имеет место слабая корреляция между дробовым шумом, обусловленным током утечки затвора, и тепловым шумом в канале. Величины еш и iш можно измерить непосредственно, однако измерение iш осуществить очень трудно. Для измерения е вывод затвора . полевого транзистора соединяют с истоком через малое сопротивление, предпочтительно через короткозамыкающую перемычку, удовлетворяющую следующим условиям:
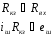
Первое условие гарантирует, что все напряжение шума еш будет приложено ко входу усилителя, второе ограничивает величину тока сигнала, обусловленного источником iш. Выходной ток полевого транзистора содержит шумовую компоненту, которая представляет собой произведение эффективного напряжения теплового шума, генерируемого в канале и обедненном слое, на величину gm- Следовательно, чтобы найти еш, надо просто поделить результат измерения на gm:
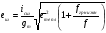 (2-57)
(2-57)
Известно, что у полевого транзистора 2N2500 величина fгрнижн равна 32 кгц. Наличие этих данных позволяет с помощью уравнения (2.57) достаточно точно определять эквивалентное входное напряжение шума этого и, вообще говоря, большинства других полевых транзисторов, изготовляемых двойной диффузией. Не следует только путать величину fгрнижн с граничной частотой коэффициента шума.
При измерении iш необходимо разомкнуть входную цепь транзистора настолько, чтобы сопротивление Rразомкн при этом удовлетворяло следующим условиям:
Rразомкн>Rвх
iшRразомкн>eш
Первое требование выполнить чрезвычайно трудно. В большинстве случаев достаточно измерить ток утечки затвора при желаемом смещении и вычислить iш, используя уравнение (2.54), где iш=(i2др)1/2, а i3 = IзиХ, т. е. равно статическому току затвора при наличии смещения.
Глава 5 Приборы с зарядовой связью
Рис.41. Структура ПЗС
Прибор с зарядовой связью (ПЗС) представляет собой ряд простых МДП-структур (металл — диэлектрик— полупроводник), сформированные на общей полупроводниковой подложке таким образом, что полоски металлических электродов образуют линейную или матричную регулярную систему, в которой расстояния между соседними электродами достаточно малы (рис.41). Это обстоятельство обусловливает тот факт, что в работе устройства определяющим является взаимовлияние соседних МДП-структур [1—3].
Принцип действия ПЗС заключается в следующем. Если к любому металлическому электроду ПЗС приложить отрицательное напряжение, то под действием возникающего электрического поля электроны, являющиеся основными носителями в подложке, уходят от поверхности в глубь полупроводника. У поверхности же образуется обедненная область, которая на энергетической диаграмме представляет собой потенциальную яму для неосновных носителей — дырок. Попадающие каким-либо образом в эту область дырки притягиваются к границе раздела диэлектрик — полупроводник и локализуются в узком приповерхностном слое.
Если теперь к соседнему электроду приложить отрицательное напряжение большей амплитуды, то образуется более глубокая потенциальная яма и дырки переходят в нее. Прикладывая к различным электродам ПЗС необходимые управляющие напряжения, можно обеспечить как хранение зарядов в тех или иных приповерхностных областях, так и направленное перемещение зарядов вдоль поверхности (от структуры к структуре). Введение зарядового пакета (запись) может осуществляться либо p-n-переходом, расположенным, например, вблизи крайнего ПЗС элемента (электрод 1 на рис.41), либо светогенерацией. Вывод заряда из системы (считывание) проще всего также осуществить с помощью p-n-перехода (электрод п на рис.41.). Таким образом, ПЗС представляет собой устройство, в котором внешняя информация (электрические или световые сигналы) преобразуется в зарядовые пакеты подвижных носителей, определенным образом размещаемые в приповерхностных областях, а обработка информации осуществляется управляемым перемещением этих пакетов вдоль поверхности. Очевидно, что на основе ПЗС можно строить цифровые и аналоговые системы. Для цифровых систем важен лишь факт наличия или отсутствия заряда дырок в том или ином элементе ПЗС, при аналоговой обработке имеют дело с величинами перемещающихся зарядов.
Естественно, что заряд, введенный в МДП-структуру, не может храниться в ней неограниченно долго. Процесс термогенерации электронно-дырочных пар в объеме полупроводника и на границе раздела диэлектрик — полупроводник ведет к накоплению в потенциальных ямах паразитных зарядов и, следовательно, к искажению зарядовой информации, а с течением времени и к полному ее «стиранию». Это время может достигать сотен миллисекунд и даже десятков секунд, но, тем не менее, оно конечно и определяет существование нижней граничной частоты. Таким образом, работа прибора основана на нестационарном состоянии МДП-структуры, и ПЗС являются элементами динамического типа.
Устройство и физика работы ПЗС определяют целый ряд очень интересных и полезных (а нередко и уникальных) особенностей этих приборов.
К числу важнейших функциональных особенностей ПЗС относятся возможность хранения, зарядовой информации; возможность направленной передачи зарядов вдоль поверхности полупроводникового кристалла; возможность преобразования светового потока в электрический заряд и последующего его считывания (сканирования). Достоинством ПЗС является малая потребляемая мощность (5—10 мкВт/бит в режиме передачи информации и практически полное отсутствие затрат энергии в режиме хранения), что обусловлено МДП-структурой этих устройств. Простота конфигурации и регулярность системы элементов в ПЗС ведет к тому, что быстродействие этих приборов может быть очень высоким (у специально сконструированных образцов предельные тактовые частоты лежат в гигагерцевом диапазоне) [14].
Пожалуй, еще более важными являются конструктивно-технологические достоинства ПЗС, основными из которых являются технологическая ясность и простота (малое число фотолитографических, термодиффузионных и эпитаксиальных процессов при изготовлении прибора) — обязательное условие при создании качественных многоэлементных (с числом элементов 104—106) устройств; высокая степень интеграции (превышающая 105 элементов на одном кристалле) и высокая плотность упаковки (более 105 бит/см2); малое количество внешних выводов, что является определяющим при построении высоконадежных систем; отсутствие p-n-переходов (немногочисленные p-n-переходы ПЗС выполняют «подсобные» функции и к ним предъявляются достаточно «слабые» требования), что, в частности, открывает широкие возможности для использования наряду с кремнием других полупроводниковых материалов (например, арсенида галлия).[14]
Все эти свойства открывают широкие перспективы для разнообразных применений ПЗС.
Для цифровой техники интересны сдвиговые регистры, оперативные запоминающие устройства, логические схемы. Линии задержки аналоговых сигналов на ПЗС по техническим характеристикам значительно превосходят свои акустические и магнитные аналоги.[6,7]
В оптоэлектронной технике преобразования изображений ПЗС открывают принципиальные новые возможности для создания безвакуумных полупроводниковых формирователей видеосигналов. Присущее им самосканирование позволяет избавиться от громоздких и ненадежных высоковольтных вакуумных трубок со сканированием электронным лучом. ПЗС являются уникальными аналогами ЭЛТ, позволяющими одновременно с уменьшением массы, габаритных размеров, потребляемой мощности повысить надежность и качество формирователей видеосигналов. Дополнительное достоинство фотоприемников на основе ПЗС заключается в принципиальной возможности использовать разнообразные полупроводниковые материалы, что позволит перекрыть широкую область электромагнитного спектра (включая и ИК-область).[6]
Создание передающих телевизионных камер на основе ПЗС приведет в будущем не только к оснащению техники надежным «электронным глазом» (отметим, что в проекте создания средств искусственного зрения для человека ориентация делается также на ПЗС), но и к действительно широкому использованию средств телевидения в быту.
Если на многоэлементный или матричный ПЗС направить световой поток, несущий изображение, то в объеме полупроводника начнется фотогенерация электронно-дырочных пар. Попадая в обедненную область ПЗС, носители разделяются и в потенциальных ямах накапливаются дырки (причем величина накапливаемого заряда пропорциональна локальной освещенности). По истечении некоторого времени (порядка нескольких миллисекунд), достаточного для восприятия изображения, в матрице ПЗС будет храниться картина зарядовых пакетов, соответствующая распределению освещенностей. При включении тактовых импульсов зарядовые пакеты будут перемещаться к выходному устройству считывания, преобразующему их в электрические сигналы. В результате на выходе получится последовательность импульсов с разной амплитудой, огибающая, которых дает видеосигнал.
На этой основе создаются, учитывающие устройства для фототелеграфа, а также, передающие камеры (вплоть до камер полноформатного цветного телевидения). В будущем ПЗС найдут применение в качестве удобных матричных фотоприемников в сверхпроизводительных оптоэлектронных вычислительных машинах с параллельной обработкой информации.
Появление ПЗС (1969 г.) явилось результатом исследований в области физики и технологии МДП-приборов[13]. Разработка этого нового направления полупроводниковой техники занимаются многие научные коллективы в разных странах мира и уже достигнуты весьма заметные результаты.
Созданы быстродействующие однокристальные ЗУ на ПЗС емкостью 8192, 16384 и 65536 бит с временем выборки 64—200 мкс и скоростью выдачи информации 1—5 МГц; на базе кристаллов емкостью 16 К (килобит) сконструировано ЗУ емкостью 1 Мбит с блочной выборкой по 256 бит. Разработана широкополосная линия задержки аналоговых сигналов емкостью 128 разрядов, предназначенная для использования в системах цветного телевидения; опробован коррелятор на ПЗС, позволяющий одновременно обрабатывать 40 000 дискретных значений сигнала с общей погрешностью менее 1%.[6]
Имеются многочисленные сообщения о начале промышленного выпуска рядом фирм США (в первую очередь Bell и RCA) передающих телекамер с числом элементов разложения 200X200 и 500x500. [13]
В то же время нельзя не заметить, что на пути широкого использования ПЗС стоит еще много нерешенных проблем — и в первую очередь технологическая: проколы диэлектрической пленки и закоротки электродных шин все еще не позволяют уверенно с высоким процентом выхода получать бездефектные ПЗС достаточно большой информационной емкости. Важнейшей технологической проблемой создания больших ПЗС с однослойной металлизацией является проблема получения узких (2—3 мкм) зазоров между электродами; основной технологический брак в таких структурах — закоротки. В структурах с многослойными кремниевыми затворами трудно получить высококачественный изолирующий диэлектрик между всеми уровнями поликремния.
В заключение хотелось бы отметить, что создание устройств на приборах с зарядовой связью, в особенности оптоэлектронных, является важным этапом в развитии больших интегральных схем и одним из первых реальных шагов по пути к функциональной микроэлектронике[16].
5.1 Физические основы работы и конструкции приборов с зарядовой связью
Динамику перемещения зарядовых пакетов в ПЗС проследим на примере трехкратного сдвигового регистра (рис.42).
В этой схеме каждый третий электрод подключается к соответствующей шине тактовых импульсов. В исходном состоянии (рис.42,а) под напряжением хранения
Uхр. =-U2 находятся электроды 1, 4, 7, а все остальные — под напряжением – U1 (U1<U2); подложка заземлена. Напряжение U1 выбирается немного большим порогового напряжения U0 (величина U0 для МДП-структуры определяется как
минимальное напряжение на затворе, при котором наступает инверсия поверхности полупроводника) для того, чтобы вся ^поверхность полупроводника была обеднена и на поверхностных состояниях отсутствовали электроны. Допустим, что в потенциальных ямах 1, 7 есть зарядовые пакеты, а в 4 их нет. На следующем такте к электродам 2, 5, 8 прикладывается напряжение записи Uзап. = -U3(U3>U2) и заряды перетекают от ПЗС1 (строго говоря, в данном случае следует использовать термин «ПЗС-элемент» или «МДП-структура», так как речь идет об одном элементе прибора с зарядовой связью. Однако для сокращения здесь и в дальнейшем (если из контекста ясно, что речь идет об элементе) используется термин «ПЗС», а слово «элемент» опускается.) к ПЗС2 и от ПЗС7 к ПЗС8 (рис.43,б).
На следующем такте на электродах устанавливаются напряжения и начинается фаза хранения зарядовой информации в элементах 2, 5, 8.
Таким образом, для ПЗС характерны два режима работы: хранение и передача зарядовых пакетов. В режиме хранения ПЗС эквивалентен МДП-емкости. Зонная диаграмма поверхности полупроводника для режима хранения приведена на рис.35,а. Величина поверхностного потенциала, характеризующая изгиб зон и глубину потенциальной ямы, в начальный момент максимальна. При инжекции пакета дырок их положительный заряд экранирует подложку от поля, в результате чего происходит перераспределение внешнего напряжения: увеличивается часть напряжения, падающего на слое диэлектрика, поверхностный потенциал уменьшается (по абсолютной величине), и обедненная область сужается. С течением времени потенциальная яма заполняется до насыщения термогенерируемыми дырками и у поверхности образуется стационарный инверсный слой (рис.35,б). Величина поверхностного потенциала уменьшается (по абсолютной величине) до потенциала инверсии поверхности полупроводника φ0
В нестационарном состоянии поверхностный потенциал φ зависит от напряжения на затворе U3, плотности (на единицу поверхности) заряда дырок Qp и от электрофизических характеристик диэлектрической пленки и подложки:
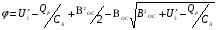 (54)
(54)
где U'3 = U3 - UП3 = U3 - Uo - φ0 + UВ - напряжение плоских зон; 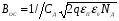 - коэффициент подложки; UB = BOC
- коэффициент подложки; UB = BOC 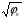 ; Сд = εдε0хд - удельная емкость диэлектрика затвора толщиной хд . В (1) и последующих выражениях используются абсолютные значения потенциалов и зарядов, что делает их применимыми для р- и n-канальных ПЗС.
; Сд = εдε0хд - удельная емкость диэлектрика затвора толщиной хд . В (1) и последующих выражениях используются абсолютные значения потенциалов и зарядов, что делает их применимыми для р- и n-канальных ПЗС.
Зависимости φ(QP) для разные значений напряжений затвора приведены на рис.44.
При увеличении заряда дырок Qp от нуля до стационарного значения поверхностный потенциал уменьшается по абсолютной величине до потенциала инверсии φ0. Из графиков рис.44 видно, что зависимости φ(QP) практически линейны. Аппроксимированное выражение для φ имеет вид:
φ=(U'3-QP/Cд)(1+x), (55)
где х=0,1—0,2 — линеаризованный коэффициент подложки.
Максимальный заряд QPM, который может быть помещен в потенциальную яму при заданном напряжении U3, определяется из (56) при условии насыщения потенциальной ямы, т. е. при φ=φ0,
QPM = Сд (U3, — U0) (56)
Обычно QPM= (1—5) 10-3 пКл/мкм2.
Наглядным представлением потенциальной ямы ПЗС может служить прямоугольный сосуд с жидкостью. Максимальная глубина потенциальной ямы соответствует высоте пустого сосуда; но мере заполнения сосуда жидкостью его эффективная глубина уменьшается. Допустимое время хранения заряда определяется процессами, приводящими к накоплению паразитного заряда QP. В основном это термогенерация электронно-дырочных пар в обедненном слое и на поверхности, а также до некоторой степени диффузия неосновных носителей из объемной нейтральной области.
Расчет показывает, что при малых значениях накапливаемого паразитного заряда QP его зависимость от времени близка к линейной, в дальнейшем кривые становятся сублинейными, приближаясь к постоянному значению QPM, определяемому соотношением (56).
На рис.44 приведены расчетные кривые для U3 = 10 В, Nд=5·1014 см-3, U0=3,8 В, тепловая скорость υт=107 см/с, сечение захвата σv = 2,2-10-16 см2, плотность объемных центров Nоб=l,8·1014 см-3, плотность поверхностных центров Nпов=6·1010 см-2. При этих параметрах и при QP = 0 время накопления паразитного заряда, составляющего 1 % от QpM, равно 20 мс (для многоэлементных ПЗС, и в особенности для аналоговых устройств, большее накопление паразитного заряда недопустимо).[6]
Максимальное время хранения можно определить и экспериментально, измерив время релаксации МДП-емкости, сформированной в тех же условиях, что и ПЗС, и включаемой таким же импульсом напряжения. Приближенно время накопления паразитного заряда, равного по величине информационному, на порядок меньше времени релаксации МДП-емкости. Опыт показывает, что в зависимости от качества обработки поверхности кремния и совершенства структуры подложки время релаксации лежит в пределах 1—60 с и соответственно время накопления паразитного заряда составляет 0,1— 6 с. Задаваясь требуемым соотношением между величинами информационного и паразитного зарядов, нетрудно рассчитать максимальное время хранения информации в ПЗС. При соотношении 100: 1 это время составляет десятки миллисекунд.
Рис.46.Схема передачи заряда в ПЗС
Еще раз отметим, что процессы накопления паразитного заряда определяют максимальное время хранения и минимальную частоту работы цифровых и аналоговые устройств на ПЗС, а также темновые токи в фотоприемных ПЗС. Передача заряда из элемента в элемент осуществляется приложением к соседнему электроду большего по амплитуде напряжения записи Uзап (рис.46). В зазоре между электродами (обозначим его длину через l) возникает тянущее поле, под действием которого дырки перетекают в более глубокую потенциальную яму.
По мере перетекания зарядов поверхностный потенциал в ПЗС1 увеличивается (по абсолютной величине), а в ПЗС2 уменьшается, в результате чего поле в зазоре уменьшается.
Очевидно, что напряжение записи Uзап должно превышать напряжение хранения Uхр тем значительнее, чем больше расстояние между электродами и чем сильнее легирована кремниевая подложка (рис.38). Из рисунка видно, что практически для работоспособных ПЗС ширина зазора не должна превышать l = 2-3 мкм, a Nд≤1015 см-3. Минимальная амплитуда импульса записи Uзап линейно увеличивается при возрастании UXP и QP.
Рассмотрим динамику переноса заряда из одного элемента (ПЗС1) в другой (ПЗС2) (рис.45). В режиме хранения к ПЗС1 приложен потенциал UXP, к ПЗС2 - нулевой потенциал. Заряд дырок плотностью Qp равномерно локализован в ПЗС1. После приложения к ПЗС2 потенциала записи Uзап>Uхр в зазоре между ячейками устанавливается тянущее поле, причем обычно напряженность его столь высока, что дырки, находящиеся вблизи левой границы ПЗС1, практически мгновенно переходят в ПЗС2. Концентрация дырок вблизи правой границы ПЗС2 очень быстро спадает до нуля (т. е. поле зазора действует аналогично полю обратного смещенного коллекторного p-n-перехода в транзисторе). Резкое изменение равномерности распределения дырок в ПЗС1 вызывает их интенсивный дрейф и диффузию внутри потенциальной ямы слева на право.
Если положить l<<L и рассматривать одномерный случай, то, как обычно при таких процессах, для времени передачи заряда приближенно должно выполняться:
tпер ~ L2/μpэ (57)
где L — длина затворов (электродов) ПЗС;
μрэ—поверхностная эффективная подвижность.
Очевидно, что коэффициент пропорциональности в (57) зависит от того, какой коэффициент эффективности передачи  требуется получить. Обычно для многоэлементных ПЗС этот уровень очень высок и составляет
требуется получить. Обычно для многоэлементных ПЗС этот уровень очень высок и составляет
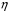 = QРППЗС2/ QРП ПЗС1 = 0,99-0,9999, (58)
= QРППЗС2/ QРП ПЗС1 = 0,99-0,9999, (58)
где QPП — полный заряд в одной ячейке.
По мере перетекания заряда из ПЗС1 в ПЗО2 концентрация дырок в ПЗС1, а следовательно, и дрейфовая составляющая тока уменьшаются и процесс передачи, определяемый только диффузией, замедляется -«хвост» переходного процесса всегда более затянут по сравнению с начальной фазой (рис.48). Чем больше начальная плотность заряда Qp, тем большая его часть «вытечет» за время первой быстрой стадии и тем меньше (при заданном допустимом значении 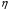 ) будет время передачи tпер. Эпюры распределения плотности Заряда дырок в различные моменты времени представлены на рис.49. Через левую границу ПЗС1 потока дырок нет, поэтому на графиках рис.46 в любой момент времени градиент концентрации дырок в этой точке равен нулю.
) будет время передачи tпер. Эпюры распределения плотности Заряда дырок в различные моменты времени представлены на рис.49. Через левую границу ПЗС1 потока дырок нет, поэтому на графиках рис.46 в любой момент времени градиент концентрации дырок в этой точке равен нулю.
Наглядной аналогией процесса передачи заряда является вытекание вязкой жидкости из прямоугольного сосуда, торцевая стенка которого (соответствующая правой границе потенциальной ямы ПЗС) отодвинута так же, как и в ПЗС, чем больше начальный уровень жидкости, тем быстрее выльется заданная ее часть.
Для большинства реальных структур ПЗС размеры L и l соизмеримы и очень малы; при этих условиях; становится существенным эффект проникновения краевого поля Еkр (которое мы выше считали полностью сосредоточенным в зазоре) в область ПЗС1, что оказывает определяющее влияние на перетекание оставшейся части зарядового пакета.
Рассмотрим важнейшую характеристику ПЗС — эффективность передачи заряда 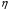 , представляющую собой часть заряда дырок, перешедшую из ПЗС1 в ПЗС2 за время передачи. При заданном допустимом уменьшении ^зарядового пакета значение
, представляющую собой часть заряда дырок, перешедшую из ПЗС1 в ПЗС2 за время передачи. При заданном допустимом уменьшении ^зарядового пакета значение 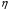 определяет максимальное количество элементов, через которое информация может быть передана без восстановления. Часто оказывается удобнее использовать понятие потери (неэффективности) передачи ε =1—
определяет максимальное количество элементов, через которое информация может быть передана без восстановления. Часто оказывается удобнее использовать понятие потери (неэффективности) передачи ε =1—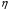 . При конечном времени передачи потери заряда обусловлены, во-первых, тем, что за t=tnep часть заряда ε1 просто не успевает перетечь в соседнюю ячейку и, во-вторых, захватом части носителей ε2 поверхностными ловушками. Составляющая ε1 определяет потери передачи на высоких частотах, ε2—на низких и средних частотах работы[6,7].
. При конечном времени передачи потери заряда обусловлены, во-первых, тем, что за t=tnep часть заряда ε1 просто не успевает перетечь в соседнюю ячейку и, во-вторых, захватом части носителей ε2 поверхностными ловушками. Составляющая ε1 определяет потери передачи на высоких частотах, ε2—на низких и средних частотах работы[6,7].
Рассмотрим подробнее захват носителей поверхностными ловушками. Если, например, в ПЗС1 поступает информационный пакет, то часть дырок захватывается
границей раздела диэлектрик — полупроводник. На следующем такте зарядовый пакет перетекает в ПЗС2, равновесие между инверсным слоем и поверхностными ловушками нарушается, и они начинают разряжаться. Те носители, которые освобождаются ловушками за t=tnep, успевают вернуться в зарядовый пакет, остальные образуют потери передачи ε2 . Потери ε2зависят не только от плотности поверхностных ловушек и величины зарядового пакета, но и от характера предшествующей зарядовой информации, передаваемой через данный элемент. Если передается серия логических 1 (которой соответствуют большие зарядовые пакеты), то потери ε2 будут максимальны в первом зарядовом пакете и будут уменьшаться в последующих, так как часть ловушек, захвативших заряды от первого пакета, не успеет разрядиться к приходу следующего и эти ловушки не будут участвовать в захвате носителей. Наихудшим случаем с точки зрения потерь ε2 является передача чередующейся последовательности логических 1 и 0. В этом случае выражение для ε2 имеет вид:
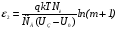 (59)
(59)
где Nл — плотность поверхностных ловушек; т = 2, 3 ... — количество управляющих тактов; Сд(U3—U0) — величина зарядового пакета. В типичных структурах ε2=(2—3) 10-3 и в первом приближении не зависит от тактовой частоты.
Влияние поверхностных состояний может быть уменьшено, если в цепочку ПЗС (в каждый зарядовый пакет) ввести некоторый фоновый заряд, заполняющий поверхностные ловушки. В результате потери информационного заряда при передаче уменьшаются. Неполное устранение влияния ловушек объясняется рядом причин, главными из которых являются краевой эффект и захват носителей не только при хранении, но и во время протекания зарядового пакета через ПЗС и зазор.
Краевой эффект возникает из-за двумерности распределения электрического поля в реальных ПЗС, что делает потенциальные ямы не прямоугольными, а закругленными. Следовательно, площадь поверхности занимаемая пакетом, будет зависеть от величины заряда и всегда будет больше площади, занимаемой меньшим по величине фоновым зарядом. Поэтому поверх постные ловушки, расположенные у краев электрода, где фонового заряда нет, будут пустыми и смогут захватывать носители из зарядного пакета. Потери заряда or этого эффекта составляют (4-5)10-4.
Захват носителей в процессе передачи главным образом связан с тем, что в зазоре фонового заряда нет и поэтому ловушки не заполнены. Обусловленная этим неэффективность составляет (2—3) 10-4. Таким образом, введение фонового заряда не позволяет выполнить условие ε2→0, но в несколько раз уменьшает потери передачи, обусловленные захватом носителей поверхностными ловушками.
В заключение рассмотрим фоточувствительность ПЗС. Одним из факторов, определяющих фоточувствительность, является коэффициент поглощения , который характеризует интенсивность поглощения фотонов (с образованием электронно-дырочных пар). Коэффициент поглощения резко уменьшается при увеличении длины волны падающего света. Поэтому область длин волн, в которой осуществляется эффективное преобразование светового потока в информационные заряды (называемая областью спектральной чувствительности) ограничена. Длинноволновая граница определяется шириной запрещенной зоны полупроводника и для кремния составляет 1,1 мкм. Коротковолновая граница составляет 0,4—0,5 мкм и обусловлена сильным поглощением коротковолновых квантов света в узком приповерхностном слое, в котором интенсивно происходит рекомбинация фотогенерируемых носителей.
Если считать, что все возбужденные носители собираются ПЗС, то зарядный пакет Qpn, накапливаемый за время генерации (интегрирования) ta под действием светового потока Нш, может быть рассчитан по следующему приближенному выражению:
QPП = qHизθtи·Aэ , (60)
где θ — квантовый выход; Аэ — часть площади элемента, воспринимающая свет. Для ПЗС θ=1, этому соответствует фоточувствительность порядка 500 мкА/лм. Пороговая чувствительность, при которой сигнал превышает шумы примерно в 2 раза, составляет для ПЗС около 10-4 лк·с. Фотоприемное устройство на ПЗС можно освещать со стороны затворов (электродов) или с обратном стоны[6].
Глава 6 Экспериментальная часть
6.1 Стоко-затворные характеристики полевого транзистора КП303Г и его температурная зависимость
В работе исследуется транзистор КП303 с каналом n-типа. На боковую поверхность канала нанесены слои полупроводника электронной электропроводности – затвор 2. Между затвором 3 и каналом образуется р-n-переход, обедненный слой которого сосредоточен главным образом в объеме канала, выполняемого из материала с низким содержанием примеси. От канала сделаны выводы 3 и 4 – сток и исток. Исток И обычно заземляют, а на сток С подают напряжение, при котором основные носители заряда устремляются к нему (рисунок 51).
В транзисторе с каналом n-типа на сток подается положительное напряжение, а на затвор – напряжение, при котором переход затвор-канал закрыт, и тока не проводит.
Выходной ток полевого транзистора – ток стока IС зависит от напряжения на стоке UСИ и с его ростом увеличивается. Кроме того, ток стока IС зависит от напряжения на затворе UЗ-И, которое управляет глубиной проникновения обедненного слоя 5 в объем канала, а, следовательно, его поперечным сечением.
При напряжении UСИ = 0 напряжение UЗИ вызывает уменьшение поперечного сечения канала (рис. 51 а) и увеличение его сопротивления. Появление напряжения UСИ изменяет конфигурацию обедненного слоя, причем сечение канала с приближением к стоку уменьшается, поскольку увеличивается разность потенциалов между затвором и каналом. При некотором напряжении UСИ, определенном для каждого значения напряжения UЗИ, обедненный слой смыкаются (точка А на рис.51 б) и наступает насыщение. Напряжение UСИ = UСИ нас. называют напряжением насыщения. При UЗИ=0 напряжение насыщения максимально.
Рисунок 51.
Рисунок 52.
Рисунок 53.
Увеличение напряжения UСИ приводит к смещению точки А в направлении истока (рис 52,в). Ток IC поддерживается за счет впрыскивания основных носителей канала в обедненную область точно так же, как в коллекторном переходе биполярного транзистора. При дальнейшем увеличении напряжения UCИ происходит пробой и выход транзистора из строя.
Стоко-затворная характеристика полевого транзистора (рис.53 а), снимаемая при постоянном напряжении UСИ, позволяет определить напряжение отсечки UЗИ отс, при котором ток стока становится равным нулю, и начальный ток стока IС нач, протекающий через канал при UЗИ=0.
Таким образом, выходной ток полевых транзисторов в отличие от биполярных транзисторов определяется напряжением на затворе UЗИ, при этом ток затвора близок к нулю, поскольку это обратный ток p-n- перехода. Аналитически стоко-затворная характеристика выражается уравнением
IC=f(UЗИ) при UСИ=const. (61)
На рисунке (52 б) показано семейство стоковых характеристик полевого транзистора, представляющих собой ряд зависимостей тока стока IС от напряжения между стоком и истоком UСИ для ряда постоянных напряжений на затворе UЗИ:
IС=f(UСИ) при UЗИ = const. (62)
Основными параметрами полевого транзистора являются крутизна стоко-затворной характеристики S и активная выходная проводимость g22И.
Крутизна S показывает, на сколько миллиампер изменится ток стока IС при изменении напряжения на затворе UЗИ а 1В и постоянном напряжении между стоком и истоком UСИ, т.е.
S = ΔIC/ΔUЗИ при UСИ= const (63)
Этим параметром определяются усилительные свойства прибора. Обычно крутизну измеряют или рассчитывают для режима, соответствующего линейному участку стоко-затворной характеристики. Для этого строят треугольник АВС (рис 52 а), по которому находят приращение тока ΔIC и напряжения ΔUЗИ, и по формуле (63) рассчитывают крутизну S.
При изучении температурной зависимости основных параметров полевого транзистора часть установки, показанную на рисунке 53, а именно полевой транзистор КП303Г, помещали в муфельную печь. Затем, меняя температуру в печи, проводили измерения статических характеристик полевого транзистора.
Оборудование:
транзистор КП303Г
прибор комбированный цифровой Щ 4300
блоки питания БСП-Б
амперметр АВО-5М1.
муфельная печь
соединительные провода.
Таблица.1. Некоторые табличные данные для полевого транзистора КП 303Г.
Ток стока при Ucи=10В, Uзи=0В
3 ― 12 мА
Напряжение отсечки при Ucи=10В, I=10мкА
8 В
Крутизна характеристики при Ucи=10В, Uзи=0В, f=50÷1500Гц
3 ― 7 мА/В
Ток затвора при Ucи=10В, Uзи=0В
не более 0,1 мА
Коэффициент шума при Ucи=10В, Uзи=0В, f=108 Гц
не более 4 дБ
ЭДС при Ucи=10В, Uзи=0В, f=103Гц
не более 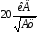
Входная ёмкость
не более 6 Пф
Проходящая ёмкость
не более 2 Пф
Нестабильность крутизны
не более 40%
Среднеквадратичный заряд при Ucи=10В, Uзи=0В, С=10 Пф
не более 0,6·107
Таблица 2. Стоко-затворные характеристики полевого транзистора КП303Г при t=20єС.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,00
1,50
Ток стока IС, мА,
при
напряжении затвор – исток
UСИ, В
5
10
12
5,50
5,70
5,85
4,61
4,81
4,95
4,00
4,07
4,16
3,50
3,90
3,95
2,70
2,75
2,90
1,15
1,18
1,21
0,02
0,07
0,09
Таблица 3. Стоко-затворные характеристики полевого транзистора КП303Г при t=25С.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,00
1,50
Ток стока IС, мА,
при
напряжении
затвор – исток
UСИ, В.
5
10
12
5,30
545
5,50
4,55
4,70
4,75
3,60
3,85
3,90
3,55
3,70
3,80
2,50
2,15
2,25
1,10
1,19
1,23
0,01
0,06
0,04
Таблица 4. Стоко-затворные характеристики полевого транзистора КП303Г при t=27С.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,00
1,50
Ток стока IС, мА,
при
напряжении
затвор – исток
UСИ, В.
5
10
12
5,10
5,50
5,56
4,50
4,70
4,85
3,85
3,90
4,00
3,70
3,60
3,30
2,30
1,50
2,50
1,09
1,20
1,26
0,01
0,05
0,08
Таблица 5. Стоко-затворные характеристики полевого транзистора КП303Гпри t=33єС.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,20
1,75
Ток стока IС, мА, при напряжении затвор – исток UСИ, В.
5
10
12
4,80
5,00
5,25
4,00
4,15
4,30
3,20
3,45
3,70
3,00
3,15
3,50
2,30
2,50
2,60
0,57
1,15
1,40
0,02
0,08
0,18
Таблица 6. Стоко-затворные характеристики полевого транзистора КП303Г при t=40єС.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,00
1,50
Ток стока IС, мА,
при
напряжении
затвор – исток
UСИ, В.
5
10
12
4,15
4,60
4,71
3,70
3,90
4,25
2,90
3,15
3,30
2,50
2,30
2,25
1,85
1,90
2,30
1,10
1,35
1,55
0,10
0,15
0,25
Таблица 7.Стоко-затворные характеристики полевого транзистора КП303Г при t=59єС.
Напряжение затвор-исток UЗИ, В.
0
0,20
0,40
0,60
0,80
1,00
1,50
Ток стока IС, мА,
при
напряжении
затвор – исток
UСИ, В.
5
10
12
4,00
4,25
4,45
3,15
4,00
4,30
2,75
3,00
3,15
2,10
2,50
2,80
1,90
2,15
2,40
0,80
1,00
1,25
00,05
0,15
0,35
Рисунок 54. График зависимости тока стока IC от напряжения затвор-исток UЗИ при постоянном напряжении сток -исток UСИ=5В.
Рисунок 55. График зависимости тока стока IC от напряжения затвор-исток UЗИ при постоянном напряжении сток -исток UСИ=10В.
Рисунок 56. График зависимости тока стока IC от напряжения затвор-исток UЗИ при постоянном напряжении сток -исток UСИ=12В.
Усилительные свойства прибора рассчитаем по формуле (63)
1.при t=20єС а) при UСИ=5В.

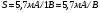
εS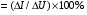 , εS=
, εS=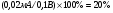
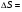 (εS
(εS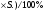 ,
,
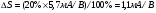
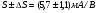
б) при UСИ=10В.
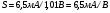
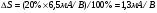
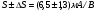
в) при UСИ=12В.
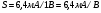
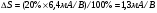
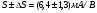
2. при t=59єС.
а) при UСИ=5В.
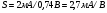
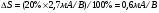
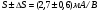
б) при UСИ=10В.
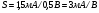
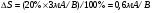
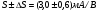
в) при UСИ=12В
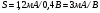
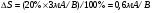
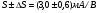
3. при t=40єС.
а) при UСИ=5В.
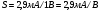
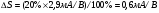
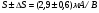
б) при UСИ=10В
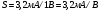
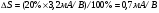
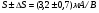
в) при UСИ=12В.
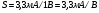
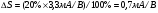
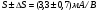
4. при t=33єС.
а) при UСИ=5В.
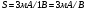
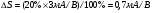
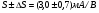
б) при UСИ=10В
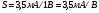
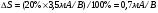
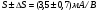
в) при UСИ=12В.
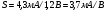
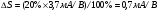
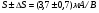
5. при t=27єС.
а) при UСИ=5В.
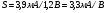
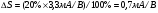
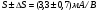
б) при UСИ=10В.
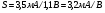
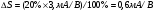
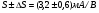
в) при UСИ=12В.
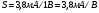
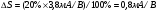
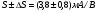
6.при t=25єС.
а) при UСИ=5В.
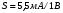
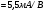
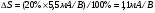
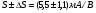
б) при UСИ=10В.
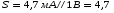
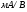
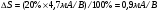
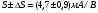
в) при UСИ=12В.
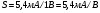
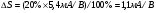
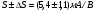
Таблица 8.Усилительные свойства транзистора КП303Г.
№,t,С.
Напряжение затвор-исток UЗИ, В
S,мА/В.
S±∆S, мА/В.
1.При t=20ºС
5
5,7
5,6±1,1
10
6,5
6,5±1,3
12
6,4
6,4±1,3
2.При t=65ºС.
5
2,8
2,8±0,6
10
3,0
3,0±0,6
12
2,7
2,7±0,5
3.
t=41ºС.
5
2,9
2,9±0,6
10
3,2
3,2±0,6
12
3,3
3,3±0,7
4.
t=35ºС
5
3,0
3,0±0,7
10
3,5
3,5±0,7
12
3,7
3,7±0,7
5.
t=27ºС
5
3,3
3,3±0,7
10
3,2
3,2±0,6
12
3,8
3,8±0,8
6.
t=22ºС
5
5,5
5,5±1,1
10
4,7
4,7±0,9
12
5,4
5,4±1,1
Вывод: Были определены усилительные свойства транзистора КП303Г (таблица 7). Усилительные свойства транзистора КП303Г при t=20єС следующие:
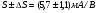 , при εS=20% при UСИ=5В.
, при εS=20% при UСИ=5В.
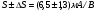 , при εS=20% при UСИ=10В.
, при εS=20% при UСИ=10В.
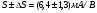 , при εS=20% при UСИ=12В.
, при εS=20% при UСИ=12В.
Полученные значения крутизны соответствуют теоретически ожидаемому.По теории при напряжении на сток-истоке равном 10В и частоте 50-1500Гц s=3-7мA\В.
Была изучена температурная зависимость полевого транзистора КП303г.Мною было замечено изменение статических характеристик передачи: с увеличением температуры наблюдается уменьшение тока стока и увеличение порогового напряжения UЗИПОР и уменьшение усилительных свойств прибора. Эти изменения вызваны в основном двумя физическими процессами:
1) С увеличением температуры в рабочем диапазоне температур уменьшается подвижность носителей заряда, что приводит к уменьшению тока стока;
2) Происходит перераспределение носителей по энергиям и смещение уровня Ферми к середине запрещенной зоны.
Всвязи с таким смещением уровня Ферми инверсионный слой образуется у поверхности полупроводника при меньших напряженностях электрического поля.
6.2 Статические характеристики полевого транзистора КП303Г и его температурная зависимость
Активная выходная проводимость g22И определяется наклоном стоковой характеристики в области насыщения (рис.52 б). Этот параметр находят построением треугольника АВС, по которому определяют приращения тока ΔIС и напряжения ΔUСИ. Тогда активная выходная проводимость
g22И = ΔIС/ ΔUСИ при UЗИ = const. (64)
Таблица 9. Стоковые характеристики полевого транзистора КП303Г при t=20єC.
Напряжение сток-исток UСИ, В
1
4
7
8
9
10
Ток стока IС, мА, при напряжении затвор-исток
UЗИ, В.
0
0,3
0,6
0,9
1,2
1,5
1,8
2,65
2,25
1,70
1,22
0,65
0,23
0,05
5,02
4,00
2,75
1,80
0,98
0,38
0,03
5,60
4,30
3,01
2,08
1,11
0,55
0,06
5,61
4,30
3,00
2,08
1,15
0,58
0,06
5,64
4,32
3,20
2,15
1,30
0,60
0,08
5,65
4,30
3,15
2,20
1,30
0,55
0,10
Рисунок 57. График зависимости тока стока IС от напряжения сток-истокUСИ при постоянном напряжении затвор-исток UЗИ при t=20єC.
Таблица 10. Стоковые характеристики полевого транзистора КП303Г при t=25єС.
Напряжение сток-исток UСИ, В
1
4
7
8
9
10
Ток стока IС, мА, при напряжении затвор-исток
UЗИ, В.
0
0,3
0,6
0,9
1,2
1,5
1,8
2,64
2,10
1,60
1,10
0,55
0,20
0,05
4,37
3,65
2,55
1,75
0,97
0,40
0,05
4,78
4,20
3,00
2,00
1,13
0,42
0,06
5,10
4,22
3,02
2,00
1,15
0,42
0,06
5,10
4,23
3,05
2,01
1,15
0,43
0,05
5,10
4,224
3,04
2,05
1,14
0,42
0,05
Рисунок 58. График зависимости тока стока IС от напряжения сток-истокUСИ при постоянном напряжении затвор-исток UЗИ при t=65єC.
Таблица 11. Стоковые характеристики полевого транзистора КП303Г при t=33є С.
Напряжение сток-исток UСИ, В
1
4
7
8
9
10
Ток стока IС, мА, при
напряжении затвор-исток UЗИ, В.
0
0,3
0,6
0,9
1,2
1,5
1,8
3,20
2,40
2,30
1,20
0,85
0,15
0,05
4,80
3,55
2,75
1,60
1,15
0,25
0,10
4,87
3,75
2,85
1,90
1,17
0,45
0,15
4,90
3,90
2,95
1,90
1,20
0,52
0,20
4,91
3,90
2,96
1,91
1,21
0,53
0,22
4,91
3,90
2,95
1,90
1,20
0,52
0,21
Рисунок 59. График зависимости тока стока IС от напряжения сток-истокUСИ при постоянном напряжении затвор-исток UЗИ при t=41єC.
Таблица 12. Стоковые характеристики полевого транзистора КП303Г при t=40С.
Напряжение сток-исток UСИ, В
1
4
7
8
9
10
Ток стока IС, мА, при напряжении затвор-исток UЗИ, В
0
0,3
0,6
0,9
1,2
1,5
1,8
3,70
2,10
1,17
1,20
0,85
0,35
0,07
4,50
3,65
2,65
1,55
1,05
0,45
0,10
4,55
3,85
2,70
1,73
1,15
0,47
0,15
4,54
3,84
2,70
1,75
1,14
0,52
0,14
4,60
3,86
2,71
1,76
1,13
0,49
0,14
4,60
3,86
2,71
1,77
1,15
0,49
0,14
Рисунок 60. График зависимости тока стока IС от напряжения сток-истокUСИ при постоянном напряжении затвор-исток UЗИ при t=35єC.
Таблица 12. Стоковые характеристики полевого транзистора КП303Г при t=59С.
Напряжение сток-исток UСИ, В
1
4
7
8
9
10
Ток стока IС, мА, при напряжении затвор-исток UЗИ, В.
0
0,3
0,6
0,9
1,2
1,5
1,8
3,47
3,00
2,75
1,94
0,90
0,20
0,05
3,57
3,10
2,80
2,00
1,05
0,30
0,05
4,27
3,87
3,45
2,69
1,45
0,50
0,07
4,54
4,00
3,52
2,70
1,50
0,54
0,10
4,53
4,01
3,53
2,72
1,51
0,53
0,10
4,55
4,00
3,55
2,75
1,50
0,55
0,09
Рисунок 61. График зависимости тока стока IС от напряжения сток-истокUСИ при постоянном напряжении затвор-исток UЗИ при t=27єC.
Для расчета активной выходной проводимости полевого транзистора КП303Г воспользуемся формулой (64)
εg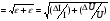
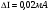
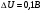
εg=20%
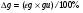
1.
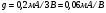

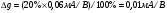

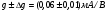
2. 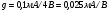
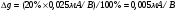
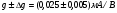
3. 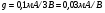
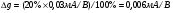
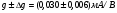
4. 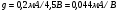
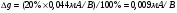
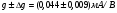
5 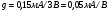
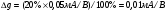
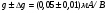
6. 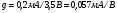
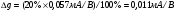
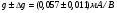
Таблица 13 Активная выходная проводимость транзистора КП303Г.
№ ; t,С
Активная выходная проводимость g, мА/В.
g±∆g, мА/В.
1, при t=20є С.
0,060
0,06±0,01
2, при t=59є С.
0,025
0,025±0,005
3, при t=40є С.
0,030
0,030±0,006
4, при t=33є С.
0,044
0,044±0,009
5, при t=27є С.
0,050
0,05±0,01
6, при t=25є С.
0,057
0,057±0,011
Вывод
В ходе эксперимента по полученнчм данным была найдена активная выходная проводимость g при различных температурах. Она была определенна по наклону стоковой характеристики в области насыщения. Активная выходная проводимость полевого транзистора КП303Г при температуре t=20єС имеет следующее значение:
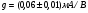 , при εg=20%.
, при εg=20%.
Теоретически ожидаемое значение проводимости составляет g теор= 0,07 мА/В.Полученные данные согласуются с теоретически ожидаемыми.
В ходе изучения зависимости стоковых характеристик от температуры было выяснено:с увеличением температуры наблюдалось изменение тока стока ― ток стока уменьшается с увеличением температуры.
Литература
Автоматизация и проектирование матричных КМОП БИС. М.: Радио и связь,1991.-256с.
Андреев В.А. Мощный полевой транзистор./Что нового в науке и технике,2005.-34-37стр
Ансельм А.И. Введение в теорию полупроводников. М.: Советское радио,1978.-354с.
Быков Р.Е. и др. Телевидение- Москва: Высшая школа,1990.-167с.
Викулин И.М. Стафеев В.И. Физика полупроводниковых приборов. - М.: Радио и связь,1990.-264с.
Воробьев Ю.В. и др. Методы исследования полупроводников – Киев: Высшая школа,1988.-230с.
Гергель В.А. Зеленый А.П. Особенности перезарядки поверхностных состояний в МДП-структурах./Микроэлектроника,1998.-93-94стр.
Ефимов И. Е. и др. Микроэлектроника: проектирование, виды микросхем, функциональная микроэлектроника. М.: Высшая школа,1987.- 416с.
Жеребцов И.П. Основы Электроники. – Л.:Эноргоатомиздат,1990.- 352с.
Зи С. Физика полупроводниковых приборов: в 2-х книгах М.:Мир,1984.-456с.
Игнатов А.Н. Полевые транзисторы и их применение. - М.: Радио и связь,1984.-217с.
Кобболд Р. Теория и применение полевых транзисторов.-Л.:Энергия,1975.-304с.
Майоров С.А. Полевые транзисторы, технологии и их применение. - М.: Советское радио,1971.-230с.
Митрофанов О.В. и др. Микроэлектроника. – М.: Высшая школа,1987.-212с
Неизвестный С.И. И Никулин О.Ю. Приборы с зарядовой связью. Устройство и основные принципы действия./Электротехника,2005.- 14-20стр.
Неизвестный С.И. И Никулин О.Ю.Важные свойства, основные характеристики ПЗС и телесистема на их основе ./Электротехника,2005.- 14-20стр.
Носов Ю.Р. и др. Полупроводниковые приборы с зарядовой связью. – М.: Советское радио,1976.-144с.
Пасынков В.В. и др. Полупроводниковые приборы.- М.: Высшая школа, 1987.-479с.
Пикуса Г.Е. Физика поверхности полупроводников. – М.: Издательство иностранной литературы,1959.-432с.
Приборы с зарядовой связью.(Сборник статей)-М.:Знание,1983.-63с.
Рембеза С.И. Методы исследования основных параметров полупроводников.- Воронеж: Издательство Воронежского университета,1989.-221с.
Ричман П. Физические основы полевых транзисторов с изолированным затвором.- М.: Советское радио, 1971.-142с.
Севин Л.И. Полевые транзисторы. М.: Советское радио,1968.-184с.
Столярский Э. Измерение параметров транзисторов. М.: Советское радио,1989.-234с.
Сыноров В.Ф. Чистов Ю.С. Физика МДП-структур. В.: Издательство воронежского университета,1989.-223с.
Физическая энциклопедия 4т.Гл. редактор Прохоров А.М. М.: Большая российская энциклопедия,1994.-704с.
Шалимова К.В. Физика полупроводников. – М.:Энергия,1971.- 312с.
Эндерлайн Р. Микроэлектроника для всех. Введение в мир интегральных микросхем: основы функционирования, технология изготовления и применения. М.: Мир, 1989.-192с.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ