Процесс создания линии электропередач этапы факторы и результат

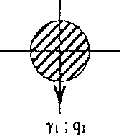
 Содержание
Содержание
Процесс создания линии электропередач: этапы, факторы и результат
Совершенно гибкая нить та, которая сопротивляется только растяжению. У идеальной гибкой нити жесткость на кручение, изгиб, сдвиг и сжатие равны нулю. Это означает, что гибкая нить может воспринимать усилия только на растяжение, при этом растягивающие усилия направлены по касательной к продольной оси нити.
На практике очень много систем, которые рассматриваются как гибкие нити. Это: воздушные линии электропередач, провода электрифицированных железных дорог, цепи висячих мостов, канатные дороги и т.д.
Рассчитать воздушную линию электропередачи, это значит обеспечить условие прочности провода <= [], т.е. действующие значения напряжения, возникающие в проводе под действием внешних нагрузок, не должны превышать допускаемых значений. Основными внешними факторами, изменяющими напряжения в проводе, являются: температура внешней среды и действующая на провод нагрузка. Эти параметры и вызывают различную по величине деформацию провода. Деформация и напряжение взаимосвязаны и вызываются они действием внешних сил. Изменение условий эксплуатации - это изменение внешних сил, а, следовательно, изменение деформаций и напряжений.
Наша задача: знать, как определить внешние силы и внутренние факторы - напряжение, деформацию, а также как будут изменяться эти параметры при изменении условий эксплуатации.
Для этого мы рассмотрим различные стороны этой задачи:
статическую, которая позволит определить ряд силовых параметров и форму кривой провисания нити под действием внешних нагрузок;
геометрическую, дающую возможность выяснить вопросы деформации от воздействия различных нагрузок;
физическую, - определить деформацию от температурных воздействий, а также связать во едино оба вида деформаций и получить уравнение совместной деформации.
Решить вопросы о действующем значении напряжения и связанной с ним стрелы провисания, а также установить связь этих параметров при изменении условий эксплуатации поможет уравнение состояния нити (провода).
Рассмотрим эти вопросы подробней.
В качестве гибкой нити будем рассматривать провода воздушной линии. При этом могут быть использованы однопроволочные и многопроволочные провода, скрученные из алюминиевых и стальных проволок для придания механической прочности в сочетании с высокой электропроводностью. Число проводов в фазе может быть: n = 1; n = 2; n = 3; n = 4.
n = 1
n = 2
n = 3
n = 4
Исходные данные:
Передаваемое напряжение U (кВ): 220;
Характеристика местности: населенная;
Используемый провод: АСО-700;
Температура установки провода (монтажа): t0уст = +150С;
Разноуровневая подвеска с перепадом высот "h", м: 0;
Температура гололедообразования: t0гол = - 7,50C;
Скоростной напор Q, кг/м2: 27;
Максимальная температура: t0max = +400C;
Минимальная температура: t0min = - 350C;
Расстояние между опорами, l, м: 200;
Толщина стенки льда, "с", м: 22;
1. По справочной литературе находим необходимые данные для расчетов:
а) номинальное сечение: 700 мм2;
б) число и диаметр проволок в проводе:
544,10 мм (алюминий)
192,5 мм (сталь);
в) сечение:
Fa=712 мм2
Fс=93,3 мм2
Сечение провода в целом: F=Fa+Fc=805.3 мм2;
г) расчетный диаметр провода: d=37.1 мм;
д) расчетный вес провода: G0=2.756 кг/м;
е) отношение сечений: Fa/Fc=7,67;
ж) приведенный модуль упругости: Епр=7880 кг/мм2;
з) коэффициент температурного линейного расширения провода: =19,7810-6 1/град;
2. Так как местность населенная и напряжение 220 кВ, то расстояние между землей и нижней частью провода составляет: h=8 м;
3. Вид сечения фазы:
4. Значение скорости ветра определяется через скоростной напор:
Vmax=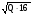 =20.785 м/с.
=20.785 м/с.
5. Предел прочности: nч=27 кг/мм2;
[] I=10.00 кг/мм2;
[] II=11.35 кг/мм2;
[] III=6.75 кг/мм2;
Выделим режимы эксплуатации:
I - Минимальная температура: tmin=-35 0C;
IIа - Максимальная нагрузка; режим наибольшего скоростного напора: Vmax=20.785 м/с; t=-5 0C, гололед отсутствует;
IIб - Режим наибольшего гололеда: V=Vmax0.5=10.3925 м/с;
III - Режим среднегодовых температур, гололед и ветер отсутствуют; tср=-50C;
IV - Режим максимальных температур: tmax=+40 0C;
Внешние нагрузки на провод
Провода воздушных линий испытывают действие механических нагрузок, направленных по вертикали (вес провода и гололед) и по горизонтали (давление ветра), в результате чего в металле проводов возникают напряжения растяжения. На величину последних влияет также и температура окружающего воздуха, что заставляет учитывать ее в расчетах.
На практике считают, что все нагрузки в пролете между двумя опорами распределены равномерно по длине проводов и являются статическими, а отдельных порывов ветра, создающих динамический характер нагрузки, не учитывают, хотя они и возможны.
В расчет механической прочности проводов вводят понятие удельных нагрузок. Это интенсивность погонной нагрузки “q", отнесенная к площади поперечного сечения провода (нити), т.е. это нагрузка, действующая на 1 м провода и приходящаяся на 1 мм2 площади поперечного сечения.
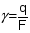
где: q - погонная нагрузка на участке нити (провода) длиной 1 м; н/м; н/мм; кг/мм;
F - теоретическая площадь поперечного сечения провода, мм2.
Если провод рассматривается как многопроволочный, т.е. состоящий из алюминия Fa и стали Fc, то:
F = Fa + Fc
Определим удельные нагрузки на провода.
Нагрузка от собственного веса
1 ; q1
Удельная нагрузка провода от веса провода 1:
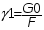 [кг/м*мм2] или
[кг/м*мм2] или 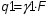
где: G0 - вес одного метра провода, кг;
F - расчетное действительное сечение всего провода, мм2;
q1 - вес единицы длины провода.
Производим расчет:
Площадь провода в фазе: Fфазы=Fn=805.33=2415.9 мм2;
Диаметр фазы: dфазы= dn =37.13=111.3 мм;
Вес провода фазы G=G0n=2.7563=8.268 кг/м;
Удельная нагрузка от собственного веса:
1 ; q1
Нагрузка от гололеда
c
c
d
2
Считается, что все виды обледенения провода представляют собой цилиндрическую форму. Лед с объёмным весом q0 = 0.910-3 кг/см3. Стенка льда равномерная, толщиной “c”.
2
1
3
Удельная нагрузка от веса льда 2 определяется:
2 = G / F или q2 = 2 Fл
(G = q, если рассматривается вес единицы длины),
где: G - вес пустотелого цилиндра гололеда, кг;
F - поперечное сечение ледяного покрытия, мм2.
Объем гололеда на проводе длиной 1 м:
V = (103/4) [ (d+2c) - d2] = c (d+c) 103, [мм3]
Вес гололеда на проводе:
G = Vq0 = c (d+c) q0 = 0.00283c (d+c), [кг]
отсюда:
2 = G / F = 0.00283 [c (d+c) /F], [кг/ммм2]
2=Gвес льда/F=0,00283 [с (с+d) /F] =
=0.00283 [22 (22+37.1) /805.3] =4.5710-3 кг/ (ммм2)
Нагрузка от веса провода и гололеда
Эти нагрузки действуют в одной вертикальной плоскости и поэтому складываются арифметически:
3 = 1+2 [кг/ммм2]
3=1+2=810-3 кг/ (ммм2)
Нагрузка от давления ветра
Давление ветра, направленного горизонтально под углом 90 к поверхности провода, определяется по формуле:
P = CxQS [кг]
где: Q = U2/16 - скоростной напор ветра, кг/м2;
U - скорость ветра, м/с;
- коэффициент, учитывающий неравномерность скорости ветра по длине пролета, зависящий от скорости ветра или скоростного напора Q;
Cx - аэродинамический коэффициент: при d 20 мм Cx = 1.1
d 20 мм Cx = 1.2, а также для всех проводов, покрытых гололедом;
S - площадь диаметрального сечения провода, м2.
Давление ветра на 1 м длины провода диаметром d (мм) можно подсчитать по формуле:
P = CxQ (d/103) [кг/м]
а удельную нагрузку от ветра на провод, свободный от гололеда, - по формуле:
4 = (CxQd) / (103F) [кг/ммм2]
При наличии гололеда, поверхность провода, на которую давит ветер, увеличивается. Удельная нагрузка при этом будет:
5 = (CxQ (d+2c)) / (103F) [кг/ммм2]
5
c
c
d
Q
Удельная нагрузка от давления ветра на провод без гололеда, (согласно таблице 1 текста), т.к. Q=27, то =1; Сx=1.1
4=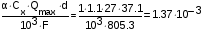 кг/ (ммм2)
кг/ (ммм2)
Удельная нагрузка от давления ветра на провод покрытый льдом:
Q=0.25Qmax=6.75 кг/м2, принимаем Q=14кг/м2, тогда =1, c=22 мм
5=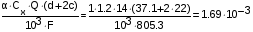 кг/ (ммм2)
кг/ (ммм2)
Суммарные нагрузки
6
1
4
7
2
5
1
3
Для нахождения результирующих нагрузок на провод, вытекающих из условий эксплуатации, надо найти геометрическую сумму действующих на него вертикальных и горизонтальных нагрузок.
Так, суммарная удельная нагрузка на провод от его собственного веса и давления ветра на провод равна:
6=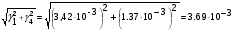 кг/ (ммм2)
кг/ (ммм2)
Суммарная удельная нагрузка на провод от веса провода, веса гололеда и давления ветра составляет:
7=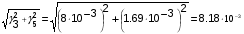 кг/ (ммм2)
кг/ (ммм2)
Согласно расчетам, режим IIб является самым опасным:
7=8.1810-3 кг/ (ммм2).
Понятие о критическом пролете
Рассчитывая провод на прочность, важно установить, при каком из перечисленных режимов напряжения в проводе достигнут допускаемых значений. Этот режим называется исходным.
Для нахождения исходного режима необходимо определить критические пролеты.
Сравнивая два режима, под критическим пролетом будем понимать такой пролет Lкр, при котором напряженное состояние провода в обоих режимах будет равноопасным, т.е. напряжения в проводе будут равны допускаемым для каждого из сравниваемых режимов.
Исходный режим определяется при сравнении величин заданного пролета L с величиной Lкр.
Определим исходный режим, при котором напряжение в проводе максимально допустимое. Для этого надо найти три значения Lкр:
Сравним два режима I и II:
Режим I
tmin=-35
1=3,4210-3
I= [] I
Lкр2-?
Режим II
tгол=-7.5
max=7=8,1810-3
II= [] II
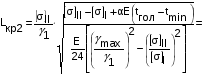
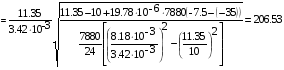 м
м
Сравним другие режимы:
Сравним режимы I и III:
Режим I
tmin=-35
1=3,4210-3
I= [] I
Lкр1-?
Режим III
tср=-5
1=3,4210-3
III= [] III
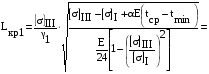
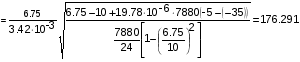 м
м
Сравним режимы III и II
Режим III
tср=-5
1=3,4210-3
III= [] III
Lкр3-?
Режим II
tгол=-7.5
max=7=8,1810-3
II= [] II
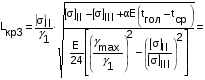
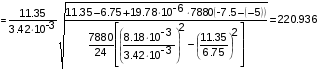 м
м
Мы получили неравенство: Lкр3> L1> Lкр1. Самым опасным режимом будет режим среднегодовых температур (Режим III).
Подвеска провода
Подвеска провода осуществляется в безветренные дни, когда нет гололеда, но при любой температуре. При этом нагрузкой на провод есть собственный вес.
200
0
L
В таких условиях, выполняя работы по подвеске провода, необходимо обеспечить такой подвес провода fподв, а, следовательно и такое напряжение подв, чтобы в самых наихудших условиях эксплуатации воздушной линии выполнялось условие прочности провода, т.е.: подв [].
Определяем стрелу провеса для исходного режима:
L=L1cos=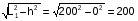
cos=L/L1=200/200=1
Определяем стрелу провеса для исходного режима (III):
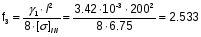 м
м
Пользуясь уравнением состояния нити, определим значения напряжений для других условий эксплуатации.
Определим напряжение в проводе при максимальной температуре:
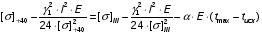
подставив значения, будем иметь:
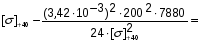
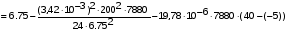
получим:

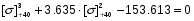
Примем: [] +40=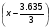 или [] +40=x-1.212
или [] +40=x-1.212
[] +403x3-3.635x2+4.404x-1.779
[] +402x2+2.423x+1.468
Подставляя в исходное уравнение, получим:
x3-3.635x2+4.404x-1,779+3,635x2-8.809x+5,337-153.613=0
получим:
x3-4.405x-150.055=0 x3-31,468x-2 75.028
p=1.468 q=75.028
p3=3.164 q2=5629.141
q2 > p3.
Получим случай №2: определяем угол из уравнения
ch=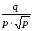 : ch = 42.178
: ch = 42.178
= 4.435, тогда x=+2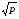 ch (/3) =2.423ch (4.435) =5.590
ch (/3) =2.423ch (4.435) =5.590
[] +40=4.378 кг/мм2
Определим провес:
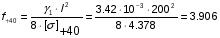 м
м
Определим напряжение в проводе при гололеде без ветра:
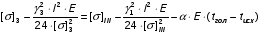
подставив значения, будем иметь:
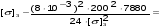
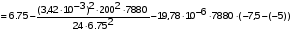
получим:
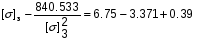
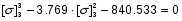
Примем: [] 3=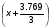 или [] 3=x+1.256
или [] 3=x+1.256
[] 33x3+3.769x2+4.735x+1.983
[] 32x2+2.513x+1.578
Подставляя в исходное уравнение, получим:
x3+3.769x2+4.735x+1,983-3,769x2-9.47x-5,949-840.533=0
получим:
x3-4.735x-844.499=0 x3-31,578x-2 422.249
p=1.578 q=422.249
p3=3.932 q2=178294.64
q2 > p3. Получим случай №2:
Определяем угол из уравнения
ch=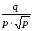 : ch = 213.042
: ch = 213.042
= 6.054, тогда x=+2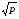 ch (/3) =2.512ch (2.018) =9.619
ch (/3) =2.512ch (2.018) =9.619
[] 3=10.875 кг/мм2
Определим провес:
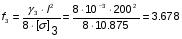 м
м
Определим напряжение в проводе при максимальной нагрузке, т.е. обледенение с ветром:
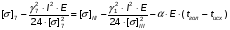
подставив значения, будем иметь:
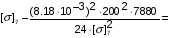
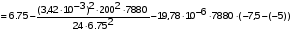
получим:
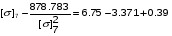
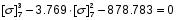
Примем: [] 7=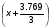 или [] 7=x+1.256
или [] 7=x+1.256
[] 73x3+3.769x2+4.735x+1.983
[] 72x2+2.513x+1.578
Подставляя в исходное уравнение, получим:
x3+3.769x2+4.735x+1,983-3,769x2-9.47x-5,949-878.783=0
получим:
x3-4.735x-882.749=0 x3-31.578x-2 441.374
p=1.578 q=441.374
p3=3.932 q2=194811.449
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=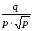 : ch = 222.578
: ch = 222.578
= 6.098, тогда x=+2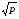 ch (/3) =2.512ch (2.033) =9.757
ch (/3) =2.512ch (2.033) =9.757
[] 7=11.014 кг/мм2
Определим провес:
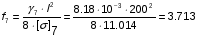 м
м
Определим напряжение в проводе при минимальной температуре:
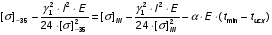
подставив значения, будем иметь:
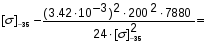
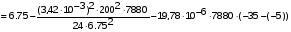
получим:
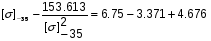
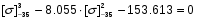
Примем: [] -35=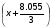 или [] -35=x+2.685
или [] -35=x+2.685
[] -353x3+8.055x2+21.628x+19.357
[] -352x2+5.370x+7.209
Подставляя в исходное уравнение, получим:
x3+8.055x2+21.628x+19,357-8,055x2-43.255x-58,07-153.613=0
получим:
x3-21.627x-192.326=0 x3-37.209x-2 96.163
p=7.209 q=96.163
p3=374.681 q2=9247.380
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=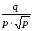 : ch = 4.968
: ch = 4.968
= 2.286, тогда x=+2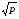 ch (/3) =5.37ch (0.762) =7.006
ch (/3) =5.37ch (0.762) =7.006
[] -35=9.691 кг/мм2
Определим провес:
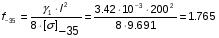 м
м
Со всех вышеуказанных расчетов можно сделать следующий важный вывод - рассчитанные механические напряжения в проводе при гололеде без ветра, при гололеде с ветром и при режиме минимальных температур оказываются большими от допустимого механического напряжения в проводе для нашего исходного режима (Режим III [] III = 6.75). На основе этих данных делаем вывод о том, что провод марки АСО-700 не выдержит механических усилий при указанных режимах своей работы и разрушится. Следовательно, для проведения следующих расчетов мы должны взять для рассмотрения провод другой марки. Например, возьмем в качестве исходного провода для ЛЭП провод марки АСУ-400 и повторим все вышеуказанные расчеты. После этих расчетов сделаем соответствующие выводы о целесообразности проведения конечных расчетов.
Исходные данные:
1. Передаваемое напряжение U (кВ): 220;
2. Характеристика местности: населенная;
3. Используемый провод: АСУ-400;
4. Температура установки провода (монтажа): t0уст = +150С;
5. Разноуровневая подвеска с перепадом высот "h", м: 0;
6. Температура гололедообразования: t0гол = - 7,50C;
7. Скоростной напор Q, кг/м2: 27;
8. Максимальная температура: t0max = +400C;
9. Минимальная температура: t0min = - 350C;
10. Расстояние между опорами, l, м: 200;
11. Толщина стенки льда, "с", м: 22;
1. По справочной литературе находим необходимые данные для расчетов:
а) номинальное сечение: 400 мм2;
б) число и диаметр проволок в проводе:
304,12 мм (алюминий)
192,5 мм (сталь);
в) сечение:
Fa=400 мм2
Fс=93,3 мм2
Сечение провода в целом: F=Fa+Fc=493.3 мм2;
г) расчетный диаметр провода: d=29.0 мм;
д) расчетный вес провода: G0=1.840 кг/м;
е) отношение сечений: Fa/Fc=4,28;
ж) приведенный модуль упругости: Епр=8900 кг/мм2;
з) коэффициент температурного линейного расширения провода: =18,2610-6 1/град;
2. Так как местность населенная и напряжение 220 кВ, то расстояние между землей и нижней частью провода составляет: h=8 м;
3. Вид сечения фазы:
4. Значение скорости ветра определяется через скоростной напор:
Vmax=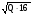 =20.785 м/с.
=20.785 м/с.
5. Предел прочности: nч=31 кг/мм2;
[] I=11.47 кг/мм2;
[] II=13.00 кг/мм2;
[] III=7.75 кг/мм2;
Выделим режимы эксплуатации:
I - Минимальная температура: tmin=-35 0C;
IIа - Максимальная нагрузка; режим наибольшего скоростного напора: Vmax=20.785 м/с; t=-5 0C, гололед отсутствует;
IIб - Режим наибольшего гололеда: V=Vmax0.5=10.3925 м/с;
III - Режим среднегодовых температур, гололед и ветер отсутствуют; tср=-50C;
IV - Режим максимальных температур: tmax=+40 0C;
Производим расчет:
1. Площадь провода в фазе: Fфазы=Fn=493.33=1479.9 мм2;
Диаметр фазы: dфазы= dn =293=87 мм;
Вес провода фазы G=G0n=1.843=5.52 кг/м;
2. Удельная нагрузка от собственного веса:
1=G0/F=1.84/493.3=3.7299810-3 кг/ (ммм2)
3. Удельная нагрузка от гололеда:
2=Gвес льда/F=0,00283 [с (с+d) /F] =
=0.00283 [22 (22+29) /493.3] =6.4367710-3 кг/ (ммм2)
4. Удельная нагрузка от собственного веса провода и гололеда:
3=1+2=0.01017 кг/ (ммм2)
5. Удельная нагрузка от давления ветра на провод без гололеда, (согласно таблице 1 текста), т.к Q=27, то =1; Сx=1.1
4=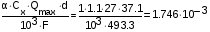 кг/ (ммм2)
кг/ (ммм2)
6. Удельная нагрузка от давления ветра на провод, покрытый льдом:
Q=0.25Qmax=6.75 кг/м2, принимаем Q=14кг/м2, тогда =1, c=30 мм
5=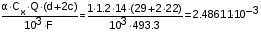 кг/ (ммм2)
кг/ (ммм2)
7. Суммарная удельная нагрузка на провод от его собственного веса и давления ветра на провод равна:
6=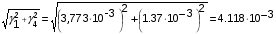 кг/ (ммм2)
кг/ (ммм2)
8. Суммарная удельная нагрузка на провод от веса провода, веса гололеда и давления ветра составляет:
7=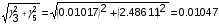 кг/ (ммм2)
кг/ (ммм2)
Согласно расчетам, режим IIб является самым опасным:
7=0.01047 кг/ (ммм2).
Определяем исходный режим:
Сравним два режима I и II:
Режим I
tmin=-35
1=3,7299810-3
I= [] I
Lкр2-?
Режим II
tгол=-7.5
max=7=0.01047
II= [] II
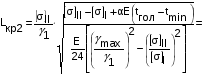
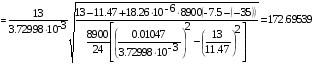 м
м
Сравним другие режимы:
Сравним режимы I и III:
Режим I
tmin=-35
1=3,7299810-3
I= [] I
Lкр1-?
Режим III
tср=-5
1=3,7299810-3
III= [] III
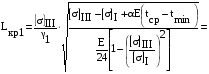
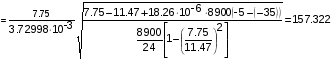 м
м
Сравним режимы III и II
Режим III
tср=-5
1=3,7299810-3
III= [] III
Lкр3-?
Режим II
tгол=-7.5
max=7=0.01047
II= [] II
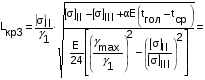
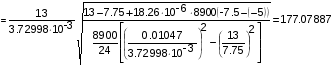 м
м
200
0
L
В этом случае физический смысл имеет Lкр2. Самым опасным режимом будет режим максимальных нагрузок (IIб), т.к L> Lкр2.
Подвеска провода
Определяем стрелу провеса для исходного режима:
L=L1cos=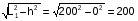
cos=L/L1=200/200=1
Определяем стрелу провеса для исходного режима (III):
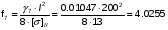 м
м
Пользуясь уравнением состояния нити, определим значения напряжений для других условий эксплуатации.
Определим напряжение в проводе при максимальной температуре:
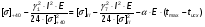
подставив значения, будем иметь:
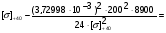
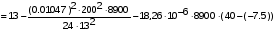
получим:
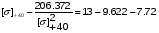
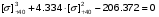
Примем: [] +40=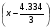 или [] +40=x-1.445
или [] +40=x-1.445
[] +403x3-4.334x2+6.261x-3.015
[] +402x2-2.889x+2.087
Подставляя в исходное уравнение, получим:
x3-4.334x2+6.261x-3,015+4,334x2-12.521x+9,045-206.372=0
получим:
x3-6.261x-200.342=0 x3-32,087x-2 100.171
p=2.087 q=100.171
p3=9.091 q2=10034.29
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=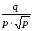 : ch = 33.222
: ch = 33.222
= 4.196, тогда x=+2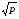 ch (/3) =2.889ch (1.399) =6.208
ch (/3) =2.889ch (1.399) =6.208
[] +40=4.76293 кг/мм2
Определим провес:
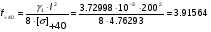 м
м
Определим напряжение в проводе при гололеде без ветра:
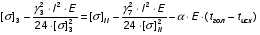
подставив значения, будем иметь:
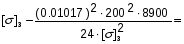
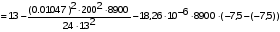
получим:
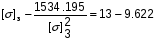
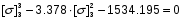
Примем: [] 3=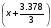 или [] 3=x+1.126
или [] 3=x+1.126
[] 33x3+3.378x2+3.804x+1.428
[] 32x2+2.252x+1.268
Подставляя в исходное уравнение, получим:
x3+3.378x2+3.804x+1,428-3,378x2-7.607x-4,283-1534.195=0
получим:
x3-3.803x-1537.05=0 x3-31,268x-2 768.525
p=1.268 q=768.525
p3=2.038 q2=590630.829
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=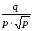 : ch = 538.308
: ch = 538.308
= 6.982, тогда x=+2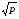 ch (/3) =2.252ch (2.327) =11.651
ch (/3) =2.252ch (2.327) =11.651
[] 3=12.77698 кг/мм2
Определим провес:
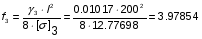 м
м
Определим напряжение в проводе при среднегодовой температуре:
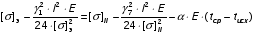
подставив значения, будем иметь:
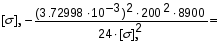
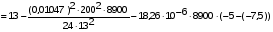
получим:
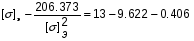
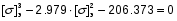
Примем: [] э=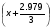 или [] э=x+0.993
или [] э=x+0.993
[] э3x3+2.979x2+2.958x+0.979
[] э2x2+1.986x+0.986
Подставляя в исходное уравнение, получим:
x3+2.979x2+2.958x+0,979-2,979x2-5.916x-2,937-206.373=0
получим:
x3-2.958x-208.331=0 x3-30.986x-2 104.166
p=0.986 q=104.166
p3=0.959 q2=10850.472
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=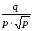 : ch = 106.392
: ch = 106.392
= 5.360, тогда x=+2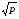 ch (/3) =1.986ch (1.787) =6.095
ch (/3) =1.986ch (1.787) =6.095
[] э=7.08739 кг/мм2
Определение провеса провода для этого режима не имеет практического смысла.
Определим напряжение в проводе при минимальной температуре:
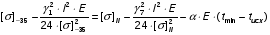
подставив значения, будем иметь:
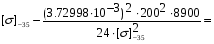
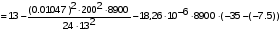
получим:
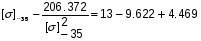
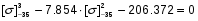
Примем: [] -35=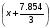 или [] -35=x+2.618
или [] -35=x+2.618
[] -353x3+7.854x2+20.562x+17.944, [] -352x2+5.236x+6.854
Подставляя в исходное уравнение, получим:
x3+7.854x2+20.562x+17,944-7,854x2-41.124x-53,831-206.372=0
получим:
x3-20.562x-242.259=0 x3-36.854x-2 121.13
p=6.854 q=121.13
p3=321.968 q2=14672.38
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=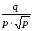 : ch = 6.751
: ch = 6.751
= 2.597, тогда x=+2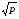 ch (/3) =5.236ch (0.866) =7.324
ch (/3) =5.236ch (0.866) =7.324
[] -35=9.94216 кг/мм2
Определим провес:
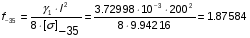 м
м
По вышеизложенным расчетам мы можем сделать соответствующий вывод о пригодности замененного провода марки АСУ-400 для указанных исходных условий эксплуатации данного провода. Теперь мы можем продолжать дальнейшие расчеты.
Выпишем и сравним все значения провесов, полученных для различных режимов эксплуатации:
а) Режим максимальных температур: f+40=3,91564 м
б) Режим гололеда без ветра: f3=3.97854 м
в) Режим минимальных температур: f-35=1.87584 м
г) Режим гололеда с ветром: f7=4,0255 м
Видим, что наибольший провес получается при режиме максимальных нагрузок - обледенение с ветром: f7=4,0255 м
Согласно этим данным по таблице 1, приложения 4, определяем высоту опоры: 8+4,0255=12,0255 12 м.
Расчет монтажного графика
Подвеска провода осуществляется в безветренные дни, когда нет гололеда, но при любой температуре. При этом нагрузкой на провод есть собственный вес, т.е.:
подв = п = 1, температура t = tподвески.
В таких условиях, выполняя работы по подвеске провода, необходимо обеспечить такой подвес провода fподв, а, следовательно и такое напряжение подв, чтобы в самых наихудших условиях эксплуатации воздушной линии выполнялось условие прочности провода, т.е.:
подв [].
Итак: наихудшими условиями эксплуатации являются условия при исходном режиме, поэтому, сравнивая через уравнения связи два состояния провода: исходного режима и режима подвески (монтажа), определим необходимое значение напряжения при подвеске.
Если принять:
Исходный режим
tисх
исх
исх = [] исх
Режим
tподвески
1 = п
подв =?
Уравнение связи при этом будет:
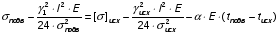
При этом поступают таким образом: задаются несколькими (4-5) значениями температуры подвеса (монтажа) провода в пределах от tmin до tmax, и решают вышеуказанное уравнение. Строят монтажные графики fподв = f (tподв), т.е. зависимость монтажного провеса провода от температуры или Нподв = f (tподв), или подв = f (tподв). Эти величины определяют по формулам:
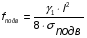
Hподв = подв F
Результаты заносят в соответствующую таблицу.
По результатам расчетов строят графики монтажа провода.
При выполнении монтажа провода для замера параметра fподв используют мерные рейки. и геодезические приборы.
Для достижения подв используют натяжные устройства через динамометр, определяют Нподв, соответствующую fподв, подв, для данной tподв.
Разобьем интервал температур от tmin до tmax на 6 равных отрезков:
tмонт1
tмонт2
tмонт3
tмонт4
tмонт5
tмонт6
-35C
-20C
-5C
+10C
+25C
+40C
1) Найдем напряжение в проводе при tмонт1 = - 35C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт1= - 35C
1=п=3.7299810-3
монт1 =?
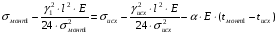
подставив значения, будем иметь:
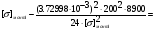
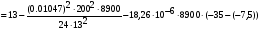
получим:
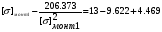
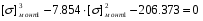
Примем: [] монт1=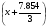 или [] монт1=x+2.618
или [] монт1=x+2.618
[] монт13x3+7.854x2+20.562x+17.944
[] монт12x2+5.236x+6.854
Подставляя в исходное уравнение, получим:
x3+7.854x2+20.562x+17,944-7,854x2-41.124x-53,831-206.373=0
получим:
x3-20.562x-242.26=0 x3-36,854x-2 121.13
p=6.854 q=121.13, p3=321.968 q2=14672.501
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=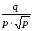 : ch = 6.751
: ch = 6.751
= 2.597, тогда x=+2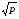 ch (/3) =5.236ch (0.866) =7.324
ch (/3) =5.236ch (0.866) =7.324
[] монт1=9.94216 кг/мм2
Определим провес провода:
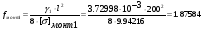 м
м
Определим натяжение провода:
Hмонт1 = монт1 F = 9.94216 493.3 = 4904.46753 кг.
2) Найдем напряжение в проводе при tмонт2 = - 20C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт2= - 20C
1=п=3.7299810-3
монт2 =?
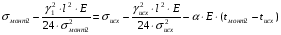
подставив значения, будем иметь:
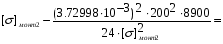
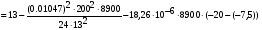
получим:
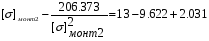
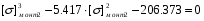
Примем: [] монт2=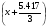 или [] монт2=x+1.806
или [] монт2=x+1.806
[] монт23x3+5.417x2+9.781x+5.887
[] монт22x2+3.611x+3.26
Подставляя в исходное уравнение, получим:
x3+5.417x2+9.781x+5,887-5,417x2-19.561x-17,659-206.373=0
получим:
x3-9.782x-218.148=0 x3-33,26x-2 109.074
p=3.26 q=109.074
p3=34.659 q2=11897.094
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=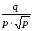 : ch = 18.527
: ch = 18.527
= 3.612, тогда x=+2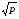 ch (/3) =3.611ch (1.204) =6.56
ch (/3) =3.611ch (1.204) =6.56
[] монт2=8.36556 кг/мм2
Определим провес провода:
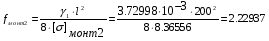 м
м
Определим натяжение провода:
Hмонт2 = монт2 F = 8.36556 493.3 = 4126.73075 кг.
3) Найдем напряжение в проводе при tмонт3 = - 5C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт3= - 5C
1=п=3.7299810-3
монт3 =?
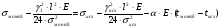
подставив значения, будем иметь:
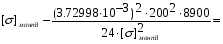
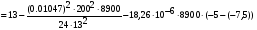
получим:
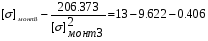
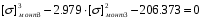
Примем: [] монт3=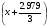 или [] монт3=x+0.993
или [] монт3=x+0.993
[] монт33x3+2.979x2+2.958x+0.979
[] монт32x2+1.986x+0.986
Подставляя в исходное уравнение, получим:
x3+2.979x2+2.958x+0,979-2,979x2-5.916x-2,937-206.373=0
получим:
x3-2.958x-208.331=0 x3-30,986x-2 104.166
p=3.26 q=109.074
p3=0.959 q2=10850.472
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=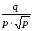 : ch = 106.392
: ch = 106.392
= 5.36, тогда x=+2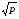 ch (/3) =3.611ch (1.787) =6.095
ch (/3) =3.611ch (1.787) =6.095
[] монт3=7.08739 кг/мм2
Определим провес провода:
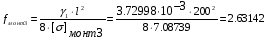 м
м
Определим натяжение провода:
Hмонт3 = монт3 F = 7.08739 493.3 = 3496.20949 кг.
4) Найдем напряжение в проводе при tмонт4 = +10C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт4= +10C
1=п=3.7299810-3
монт4 =?
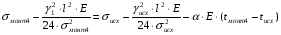
подставив значения, будем иметь:
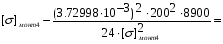
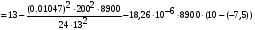
получим:
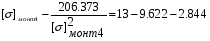
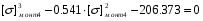
Примем: [] монт4=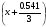 или [] монт4=x+0.18
или [] монт4=x+0.18
[] монт43x3+0.541x2+0.098x+0.006
[] монт42x2+0.361x+0.033
Подставляя в исходное уравнение, получим:
x3+0.541x2+0.098x+0,006-0,541x2-0.195x-0,018-206.373=0
получим:
x3-0.097x-206.385=0 x3-30,033x-2 103.192
p=0.033 q=103.192
p3=0.001 q2=10648.671
q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=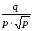 : ch = 17612.568
: ch = 17612.568
= 10.47, тогда x=+2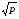 ch (/3) =0.363ch (3.49) =5.915
ch (/3) =0.363ch (3.49) =5.915
[] монт4=6.09553 кг/мм2
Определим провес провода:
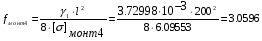 м
м
Определим натяжение провода:
Hмонт4 = монт4 F = 6.09533 493.3 = 3006.92495 кг.
5) Найдем напряжение в проводе при tмонт5 = +25C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт5= +25C
1=п=3.7299810-3
монт5 =?
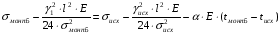
подставив значения, будем иметь:
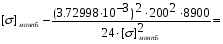
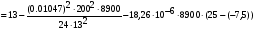
получим:
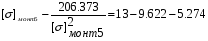
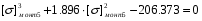
Примем: [] монт5=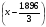 или [] монт5=x-0.632
или [] монт5=x-0.632
[] монт53x3-1.896x2+1.198x-0.252
[] монт52x2-1.264x+0.399
Подставляя в исходное уравнение, получим:
x3-1.896x2+1.198x+0,252+1,896x2-2.397x+0,757-206.373=0
получим:
x3-1.199x-205.868=0 x3-30,399x-2 102.934
p=0.399 q=102.934
p3=0.064 q2=10595.429 q2 > p3.
Получим случай №2:
Определяем угол из уравнения
ch=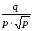 : ch = 407.8
: ch = 407.8
= 6.704, тогда x=+2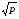 ch (/3) =1.263ch (2.235) =5.972
ch (/3) =1.263ch (2.235) =5.972
[] монт5=5.34019 кг/мм2
Определим провес провода:
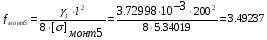 м
м
Определим натяжение провода:
Hмонт5 = монт5 F = 5.34019 493.3 = 2634.31573 кг.
6) Найдем напряжение в проводе при tмонт6 = +40C.
Исходный режим
tисх= - 7.5C
исх=0.01047
исх = [] исх = 13
Режим
tмонт6= +40C
1=п=3.7299810-3
монт6 =?
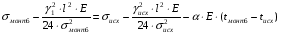
подставив значения, будем иметь:
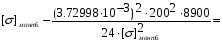
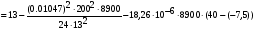
получим:
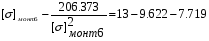
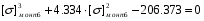
Примем: [] монт6=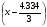 или [] монт6=x-1.445
или [] монт6=x-1.445
[] монт63x3-4.334x2+6.261x-3.015 [] монт62x2-2.889x+2.087
Подставляя в исходное уравнение, получим:
x3-4.334x2+6.261x-3,015+4,334x2-12.564x+9,045-206.373=0
получим:
x3-6.261x-200.343=0 x3-32,087x-2 100.171
p=2.087 q=100.171
p3=9.091 q2=10034.309
q2 > p3.
Получим случай №2: определяем угол из уравнения
ch=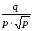 : ch = 33.222
: ch = 33.222
= 4.196, тогда x=+2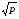 ch (/3) =2.889ch (1.399) =6.208
ch (/3) =2.889ch (1.399) =6.208
[] монт6=4.76293 кг/мм2
Определим провес провода:
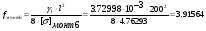 м
м
Определим натяжение провода:
Hмонт6 = монт6 F = 4.76293 493.3 = 2349.55337 кг.
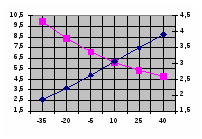
Результаты расчетов заносим в таблицу:
tмонт, C
монт, кг/мм2
fмонт, м
Hмонт, кг
-35
9,94216
1,87584
4904,46753
-20
8,36556
2,22937
4126,73075
-5
7,08739
2,63142
3496, 20949
+10
6,09553
3,0596
3006,92495
+25
5,34019
3,49237
2634,31573
+40
4,76293
3,91564
2349,55337
По этим полученным данным строим соответствующие графики монтажа провода.
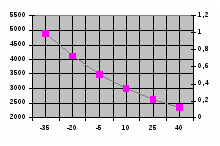
Расчет кривой провисания нити
Уравнение кривой провисания нити имеет такой вид:
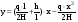
Учитывая, что: q=F и H=F, получим следующее уравнение:
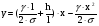
Разобьем расстояние между опорами на 20 (двадцать) равных частей:
X0
0
X11
110
X1
10
X12
120
X2
20
X13
130
X3
30
X14
140
X4
40
X15
150
X5
50
X16
160
X6
60
X17
170
X7
70
X18
180
X8
80
X19
190
X9
90
Х20
200
X10
100
Рассмотрим режимы эксплуатации:
1) Режим минимальных температур: =1=3.7299810-3 кг/ (ммм2), =9.94216 кг/ (мм2). Согласно этим данным, получим уравнение:
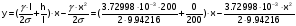
или y= 0.03752x - 0.00019x2
Расстояние
Провес, м
Расстояние
Провес, м
X0
0
X11
1.85708
X1
0.35641
X12
1.80081
X2
0.6753
X13
1.70702
X3
0.95668
X14
1.57571
X4
1.20054
X15
1.40688
X5
1.40688
X16
1.20054
X6
1.57571
X17
0.95668
X7
1.70702
X18
0.6753
X8
1.80081
X19
0.35641
X9
1.85708
X20
0
X10
1.87584
f-35=1.87584 м
По полученным данным построим кривую провисания нити:
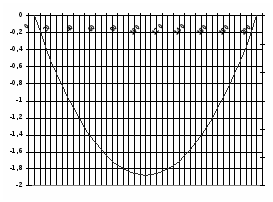
2) Режим максимальных температур: =1=3.7299810-3 кг/ (ммм2), =4.76293 кг/ (мм2). Согласно этим данным, получим уравнение:
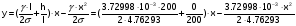
или y= 0.07831x - 0.00039x2
Расстояние
Провес, м
Расстояние
Провес, м
X0
0
X11
3.87648
X1
0.74397
X12
3.75901
X2
1.40963
X13
3.56323
X3
1.99698
X14
3.28914
X4
2.50601
X15
2.93673
X5
2.93673
X16
2.50601
X6
3.28914
X17
1.99698
X7
3.56323
X18
1.40963
X8
3.75901
X19
0.74397
X9
3.87648
X20
0
X10
3.91564
f+40=3.91564 м
По полученным данным построим кривую провисания нити:
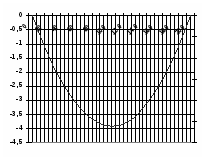
3) Режим гололеда без ветра: =3=0,01017 кг/ (ммм2), =12.77698 кг/ (мм2). Согласно этим данным, получим уравнение:
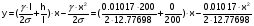
или y= 0.0796x - 0.0004x2
Расстояние
Провес, м
Расстояние
Провес, м
X0
0
X11
3.93876
X1
0.75592
X12
3.8194
X2
1.43228
X13
3.62047
X3
2.02906
X14
3.34198
X4
2.54627
X15
2.98391
X5
2.98391
X16
2.54627
X6
3.34198
X17
2.02906
X7
3.62047
X18
1.43228
X8
3.8194
X19
0.75592
X9
3.93876
X20
0
X10
3.97854
f3=3.97854 м
По полученным данным построим кривую провисания нити:
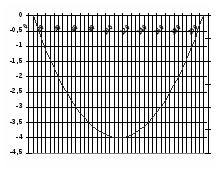
4) Режим максимальных нагрузок (гололед с ветром): =7=0,01047 кг/ (ммм2), =13 кг/ (мм2). Согласно этим данным, получим уравнение:
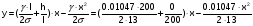
или y= 0.08054x - 0.0004x2
Расстояние
Провес, м
Расстояние
Провес, м
X0
0
X11
3.98525
X1
0.76485
X12
3.86448
X2
1.44918
X13
3.66321
X3
2.05301
X14
3.38142
X4
2.57632
X15
3.01913
X5
3.01913
X16
2.57632
X6
3.38142
X17
2.05301
X7
3.66321
X18
1.44918
X8
3.86448
X19
0.76485
X9
3.98525
X20
0
X10
4.0255
f7=4.0255 м
По полученным данным построим кривую провисания нити:
Опоры воздушных линий электропередачи
Металлические опоры воздушных линий представляют собой пространственные решетчатые конструкции, составленные из плоских ферм, соединенных между собой пространственными связями.
В данной курсовой работе для упрощения в качестве опоры будем брать пространственную ферму по форме куба или близкой к ней, с размером примерно 3 м 3 м 3м, а необходимую высоту опоры будем набирать из нескольких наслоений кубических ферм.
Внешний вид фермы и самой опоры:
3м
3м
3м
Высоту опоры Ноп определяем приближенно как параметр, состоящий из минимально допустимого расстояния от поверхности земли до провода в точке наибольшего провисания и зависящего от передаваемого напряжения и величены максимального провеса провода в вертикальной плоскости.
Величина максимального провеса провода может возникнуть только при отсутствии ветра, когда провод находится в вертикальной плоскости, проходящей через точки его крепления.
На основе всех вышеизложенных указаний, определяем высоту опоры: 8+4,0255=12,0255 12 м.
Фермы как опоры для высоковольтных линий электропередачи
Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция.
Если оси стержневой фермы лежат в одной плоскости, то ее называют плоской. Точки, в которых сходятся оси стержней, называются узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами.
верхний пояс
нижний пояс
опорная стойка
пролет фермы
раскос
стойка
Шарнирное соединение в виде треугольника:
представляет собой геометрически неизменяемую систему, а шарнирное соединение в виде четырехугольника - геометрически неизменяемая система.
Образовать геометрически неизменяемую систему с числом стержней “C” (больше трех), можно так:
a
b
c
1
2
3
4
5
К основному треугольнику “abc” последовательно присоединяем узлы, образованные двумя стержнями, оси которых не лежат на одной прямой.
Последовательность образования узлов на рисунке показана цифрами. Это - простейшая ферма. Узлы, образованные на одной прямой, имеют мгновенную изменяемость.
Если “Y” - общее число узлов, то для образования остальных (Y-3) (кроме a, b, c) необходимо по 2 стержня, т.е.: 2 (Y-3).
Общее число стержней (с учетом ab, bc, ca) будет:
C = 3 + 2 (Y + 3) = 2Y + 3.
Это - необходимое условие для получения фермы. Перенесем эту методику образования плоской фермы для образования пространственной фермы. Геометрически неизменяемые простейшие пространственные фермы могут быть образованы следующим образом.
К исходному треугольнику a-b-c (рисунок ниже) последовательно присоединяют узлы, образованные тремя стержнями, оси которых не лежат в одной плоскости. Это - простейшая пространственная ферма.
a
b
c
1
2
3
4
5
6
По способу образования узлов “Y” установим число стержней “C". Для образования первых трех узлов требуется 3 стержня, для образования остальных (Y-3) узлов требуется 3 (Y-3) стержней. Итого необходимо:
[3 (Y - 3) + 3] = (3Y - 6) = C
стержней. Условием геометрической неизменяемости свободной (т.е. незакрепленной) пространственной фермы будет:
C = 3Y - 6.
Для получения неподвижности пространственной фермы необходимы еще 6 стержней, поэтому включая в число стержней и опорные, общее число стержней для геометрически неизменяемой и неподвижной фермы будет равно:
Cф = С + 6 = 3Y.
Рассмотренные выше конструкции ферм в стержнях должны испытывать только осевые усилия, вызывающие деформации растяжения или сжатия. Это конструкции, в которых изгиб полностью уничтожен, как неприемлемый вид деформации, при котором значительная часть материала изгибаемой конструкции используется слабо.
Для образования конструкции, испытывающей только осевые усилия, необходимо соблюдение следующих условий:
соединение концов отдельных стержней должно быть шарнирным, допускающим свободное вращение (без трения) каждого стержня относительно центра шарнира; оси стержней должны проходить через центр шарнира;
внешние силы должны быть приложены только в узлах;
стержни должны быть прямолинейны, в противном случае в них возникнут изгибающие моменты. На практике идеальность шарниров достичь невозможно, т.к эти конструкции работают в атмосферной среде, где присутствует дождь, снег, способствующие возникновению ржавчины, трению в шарнирах. Поэтому в реальных конструкциях стержни соединяют наглухо (заклепки, сварка). Это есть причиной появления дополнительных усилий, не направленных вдоль осей стержней. Однако эти дополнительные усилия незначительны, и там, где оно возможно, ими пренебрегают.
Одним из основных этапов в проектировании ферм является определение усилий в стержнях, позволяющих выполнять условие прочности.
Существует несколько способов определения усилий в стержнях.
Способ вырезания узлов.
Графическое решение задачи путем построения диаграммы Максвелла-Кремоны.
Способом сечений.
Самым простым и распространенным есть способ вырезания узлов, который будет рассмотрен ниже. В процессе определения усилий может оказаться, что в отдельных стержнях загруженной фермы усилия равны нулю. Такие стержни называются нулевыми.
Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни, не производя ее расчета. Рассмотрим пространственную ферму как опору высоковольтной линии электропередачи
Лемма 1.
Если в ненагруженном узле фермы сходятся три стержня, не лежащих в одной плоскости, то усилия в каждом из этих стержней равны нулю.
x
y
z
S1
S2
S3
x = 0 S1 = 0 y = 0 S2 = 0 z = 0 S3 = 0
Лемма 2.
F
S1
S2
S3
S4
S4 = -F
Если в ненагруженном узле фермы линия действия внешней силы совпадает с осью одного стержня, то усилие в этом стержне равно по модулю внешней силе.
Лемма 3.
Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю.
S3
S4
S10
S11
F
При S3 = 0; усилия S4, F и S10 лежат в одной плоскости, кроме S11. Следовательно:
S11 = 0.
Рассмотрим определение усилий в стержнях фермы по способу вырезания узлов. Сущность этого способа состоит в том, что мысленно вырезают узлы фермы, прикладывают к ним внешние силы и реакции стержней Si и составляют уравнения равновесия сил, приложенных к рассматриваемому узлу. Вначале предполагается, что все стержни растянуты, т.е. реакции стержней Si направляют от узлов. Если в результате вычислений получают ответ со знаком минус, то соответствующий стержень сжат. Найденные реакции стержней равны по модулю внутренним усилиям в стержнях.
Последовательность рассмотрения узлов определяется, обычно, условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия сил. Для пространственной фермы - три уравнения равновесия, а, следовательно, необходимо выбирать расчетные узлы из условия, чтобы в них было не более трех неизвестных.
Определим усилия в стержнях пространственной фермы, представленной на рисунку ниже, а также реакции в опорах A5, B5, C5, D5, если на узел D1 действует горизонтальная сила F, направленная вдоль стержня A1D1. Размеры указаны на рисунке. По реакциям в опорах подобрать размеры болтов из условия прочности на срез и растяжение. Материал болта - Сталь 30, [] = 90 МПа, [] = 180 МПа. Для определения усилий в стержнях 1 - 48 фермы воспользуемся способом вырезания узлов. Будем последовательно вырезать все узлы фермы, соблюдая требования, изложенные выше.
Hmax 9.81 = F = 4904.46753 9.81 = 48112.826 Н;
M = F 2.5 = 48112.826 2.5 = 120282.065 Нм;
F = F = M / 3 = 120282.065/3 = 40094.022 Н.
Узел A1:
A1
x
y
z
S1
S5
S2
S6
Согласно лемме 2: S2 = F + H = 48112.826 + 0094.022 = = 88206.848 Н xi = 0; -S3 = 0 zi = 0; -S12 = 0
D1
x
y
z
S3
S2
S12
S2
F
H
= 0.707
sin = 1 – 0.7072 = 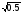 = 0.707
= 0.707
Узел C1:
C1
y
z
F
S4
S5
S3
xi = 0; S1 + S7 cos(90-) = 0 yi = 0; S4 + S9 cos = 0 zi = 0; -S8 – S7 cos – - S9 sin = 0 x S10 S11
B1
x
y
z
S7
S4
S8
S9
S1
Выполним расчеты:
S6 = S6 = 0
S2 = 88206.848 Н
S5 = - S2/cos = - 88206.848/0.707 = - 124762.16 Н
S1 = - S5 cos = 124762.16 0.707 = 88206.85 H
S3 = 0
S12 = 0
S11 = - S5 cos / sin = 124762.16 0.707/0.707 = 124762.16 H
S4 = - F - S5 cos = - 40094.022 + 124762.16 0.707 = 48112.83 H
S10 = - S11 cos = - 124762.16 0.707 = - 88206.85 H
S7 = - S1/sin = - 88206.85/0.707 = - 124762.16 H
S9 = - S4/cos = - 48112.83/0.707 = - 68052.09 H
S8 = - S7 cos - S9 sin = 124762.16 0.707 + 68052.09 0.707 =
= 88206.85 + 48112.83 = 136319.68 H
xi = 0; -S13 - S7 sin - - S17 cos = 0 yi = 0; S14 + S17 cos = 0 zi = 0; S6 – S18 + S7 cos = 0
A2
x
y
z
S7
S13
S18
S17
S6
S14
Узел D2:
D2
x
y
z
S24
S11
S12
S15
S14
xi = 0; -S15 - S11 sin = 0 yi = 0; -S14 = 0 zi = 0; S12 – S24 + S11 cos = 0
xi = 0; S15 + S17 cos + + S23 sin = 0 yi = 0; -S16 - S17 cos - - S9 cos = 0 zi = 0; S10 – S22 – S23 cos + + S9 sin = 0
y
C2
x
z
S23
S10
S22
S15
S17
S9
S16
xi = 0; S13 + S19 sin = 0 yi = 0; S16 + S21 cos = 0 zi = 0; S8 – S20 – S19 cos - - S21 sin = 0
B2
x
y
z
S19
S16
S20
S21
S8
S13
Выполним расчеты:
S14 = 0
S17 = 0
S13 = - S7 sin = 124762.16 0.707 = 88206.85 H
S18 = S7 cos = - 124762.16 0.707 = - 88206.85 H
S15 = - S11 sin = - 124762.16 0.707 = - 88206.85 H
S24 = S11 cos = 124762.16 0.707 = 88206.85 H
S23 = - S15/sin = 88206.85/0.707 = 124762.16 H
S22 = S10 - S23 cos + S9 sin = - 88206.85 - 124762.16 0.707 -
68052.09 0.707 = - 88206.85 - 88206.85 - 48112.83 =
= - 224526.53 H
S19 = - S13/sin = - 88206.85/0.707 = - 124762.16 H
S16 = - S9 cos = 68052.09 0.707 = 48112.83 H
S21 = - S16/cos = - 48112.83/0.707 = - 68052.09 H
S20 = S8 - S19 cos - S21 sin = 136319.68 + 124762.16 0.707 +
+ 68052.09 0.707 = 136319.68 + 88206.85 + 48112.83 =
= 272639.36 H
A3
x
y
z
S30
S19
S18
S25
S29
S26
xi = 0; -S25 - S19 sin - - S29 cos = 0 yi = 0; S26 + S29 cos = 0 zi = 0; S18 – S30 + S19 cos = 0
xi = 0; -S27 - S23 sin = 0 yi = 0; S26 = 0 zi = 0; S24 – S36 + S23 cos = 0
D3
x
y
z
S36
S23
S24
S27
S26
xi = 0; S27 + S35 sin + + S29 cos = 0 yi = 0; -S28 - S21 cos - - S29 cos = 0 zi = 0; S22 – S34 – S35 cos + + S21 sin = 0
C3
x
y
z
S35
S28
S34
S27
S21
S29
S22
xi = 0; S25 + S31 sin = 0 yi = 0; S28 + S33 cos = 0 zi = 0; S20 – S32 – S31 cos - - S33 sin = 0
B3
x
y
z
S31
S28
S32
S33
S20
S25
Выполним расчеты:
S26 = 0
S29 = 0
S25 = - S19 sin = 124762.16 0.707 = 88206.85 H
S30 = S18 + S19 cos = - 88206.85 - 124762.16 0.707 =
= - 176413.7 H
S27 = - S23 sin = - 124762.16 0.707 = - 88206.85 H
S36 = S24 + S23 cos = 88206.85 + 124762.16 0.707 = 176413.7 H
S35 = - S27/sin = 88206.85/0.707 = 124762.16 H
S29 = - (S27 + S35 sin) / cos = - (-88206.85 + 124762.16 0.707) /
/ 0.707 = 0
S28 = - S21 cos = 68052.09 0.707 = 48112.83 H
S34 = S22 - S35 cos + S21 sin = - 224526.53 -124762.16 0.707 -
68052.09 0.707 = - 360846.21 H
S31 = - S25/sin = - 88206.85/0.707 = - 124762.16 H
S33 = - S28/cos = - 48112.83/0.707 = - 68052.09 H
S32 = S20 - S31 cos - S33 sin = 408959.04 H
xi = 0; -S37 - S31 cos - - S41 cos = 0 yi = 0; S38 + S41 cos = 0 zi = 0; S30 – S42 + S31 cos = 0
x
y
z
Узел A4:
S42
S31
S30
S37
S41
S38
xi = 0; -S39 - S35 cos = 0 yi = 0; -S38 = 0 zi = 0; S36 – S48 + S35 cos = 0
D4
x
y
z
S48
S35
S36
S39
S38
xi = 0; S39 + S41 cos + + S47 cos = 0 yi = 0; -S40 - S33 cos - - S41 cos = 0 zi = 0; S34 – S46 + S33 cos - - S47 cos = 0
C4
x
y
z
S47
S40
S46
S39
S33
S41
S34
xi = 0; S37 + S43 cos + + S45 cos = 0 yi = 0; S40 + S45 cos = 0 zi = 0; S32 – S44 – S43 cos= 0
B4
x
y
z
S43
S40
S44
S45
S32
S37
Выполним расчеты:
S38 = 0
S39 = - S35 cos = - 124762.16 0.707 = - 88206.85 H
S41 = - S38/cos = 0/0.707 = 0
S40 = - S33 cos - S41 cos = 68052.09 0.707 = 48112.83 H
S37 = - S31 cos - S41 cos = 124762.16 0.707 = 88206.85 H
S42 = S30 + S31 cos = - 176413.7 - 124762.16 0.707 =
= - 264620.55 H
S45 = - S40/cos = - 48112.83/0.707 = - 68052.09 H
S43 = (-S37 - S45 cos) / cos = (-88206.85 + 68052.09 0.707) /
/ 0.707 = - 56710.07 H
S44 = S32 - S43 cos = 408959.04 + 56710.07 0.707 =449053.06 H
S47 = ( - S39 - S41 cos) / cos = 124762.16 H
S46 = S34 + S33 cos - S47 cos = - 497165.89 H
S48 = S36 + S35 cos = 176413.7 +124762.16 0.707= 264620.55 H
A5
x
y
z
S43
S42
zA5
XA5
yA5
xi = 0; xA5 - S43 cos = 0 yi = 0; yA5 = 0 zi = 0; zA5 + S42 + S43 cos = 0
xi = 0; xD5 - S47 cos = 0 yi = 0; yD5 = 0 zi = 0; zD5 + S48 + S47 cos = 0
D5
x
y
z
S47
S48
zD5
XD5
yD5
xi = 0; xC5 = 0 yi = 0; yC5 - S45 cos = 0 zi = 0; zC5 + S46 + S45 cos = 0
C5
x
y
z
S45
S46
zC5
XC5
yC5
xi = 0; xB5 = 0 yi = 0; yB5 = 0 zi = 0; zB5 + S44 = 0
B5
x
y
z
S44
zB5
yB5
Выполним расчеты:
xA5 = S43 cos = - 56710.07 0.707 = - 40094.02 H, yA5 = 0
zA5 = - S42 - S43 cos = 264620.55 +56710.07 0.707 = 304714.57 H
xD5 = S47 cos = 124762.16 0.707 = 88206.85 H
yD5 = 0
zD5 = - S48 - S47 cos = - 264620.55 - 124762.16 0.707 =
= - 352827.4 H
xC5 = 0
yC5 = S45 cos = - 68052.09 0.707 = - 48112.83 H
zC5 = - S46 - S45 cos = 497165.89 + 68052.09 0.707 =
= 545278.72 H
xB5 = 0
yB5 = 0
zB5 = S44 = S44 = 449053.06 H
Определим реакции в опорах:
RA5 = x2A5 + y2A5 + z2A5 = 307341.02 H
RD5 = x2D5 + y2D5 + z2D5 = 363686.16 H
RC5 = x2C5 + y2C5 + z2C5 = 547397.23 H
RB5 = x2B5 + y2B5 + z2B5 = 449053.06 H
Из всего вышеуказанного видно, что все опоры являются нагруженными - и эти нагрузки довольно большие, т.к мы имеем тяжелый исходный провод и большой пролет.
Теперь из проверки на срез и растяжение болтов в опорах подберем его минимально допустимый диаметр.
[] т = 240 МПа
[] = 60 МПа
[] раст = 0.6 [] т = 144 МПа
Для опоры A5:
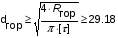
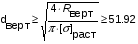
Для опоры D5:
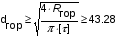
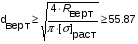
Для опоры C5:
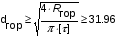
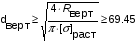
Для опоры B5:
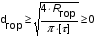
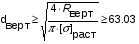
Использованная литература
1.Кореняко О.С. и другие “Курсовое проектирование по теории машин и механизмов".
2.Методические указания “Задание на курсовой проект по курсу “Прикладная механика””.
3.Методические указания “Практические занятия по курсу “Прикладная механика”".
4.Яблонский “Сборник задач по теоретической механике”.
Задание на курсовую работу
Дать анализ эксплуатации воздушной линии электропередачи в режимах эксплуатации I, IIа, IIб, максимальных температур (IV).
Установить исходный режим и произвести сравнение с другими режимами.
Определить напряжение и провес провода f для различных режимов эксплуатации.
Построить монтажный график и дать анализ условиям монтажа.
Построить кривую провисания нити.
Определить положение низшей точки провисания провода.
Найти плоскость провисания провода с учетом ветровой нагрузки.
Определить высоту опоры.
Определить усилие в стержнях фермы.
Определить реакции в местах крепления опоры и подобрать диаметр болта крепления опоры, рассматривая деформацию на срез и растяжение.
Варианты на курсовую работу
Общий вариант - № 8
Напряжение U
5
Местность M
1
Материал провода Pr
3
t установки провода
4
Перепад высот h
6
t гололеда
10
Скоростной напор ветра Q
2
tmax
5
tmin
8
Расстояние между точками подвеса l1
7
Толщина корки льда c
8

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ