Рассеяние рентгеновских лучей на молекулах фуллерена
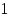
 МОУ СОШ №21
МОУ СОШ №21
Реферат по физике
на тему:
«РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
НА МОЛЕКУЛАХ ФУЛЛЕРЕНА»
Работу выполнил
ученик 11 «Г» класса
Лыков Владимир Андреевич
Преподаватель:
Харитонова Ольга Александровна
Нижний Новгород
2008
Содержание
Цели работы
1. Компьютерное моделирование рассеяния рентгеновских лучей на молекулах фуллерена и фрагментах кристаллов фуллеритов.
2. Исследование поворотной псевдосимметрии углового распределения интенсивности рассеянных рентгеновских лучей.
2. Теоретическая часть
2.1. Колебания
2.1.1. Одномерные колебательные движения
Рассмотрим одномерное периодическое движение материальной точки. Периодичность движения означает, что координата точки x является периодической функцией времени t:
x = f(t). (1.1)
Иначе говоря, для любого момента времени выполняется равенство
f(t + T) = f(t), (1.2)
где постоянная величина Т называется периодом колебания.
Существенно, что координата может быть не только декартовой, но и углом и т.д.
Существует множество разновидностей периодического движения. Например, таковым является равномерное движение материальной точки по окружности.
х
т
mg
Важным типом периодических движений являются колебания, в которых материальная точка за период T дважды проходит положение равновесия, отклоняясь от него в разные стороны.
Рис.1.1. Шарик, подвешенный на пружине.
Характерные примеры физических систем, совершающих колебательные движения, приведены на рисунках 1.1. – 1.6. Следует заметить, что в примерах на рис.1.1, 1.2. и 1.4. тела совершают колебания вдоль прямых линий. В примере 1.5. одномерные колебания совершает поверхность жидкости в трубке (или маленькая частица, плавающая на х
т
поверхности жидкости).
т
mg
α
l
Рис.1.2. Брусок с пружиной на гладком столе пружине.
х
Рис.1.3. Шарик, подвешенный на нити.
Рис.1.4. Поплавок на поверхности жидкости.
x
L
C
q
Рис.1.5. U-образная трубка с жидкостью.
Рис.1.6. Электрический контур, содержащий конденсатор с емкостью C и катушку с индуктивностью L.
В примере 1.3. периодически меняется угол отклонения. Наконец, в примере 1.6. периодически изменяется заряд конденсатора и сила тока в катушке. Тем не менее, все эти физические процессы описываются одинаковыми математическими функциями.
2.1.2. гармонические колебания
Наиболее простой разновидностью колебаний являются гармонические. Координата материальной точки с течением времени при гармонических колебаниях изменяется по закону
x(t) =A cos(t + 0) (1.3)
где A – амплитуда смещения (максимальное смещение точки от положения равновесия), – частота, связанная с периодом соотношением
= 2 / T. (1.4)
Положением равновесия называется месторасположение материальной точки, в котором сумма действующих на нее сил равна нулю.
Аргумент косинуса t + 0 в функции (1.3) называется фазой колебания. Видно, что фаза является безразмерной величиной и линейной функцией времени. Постоянная величина 0 называется начальной фазой.
Колебания физических систем, приведенных на рис.1.1. – 1.6. совершали бы строго гармонические колебания при следующих дополнительных условиях:
Система 1.1. – при отсутствии сопротивления воздуха, система 1.2. – при отсутствии терния, система 1.3. – при малых углах и отсутствии сопротивления воздуха, системы 1.4. и 1.5. – при отсутствии вязкости жидкости, система 1.6. – при отсутствии активного сопротивления катушки и проводов.
Рассмотрим для простоты сначала одномерные гармонические колебания, когда материальная точка смещается вдоль одной прямой.
Вычислив производную функции (1.3) по времени получим скорость материальной точки:
v(t) = A sin(t+0) (1.5)
Видно, что скорость является также периодической функцией времени.
Теперь возьмем производную от функции (1.5) по времени и получим ускорение материальной точки.
a(t) = 2 A cos(t+0) (1.6)
Сравнивая функции (1.3) и (1.6) получим что координата и ускорение связанны следующим выражением
a(t) = 2 x(t),(1.7)
которое выполняется в любой момент времени.
Иначе говоря, при любых одномерных гармонических колебаниях ускорение частицы прямо пропорционально её координате, причем коэффициент пропорциональности отрицательный.
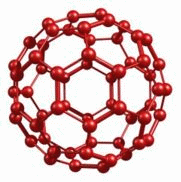
Рис.1.7. Зависимости от времени координаты (кружочки), скорости (квадратики) и ускорения (треугольники) частицы, совершающей одномерные гармонические колебания. Амплитуды А=2, период Т=5, начальная фаза 0=0.
Как известно, ускорение частицы (по основному закону динамики) прямо пропорционально силе, действующей на частицу. Следовательно, если сила прямо пропорциональна координате с обратным знаком, то частица будет совершать гармоническое колебание. Такие силы называются возвращающими.
Важным примером возвращающей силы является сила Гука (упругая сила). Таким образом, если на материальную точку действует сила Гука, то точка совершает гармонические колебания.
Так как мы рассматриваем одномерные колебания, то для анализа задачи достаточно спроецировать вектор силы Гука на ось, параллельную этой силе. Если ноль отсчета координаты x выбран в точке, в которой возвращающая сила равна нулю, то проекция силы равна
Fx = k x,(1.8)
где коэффициент k называется жесткостью.
Сравнивая уравнения (1.7) и (1.8), и используя 2-й закон Ньютона, получим важное выражение для частоты колебаний:
2 = k / m(1.9)
Это означает, что частота колебаний описывается параметрами физической системы, а не зависит от начальных условий. В частности, выражение (1.9) определяет частоту гармонических колебаний систем, показанных на рис.1.1. и 1.2.
В качестве поучительно примера рассмотрим одномерные движения, которые совершают грузы, прикрепленные к пружинам (см. рис.1.8).
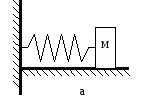
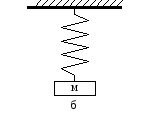
Рис.1.8. Грузы на пружинах.
Пусть массы пружин пренебрежимо малы по сравнению с массами грузов.
Грузы рассматриваются как материальные точки.
Сначала рассмотрим систему, изображенную на рис.18. а. Предположим, что первоначально груз был смещен влево и, как следствие пружина растянулась. При этом на груз (материальную точку) действуют 3 силы: сила тяжести mg, сила упругости F и сила нормальной реакции опоры N. Трением в данной задаче мы пренебрегаем (см. рис.1.9).
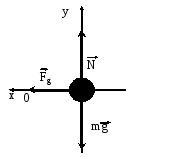
Рис.1.9. Силы на груз, лежащий на гладкой опоре, при растяжении пружины.
Запишем второй закон Ньютона для тела, изображенного на рис.1.9.
ma = mg + F + N(1.10)
Сила упругости при небольших деформациях пружин описывается законом Гука
F = – k d(1.11)
где d – вектор деформации пружины, k – коэффициент жёсткости пружины.
Заметим, что при движении груза растяжение пружины может сменяться сжатием. При этом вектор деформации d будет менять свое направление на противоположное, следовательно, то же будет происходить с силой Гука (1.11). Из этого, в частности, следует, что при начальном сжатии пружины векторное уравнение движение (1.10) будет иметь тот же вид:
ma = mg – k d + N(1.12)
Выберем начало координат в точке расположения груза при недеформированной пружине. Ось X направим горизонтально, ось Y –вертикально, т.е. перпендикулярно опоре (см. рис.1.9).
Так как груз движется вдоль опоры по горизонтали, то проекция ускорения на ось Y равна нулю. Тогда сила тяжести полностью компенсируется нормальной реакции опоры
N + mg = 0 (1.13)
Проецирование уравнения движения (1.12) на ось X дает скалярное уравнение:
ma = – kd,(1.14)
где a – горизонтальная проекция ускорения груза, d – проекция вектора деформации пружины.
Иначе говоря, ускорение направлено по горизонтальной оси X и равно
a = – (k/m) d(1.15)
Еще раз заметим, что уравнение (1.15) справедливо и при растяжении, и при сжатии пружины.
Так как начало координат выбрано так, что оно совпадает с концом недеформированной пружины, то проекция деформации совпадает со значением горизонтальной координаты груза x:
a = – (k/m) x (1.16)
По определению проекция ускорения равна второй производной соответствующей координаты по времени. Следовательно, одномерное уравнение движения (1.16) можно переписать в виде
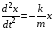 (1.17)
(1.17)
Иначе говоря, проекция ускорения прямо пропорциональна координате, причем коэффициент пропорциональности имеет отрицательный знак.
Уравнение (1.17) является дифференциальным второго порядка, общая теория решения таких уравнений изучается в курсе математического анализа. Однако легко доказать непосредственной подстановкой, что функция гармонических колебаний (1.3) удовлетворяет уравнению (1.17). Как уже было доказано ранее, частота колебаний выражается формулой (1.9).
Амплитуда A и начальная фаза 0 колебаний определяются из начальных условий.
Пусть первоначально груз был смещен вправо от положения равновесия на расстояние d0, а начальная скорость груза равна нулю. Тогда используя функции (1.3) и (1.5), запишем для момента времени t=0 следующие уравнения:
d0 =A cos(0) (1.18)
0 = A sin(0) (1. 19)
Решением системы (1.18) – (1. 19) являются следующие значения A = d0 и 0= 0.
Для других начальных условий величины A и 0, естественно приобретут другие значения.
Теперь рассмотрим систему, изображенную на рис.1.8. б. На груз в этом случае действуют только две силы: сила тяжести mg и сила упругости F (см. рис.1.10). Ясно, что в положении равновесия эти силы компенсируют друг друга, следовательно, пружина растянута.
Пусть груз несколько смещается по вертикали. Тогда векторное уравнение движение будет иметь вид, аналогичный уравнению (1.12)
ma = mg – k d(1. 20)
причем независимо от направления вертикального смещения (вверх или вниз).
Все векторы в уравнении (1. 20) направлены вертикально, поэтому это уравнение целесообразно спроецировать на вертикальную ось координат. Направим ось вниз, а начало координат выберем в точке, где тело находится в состоянии равновесия (см. рис.1.10).
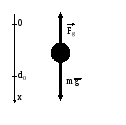
Рис.1.10. Силы, действующие груз, висящий на пружине.
Спроецировав (1.18) на ось X получим:
a = g – (k/m) d(1.21)
где a – проекция ускорения тела, d – проекция деформации пружины.
Для решения уравнения (1.21) полезно вернуться к положению равновесия груза. Уравнение Ньютона для этого положения имеет вид:
0 = g – (k/m) d0(1.22)
где d0 –деформации пружины при равновесии груза. Следовательно, вектор d0 равен
d0 = mg/k(1.23)
Видно, что в положении равновесия тела пружина действительно растянута, так как вектор d0 направлен параллельно вектору g, т.е. вниз.
Теперь поместим начало координат в точке равновесия груза на пружине, и тогда уравнение (1.21) примет вид:
a = g – (k/m) (x+ d0) (1.24)
где d0 –модуль вектора деформации пружины d0.
Подставив в уравнение (1.24) величину d0, полученную из соотношения (1.23), получим:
a = g – (k/m) (x+ (m/k) g)
или
a = – (k/m) x (1.25)
Полученное уравнение полностью совпадает с уравнением (1.16). Таким образом, тело, изображенное на рис.1.8. б, совершает также гармоническое колебательное движение, описываемое функцией (1.3), как и груз в системе, изображенной на рис.1.8. а. Частота колебаний Отличие заключается лишь в направлении колебаний (вертикальное вместо горизонтального). Но частота колебаний по-прежнему определяется жесткостью пружины и массой груза формулой (1.9).
Характерно, что начальная деформация пружины в системе на рис.1.8. б не влияет на частоту колебаний.
2.1.3. Сложение колебаний
2.1.3.1. Сложение двух гармонических колебаний с одинаковыми амплитудами и частотами
Рассмотрим пример звуковых волн, когда два источника создают волны с одинаковой амплитудами A и частотами ω. На расстоянии от источников установим чувствительную мембрану. Когда волна «пройдёт» расстояние от источника до мембраны, мембрана придёт в колебательное движение. Воздействие каждой из волн на мембрану можно описать следующими соотношениями, воспользовавшись колебательными функциями:
x1(t) = A cos(ωt + φ1),
(1.26)
x2(t) = A cos(ωt + φ2).
Для того, чтобы сосчитать колебание, с которым будет колебаться мембрана, просуммируем функции (1.26):
x(t) = x1 (t) + x2 (t) = A [cos (ωt + φ1) + cos (ωt + φ2)] (1.27)
Выражение, которое находится в скобках, можно записать иначе, воспользовавшись тригонометрической функцией суммы косинусов:
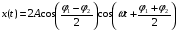 (1.28)
(1.28)
Для того чтобы упростить функцию (1.28), введём новые величины A0 и φ0, удовлетворяющие условию:
A0 = 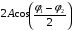 φ0 =
φ0 = 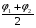 (1.29)
(1.29)
Подставим в функцию (1.28) выражения (1.29), получим
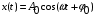 (1.30)
(1.30)
Таким образом, сумма гармонических колебаний с одинаковыми частотами ω есть гармоническое колебание той же частоты ω. При этом амплитуда суммарного колебания A0 и начальная фаза φ0 определяются соотношениями (1.29).
2.1.3.2. Сложение двух гармонических колебаний с одинаковой частотой, но разными амплитудой и начальной фазой
Теперь рассмотрим такую же ситуацию, изменив в функции (1.26) амплитуды колебаний. У функции x1 (t) заменим амплитуду A на A1, а у функции x2 (t) А на A2. Тогда функции (1.26) запишутся в следующем виде
x1 (t) = A1 cos(ωt + φ1), x2 (t) = A2 cos (ωt + φ2); (1.31)
Найдем сумму гармонических функций (1.31)
x= x1 (t) + x2 (t) = A1 cos(ωt + φ1) + A2 cos (ωt + φ2) (1.32)
Выражение (1.32) можно записать иначе, воспользовавшись тригонометрической функцией косинуса суммы:
x(t) = (A1cos(φ1) + A2cos(φ2)) cos(ωt) – (A1sin(φ1) + A2sin(φ2)) sin(ωt) (1.33)
Для того чтобы упростить функцию (1.33) введём новые величины A0 и φ0, удовлетворяющие условию:
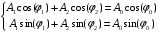 (1.34)
(1.34)
Возведём каждое уравнение системы (1.34) в квадрат и сложим полученные уравнения. Тогда мы получим следующее соотношение для числа A0:
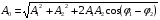 (1.35)
(1.35)
Рассмотрим выражение (1.35). Докажем, что величина под корнем не может быть отрицательной. Так как cos(φ1 – φ2) ≥ –1, значит, это единственная величина, которая может повлиять на знак числа под корнем (A12 > 0, A22 > 0 и 2A1A2 > 0 (из определения амплитуды)). Рассмотрим критический случай (косинус равен минус единице). Под корнем оказывается формула квадрата разности, что является величиной всегда положительной. Если мы начнём постепенно увеличивать косинус, то слагаемое, содержащее косинус тоже начнёт расти, тогда величина, стоящая под корнем не изменит свой знак.
Теперь рассчитаем соотношение для величины φ0, разделив второе уравнение системы (1.34) на первое и вычислив арктангенс:
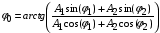 (1.36)
(1.36)
А теперь подставим в функцию (1.33) значения из системы (1.34)
x = A0(cos(φ0) cosωt – sin(φ0) sinωt) (1.37)
Преобразуя выражение, стоящее в скобках по формуле косинуса суммы, мы получим:
x(t) = A0 cos(ωt + φ0) (1.38)
И опять получилось, что сумма двух гармонических функций вида (1.31) является также гармонической функцией того же вида. Точнее говоря, сложение двух гармонических колебаний с одинаковыми частотами ω представляет собой также гармоническое колебание с той же частотой ω. При этом амплитуда результирующего колебания определяется соотношением (1.35), а начальная фаза – соотношением (1.36).
2.2. Волны
2.2.1. Распространение колебаний в материальной среде
Рассмотрим колебания в материальной среде. Одним из примеров является колебание поплавка на поверхности воды. Если в роли наблюдателя выступит птица, пролетающая над поплавком, то она заметит, что поплавок образует вокруг себя окружности, которые, что удивительно, с течением времени, удаляясь, увеличивает радиус. Но если в роли наблюдателя будет человек, стоящий на берегу, то он увидит «горбы» и «впадины», которые, чередуясь, приближаются к берегу. Это явление называют бегущей волной.
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
19
5T/4
T
3T/4
T/2
T/4
0
Для того чтобы разобраться в свойствах волны, пренебрежем сопротивлением воздуха, вязкостью воды и воздуха, т.е. диссипативными силами. Тогда механическую энергию капелек воды можно полагать сохраняющейся. В этом случае движение волны схематически можно изобразить так, как показано на рисунке 1, заменив капельки воды пронумерованными шариками. Обозначим за поплавок шарик №1.
Рис. 2.1. Схематичное изображение поперечной волны.
Мы видим, что причиной движения является шарик №1, т.е. поплавок. Он с помощью взаимодействия вовлекает в движение шарик №2, шарик №2 вовлекает №3 шарик, и т.д. Но взаимодействие между частицами происходит не мгновенно, поэтому шарик №2 будет отставать по времени. Также можно заметить, что шарик №13 колеблется так же, как и №1. Тогда можно сделать вывод, что шарик №2 будет отставать от №1 на 1/12 периода.
Отсюда периодом волны(T) можно назвать период колебаний шарика №1, амплитудой волны(A) – максимальное отклонение шарика от горизонтальной оси, а длиной волны (λ) – минимальное расстояние между максимумами ближайших горбов или минимумами ближайших впадин.
В ранее рассмотренном примере волна распространялась перпендикулярно колебаниям источника, иначе говоря, была рассмотрена поперечная волна.
Продольные волны – волны, распространяющиеся параллельно движению источника. Если рассматривать продольные волны схематически (рис.2.2), то можно заметить, что с течением времени источник колебаний (шар №1) колеблется влево-вправо и вовлекает в такое же колебательное движение остальные частички. Тогда, для продольной волны, определение периода волны, описанное выше, останется неизменным, а определения длины волны и амплитуды будут выглядеть иначе. Обобщенные понятия будут выглядеть так: длина волны – минимальное расстояние между шариками, двигающихся с одинаковыми фазами; амплитуда волны – максимальное отклонение от положения равновесия.
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
1
2
3
4
5
10
11
6
7
8
9
12
13
14
15
16
17
18
0
T/4
T/2
3T/4
T
5T/4
Рис. 2.2. Схема формирования продольной волны.
2.2.2. Волновая функция
Рассмотрим источник, совершающий гармонические колебания в материальной среде с частотой . Тогда его движение описывается функцией вида [Acos(t + φ0)]. Пусть начальная фаза 0 равна нулю. Тогда координата источника является следующей функцией времени.
x = A cos(t) (2.1)
Из-за взаимодействия частицы окружающей среды вовлекаются в движения, которое также будет являться гармоническими колебаниями. Но межчастичное взаимодействие происходит не мгновенно, поэтому колебания соседних частиц будут происходить со сдвигом во времени. Из-за конечной и постоянной скорости передачи взаимодействия этот сдвиг колебаний во времени прямо пропорционален расстоянию очередной частицы от источника.
Из предыдущих примеров следует, что в результате в среде будут распространяться возмущения, называемые волновыми. В случае поверхностных волн это возмущение представляет собой отклонение частиц воды от поверхности в спокойном состоянии. В случае звуковых волн возмущением является отклонение плотности воздуха от средней плотности воздуха в спокойном состоянии. Независимо от вида волн (продольных или поперечных) это возмущение должно описываться некоторой функцией времени и координат.
В точке источника возмущение является функцией времени, совпадающей с (2.1)
(0, t) = A cos(t). (2.2)
Рассмотрим распространение гармонического возмущения в направлении, заданном осью координат 0Z. Согласно вышеизложенному, частицы материальной среды, находящиеся на расстоянии z от источника, совершают гармонические колебания с запаздыванием по времени (из-за конечной скорости распространения взаимодействия). Следовательно, возмущение в точке z и в произвольный момент времени t совпадает с возмущением в точке z = 0 источника в некоторый предыдущий момент времени t
(z, t) = (0, t) (2.3)
Скорость распространения возмущения в данной среде наглядно выражается скоростью движения горба (или впадины) у поверхностных волн или скоростью движения уплотнения (или разрежения) у звуковой волны. Эту скорость vf называют фазовой скоростью волны. Таким образом горб, впадина или любой другой вид возмущения среды пробегает расстояние z за время z/vf.
Фазовая скорость позволяет связать моменты времени t и t следующим соотношением
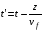 (2.4)
(2.4)
Используя соотношения (2.2) – (2.4), получим выражение для функции возмущения в следующем виде:

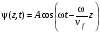 (2.5)
(2.5)
Полученное выражение называется гармонической волновой функцией или короче – гармонической волной.
В случаях однородных сред и малых возмущений фазовая скорость является постоянной величиной.
Введем новую величину, называемую волновым числом, следующим отношением:
k = ω / vf(2.6)
С помощью волнового числа гармоническая волновая функция (2.5) запишется в виде:
(z, t) = A cos(ωt – kz) (2.7)
Рассмотрим величину A. Эта величина является амплитудой волны. Как уже было сказано, амплитудой волны называется максимальное отклонение частицы от положения равновесия. Амплитуда волны может изменяться с течением времени (из-за воздействия внешних сил).
Фазой волны будет называться величина, стоящая под знаком тригонометрической функции. В зависимости от начальных условий фаза волновой функции может содержать постоянное слагаемое 0 0. Фазой волны является функцией двух аргументов времени и координаты.
Заметим, что функция (2.8) описывает волновой процесс бесконечный в пространстве и во времени.
Рассмотрим физический смысл величины k. Выберем момент времени t=0. Волновая функция (2.8) примет вид:
A cos(k z) (2.8)
Функция (2.9) может интерпретироваться как мгновенная фотография волнового процесса. Видно, что эта функция периодична в пространстве.
Согласно определению периода, следующее равенство выполняется при любых значениях координаты z
A Cos(k (z + )) = A Cos(k z)
Величина называется длиной волны. Она представляет собой минимальное расстояние между точками с одинаковой фазой (горбами, впадинами и т.п.).
Если косинусы равны, то из аргументы различаются на 2π
k (z+) = k z +2π (2.9)
Путем несложных преобразований получим следующее выражение:
λ = 2π/k(2.10)
Отсюда следует, что величина k обратно пропорциональна длине волны λ.
Рассмотрим множество точек пространства, в которых фаза волны остается равной нулю.
t – kz = 0(2.11)
Алгебраическое преобразование дает:
z/t = /k(2.12)
Отношение z/t, стоящее слева, выше было определено как фазовая скорость. Согласно (2.13), фазовая скорость плоской гармонической волны равняется
vF. = /k(2.13)
Из соотношения (2.15) также видно, что для гармонической бегущей волны в фиксированный момент времени скорость возрастания фазы на единицу длины и есть величина k (волновое число) равная
k = / vF(2.14)
Выше были рассмотрены пример гармонических волн. Но в природе такие волны встречаются очень редко. Чаще встречаются волны затухающие, т.е. волны, у которых скорость (из-за сопротивления воздуха, сил трения или других диссипативных сил) с течением времени обращается в ноль. Функции, полученные нами ранее, недействительны для затухающих волн.
Выше рассматривались волны, распространяющиеся вдоль границы раздела двух сред, и волны, распространяющиеся в объемах вещества. Например, в воздухе могут распространяться только продольные звуковые волны, а в металле и продольные, и поперечные.
Кроме того, волны можно различать по форме поверхности постоянной фазы. Важными частными случаями являются плоские и сферические волны.
2.2.3. Электромагнитные волны
Известно, что изменяющееся магнитное поле порождает электрическое. Если предположить, что меняющееся электрическое поле порождает магнитное поле, то можно предположить, как это сделал Максвелл, что из-за этого будет образовываться электромагнитная волна. И лишь потом, в 1886 году, Герцем было экспериментально доказано, что Максвелл был прав. Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стержня, разделенных искровым промежутком. Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора, то в открытом оно заполняет окружающее контур пространство, что существенно повышает интенсивность электромагнитного излучения. Колебания в такой системе поддерживаются за счет э. д. с источника, подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки. Для возбуждения электромагнитных волн вибратор Герца 8 подключался к индуктору. Когда напряжение на искровом промежутке достигало пробивного значении, возникала искра, и в вибраторе возникали свободные затухающие колебания. При исчезновении искры контур размыкался, и колебания прекращались. За тем индуктор снова заряжал конденсатор, возникала искра, и в контуре опять наблюдались колебания и т.д. Для регистрации электромагнитных волн Герц пользовался другим вибратором, имеющим такую же частоту собственных колебаний, что и излучающий вибратор, т.е. настроенным в резонанс с вибратором. Когда электромагнитные волны достигали резонатора, то в его зазоре проскакивала электрическая искра.
С помощью описанного вибратора Герц достиг частот порядка 100 МГц и получил волны, длина которых составляла примерно 3 м.П.Н. Лебедев, применяя миниатюрный вибратор из тонких платиновых стержней, получил миллиметровые электромагнитные волны с длиной волны λ = 6-4мм. Так были экспериментально открыты электромагнитные волны. Так же Герц доказал, что скорость электромагнитной волны равна скорости света:
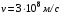 (2.15)
(2.15)
Рис. 2.3. «Моментальный снимок» системы электрических и магнитных полей.
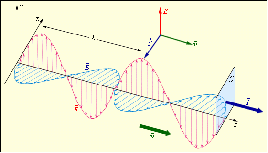
Затем было доказано, что электромагнитные волны – поперечные. Источником электромагнитных волн являются колеблющиеся заряды. В окружающем заряд пространстве возникает система электрических и магнитных полей. «Моментальный снимок» такой системы полей изображен на рис.2.3.
Качественную характеристику электромагнитных колебаний можно давать как в виде частоты колебаний, выраженной в герцах, так и в длинах волн. Чем выше частота колебаний, тем меньше длина распространяемой волны. Весь спектр этих волн условно принято делить на следующие 16 диапазонов:
Длина волны
Название
Частота
более 100 км
Низкочастотные электрические колебания
0-3 кГц
100 км - 1 мм
Радиоволны
3 кГц - 3 ТГц
100-10 км
мириаметровые (очень низкие частоты)
3 - 3-кГц
10 - 1 км
километровые (низкие частоты)
30 - 300 кГц
1 км - 100 м
гектометровые (средние частоты)
300 кГц - 3 МГц
100 - 10 м
декаметровые (высокие частоты)
3 - 30 МГц
10 - 1 м
метровые (очень высокие частоты)
30 - 300МГц
1 м - 10 см
дециметровые (ультравысокие)
300 МГц - 3 ГГц
10 - 1 см
сантиметровые (сверхвысокие)
3 - 30 ГГц
1 см - 1 мм
миллиметровые (крайне высокие)
30 - 300 ГГц
1 - 0.1 мм
децимиллиметровые (гипервысокие)
300 ГГц - 3 ТГц
2 мм - 760 нм
Инфракрасное излучение
150 ГГц - 400 ТГц
760 - 380 нм
Видимое излучение (оптический спектр)
400 - 800 ТГц
380 - 3 нм
Ультрафиолетовое излучение
800 ТГц - 100 ПГц
10 нм - 1пм
Рентгеновское излучение
30 ПГц - 300 ЭГц
<=10 пм
Гамма-излучение
>=30 ЭГц
Одним из самых распространённых видов электромагнитных волн являются световые волны. Но в нашей работе будет рассматриваться другой вид электромагнитных волн – рентгеновские лучи.
2.2.4. Рентгеновские лучи
Одним из ярких примеров электромагнитных волн, можно считать рентгеновские лучи.
В 1895 году В.К. Рентген (1845 – 1923) проводил исследования электрического тока в сильно разреженных газах. К электродам, впаянным в стеклянную трубку, из которой предварительно был выкачен воздух до давления 10–3 мм рт. ст., прикладывалась разность потенциалов в несколько киловольт. Оказалось, что при этом трубка становится источником лучей, которые Рентген назвал «икс-лучами». Основные свойства «икс-лучей» изучил сам Рентген в результате трехлетней работы, за которую в 1901 году был удостоен Нобелевской премии – первым среди физиков. Открытые им лучи впоследствии справедливо были названы рентгеновскими.
Рис.2.3. Схемы рентгеновских трубок.
а) одна из первых трубок Рентгена, б) рентгеновская трубка конца XX века.
K – термо катод, А – высоковольтный анод, T – накал термокатода, Э – пучки ускоряемых электронов (штрихпунктирные линии), Р – потоки рентгеновских лучей (штриховые линии), О – окна в корпусе трубки для выхода рентгеновских лучей.
Согласно современным научным исследованиям, рентгеновские лучи – это невидимое глазом электромагнитное излучение с длиной волны, принадлежащей диапазону с примерными границами 10–2 - 10 нанометров.
Рентгеновские лучи испускаются при торможении быстрых электронов в веществе (при этом образуют непрерывный спектр) и при переходах электронов с внешних электронных оболочек атома на внутренние (и дают линейчатый спектр).
Важнейшими свойствами рентгеновских лучей являются следующие свойства:
Лучи проходят через все материалы, в т. ч. непрозрачные для видимого света. Интенсивность проходящих лучей I уменьшается экспоненциально с толщиной x слоя вещества
I(x) = I0 exp(–/x),(2.16)
где I0 – интенсивность лучей, падающих на слой облучаемого материала.
Коэффициент характеризует ослабление потока рентгеновских лучей веществом и зависит от плотности материала и его химического состава. Многочисленные эксперименты показали, что в первом приближении наблюдается зависимость
Z4(2.17)
Потоки рентгеновских лучей проходят сквозь толстые доски, металлические листы, человеческое тело и т.д. Значительная проникающая способность рентгеновских лучей в настоящее время широко используется в дефектоскопии и медицине.
Рентгеновские лучи вызывают люминесценцию некоторых химических соединений. Например, экран, покрытый солью BaPt(CN) 4 при попадании рентгеновских лучей светится желто-зеленым цветом.
Рентгеновские лучи, попадая на фотоэмульсии, вызывают их почернение.
Рентгеновские лучи ионизируют воздух и другие газы, делая их электропроводными. Это свойство используется в детекторах, позволяющих обнаружить невидимые рентгеновские лучи и измерить их интенсивность.
Рентгеновские лучи обладают сильным физиологическим действием. Длительное облучение живых организмов интенсивными потоками рентгеновских лучей приводит к возникновению специфических заболеваний (т. н. «лучевая болезнь») и даже к летальному исходу.
Как уже было сказано ранее, рентгеновские лучи испускаются при торможении быстрых электронов в веществе и при переходах электронов с внешних электронных оболочек атома на внутренние (и дают линейчатый спектр). Детекторы, регистрирующие рентгеновские лучи базируются на свойствах рентгеновских лучей. Поэтому чаще всего в качестве детекторов используются: фотоэмульсии на пленке и пластинках, люминесцентные экраны, газонаполненные и полупроводниковые детекторы.
2.3. Дифракция волн
2.3.1. Дифракция и интерференция волн
Типичными волновыми эффектами являются явления интерференции и дифракции.
Первоначально дифракцией называлось отклонение распространения света от прямолинейного направления. Это открытие было сделано в 1665 году аббатом Франческо Гримальди и послужило основой для разработки волновой теории света. Дифракцией света представляла собой огибание светом контуров непрозрачных предметов и, как следствие этого, проникновение света в область геометрической тени.
После создания волновой теории выяснилось, что дифракция света является следствием явления интерференции волн, испущенных когерентными источниками, находящимися в различных точках пространства.
Волны называются когерентными, если разность их фаз остается постоянной с течением времени. Источниками когерентных волн являются когерентные колебания источников волн. Синусоидальные волны, частоты которых не изменяются с течением времени, являются всегда когерентными.
Когерентные волны, испущенные источниками, находящимися в различных точках, распространяются в пространстве без взаимодействия и образуют суммарное волновое поле. Строго говоря, сами волны не «складываются». Но если в какой-либо точке пространства находится регистрирующий прибор, то его чувствительный элемент будет приведен в колебательное движение под действием волн. Каждая волна действует независимо от других, и движение чувствительного элемента представляет собой сумму колебаний. Иначе говоря, в этом процессе складываются не d
L
L’
t
z
волны, а колебания, вызванные когерентными волнами.
Рис. 3.1. Система двух источников и детектора. L – расстояние от первого источника до детектора, L’ – расстояние от второго источника до детектора, d – расстояние между источниками.
В качестве базового примера рассмотрим интерференцию волн, испускаемых двумя точечными когерентными источниками (см. рис.3.1). Частоты и начальные фазы колебаний источников совпадают. Источники находятся на определенном расстоянии d друг от друга. Детектор, регистрирующий интенсивность образованного волнового поля, располагается на расстоянии L от первого источника. Вид интерференционной картины зависит от геометрических параметров источников когерентных волн, от размерности пространства, в котором распространяются волны и т.д.
Рассмотрим функции волн, которые являются следствием колебаний, испускаемых двумя точечными когерентными источниками. Для этого пустим ось z так, как показано на рис.3.1. Тогда волновые функции будут выглядеть так:
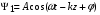
(3.1)
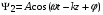
Введём понятие разности хода волн. Для этого рассмотрим расстояния от источников до регистрирующего детектора L и L’. Расстояние между первым источником и детектором L отличается от расстояния между вторым источником и детектором L’ на величину t. Для того чтобы найти t рассмотрим прямоугольный треугольник, содержащий величины t и d. Тогда можно легко найти t, воспользовавшись функцией синуса:
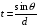 (3.2)
(3.2)
Эта величина и будет называться разностью хода волн. А теперь помножим эту величину на волновое число k и получим величину, называемую разность фаз. Обозначим её, как ∆φ
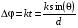 (3.3)
(3.3)
Когда две волны «дойдут» до детектора функции (3.1) примут вид:
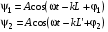 (3.4)
(3.4)
Для того чтобы упростить закон, по которому будет колебаться детектор, занулим величину (–kL + 1) в функции x1(t). Величину L’ в функции x2(t) распишем её по функции (3.4). Путем несложных преобразований получаем, что
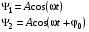 (3.5)
(3.5)
где
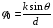 (3.6)
(3.6)
Можно заметить, что соотношения (3.3) и (3.6) одинаковы. Ранее эта величина была определена, как разность фаз. Исходя из ранее сказанного, Соотношение (3.6) можно переписать следующим образом:
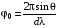 (3.7)
(3.7)
Теперь сложим функции (3.5).
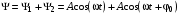 (3.8)
(3.8)
Воспользовавшись методом комплексных амплитуд, мы получим соотношение для амплитуды суммарного колебания:
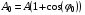 (3.9)
(3.9)
где φ0 определяется соотношением (3.3).
После того, как была найдена амплитуда суммарного колебания, можно найти интенсивность суммарного колебания, как квадрат амплитуды:
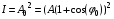 (3.10)
(3.10)
Рассмотрим график интенсивности суммарного колебания при разных параметрах. Угол θ изменяется в интервале [0; 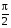 ] (это видно из рисунка 3.1), длина волны изменяется от 1 до 5.
] (это видно из рисунка 3.1), длина волны изменяется от 1 до 5.
Рис. 3.2. График зависимости интенсивности суммарногоколебания от угла φ. Длины волн берутся от 1 до 5.
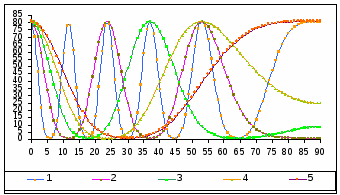 Рассмотрим частный случай, когда L>>d. Обычно такой случай встречается в экспериментах по рассеянию рентгеновских лучей. В этих экспериментах обычно детектор рассеянного излучения располагается на расстоянии много большим, чем размеры исследуемого образца. В этих случаях в детектор попадают вторичные волны, которые с достаточной точностью можно приближенно полагать плоскими. При этом волновые векторы отдельных волн вторичных волн, испущенных разными центрами рассеянного излучения, параллельны. Считается, что при этом выполняются условия дифракции Фраунгофера.
Рассмотрим частный случай, когда L>>d. Обычно такой случай встречается в экспериментах по рассеянию рентгеновских лучей. В этих экспериментах обычно детектор рассеянного излучения располагается на расстоянии много большим, чем размеры исследуемого образца. В этих случаях в детектор попадают вторичные волны, которые с достаточной точностью можно приближенно полагать плоскими. При этом волновые векторы отдельных волн вторичных волн, испущенных разными центрами рассеянного излучения, параллельны. Считается, что при этом выполняются условия дифракции Фраунгофера.
2.3.2. Дифракция рентгеновских лучей
Дифракция рентгеновских лучей - процесс, возникающий при упругом рассеянии рентгеновского излучения и состоящий в появлении отклоненных (дифрагированных) лучей, распространяющихся под определенными углами к первичному пучку. Дифракция рентгеновских лучей обусловлена пространственной когерентностью вторичных волн, которые возникают при рассеянии первичного излучения на электронах, входящих в состав атомов. В некоторых направлениях, определяемых соотношением между длиной волны излучения и межатомными расстояниями в веществе, вторичные волны складываются, находясь в одинаковой фазе, в результате чего создается интенсивный дифракционный луч. Другими словами, под действием электромагнитного поля падающей волны заряженные частицы, имеющиеся в каждом атоме, становятся источниками вторичных (рассеянных) сферических волн. Отдельные вторичные волны интерферируют между собой, образуя как усиленные, так и ослабленные пучки излучения, распространяющиеся в разных направлениях.
Можно считать, что рассеяние не сопровождается дисперсией, и, следовательно, частота рассеянных волн совпадает с частотой первичной волны. Если рассеяние является упругим, то не изменяется также и модуль волнового вектора.
Рассмотрим результат интерференции вторичных волн в точке, удаленной от всех рассеивающих центров на расстояние много большее, чем межатомные расстояния в исследуемом (облучаемом) образце. Пусть в этой точке находится детектор и складываются колебания, вызванные пришедшими в эту точку рассеянными волнами. Так как расстояние от рассеивателя до детектора значительно превышает длину волны рассеянного излучения, то участки вторичных волн, приходящих в детектор, можно с достаточной степенью точности считать плоскими, а их волновые векторы - параллельными. Таким образом, физическую картину рассеяния рентгеновских лучей по аналогии с оптикой можно назвать дифракцией Фраунгофера.
В зависимости от угла рассеяния (угла между волновым вектором первичной волны и вектором, соединяющим кристалл и детектор), амплитуда суммарного колебания будет достигать минимума или максимума. Интенсивность излучения, регистрируемая детектором, пропорциональна квадрату суммарной амплитуды. Следовательно, интенсивность зависит от направления распространения рассеянных волн, достигающих детектора, от амплитуды и длины волны первичного излучения, от числа и координат рассеивающих центров. Кроме того, амплитуда вторичной волны, образованной отдельным атомом, (а значит и суммарная интенсивность) определяется атомным фактором - убывающей функцией угла рассеяния , зависящей от электронной плотности атомов.
2.3.3. Интерференционная картина от n источников расположенных на одной прямой
Рассмотрим распределение интенсивности излучения, создаваемого n когерентными точечными источниками монохроматических волн. Геометрия системы, состоящей из n когерентных точечных источников монохроматических волн и детектора, который может перемещаться вдоль прямой линии, представлена на рис.5.1.
0
X
x
2
3
4
5
…
n
Z1
Z2
Z3
Z4
Z5
Z…
Zn
d/2
Рис.3.3. Геометрия системы n источников.
Цифрами 1,2,3,4,…,n обозначены положения точечных источников.
Ось X направлена вдоль линии перемещения детектора. Где Z1,Z2, Z3, Z4,…, Zn, – расстояния от первого, второго, третьего, …, энного источников до приёмника, вдоль оси X происходит сложение интенсивностей колебаний, L – расстояние от оси X до линии соединяющей источники.
Для того чтобы найти интенсивность n источников, используем соотношение (3.10). Амплитуды сложим векторным способом. Тогда для n источников функция (3.10) примет вид:
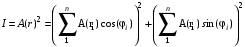 (3.11)
(3.11)
Это уравнение расчета интенсивности излучения n источников, где
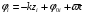 (3.12)
(3.12)
при
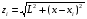 (3.13)
(3.13)
Здесь 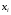 может быть вычислено следующим образом:
может быть вычислено следующим образом:
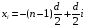 (3.14)
(3.14)
Подставив (3.12), (3.13) и (3.14) в (3.11) получим:
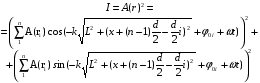 (3.15)
(3.15)
2.3.4. Атомный фактор
Атомным фактором называется величина, характеризирующая способность изолированного атома или иона когерентно рассеивать рентгеновское излучение, электроны или нейтроны (соответственно различают рентгеновский, электронный или нейтронный атомный фактор). Атомный фактор определяет интенсивность излучения, рассеянного атомом в определенном направлении.
Рассмотрим взаимодействие рентгеновской волны с отдельным атомом. Электрическое поле волны порождает периодические силы, действующие на все заряженные частицы, входящие в состав атома – на электроны и на ядро. Ускорение, которое получает частица, обратно пропорционально массе частицы. Каждая частица становится источником вторичной (т.е. рассеянной) волны. Интенсивность излучения пропорциональна квадрату ускорения, поэтому рассеянное излучение порождается практически только электронами, поэтому рентгеновский атомный фактор зависит от распределения в атоме электронной плотности.
Электроны рассредоточены внутри атома, а размер атома соизмерим с длиной рентгеновской волны. Поэтому вторичные волны, созданные отдельными электронами атома, обладают разностью фаз. Этот фазовый сдвиг φ зависит от направления распространения рассеянной волны относительно направления волнового вектора первичной волны. Следовательно, амплитуда излучения, рассеянного атомом, зависит от угла рассеяния.
Атомный фактор f (или функция атомного рассеяния) определяется как отношение амплитуды волны, рассеянной одним атомом к амплитуде волны, рассеянной одним свободным электроном. Величина атомного фактора зависит от угла рассеяния и длины волны излучения . В качестве аргумента функции атомного фактора в рентгеноструктурных исследованиях используют величину = sin() / .
Если полярный угол = 0, то значение атомного фактора равно количеству электронов в атоме (иначе говоря, атомному номеру химического элемента в таблице Менделеева). С ростом угла рассеяния атомный фактор f() монотонно убывает до нуля. Типичный вид функции атомного рассеяния приведен на рис.3.4.
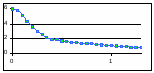
Рис.3.4
3.5. Дифракция Фраунгофера рентгеновских лучей на атомах кристалла
Пусть на кристаллический образец направлен поток рентгеновских лучей с определенной длиной волны . В физических исследованиях (при расшифровке атомной структуры рентгенодифракционным методом, рентгеноспектральном элементном анализе и т.д.) обычно реализуется геометрическая схема эксперимента со следующими геометрическими особенностями (см. рис.1).
1
2
3
Рис.3.5. Геометрическая схема облучения маленького образца узким пучком рентгеновских лучей.
1 – генератор рентгеновских лучей (например, рентгеновская трубка), 2 – коллиматор, 3 – исследуемый образец. Штриховые стрелки изображают потоки рентгеновских лучей.
С помощью коллиматора формируется узкий пучок рентгеновских лучей. Облучаемый кристаллический образец располагается от выхода из коллиматора на расстоянии значительно больше размера образца. В рентгеноструктурных исследованиях образцы подготавливаются размером меньшим поперечного сечения пучка. Как говорят, образец «купается» в пучке падающих рентгеновских лучей (см. выноску на рис.3.5).
Тогда можно с хорошей точностью полагать, на исследуемый образец падает плоская электромагнитная волна с длиной . Иначе говоря, все атомы образца подвергаются воздействию когерентных плоских волн с параллельными волновыми векторами k0.
Рентгеновские лучи представляют собой электромагнитные волны, которые являются поперечными. Если ось координат Z направить вдоль волнового вектора k0, то компоненты электрического и магнитного полей плоской электромагнитной волны могут быть записаны в следующем виде:
EX = EX0 cos(t – k0 z + 0) EY = EY0 cos(t – k0 z + 0)
(3.16)
BX = BX0 cos(t – k0 z + 0) BY = BY0 cos(t – k0 z + 0)
где t – время, – частота электромагнитного излучения, k0 – волновое число, 0 – начальная фаза. Волновое число представляет собой модуль волнового вектора и обратно пропорционально длине волны k0 = 2π/. Численное значение начальной фазы зависит от выбора начального момента времени t0=0. Величины EX0, EY0, BX0, BY0 являются амплитудами соответствующих компонент (3.16) электрического и магнитного полей волны.
Таким образом, все компоненты (3.16) плоской электромагнитной волны описываются элементарными гармоническими функциями вида:
= A0 cos(t – kz+ 0) (3.17)
Рассмотрим рассеяние плоской монохроматической рентгеновской волны на множестве атомов исследуемого образца (на молекуле, кристалле конечных размеров и т.п.). Взаимодействие электромагнитной волны с электронами атомов приводит к генерированию вторичных (рассеянных) электромагнитных волн. Согласно классической электродинамике, рассеяние на отдельном электроне происходит в телесный угол 4 и обладает существенной анизотропией. Если первичное рентгеновское излучение не поляризовано, то плотность потока рассеянного излучение волны описывается следующей функцией
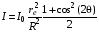 (3.18)
(3.18)
где I0 – плотность потока первичного излучения, R – расстояние от точки рассеяния до места регистрации рассеянного излучения, – полярный угла рассеяния, который отсчитывается от направления волнового вектора плоской первичной волны k0 (см. рис.3.6). Параметр
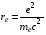 2,818106 нм(3. 19)
2,818106 нм(3. 19)
исторически называется классическим радиусом электрона.
k0
Cr
Рис.3.6. Полярный угол рассеяния плоской первичной волны на маленьком исследуемом образце Cr.
Определенный угол задает в пространстве коническую поверхность. Коррелированное движение электронов внутри атома усложняет анизотропию рассеянного излучения. Амплитуда рентгеновской волны, рассеянной атомом выражается с помощью функцией длины волны и полярного угла f(, ), которая называется атомной амплитудой.
Таким образом, угловое распределение интенсивности рентгеновской волны, рассеянной атомом, выражается формулой
I = 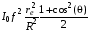 (3. 20)
(3. 20)
и обладает аксиальной симметрией относительно направления волнового вектора первичной волны k0. Квадрат атомной амплитуды f 2 принято называть атомным фактором.
Как правило, в экспериментальных установках для рентгеноструктурных и рентгеноспектральных исследований детектор рассеянных рентгеновских лучей располагается на расстоянии R значительно превышающем размеры рассеивающего образца. В таких случаях входное окно детектора вырезает из поверхности постоянной фазы рассеянной волны элемент, который, можно с высокой точностью полагать плоским.
k0
1
2
Рис.3.8. Геометрическая схема рассеяния рентгеновских лучей на атомах образца 1 в условиях дифракции Фраунгофера.
2 – детектор рентгеновских лучей, k0 – волновой вектор первичной рентгеновской волны, штриховые стрелки изображают потоки первичных рентгеновских лучей, штрих-пунктирные – потоки рассеянных рентгеновских лучей. Кружками обозначены атомы исследуемого образца.
Кроме того, расстояния между соседними атомами облучаемого образца на несколько порядков меньше диаметра входного окна детектора.
Следовательно, в данной геометрии регистрации детектор воспринимает поток плоских волн, рассеянных отдельными атомами, причем волновые векторы всех рассеянных волн можно с высокой точностью полагать параллельными.
Вышеперечисленные особенности рассеяния рентгеновских лучей и их регистрации исторически получили название дифракции Фраунгофера. Эта приближенное описание процесса рассеяния рентгеновских лучей на атомных структурах позволяет рассчитать дифракционную картину (угловое распределение интенсивности рассеянного излучения) с высокой точностью. Доказательством служит то, что приближение дифракции Фраунгофера лежит в основе рентгеноструктурных методов исследования вещества, которые позволяют определять параметры элементарных ячейках кристаллов вычислять координаты атомов, устанавливать наличие различных фаз в образце, определять характеристики дефектности кристаллов и т.д.
Рассмотрим кристаллический образец небольшого размера, содержащий конечное количество N атомов с определенным химическим номером.
Введем прямоугольную систему координат. Ее начало совместим с центром одного из атомов. Положение каждого центра атома (центра рассеяния) задается тремя координатами. xj, yj, zj, где j – порядковый номер атома.
Пусть исследуемый образец подвергается воздействию плоской первичной рентгеновской волны с волновым вектором k0, направленным параллельно оси Oz выбранной системы координат. При этом первичная волна представляется функцией вида (3.17).
Рассеяние рентгеновских лучей на атомах может быть как неупругим, так и упругим. Упругое рассеяние происходит без изменения длины волны рентгеновского излучения. При неупругом рассеянии длина волны излучения увеличивается, а вторичные волны являются некогерентными. Далее рассматривается лишь упругое рассеяние рентгеновских лучей на атомах.
Обозначим L – расстояние от начала координат до детектора. Положим, что выполняются условия дифракции Фраунгофера. Это, в частности, означает, что максимальное расстояние между атомами облучаемого образца на несколько порядков меньше, чем расстояние L. При этом чувствительный элемент детектора подвергается воздействию плоских волн с параллельными волновыми векторами k. Модули всех векторов равны модулю волнового вектора k0 = 2π/.
Каждая плоская волна вызывает гармоническое колебание с частотой
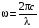 (3.21)
(3.21)
Если первичная волна удовлетворительно аппроксимируется плоской гармонической, то все вторичные (рассеянные атомами) волны являются когерентными. Разность фаз рассеянных волн зависит от разности хода этих волн.
Проведем из начала координат в точку расположения входного окна детектора вспомогательную ось Or. Тогда каждую вторичную, распространяющуюся в направлении этой оси можно описать функцией
= A1 f cos(t – kr+ 0) (3.22)
где амплитуда A1 зависит от амплитуды первичной волны A0, а начальная фаза 0 одинакова для всех вторичных волн.
Вторичная волна, испущенная атомом, находящимся в начале координат, создаст колебание чувствительного элемента детектора, описываемое функцией
A1 f() cos(t – kL+ 0) (3.23)
Другие вторичные волны создадут колебания с той же частотой (3.21), но отличающиеся от функции (3.23) сдвигом фазы, который в свою очередь, зависит от разности хода вторичных волн.
Для системы плоских когерентных монохроматических волн, движущиеся в определенном направлении, относительный сдвиг фаз прямо пропорционален разности хода L
= kL(3.24)
где k – волновое число
k = 2π/. (3.25)
Для расчета разности хода вторичных волн (3.23) сначала предположим, что облучаемый образец представляет собой одномерную цепочку атомов, расположенных вдоль оси координат Ox (см. рис.3.9). Координаты атомов заданы числами xi, (j = 0, 1, …, N–1), где x0 = 0. Поверхность постоянной фазы первичной плоской волны параллельна цепочке атомов, а волновой вектор k0 – перпендикулярен ей.
Будем рассчитывать плоскую дифракционную картину, т.е. угловое распределение интенсивности рассеянного излучения в плоскости, изображенной на рис.3.9. В этом случае, ориентация месторасположения детектора (иначе говоря, направление вспомогательной оси Or) задается углом рассеяния, который отсчитывается от оси Oz, т.е. от направления волнового вектора k0 первичной волны.
Ox
Or
O
Oz
x1
xj
k0
k
направление на детектор
Рис.3.9. Геометрическая схема дифракции Фраунгофера в заданной плоскости на прямолинейной цепочке атомов
Без потери общности рассуждений можно полагать, что все атомы расположены на правой полуоси Ox. (кроме атома находящегося в центре координат).
Так как выполнены условия дифракции Фраунгофера, то волновые векторы всех волн, рассеянных атомами, приходят во входное окно детектора с параллельными волновыми векторами k.
Из рис.3.9 следует, что волна, испущенная атомом с координатой xi проходит расстояние до детектора L – xi sin(). Следовательно, колебание чувствительного элемента детектора, вызванного вторичной волной, испущенной атомом с координатой xi, описывается функцией
A1 f() cos(t – k(L– xj sin()) + 0) (3.26)
Аналогичный вид имеют остальные рассеянные волны, попадающие в окно детектора, находящегося в заданном положении.
Величина начальной фазы 0 определяется, в сущности, моментом начала отсчета времени. Ничто не мешает выбрать величину 0 равным –kL. Тогда движение чувствительного элемента детектора, представится суммой
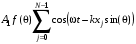 (3.27)
(3.27)
Это означает, что разность хода волн, рассеянных атомами с координатами xi и x0 составляет –xi sin(), а соответствующая разность фаз равна k xi sin().
Частота колебаний электромагнитных волн рентгеновского диапазона очень велика. Для рентгеновских лучей с длиной волны = Å частота по порядку величины составляет 1019 сек1. Современная аппаратура не может измерить мгновенные значения напряженностей электрического и магнитного полей (1) при столь быстрых изменениях полей, поэтому все детекторы рентгеновского излучения регистрируют среднее значение квадрата амплитуды электромагнитных колебаний.
Регистрируемая интенсивность рентгеновских лучей, рассеянных атомами облучаемого образца, представляет собой квадрат амплитуды суммарного колебания (11). Для вычисления этой величины целесообразно воспользоваться методом комплексных амплитуд. Каждое слагаемое суммы (11) запишем в комплексной форме
A1 f exp [i(t – j)] (3.28)
где i – мнимая единица, j – сдвиг фазы, равный в рассматриваемой физической картине kxj sin().
Выражение (12) перепишем в виде
A1 f eit e–ij (3.29)
Сомножитель, зависящий от времени, описывает колебания электромагнитного поля с частотой . Модуль этой величины равен единице. Как следствие, комплексная амплитуда электромагнитного колебания, выраженного функцией (12) имеет вид:
A1 f exp [–ij] (3.30)
Комплексная амплитуда суммарного колебания, регистрируемого детектором равна сумме величин (3.30), причем суммирование проводится по всем центрам рассеяния – т.е. по всем атомам облучаемого образца. Квадрат реальной части указанной суммы определяет регистрируемую интенсивность рассеянного рентгеновского излучения
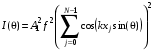 (3.31)
(3.31)
с точностью до аппаратурного коэффициента (сомножителя, определяемого характеристиками регистрирующей аппаратуры).
Интенсивность (3.31) является функцией полярного угла и описывает в плоскости xoz угловое распределение рентгеновских лучей, рассеянных цепочкой атомов, расположенных вдоль оси ox.
Теперь рассмотрим рассеяние рентгеновских лучей на конечном множестве атомов, находящихся в одной плоскости. Пусть на эту систему атомов падает плоская рентгеновская волна с волновым вектором k0, перпендикулярным плоскости атомов.
Свяжем с данной физической системой оси декартовых координат. Ось oz направим вдоль вектора k0, а оси ox и oY расположим в плоскости атомов. Положение каждого атома задается двумя координатами xj и yj, где j = 0, … N – 1. Пусть начало координат совмещено с центром одного из атомов, который имеет номер j = 0.
Рассмотрим рассеяние рентгеновских лучей в полупространство z > 0. При этом можно полагать, что детектор перемещается по полусфере определенного радиуса R, который много больше размера облучаемого образца. Направление на детектор в условиях дифракции Фраунгофера совпадает с волновыми векторами k рассеянных волн, приходящих во входное окно детектора. Это направление характеризуется двумя углами: полярным , который откладывается от оси oz (как на рис.3.9 и 3.10), и азимутом Ф, который отсчитывается от оси ox в плоскости xoY (см. рис.3.10). Иначе говоря, - угол между волновыми векторами первичной k0 и рассеянной k волн. Азимут Ф представляет собой угол между осью OX и проекцией вектора k на плоскость XOY.
Как и предыдущем случае одномерной цепочки атомов, амплитуда суммарного колебания, регистрируемая детектором определяется относительными сдвигами фаз когерентных волн, рассеянных отдельными атомами. Сдвиг фаз рассеянных волн связан с разностью хода соотношением (3.24), как и в выше рассмотренном случае.
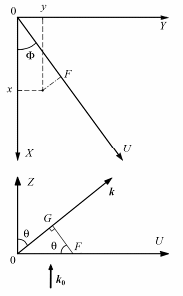
Найдем разность хода между волнами, рассеянными атомами с координатами (x0=0, y0=0) и (x, y) в направлении, заданном волновым вектором k (т.е. определенными углами и Ф). Проведем вспомогательную ось OU вдоль проекции вектора k на плоскость XOY (см. рис.3.10).
Рис.3.10. К расчету разности хода вторичных волн, рассеянных на плоской системе атомов в условиях дифракции Фраунгофера.
Точка F на оси OU – проекция центра j-го атома. Длина отрезка OF равняется x cos(Ф) + y sin(Ф), что можно получить преобразованием координат или геометрическим построением. Проекция отрезка OF на направление волнового вектора k дает искомую разность хода – длину отрезка OG, равную
l = [x cos(Ф) + y sin(Ф)] sin(). (3.32)
Следовательно, сдвиг фаз вторичных волн, рассеянными атомами с координатами (x0=0, y0=0) и (xj, yj) в направлении, заданном определенными углами и Ф, равняется
j = k [xj cos(Ф) + yj sin(Ф)] sin(). (3.33)
Регистрируемая интенсивность рассеянного рентгеновского излучения выражается формулой, аналогичной (3.31):
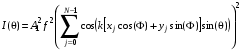 (3.34)
(3.34)
Наконец, рассмотрим дифракцию Фраунгофера рентгеновских лучей на трехмерном объекте. Воспользуемся системой декартовых координат, использованной в предыдущей задаче. Отличие физической картины от предыдущей заключается лишь в том, что центры некоторых атомов имеют координаты zj 0.
Поверхность постоянной фазы первичной плоской монохроматической волны достигает центров рассеяния с различными координатами z 0 в разные моменты времени. Как следствие, начальная фаза волны, рассеянной атомом с координатой z 0 будет отставать от фазы волны, рассеянной атомом с координатой z = 0, на величину t, где t = z / v, v – скорость распространения волны. Частота и длина волны связаны соотношением
= 2v / (3.35)
следовательно, сдвиг фазы рассеянной волны равняется 2z / или kz.
С другой стороны, если координата j-го атома zj 0, разность хода относительно «нулевой» рассеянной волны дополнительно увеличивается на величину z cos(). В результате, сдвиг фазы волны, рассеянной атомом с произвольными координатами (xj, yj, zj) в направлении, заданном углами и Ф, равен
j = k { [xj cos(Ф) + yj sin(Ф)] sin() + zj cos() zj}. (3.36)
Интенсивность рассеянных рентгеновских лучей, регистрируемая детектором, выражается следующей формулой:
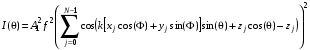 (3.37)
(3.37)
3. Практическая часть
3.1. Псевдосимметрия
3.1.1. Поворотная псевдосимметрия дифракционных картин
Симметрией называется инвариантность физической или геометрической системы по отношению к различного рода преобразованиям.
Различные типы симметрии определяются преобразованиями, относительно которых инвариантна данная система. Существует симметрия трансляционная, поворотная, симметрия подобия и т.д.
Симметрия представляет собой одно из фундаментальных свойств Вселенной. Даже основные законы физики: сохранения энергии, импульса и момента импульса связаны с определенными симметрическими преобразованиями пространственно-временного континуума.
Конкретное преобразование, относительно которого инвариантна данная система, называется операцией симметрии. Множество точек, остающихся неподвижными при симметрическом преобразовании, образуют элемент симметрии. Например, если операцией симметрии является поворот, то соответствующим элементом симметрии будет ось, вокруг которой совершается поворот.
Симметрия конечных физических систем, элементы симметрии которых пересекаются хотя бы в одной точке, называется точечной. К точечной симметрии относятся инвариантность относительно поворота на определенный угол (поворотная симметрия), инвариантность относительно отражения в определенной плоскости (зеркальная симметрия), инвариантность относительно инверсии в заданной точке (инверсионная симметрия).
Симметрия подавляющего большинства физических объектов не является абсолютной. Это означает, что физическая или геометрическая система не полностью инвариантна относительно рассматриваемого преобразования.
Для количественного описания отклонений от точной симметрии используется функционал, называемый степенью инвариантности или коэффициентом псевдосимметрии.
Пусть какая-либо физическая характеристика исследуемого объекта описывается функцией точки 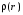 . Этой функцией может быть массовая плотность, температура электрический потенциал, плотность электрического заряда и т.д. Нас симметрия данного объекта относительно преобразования, которое задано некоторой операцией
. Этой функцией может быть массовая плотность, температура электрический потенциал, плотность электрического заряда и т.д. Нас симметрия данного объекта относительно преобразования, которое задано некоторой операцией 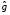 . Тогда степень инвариантности определяется следующей формулой (4.1), где V – объем объекта. Под интегралом в числителе находится произведение функции
. Тогда степень инвариантности определяется следующей формулой (4.1), где V – объем объекта. Под интегралом в числителе находится произведение функции 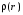 на функцию того же объекта, подвергнутого преобразованию
на функцию того же объекта, подвергнутого преобразованию 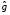 . Числитель называется сверткой функции
. Числитель называется сверткой функции 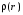 относительно операции
относительно операции 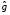 . В знаменателе стоит определенный интеграл по объему объекта от квадрата функции
. В знаменателе стоит определенный интеграл по объему объекта от квадрата функции 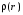 .
.
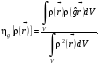 (4.1)
(4.1)
Знаменатель формулы (4.1) служит нормировкой, поэтому величина функционала 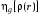 может изменяться от 0 до 1. Если рассматриваемая физическая система полностью инвариантна относительно операции
может изменяться от 0 до 1. Если рассматриваемая физическая система полностью инвариантна относительно операции 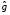 , то коэффициент псевдосимметрии равен единице. Значение
, то коэффициент псевдосимметрии равен единице. Значение 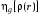 = 0 соответствует случаю, когда симметрия системы относительно операции
= 0 соответствует случаю, когда симметрия системы относительно операции 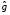 полностью отсутствует.
полностью отсутствует.
Понятие степени инвариантности можно распространить и на описание симметрии углового распределения интенсивности рассеянных рентгеновских лучей. В первую очередь, нас интересует инвариантность дифракционных картин относительно поворота на определенный азимутальный угол вокруг точки, соответствующей полярному углу = 0. Иначе говоря, целью исследования является поворотная симметрия углового распределения интенсивности рассеянных рентгеновских лучей, причем поворот осуществляется вокруг волнового вектора k0 первичного излучения.
Для изучения особенностей поворотной симметрии дифракционных картин можно адаптировать функционал общего вида (1). Исследуемой функцией в данном случае является угловое распределение интенсивности рассеянных рентгеновских лучей I(, Ф), а операцией симметрии – поворот дифракционной картины на азимутальный угол вокруг центральной точки картины с полярным углом = 0. Таким образом, количественной характеристикой поворотной симметрии дифракционной картины является следующий функционал:
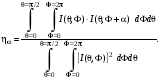 (4.2)
(4.2)
Внутренние интегралы берутся по диапазону азимутального угла Ф [0, 2π], а внешние интегралы по диапазону полярного угла [0, π/2].
Следует обратить внимание на некоторые важные особенности всех дифракционных картин. На рис.4.1. видно, что в центре полярной диаграммы находится центральный максимум интенсивности рассеянного излучения. Этот максимум имеет высокую симметрию, близкую к симметрии предельной группы С. В угловом распределении рассеянного излучения центральный максимум занимает некоторый интервал полярных углов [0, C]. Полуширина центрального максимума существенно зависит от длины волны рентгеновских лучей и количества рассеивающих атомов.
Также весьма важно, что интенсивность центрального максимума значительно превышает интенсивность всех остальных точек двумерного угловом распределении рассеянного рентгеновского излучения. Напротив, с ростом полярного угла интенсивность рассеянного излучения в среднем резко падает. Это означает, что периферийная область дифракционной картины (область полярных углов превышающих некоторое значение M) практически не влияет на величину коэффициента поворотной псевдосимметрии (4.2).
Как следствие, в степень инвариантности (4.2) основной вклад дает центральный максимум. Иначе говоря, высокая симметрия центрального максимума подавляет симметрийные особенности всех остальных характерных особенностей дифракционной картины.
Для детального исследования поворотной псевдосимметрии угловом распределении рассеянного рентгеновского излучения целесообразно вычислять функционалы следующего вида:
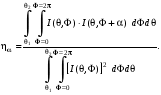 (4.3)
(4.3)
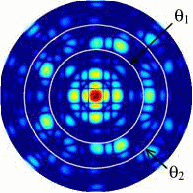
Внешние интегралы по полярному углу имеют пределы, которые может задавать исследователь, что позволяет изучать поворотную псевдосимметрию в различных интервалах полярного угла. Иначе говоря, величины типа (4.3) дают количественные оценки поворотной псевдосимметрии дифракционной картины внутри кольца, заданного парой полярных углов 1 и 2. (см. рис.4.1).
Естественно разбить диапазон полярных углов [0, π/2] на поддиапазоны определенной ширины = 2 1 и провести вычисления коэффициентов псевдосимметрии для всех таких поддиапазонов.
Рис.4.1. Кольцо на полярной диаграмме дифракционной картины, ограничивающее диапазон полярных углов [1, 2].
Выше было указано, что при компьютерном моделировании углового распределения интенсивности рассеянных рентгеновских лучей функция I(, Ф) представляется двумерным множеством числовых значений I(l, m) для конечных дискретных наборов углов l = l , l=1,…n; Фm = m Ф, m =1,…nФ. Следовательно, при вычислении коэффициентов псевдосимметрии по результатам расчета углового распределения интенсивности рассеянных рентгеновских лучей двойные интегралы в выражении (4.2) превращаются в двойные суммы
Если нас интересует усредненная поворотная псевдосимметрия всей дифракционной картины, то степень инвариантности следующей формулой:
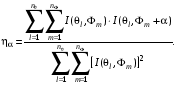 (4.4)
(4.4)
Если же мы хотим исследовать поворотную псевдосимметрию в различных поддиапазонах полярного угла (см. рис.4.1), то необходимо вычислять отношение сумм для соответствующих интервалов типа (4.3). Тогда коэффициенты псевдосимметрии представятся в виде:
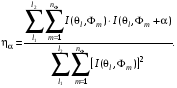 (4.5)
(4.5)
где индексы l1 и l2 соответствуют значениям полярных углов 1 и 2
1 = l1 , 2 = l2 . (4.6)
Задавая определенные значения угла поворота можно вычислять коэффициенты псевдосимметрии дифракционных картин для поворотов различных порядков. Если нас интересует поворотная псевдосимметрия n-го порядка, то угол поворота выражается соотношением.
n = 2 / n. (4.7)
Величину (4.7) далее будем называть углом поворота n-го порядка.
3.1.2. Компьютерное моделирование рассеяния рентгеновских лучей на молекулах и фрагментах кристаллических структур
В настоящей работе проводился расчет характеристик рентгеновского излучения, рассеянного конечным множеством атомов в условиях дифракции Фраунгофера. Первичное рентгеновское излучение представлялось плоской монохроматической волной с определенным волновым вектором k0 и длиной волны .
Угловое распределение интенсивности рентгеновских лучей, рассеянных на конечном множестве атомов, представляется функцией I(, Ф), зависящей от двух углов – полярного и азимутального Ф. Углы и Ф определяют направление на детектор рассеянных рентгеновских лучей, которое в условиях дифракции Фраунгофера совпадает с волновым вектором k рассеянной рентгеновской волны.
Полярный угол отсчитывается от направления волнового вектора k0 первичной рентгеновской волны. Азимутальный угол Ф откладывается в плоскости, перпендикулярной вектору k0. Азимут Ф представляет собой угол между проекцией волнового вектора k рассеянной волны на эту плоскость и произвольно выбранной азимутальной оси.
Набор значений функции I(, Ф) для всевозможных значений аргументов и Ф часто называется дифракционной картиной.
В нашей задаче рассматривается рассеяние рентгеновских лучей в «переднюю» полусферу. Следовательно, полярный угол принадлежит диапазону [0, π/2],. Азимутальный угол Ф принимает значения в интервале [0, 2π).
В качестве рассеивателей рассматривались молекулы и небольшие фрагменты кристаллов, т.е. трансляционно упорядоченных атомных структур. Месторасположение всех атомов задавалось с помощью декартовой системы координат, ось Z которой совмещалась по направлению с волновым вектором k0.
Так как задача решалась в рамках приближения дифракции Фраунгофера, то интенсивность рассеянного рентгеновского излучения представлялась формулой (3.37).
Алгоритм расчета углового распределения интенсивности рентгеновского излучения в условиях дифракции Фраунгофера был реализован в виде оригинальной компьютерной программы на алгоритмическом языке Object Pascal, разработанной в интегрированной среде Delphi-7.
Программа позволяет задавать значения химического номера атомов (для расчета функции атомного фактора), длины волны рентгеновских лучей.
Координаты центров атомов облучаемых объектов (т.е. рассеивателей) предварительно записывались во внешние файлы. В программе предусмотрена возможность выбора облучаемого объекта из заданного набора рассеивателей.
Так как в качестве рассеивающих объектов используются как молекулы, так и фрагменты кристаллов, то входными параметрами программы также являются кристаллохимические радиусы атомов и радиусы сферически симметричных молекул (кластеров).
Для расчета дифракционной картины диапазоны полярного и азимутального Ф углов разбиты на интервалы и Ф соответственно, количество которых задается пользователем. Для каждого интервала задано значение угла, согласно следующим формулам:
l = l ,l=1,…n, Фm = m Ф, m =1,…nФ,(4.8)
где nl и nm – количество интервалов разбиения полярного и азимутального углов соответственно.
Числа nl и nm связаны с длинами интервалов и Ф следующими соотношениями:
n = (π/2) / и nФ = 2π / (4.9)
Таким образом компьютерная программа позволяет рассчитать угловое распределение интенсивности рассеянных рентгеновских лучей в виде двумерного массива значений
Il,m = I(l, m). (4.10)
Величины и Ф определяют дискретность расчета дифракционной картины.
Аргументы функции углового распределения интенсивности рентгеновского излучения (4.10), рассеянного исследуемым образцом, т.е. значения углов l и m (l = 1, …, n; m =1,…nФ), представляют собой точки на полусфере.
Моделирующая программа визуализирует рассчитанное угловое распределение интенсивности рассеянного рентгеновского излучения Ii,j в виде двумерной (плоской) полярной диаграммы дифракционной картины. Полярный угол откладывается по радиусу от центра картины, азимутальный угол Ф – по дуге окружности против часовой стрелки.
Величина интенсивности рассеянного излучения I(l, m) представляется различным цветом и оттенками. В данной программе используются пять основных цветов: коричневый, красный, желтый, бирюзовый и синий. Коричневый цвет отвечает максимальной интенсивности излучения, темно-синий – минимальной. Переход от одного основного цвета к следующему соответствует изменению интенсивности рассеянного излучения на порядок (т.е. в 10 раз).
Все рассчитанные угловые распределения интенсивности рассеянного рентгеновского излучения нормируются на интенсивность центрального максимума.
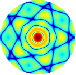
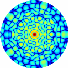
а б
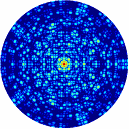
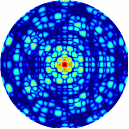
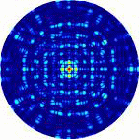
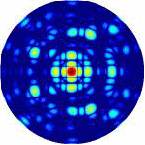
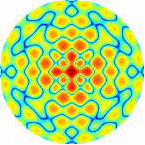
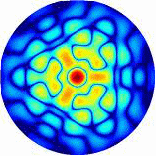
Рис.4.1. Дифракционные картины рентгеновских лучей, рассеянных молекулой фуллерена C60.
Длина волны рентгеновского излучения а) = 1,54 Å, б) = 0,71 Å.
Ось симметрии 5-го порядка молекулы C60 параллельна волновому вектору k0 первичной рентгеновской волны.
а б
Рис.4.2. Дифракционные картины рентгеновских лучей, рассеянных атомными кластерами.
а) икосаэдрический кластер, состоящий из атомов бора, ось симметрии 3-го порядка параллельна волновому вектору k0
б) остаэдрический кластер, состоящий из атомов кремния, ось симметрии 4-го порядка параллельна волновому вектору k0
Длина волны рентгеновского излучения = 0,71 Å.
На рис.4.1. – 4.2. приведены примеры полярных диаграмм углового распределения интенсивности рассеянных рентгеновских лучей для разных рассеивателей и длин волн рентгеновского излучения.
На всех полярных диаграммах углового распределения интенсивности рассеянных рентгеновских лучей в центре дифракционной картины (т.е. в окрестностях полярного угла = 0) расположен центральный дифракционный максимум, интенсивность которого пропорциональна квадрату количества атомов рассеивающего образца.
Компьютерное моделирование рассеяния рентгеновских лучей позволило установить, что поворотная симметрия дифракционной картины соответствует точечной симметрии атомного кластера. Точнее говоря, если ось симметрии n-го порядка атомного кластера параллельна волновому вектору k0 первичной рентгеновской волны, то дифракционная картина обладает поворотной симметрией n-го порядка относительно центра картины, т.е. точки с = 0.
Дифракционные картины рентгеновских лучей, рассеянных на фрагментах кристаллов, состоящих из многоатомных молекул, имеют более сложный вид. На рисунках 4.3. – 4.5. приведены некоторые характерные примеры.
аб
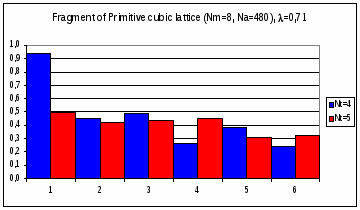
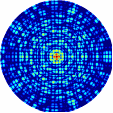
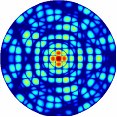
Рис.4.3. Дифракционная картина рентгеновских лучей, рассеянных фрагментом примитивной кубической решетки, содержащей в узлах молекулы фуллерена C60.
Рассеивающий фрагмент содержит 8 молекул фуллерена C60.
Длина волны рентгеновского излучения а) = 1,54 Å, б) = 0,71 Å.
Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
аб
Рис.4.4. Дифракционная картина рентгеновских лучей, рассеянных фрагментом примитивной кубической решетки, содержащей в узлах молекулы фуллерена C60.
Рассеивающий фрагмент содержит 27 молекул фуллерена C60.
Длина волны рентгеновского излучения а) = 1,54 Å, б) = 0,71 Å.
Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
…
аб
Рис.4.5. Дифракционная картина рентгеновских лучей, рассеянных фрагментом гранецентрированной кубической решетки, содержащей в узлах молекулы фуллерена C60.
Рассеивающий фрагмент содержит 14 молекул фуллерена C60.
Длина волны рентгеновского излучения а) = 1,54 Å, б) = 0,71 Å.
Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
Легко видеть, что дифракционные картины рентгеновских лучей, рассеянных фрагментами кристаллов, вообще говоря, теряют поворотную симметрию свойственную отдельным молекулам или атомным кластерам.
Для исследования симметрийных особенностей дифракционных картин типа представленных на рис.4.3. – 4.5. целесообразно использовать расчеты поворотной псевдосимметрии.
3.1.3. Псевдосимметрия дифракционных картин рассеяния рентгеновских лучей на фрагментах кристаллов фулеритов
Согласно методике, изложенной в предыдущем разделе, были проведены анализ степени инвариантности дифракционных картин, полученных при рассеянии рентгеновских лучей на молекулах фуллеренов С60 и на фрагментах кристаллов фулеридов.
Расчеты коэффициентов псевдосимметрии проводились отдельно для поддиапазонов полярного угла шириной = 5 (5 угловых градусов). Вычисления были сделаны для двух различных длин волн первичного рентгеновского излучения = 0,71 Å и = 1,54 Å, что соответствует характеристическим линиям К-альфа молибдена и меди.
Степень инвариантности дифракционных картин была рассчитаны, в первую очередь, для порядков поворота n = 2, 3, 4, 5; иначе говоря, для углов поворота полярной диаграммы n = 180, 120, 90, 72.
Пример полученных результатов приведен на рис.4.2.
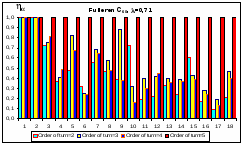
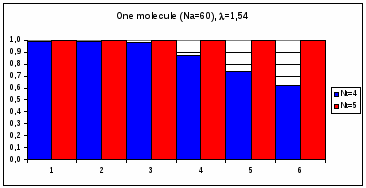
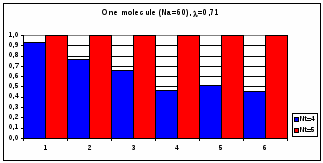
Рис.4.2. Гистограмма коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с диной волны = 0,71 на молекуле фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 5. Ось симметрии 5-го порядка молекулы C60 параллельна волновому вектору k0 первичной рентгеновской волны.
На рис.4.2. видно, что коэффициент поворотной псевдосимметрии равен единице во всех поддиапазонах полярного угла. Если порядок поворота дифракционной картины совпадает с порядком оси симметрии облучаемого объекта, вдоль которой направлен волновой вектор k0 первичной рентгеновской волны. Это характерная особенность наблюдается для атомных кластеров любой точечной симметрии.
Кристаллы фуллеридов состоят из отдельных молекул фуллеренов (рис.4.3), которые образуют трансляционно упорядоченную пространственную структуру.
Рис. 4.3. Молекула фуллерена
В настоящей работе были проведены расчеты коэффициентов поворотной псевдосимметрии дифракционных картин, формируемых при рассеянии рентгеновских лучей на небольших кубических фрагментов кристаллов, состоящих из молекул фуллеренов С60. На рис.4.4. – 4.5. приведены сравнительные гистограммы поворотной псевдосимметрии дифракционных картин для порядков поворота n = 4 и n = 5, полученных при рассеянии рентгеновских лучей на кристаллических фрагментах, содержащих различное количество молекул С60 (и следовательно, различное число атомов).
Для сравнения на рис.4.4. представлены гистограммы для одной молекулы фуллерена С60, рассчитанные при идентичных условиях и параметрах.
Рис.4.4. Гистограмма коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 0,71 Å на молекуле фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
А
б
Рис.4.5. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 0,71 Å на фрагменте кубической примитивной решетки, в узлах которой расположены молекулы фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
Число молекул фрагмента а) NМ = 8, б) NМ = 27.
а
б
Рис.4.6. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 0,71 Å на фрагменте кубической гранецентрированной решетки, в узлах которой расположены молекулы фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
Число молекул фрагмента а) NМ = 14, б) NМ = 63.
Сравнение рисунков 4.4. и 4.5, а также 4.4. и 4.6. ясно демонстрирует, что с увеличением количества молекул (и атомов) в кристаллическом фрагменте величина коэффициента поворотной псевдосимметрии 5-го порядка уменьшается во всех поддиапазонах полярного угла. Это объясняется тем, что кубические фрагменты структуры трансляционно упорядоченных молекул фуллерена не обладают поворотной симметрией 5-го порядка.
С другой стороны, на рис.4.4. 4.6. видно, что с ростом количества молекул увеличивается коэффициент поворотной псевдосимметрии 4-го порядка из-за возрастания количества рассеивающих объектов, находящихся в узлах примитивной кубической кристаллической решетки. Таким образом, в дифракционных картинах точечная симметрия кристаллической решетки превалирует над точечная симметрией отдельных атомных кластеров, расположенных в узлах решетки, даже если все кластеры имеют одинаковую ориентацию.
Указанные тенденции наблюдаются на фрагментах как примитивной, так и гранецентрированной кубической кристаллической решетки.
Далее приводятся результаты аналогичных расчетов коэффициента поворотной псевдосимметрии для длины волны рентгеновского излучения = 1,54 Å.
Рис.4.7. Гистограмма коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 1,54 Å на молекуле фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
а
б
Рис.4.8. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 1,54 Å на фрагменте кубической примитивной решетки, в узлах которой расположены молекулы фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны.
Число молекул фрагмента а) NМ = 8, б) NМ = 27.
а
б
Рис.4.9. Гистограммы коэффициентов поворотной псевдосимметрии дифракционных картин, полученных при рассеянии рентгеновских лучей с длиной волны = 0,71 Å на фрагменте кубической гранецентрированной решетки, в узлах которой расположены молекулы фуллерена С60.
По вертикали отложены значения степени инвариантности , по горизонтали – порядковые номера поддиапазонов полярного угла шириной = 15. Оси симметрии 5-го порядка молекул C60 параллельны волновому вектору k0 первичной рентгеновской волны. Число молекул фрагмента а NМ = 14, б NМ = 63.
Из сравнения рисунков 4.7-4.9. следуют те же выводы о подавлении точечной симметрии атомных кластеров точечной симметрия кристаллической решетки с возрастанием количества атомов кристаллического фрагмента (количества кластеров, расположенных в узлах кристаллической решетки). Эти выводы подтверждаются расчетами для примитивной и гранецентрированной кубической кристаллической решетки.
4. Выводы
1. Разработан алгоритм и компьютерная программа расчета углового распределения интенсивности рентгеновского излучения, рассеянного фрагментом атомной структуры в условиях дифракции Фраунгофера.
2. С помощью программы выполнены расчеты дифракционных картин, полученных при рассеянии рентгеновских лучей разных длин волн на молекулах фуллерена и фрагментах кубических структур фуллеритов.
3. Проведены исследования поворотной псевдосимметрии дифракционных картин для вышеуказанных рассеивателей. Обнаружена тенденция подавления точечной симметрии отдельных молекул симметрией кристаллической решетки.
5. Список используемой литературы
1.Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А. Кристаллография. М.: Издательство Физико-математической литературы, 2000.496 с.
2.Иванов Б.Н. Законы физики. М.: Высшая школа, 1986.335 с.
3.Иванов А.И., Минькова Р.Д., Панаиоти Н.Н. физика 9 класс. Часть I. М.: 2002.128 с.
4.Мякишев Г.Я. Синяков А.З. Физика. Колебания и волны. М.: Дрофа, 2007.287 с.
5.Потапов М.К., Александров В.В., Пасиченко П.И. Алгебра и анализ элементарных функций. Справочное пособие. М.: АО «СТОЛЕТИЕ», 1996.736 с.
6.Чупрунов Е.В., Сафьянов., Головачев В.П., Фаддеев М.А., Хохлов А.Ф. Задачи по кристаллографии. М.: Издательство Физико-математической литературы 2003. 208 с.
7.Бытько Н.Д. Физика. ч.1 и 2. М.: Высшая школа. 1972.336 с.
8.Ф. Крауфорд. Волны. 1965г.529с.
9.Горелик Г.С. Колебания и волны. М.: Государственное издательство физико-математической литературы, 1959г.572с.
6. Приложения
6.1. Приложение 1. Комплексные числа
6.1.1. Определение комплексного числа
При рассмотрении действительных чисел оказалось, что нельзя найти такое число, квадрат которого равен (–1). Для того чтобы задачи с использованием этого числа были разрешимы, вводится понятие комплексного числа.
Комплексное число представляет собой выражение вида a + bi, где a и b – действительные числа, а число i представляет собой 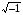 . С комплексными числами, как и с действительными, можно проводить математические операции:
. С комплексными числами, как и с действительными, можно проводить математические операции:
Выражения a + bi и c + di называют равными, только в том случае, когда одновременно выполняются два равенства a = c и b = d.
Суммой двух комплексных чисел a + bi и c + di называют комплексное число вида (a + c) + (b + d) i.
Произведением двух комплексных чисел a + bi и c + di называют комплексное число вида (ac – bd) + (ad + bc) i.
Часто комплексное число обозначают одной буквой, например.
Если комплексное число z умножить само на себя n раз (n≥2), то это произведение называют степенью комплексного числа, кроме того, z1 = z.
Раз комплексные числа можно складывать и умножать между собой, значит, среди комплексных чисел действуют и основные законы сложения и умножения: коммутативность, ассоциативность, дистрибутивность умножения относительно сложения.
Для умножения и сложения комплексных чисел существуют и обратные операции:
Разностью комплексных чисел z1 и z2 называют такое число z3, которое в сумме с z2 даёт z1.
Частным комплексных чисел z1 и z2 называют такое число z3, которое при умножении с z2 даёт z1.
Рассмотрим случай, когда одно из действительных чисел, которые составляют комплексное число a + bi равно нулю.
b = 0. Тогда комплексное число a + bi принимает вид a + 0i, что равно a.
a = 0. Тогда комплексное число принимает вид 0 + bi, что равно bi. Такие числа называют чисто мнимыми числами. Рассмотрим частный случай, когда b=1. Тогда комплексное число a + bi примет вид 0 + 1i, что равно i. Комплексное число вида 0 + 1i называют мнимой единицей.
b = 0, a = 0. Тогда комплексное число примет вид a + 0i, что равно 0.
6.1.2. Геометрическая интерпретация комплексных чисел
Всякое действительное число можно изобразить точкой на прямой. Для этого используют горизонтальную или действительную ось. Значит можно графически изобразить и чисто мнимое число. Для этого вводится вертикальная или мнимая ось. Попробуем графически изобразить комплексное число. Так как комплексное число – это сумма действительного и чисто мнимого, то комплексное число изображается так, как показано на рис.1.
a
b
i
Рис.1. Геометрическая интерпретация комплексного числа.
Комплексное число можно изобразить и радиус-вектором. Тогда, из получившегося прямоугольного треугольника, можно найти модуль этого вектора. А так как мы комплексное число изображали вектором, то модуль комплексного числа – это модуль этого радиус-вектора, или модуль комплексного числа z=a+bi – это действительное число 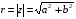 .
.
а
с
a + c
b i
d i
(b + d) i
z1
z2
z3
Рассмотрим геометрическую иллюстрацию сложения двух комплексных чисел z1 = a + bi и z2 = c + di. Изобразим комплексное число радиус-вектором. Тогда комплексные числа можно сложить по правилу параллелограмма (Рис.2).
Рис.2. Геометрическая иллюстрация суммы двух комплексных чисел.
z3 = z1 + z2 = a + bi + c + di = (a + c) + (b + d) i
Аргументом комплексного числа z = a + bi, отличного от нуля, называется любое число φ, являющихся решением системы уравнений:
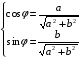 (1)
(1)
Для числа z = 0 аргумент не определяется.
Главным аргументом комплексного числа z = a + bi ≠ 0 принято называть его аргумент из интервала [0; 2π) и обозначать этот аргумент arg z.
6.1.3. Сопряженные комплексные числа
Комплексное число 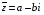 называют числом, сопряженным комплексному числу z = a + b i.
называют числом, сопряженным комплексному числу z = a + b i.
Легко видеть, что число 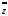 , сопряженное числу
, сопряженное числу 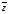 , есть число z.
, есть число z.
6.1.4. Тригонометрическая форма комплексных чисел
Пусть z=a+bi – некоторое комплексное число, отличное от нуля. Обозначим через r его модуль, а через φ - один из его аргументов. Тогда число z можно записать в виде
z = r (cos φ + i sin φ) (2)
Правая часть равенства (1) называется тригонометрической формой комплексного числа z.
6.1.5. Экспоненциальная форма комплексных чисел
Пусть z=a+bi – некоторое комплексное число, отличное от нуля. Обозначим через r его модуль, а через φ - один из его аргументов. Тогда число z можно записать в виде
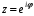 (3)
(3)
А теперь, если мы приравняем правые части соотношений (2) и (3), то мы получим формулу перехода от экспоненциальной формы к тригонометрической и наоборот:
r (cos φ + i sin φ) = eiφ(4)
Полученное соотношение называется функцией Эйлера.
6.2. Приложение 2. Определение координат вершин шестидесятигранника
Для того чтобы найти координаты шестидесятигранника, необходимо сначала рассмотреть икосаэдр. Икосаэдр имеет 12 вершин. Впишем его в сферу единичного радиуса и введём декартову систему координат. Начало системы координат совместим с центром многогранника. Ось OZ проведем через вершину P1. Ось OX выберем так, что ребро P1P2 окажется в плоскости XOZ. Тогда координаты вершины P1 равны
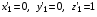 . (1)
. (1)
Для дальнейших действий необходимо получить координаты вершины P2. Для этого воспользуемся поворотом первой вершины вокруг оси Y на угол 52. Тогда искомые координаты вершины можно найти следующим образом:
x’2 = sin(252), y’2 = 0, z’2 = cos(252), (2)
Известно, что
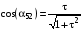 . (3)
. (3)
Путём несложных преобразований получаем, что:
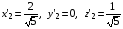 (4)
(4)
Разделим отрезок P1P2 на 3 части так, как показано на рис.1. Обрезая вершины икосаэдра на некотором расстоянии от вершины, мы получим необходимый нам шестидесятигранник. Рёбра полученного шестидесятигранника, изображают межатомные связи в молекуле фуллерена. В молекуле фуллерена существуют связи двух типов: 6-6 (это связь представляет собой общее ребро между двумя шестиугольными гранями) и 5-6 (это связь представляет собой общее ребро между шестиугольной и пятиугольной гранями). Экспериментально доказано, что длины связей различаются. Усреднённые значения равны 1,44 Å (для связи 6-6) и 1,39Å (для связи 5-6). По обозначениям на рис.1 этим значениям соответствуют следующие символы:
a ≈ 1,39Å, b ≈ 1,44 Å(5)
Найдём координаты Q1. Сначала найдём длину L отрезка P1P2. По теореме Пифагора получится:
x1
z
x
0
P1
P2
x2
z2
Q1
1
a
b
a
R2
R1
Рис.1. Ребро икосаэдра.
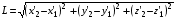 (6)
(6)
Подставив в формулу (4) значения координат (1) и (2), получим, длину отрезка P1P2:
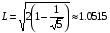 (7)
(7)
Длину отрезка P1P2 можно будет выразить следующим образом, через сумму маленьких отрезков:
L = 2a + b(8)
Для нахождения координат Q1 необходимо найти длину отрезка a. Для этого составим соотношение b к a:
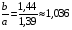 (9)
(9)
Обозначим эту величину символом S и выразим b:
b = a S(10)
А теперь подставим это соотношение в формулу (6).
L = a (2 + S) (11)
А теперь заменим L на число (5).
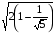 = a (2 + S) (12)
= a (2 + S) (12)
Отсюда:
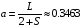 (13)
(13)
Координаты Q1 найдём, рассмотрев подобные треугольники P1P2R2 и P1Q1R1:
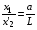 (14)
(14)
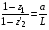 (15)
(15)
Выразим значения координат и подставим в них численные значения:
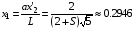 (16)
(16)
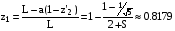 (17)
(17)
Теперь необходимо найти координаты ещё 4 точек, образованных обрезанной вершиной P1. Координаты двух из них получаются умножением полученных координат точек Q1 на матрицы поворота на углы 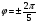 . В общем виде матрица поворота на угол выглядит так:
. В общем виде матрица поворота на угол выглядит так:
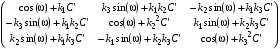 (18)
(18)
где ω – угол поворота, C’ = (1–cos(ω)), k1, k2, k3 –направляющие косинусы.
Так как мы поворачиваем вершину вокруг оси OZ, то направляющие косинусы равны k1=0, k2=0, k3=1. Тогда матрица поворота на углы 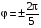 будет выглядеть следующим образом:
будет выглядеть следующим образом:
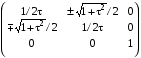 (19)
(19)
Тогда координаты точек Q2 и Q3 будут выглядеть следующим образом:
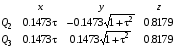 (20)
(20)
Координаты двух других точек Q4 и Q5 получаются путём умножением полученных координат точек Q1 на матрицы поворота на углы 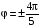 :
:
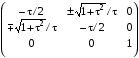 (21)
(21)
Отсюда координаты точек Q4 и Q5 будут выглядеть следующим образом:
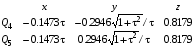 (22)
(22)
Только что были получены координаты пяти вершин, полученных обрезанием вершины P1. Для того, чтобы найти координаты 5 вершин, полученных обрезанием вершины P2 необходимо повернуть икосаэдр вокруг оси Y таким образом, чтобы вершина P1 встала на место P2 (на угол 252), а затем еще раз повернуть вокруг оси, проходящей через вершину P2 на угол . Косинус величины 52. описан в соотношении (3). Путём несложных преобразований получаем, что
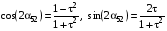 (23)
(23)
Подставим эти значения в матрицу общего вида (18). Получим
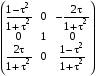 (24)
(24)
Теперь получим вторую матрицу поворота через матрицу общего вида (18). Так как мы вращаем вокруг оси, проходящей через вершину P2, то направляющие косинусы этой матрицы будут соответственно равны координатам вершины P2. Иначе
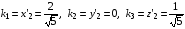 (25)
(25)
Угол поворота равен , значит
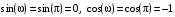 (26)
(26)
Тогда, при подставлении в матрицу (18) данных (25) и (26), получается:
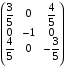 (27)
(27)
Теперь вектор с координатами вершин Q1, Q2, Q3, Q4, Q5 мы умножаем сначала на матрицу (25), а затем векторы, с полученными координатами мы умножаем на матрицу (27). Таким образом мы получаем координаты вершин Q6, Q7, Q8, Q9, Q10. Теперь каждую из полученных вершин необходимо повернуть на углы 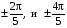 . Матрицы поворота определены, как (19) и (21). Так мы получим координаты вершин Q11 – Q30.
. Матрицы поворота определены, как (19) и (21). Так мы получим координаты вершин Q11 – Q30.
Для того чтобы получить остальные 30 вершин фуллерена надо у полученных координат Q1 – Q30 сменить знаки. Иначе говоря получить координаты вершины Q31 можно получить так:
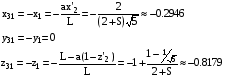 (28)
(28)
Таким же образом получаются и координаты оставшихся вершин.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ