Урок № 46-169Самоиндукция. Индуктивность. Энергия магнитного поля тока.

Самоиндукция - явление возникновения ЭДС индукции в проводящем контуре при изменении в нем силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции.

Проявление явления самоиндукции.

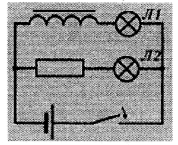Замыкание цепи. При замыкании в электрической цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое электрическое поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).

В результате Л1 загорается позже, чем Л2.

Размыкание цепи.

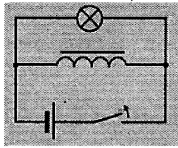При размыкании электрической цепи ток убывает, возникает уменьшение магнитного потока в катушке, возникает вихревое электрическое поле, направленное как ток (стремящееся сохранить прежнюю силу тока), т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает.

Индуктивность, или коэффициент самоиндук­ции — параметр электрической цепи, который определяет ЭДС самоиндукции, наводимой в цепи при изменении протекающего по ней тока или (и) ее деформации. Термином «индуктивность» обозначают также катушку самоиндукции, которая определяет ин­дуктивные свойства цепи.

Самоиндукция — возникновение ЭДС индук­ции в проводящем контуре при изменении в нем силы тока. ЭДС индукции возникает при изменении маг­нитного потока. Если это изменение вызывается собственным током, то говорят об ЭДС самоиндук­ции:

ε_is =–= –L,

где L — индуктивность контура, или его коэффи­циент самоиндукции.

Индуктивность — физическая величина, чис­ленно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Индуктивность можно рассчитать по формуле: Ф = L∙I, где

Ф - магнитный поток через контур, I - сила тока в контуре.

Единица индуктивности в СИ генри (Гн): [L] = [] = []= Гн; 1 Гн = 1 .

Индуктивность, как и электроемкость, зависит от геометрии проводника — его размеров и формы, но не зависит от силы тока в проводнике. Кроме того, индуктивность зависит от магнитных свойств среды, в которой находится проводник.

Индуктивность катушки зависит от:

− числа витков,

− размеров и формы катушки;

− от относительной магнитной проницаемости среды (возможен сердечник).

Токи замыкания и размыкания

При любом включении и выключении тока в цепи наблюдаются так называемые экстрато­ки самоиндукции (экстратоки замыкания и раз­мыкания), возникающие в цепи вследствие явле­ния самоиндукции и препятствующие (согласно правилу Ленца) нарастанию либо убыванию тока в цепи. Индуктивность характеризует инерционность цепи по отношению к изменению в ней тока, и ее можно рассматривать как электродинамический аналог массы тела в механике, являющейся мерой инертности тела. При этом сила тока I играет роль скорости тела.

Энергия магнитного поля тока.

Найдем энергию, которой обла­дает электрический ток в провод­нике. Согласно закону сохранения энергии энергия магнитного поля, созданного током, равна той энер­гии, которую должен затратить ис­точник тока (гальванический эле­мент, генератор на электростанции и др.) на создание тока. При прекращении тока эта энергия выделяется в той или иной форме.

Выясним, почему же для созда­ния тока необходимо затратить энергию, т. е. необходимо совершить работу. Объясняется это тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое со­здается в проводнике благодаря ис­точнику тока. Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа идет на увеличение энергии магнитного поля тока.

При размыкании цепи ток ис­чезает и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обна­руживается по мощной искре, воз­никающей при размыкании цепи с большой индуктивностью.

Записать выражение для энер­гии тока I, текущего по цепи с ин­дуктивностью L, (т. е. для энергии магнитного поля тока), можно на основании аналогии между инер­цией и самоиндукцией, о которой говорилось выше.

Если самоиндукция аналогична инерции, то индуктивность в про­цессе создания тока должна играть ту же роль, что и масса при увели­чении скорости тела в механике. Роль скорости тела в электродина­мике играет сила тока I как ве­личина, характеризующая движение электрических зарядов.

Если это так, то энергию тока W_м можно считать величиной, подобной кинетической энергии тела в ме­ханике, и записать в виде W_м = (**)

Именно такое выражение для энер­гии тока и получается в резуль­тате расчетов.

Энергия тока (**) выражена через геометрическую характеристи­ку проводника L, и силу тока в нем I. Но эту же энергию можно выра­зить и через характеристики поля. Вычисления показывают, что плотность энергии магнитного поля (т. е. энергия единицы объема) пропор­циональна квадрату магнитной ин­дукции, подобно тому, как плот­ность энергии электрического поля пропорциональна квадрату напряженности электрического поля.

Магнитное поле, созданное элек­трическим током, обладает энергией, прямо пропорциональной квадрату силы тока.

Задачи. Самоиндукция. Индуктивность.

1. Какая ЭДС самоиндукции возникает в катушке с индуктивностью 86 мГн, если ток 3,8А исчезает в ней за 0,012 с?

2. Определить ЭДС самоиндукции, если в катушке с индуктивностью 0,016 мГн сила тока уменьшается со скоростью 0,5 к А /с.

3. Какова индуктивность катушки, если при равномерном изменении в ней тока от 2 до 12 А за 0,1 с возникает ЭДС самоиндукции, равная 10 В?

4. Магнитный поток, пронизывающий контур проводника сопротивлением 0,2 Ом, равномерно изменяется с 1,2∙10^-3 Вб до 0,4∙10^-3 Вб за 2 мс. Определить силу тока в контуре.

5. В катушку сопротивлением 2 Ом течёт ток 3 А. Индуктивность катушки 50 мГн. Каким будет напряжение на зажимах катушки, если ток в ней равномерно возрастает со скоростью 200 ?

6. Какова скорость изменения силы тока в обмотке реле с индуктивностью 3,5 Гн, если в ней возбуждается ЭДС самоиндукции 105 В?

7. Катушку с ничтожно малым сопротивлением и индуктивностью 3 Гн присоединяют к источнику тока с ЭДС 15 В и ничтожно малым внутренним сопротивлением. Через какой промежуток времени сила тока в катушке достигнет 50А?

8. Катушка индуктивностью 0,2 Гн подключена к источнику тока с ЭДС =10 В и внутренним сопротивление 0,4 Ом. Определить общую ЭДС в момент размыкания цепи, если ток в ней исчезает за 0,04 с, а сопротивление проволоки катушки 1,6 Ом.

9. Катушка сопротивлением 10 Ом и индуктивностью 0,01 Гн находится в переменном магнитном поле. Когда создаваемый этим полем магнитный поток увеличился на 0,01 Вб, ток в катушке возрос на 0,5 А. Какой заряд прошёл за это время по катушке?

Урок № 46-169 Самоиндукция. Индуктивность. Энергия магнитного поля тока. Д/з:§15; § 16 [3]

1. Самоиндукция – явление возникновения ЭДС в проводящем контуре при изменении в нем силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции.

По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока, т.е. вихревое поле препятствует нарастанию тока. А в момент умень­шения тока вихревое поле поддерживает его.

Явление самоиндукции можно наблюдать в простых опытах.

С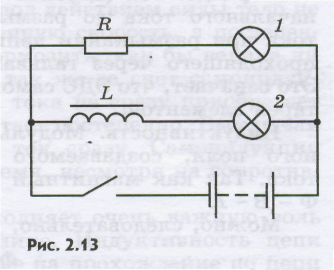хема параллельного со­единения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последователь­но с катушкой L, снабженной железным сердечником.

П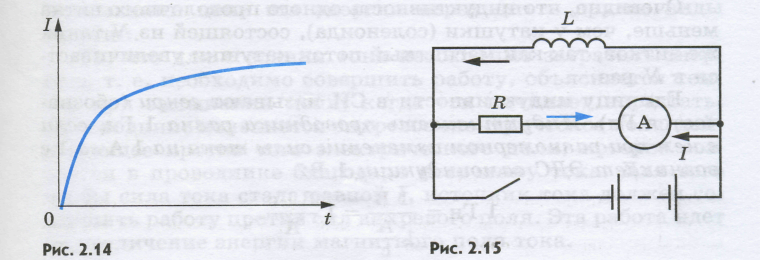ри замыкании ключа первая лампа вспыхивает прак­тически сразу, а вторая — с заметным запозданием. ЭДС са­моиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (рис.).

Появление ЭДС самоиндукции при размыкании:

При размыкании ключа в катушке L возни­кает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальва­нометр идет ток (от R к A), направленный против начального тока до размыкания (I к амперметру). Сила тока при размыкании цепи может превышать силу тока,

проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции ε_IS. больше ЭДС ε ба­тареи элементов.

2. Индуктивность. Модуль вектора индукции магнит­ного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален , то Ф ~ В ~ I. Можно утверждать, что Ф=LI, (1)

где L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком. Величину L называют индуктивностью контура, или его коэффициен­том самоиндукции.

Используя закон электромагнитной индукции и выра­жение (1), получаем равенство

ε_IS = -= -L (2), если считать, что форма контура остается неизменной и по­ток меняется только за счет изменения силы тока. Из формулы (2) следует, что индуктивность — это фи­зическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на 1 А за 1 с.

Индуктивность зависит от геометрических факторов: размеров проводника и его фор­мы, но не зависит непосредственно от силы тока в провод­нике. Кроме геометрии проводника, индуктивность зави­сит от магнитных свойств среды, в которой находится проводник.

Индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивает­ся в N раз.

Единицу индуктивности в СИ называют генри (обозна­чается Гн). Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В: 1 Гн == 1

3. Энергия магнитного поля тока

Согласно закону сохранения энергии энергия магнит­ного поля, созданного током, равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При размыкании цепи ток исчезает, и вихревое поле со­вершает положительную работу. Запасенная током энер­гия выделяется. Это обнаруживается, например, по мощ­ной искре, возникающей при размыкании цепи с большой индуктивностью.

Записать выражение для энер­гии тока I, текущего по цепи с ин­дуктивностью L, (т. е. для энергии магнитного поля тока), можно на основании аналогии между инер­цией и самоиндукцией.

Если самоиндукция аналогична инерции, то индуктивность в про­цессе создания тока должна играть ту же роль, что и масса при увели­чении скорости тела в механике. Роль скорости тела в электродина­мике играет сила тока I как ве­личина, характеризующая движение электрических зарядов.

Если это так, то энергию тока W_м можно считать величиной, подобной кинетической энергии тела в ме­ханике, и записать в виде W_м = (**)

Именно такое выражение для энер­гии тока и получается в резуль­тате расчетов.

Энергия тока (**) выражена через геометрическую характеристи­ку проводника L, и силу тока в нем I. Но эту же энергию можно выра­зить и через характеристики поля. Вычисления показывают, что плотность энергии магнитного поля (т. е. энергия единицы объема) пропор­циональна квадрату магнитной ин­дукции w_М ~ В², подобно тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля w_Э ~ Е²

Запомни: Магнитное поле, созданное элек­трическим током, обладает энергией, прямо пропорциональной квадрату силы тока.

Основные формулы:

Закон Фарадея (законом электромагнитной индукции): ε = – ,где ΔФ — изменение магнитного потока, Δt — промежуток време­ни, за которое это изменение произошло.

Явление самоиндукции заключается в том, что при изменении тока в цепи возникает ЭДС, противодействующая этому изменению. Магнитный поток Ф через поверхность, ограниченную контуром, прямо пропорционален силе тока I в контуре: Ф = LI,

где L — коэф­фициент пропорциональности, называемый индуктивностью.

ЭДС самоиндукции выражается через изменение силы тока в цепи ΔI следующей фор­мулой:

ε = - = -L где Δt — время, за которое это изменение произошло.

Энергия магнитного поля W выражается формулой: W=

Задачи. Самоиндукция. Индуктивность.

1. Какая ЭДС самоиндукции возникает в катушке с индуктивностью 86 мГн, если ток 3,8А исчезает в ней за 0,012 с?

2. Определить ЭДС самоиндукции, если в катушке с индуктивностью 0,016 мГн сила тока уменьшается со скоростью 0,5 к А /с.

3. Какова индуктивность катушки, если при равномерном изменении в ней тока от 2 до 12 А за 0,1 с возникает ЭДС самоиндукции, равная 10 В?

4. Магнитный поток, пронизывающий контур проводника сопротивлением 0,2 Ом, равномерно изменяется с 1,2∙10^-3 Вб до 0,4∙10^-3 Вб за 2 мс. Определить силу тока в контуре.

5. В катушку сопротивлением 2 Ом течёт ток 3 А. Индуктивность катушки 50 мГн. Каким будет напряжение на зажимах катушки, если ток в ней равномерно возрастает со скоростью 200 А/с?

6. Какова скорость изменения силы тока в обмотке реле с индуктивностью 3,5 Гн, если в ней возбуждается ЭДС самоиндукции 105 В?

7. Катушку с ничтожно малым сопротивлением и индуктивностью 3 Гн присоединяют к источнику тока с ЭДС 15 В и ничтожно малым внутренним сопротивлением. Через какой промежуток времени сила тока в катушке достигнет 50А?

8. Катушка индуктивностью 0,2 Гн подключена к источнику тока с ЭДС =10 В и внутренним сопротивление 0,4 Ом. Определить общую ЭДС в момент размыкания цепи, если ток в ней исчезает за 0,04 с, а сопротивление проволоки катушки 1,6 Ом.

9. Катушка сопротивлением 10 Ом и индуктивностью 0,01 Гн находится в переменном магнитном поле. Когда создаваемый этим полем магнитный поток увеличился на 0,01 Вб, ток в катушке возрос на 0,5 А. Какой заряд прошёл за это время по катушке?

http://landing.megapost.info/phisic/

8