Статика твердого тела

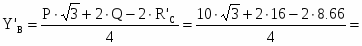
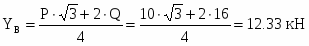
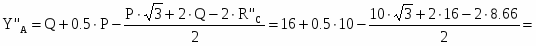
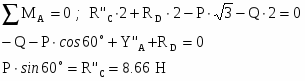
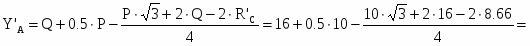
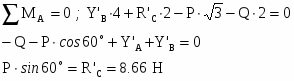
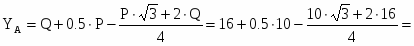
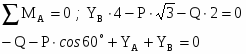
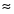
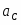
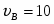
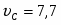
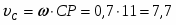
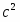
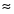
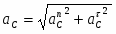
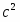
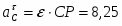
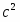
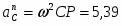
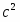
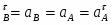
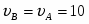
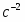
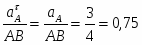
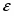
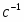
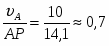
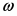
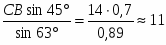
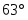
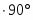
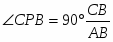
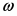
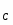
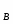
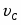
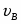
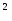
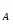
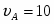
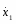
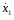
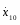
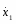
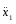
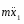
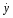
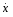
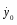
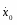
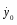
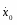
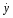
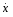
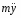
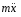
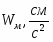
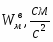
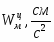
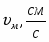
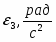
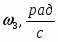
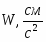
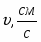
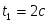
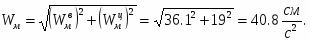
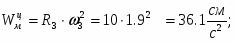
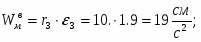
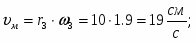
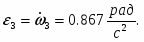
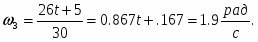
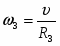
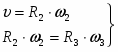
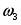
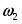
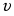
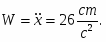
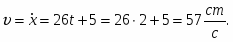
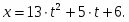
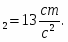
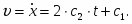
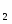
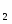
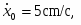
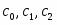
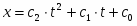
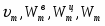
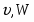
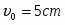
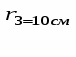
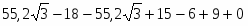
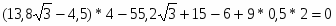
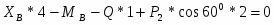
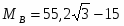
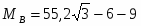
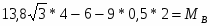
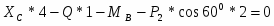
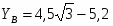
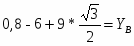
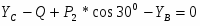
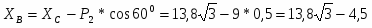
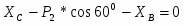
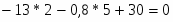
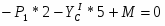
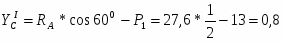
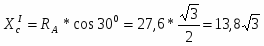
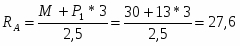
Задание С3

Дано:

P₁=13,0 kH

M=30,0 kH*M ;

M_B - ?

Решение:

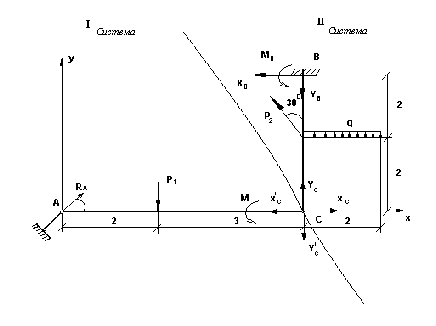
I система

P₂=9,0 kH Σ_x=0;

R_A*cos30^o – X^I_C=0;

q=3,0 kH/M Σ_y=0;

R_A*cos60^o – P₁ – Y^I_C=0

ΣM_C=0;

M+P₁*3-2,5*R_A=0;

;

Проверка

ΣM_A=0;

;

-26 - 4+30=0;

0=0; верно.

II система

Σ_x=0;

;

Σ_y=0;

;

ΣM_B=0;

;

Проверка

ΣM_C=0;

;

0=0; верно.

Дано:

R=20cм; r=10cм; R=30cм;x=6cм;x=356cм; t=2c; t=5c.

Определить

Уравнение движения груза;
-?
-?

Решение:

1) Уравнение движения груза 1 имеет вид:

(1)

Коэффициенты могут быть определены из следующих условий:

при t=0 x=6cм, (2)

при t=2c x=356cм. (3)

Скорость груза 1:

(4)

Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты

с=6см, с=5, с

Таким образом, уравнение движения груза

2) Скорость груза 1

(6)

Ускорение груза 1

3) Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза и угловые скорости колёс и .

В соответствии со схемой механизма:

откуда

или с учетом (6) после подстановки данных:

Угловое ускорение колеса 3:

Скорость точки М, её вращательное, центростремительное и полное ускорения определяются по формулам:

Результаты вычислений для заданного момента времени приведены в табл. 1.

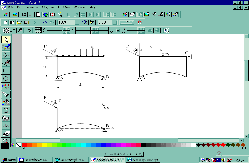
Скорости и ускорения тела 1 и точки М показаны на рис. 1.

Таблица 1

1.9

0.867

36.1

40.80

В 20. Д – 1

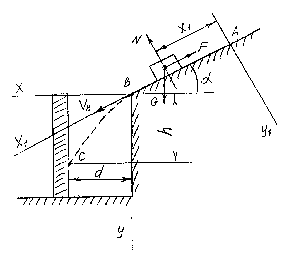
Дано: V_A = 0,  = 45, f = 0,3, d = 2 м, h = 4 м.

Найти: ℓ и .

Решение: Рассмотрим движение камня на участке ВС. На него действует только сила тяжести G. Составляем дифференциальные уравнения движения в проекции на оси X , Y: = 0 , = G ,

Дважды интегрируем уравнения: = С₁, = gt + C₂ ,

x = C₁t + C₃ , y = gt²/2 + C₂t + C₄ ,

Для определения С₁, C₂ , C₃, C₄ , используем начальные условия (при t = 0): x₀ = 0 , y₀ = 0 , = V_Bcos, = V_Bsin ,

Отсюда находим:

= С₁ ,  C₁ = V_Bcos, = C₂,  C₂= V_Bsin

x₀ = C₃ ,  C₃ = 0 , y₀ = C₄ ,  C₄ = 0

Получаем уравнения:

= V_Bcos , = gt + V_Bsin

x = V_Bcost, y = gt²/2 + V_Bsint

Исключаем параметр t :

y = gx² + xtg ,

2V²_Bcos²

В точке С x = d = 2 м , у = h = 4 м. Подставляя в уравнение d и h , находим V_B :

V²_B = gx² = 9,814 = 19,62 ,  V_B = 4,429 м/с

2cos²(y - xtg) 2cos²45(4 - 2tg45)

Рассмотрим движение камня на участке АВ. На него действуют силы тяжести G, нормальная реакция N и сила трения F. Составляем дифференциальное уравнение движения в проекции на ось X₁:

= Gsin - F , (F = fN = fGcos)  = gsin - fgcos,

Дважды интегрируя уравнение, получаем:

= g(sin - fcos)t + C₅ , x₁ = g(sin - fcos)t²/2 + C₅t + C₆ ,

По начальным условиям (при t = 0 x₁₀ = 0 и = V_A = 0) находим С₅ и С₆:

C₅ = 0 , C₆ = 0,

Для определения ℓ и  используем условия: в т.B (при t = ) , x₁ = ℓ , = V_B = 4,429 м/с. Решая систему уравнений находим:

= g(sin - fcos)t  4,429 = 9,81(sin45 - 0,3cos45) ,   = 0,912 с

x₁ = g(sin - fcos)t²/2 ℓ = 9,81(sin45 - 0,3cos45)0,912²/2 = 2,02 м .

Дано:

АВ=20 см.

АС=6 см.

см/с

a=15 cм/c

Найти: , , a, a, ,

Решение:

ОА=ОВ=14,1 см.

=0,7=

СP=см.

см/с

a=15 см/,

т.к. ползуны двигаются по направляющим и совершают только поступательное движение.

см/

9,85 см/

см/с

Ответ:

см/с

9,85 см/

=15 см/

Статика твердого тела

I. Плоская система сил система произвольно расположенных сил

Определение реакций опор твердого тела

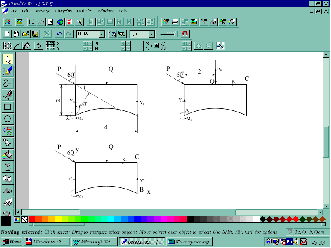
На схеме показаны три способа закрепления бруса. Задаваемая нагрузка и размеры (м) во всех трех случаях одинаковы.

Р = 10 кН, q = 4 кН/м, исследуемая реакция Y_A

Определить реакции опор для того способа закрепления бруса, при котором исследуемая реакция Ya имеет наименьший модуль.

Дано: схемы закрепления бруса ( а, б, в): Р = 10 кН; q = 4 кН/м.

Определить реакции опор для того способа закрепления, при котором реакция Y_A имеет наименьшее числовое значение.

Решение

Рассмотрим систему уравновешивающихся сил, приложенных к конструкции. Действие связей на конструкцию заменяем их реакциями (рис. 2): в схеме а — X_А, Y_А, Y_В в схеме б — Y’_А, Y’_В и R_C, в схеме в — Y”_А, R_C, R_D. Равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей