Статистика кинематика и динамика
Задание 1 СТАТИКА. Для одного из заданных положений плоского механизма составить уравнения и определить величину и направление технологической силы Qm, удерживающую механизм в равновесии при действии на звенья сил тяжестей и уравновешивающего момента Mур =0,8 Нм, приложенного к ведущему звену AB.
Задание 2 КИНЕМАТИКА. Для заданных положений ведущего звена построить планы скоростей и ускорений (при w1=50 ед/с), и определить величину и направление линейных скорости и ускорения т.С.
Задание 3 ДИНАМИКА. Для одного из заданных положений механизма ABCD, при действии на ведущее звено AB внешнего момента Мдв = 0,8 Н∙м и технологической силы Qт, действующей на звено CD в точке К, методом КИНЕТОСТАТИКИ определить значения реакций в опорах (точки А и D), приняв ω1 = 50 рад/сек. Написать уравнение для определения кинетической энергии системы. Значения сил тяжести принять равным: Р1 = 0,5 Н, Р2 = 1,5 Н, Р3 = 0,7 Н. Длины звеньев механизма измерить на рисунке.
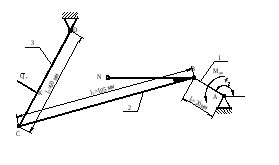
Рисунок . Исходные данные.
Задание 1. СТАТИКА
Напишем условия равновесия для положения механической системы с учетом сил тяжестей звеньев, уравновешивающего момента Mур равного движущему моменту Mдв, показанной на рисунке 2. Данная схема представляет собой систему тел. Для решения данной задачи необходимо расчленить систему на стержни, а действие утраченных связей заменить реакциями (внутренними силами).
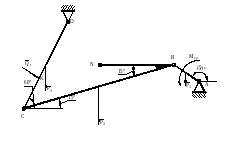
Рисунок . Схема с указанием сил тяжести.
Изобразим силы тяжести звеньев, силы реакции опор.
Равновесие звена DC

Рисунок . Равновесие звена DC.
Запишем уравнения статики для звена DC. Для этого выберем положение начала координат для данного звена в точке D.
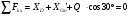 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)
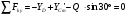 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)
Равновесие звена NBC
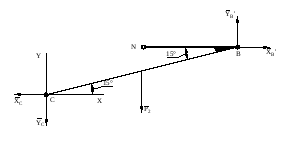
Рисунок . Равновесие звена NBC
Запишем уравнения статики для звена NBC. Для этого выберем положение начала координат для данного звена в точке C.
Равновесие звена AB

Рисунок . Равновесие звена AB.
Запишем уравнения статики для звена NBC. Для этого выберем положение начала координат для данного звена в точке А.
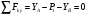 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)
Для нахождения технологической силы 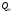 воспользуемся уравнением :
воспользуемся уравнением :
Так как 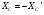 , а также
, а также 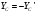 , то выражение принимает вид:
, то выражение принимает вид:
 .
.
Таким образом, осталось определить значения 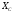 и
и 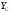 . Значения этих реакций связи определим из уравнений , , :
. Значения этих реакций связи определим из уравнений , , :
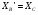
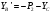
Так как  , а также
, а также 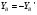 , то:
, то:
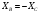
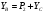
Формула принимает следующий вид:
 .
.
Теперь необходимо совместно решить систему уравнений, состоящую из уравнений и .
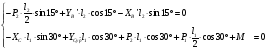
Перепишем каждое уравнение относительно 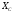 и
и 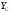 :
:

Подставим значения длин звеньев, сил тяжести и уравновешивающего момента.
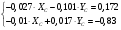
В результате решения данной системы получаем следующие значения:
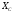 = 55,1 Н;
= 55,1 Н;
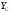 = -16,4 Н.
= -16,4 Н.
При подстановке полученных значений реакций связи в уравнение , получим значение технологической силы:
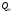 = 58,9 Н.
= 58,9 Н.
Задание 2. КИНЕМАТИКА
Построение плана скоростей. Определяем виды относительного движения звеньев: звенья 1 и 3 совершают вращательное движение, а звено 2 – плоско-параллельное.
Линейную скорость точки B звена 1 определяем по формуле :
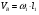 ,
,
где 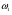 – угловая скорость звена 1, с-1.
– угловая скорость звена 1, с-1.
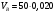 = 1 м/с.
= 1 м/с.
Необходимо построить планы скоростей и ускорений для трёх положений звеньев механизма. Первое из положений показано на рисунке 1, при котором угол φ1 = 150º.
На плане скоростей при φ1 = 150º (рисунок 6) скорость VB изображается отрезком pVb. Зададимся величиной этого отрезка 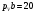 мм и определим масштабный коэффициент плана скоростей:
мм и определим масштабный коэффициент плана скоростей:
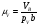
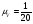 = 0,05
= 0,05  .
.
Скорость точки C определяется из векторной системы уравнений:
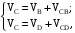
где 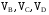 - векторы абсолютных скоростей точек;
- векторы абсолютных скоростей точек;  - векторы относительных скоростей (скорость точки С вокруг B и скорость точки С вокруг опоры D).
- векторы относительных скоростей (скорость точки С вокруг B и скорость точки С вокруг опоры D).
Система уравнений решается графическим способом. При этом учитывается, что 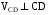 ,
, 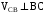 . Скорость точки D равна нулю
. Скорость точки D равна нулю 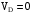 (на плане скорость совпала с полюсом pV).
(на плане скорость совпала с полюсом pV).
Выполним построения для нахождения точки C:
1) Построим скорость 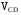 , т.е. скорость точки С вокруг точки D – проведем на плане направление вектора
, т.е. скорость точки С вокруг точки D – проведем на плане направление вектора 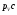 . Из полюса pV проведем линию перпендикулярно звену CD.
. Из полюса pV проведем линию перпендикулярно звену CD.
2) Построим скорость 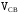 , т.е. скорость точки С вокруг точки B – проведем на плане направление вектора
, т.е. скорость точки С вокруг точки B – проведем на плане направление вектора  через точку b плана скоростей.
через точку b плана скоростей.
3) Точка плана скоростей лежит на пересечении двух направлений 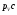 и
и 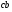 . Достраиваем вектор
. Достраиваем вектор 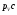 - скорость точки С.
- скорость точки С.
4) Находим величину скорости точки С из плана скоростей:
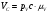
где 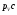 - длина вектора на плане скоростей, мм.
- длина вектора на плане скоростей, мм.
Для плана механизма с φ1 = 150º:
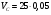 = 1,25 м/с.
= 1,25 м/с.
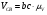
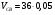 = 1,8 м/с.
= 1,8 м/с.
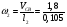 = 17 с-1.
= 17 с-1.
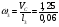 = 21 с-1.
= 21 с-1.
Для плана механизма с φ1 = 180º:
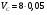 = 0,4 м/с.
= 0,4 м/с.
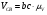
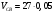 = 1,35 м/с.
= 1,35 м/с.
 = 13 с-1.
= 13 с-1.
 = 7 с-1.
= 7 с-1.
Для плана механизма с φ1 = 210º:
 = 0,5 м/с.
= 0,5 м/с.
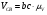
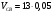 = 0,65 м/с.
= 0,65 м/с.
 = 6 с-1.
= 6 с-1.
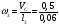 = 8 с-1.
= 8 с-1.
Построение плана ускорений. Ускорение точки B звена 1, совершающего вращательное движение, определяем по формуле

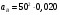 = 50 м/с2.
= 50 м/с2.
Выбираем на плоскости точку pa – полюс плана ускорений. Задаемся величиной отрезка pab = 50 мм, изображающего на плане ускорений нормальную составляющую, и определим масштаб плана ускорений
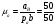 = 1
= 1  .
.
Ускорение точки C определяется из векторных уравнений:
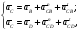
где 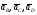 – векторы абсолютных ускорений точек, причем
– векторы абсолютных ускорений точек, причем  ;
;
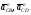 – векторы нормальных ускорений;
– векторы нормальных ускорений;
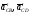 – векторы тангенциальных ускорений.
– векторы тангенциальных ускорений.
Построение плана ускорений для плана механизма с φ1 = 150º (рисунок 6):
Определим значения и длины отрезков нормальных ускорений:

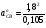 = 31 м/с2.
= 31 м/с2.
в масштабе плана ускорений:

 = 31 мм.
= 31 мм.
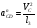
 = 26 м/с2.
= 26 м/с2.
в масштабе плана ускорений:
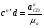
 = 26 мм.
= 26 мм.
Построение плана ускорений для плана механизма с φ1 = 180º (рисунок 7):
Определим значения и длины отрезков нормальных ускорений:

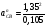 = 17 м/с2.
= 17 м/с2.
в масштабе плана ускорений:

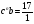 = 17 мм.
= 17 мм.
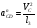
 = 3 м/с2.
= 3 м/с2.
в масштабе плана ускорений:
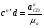
 = 3 мм.
= 3 мм.
Построение плана ускорений для плана механизма с φ1 = 210º (рисунок 8):
Определим значения и длины отрезков нормальных ускорений:

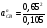 = 4 м/с2.
= 4 м/с2.
в масштабе плана ускорений:

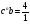 = 4 мм.
= 4 мм.
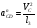
 = 4 м/с2.
= 4 м/с2.
в масштабе плана ускорений:
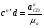
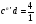 = 4 мм.
= 4 мм.
Угловые ускорения звеньев 2 и 3 определяем по формулам:
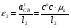 ;
;
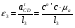
Угловые ускорения для плана механизма с φ1 = 150º:
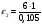 = 57 с-2;
= 57 с-2;
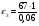 = 1117 c-2.
= 1117 c-2.
Угловые ускорения для плана механизма с φ1 = 180º:
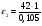 = 400 с-2;
= 400 с-2;
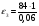 = 1400 c-2.
= 1400 c-2.
Угловые ускорения для плана механизма с φ1 = 210º:
 = 457 с-2;
= 457 с-2;
 = 933 c-2.
= 933 c-2.
Выполним построения для нахождения точки C (рисунки 6, 7, 8):
1) Для этого из точки b плана ускорений откладываем параллельно звену BC отрезок 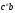 (нормальное направление ускорения) по направлению в сторону движения от точки С к точке В. Перпендикулярно BC проводим через конец этого отрезка линию - тангенциальное направление ускорения.
(нормальное направление ускорения) по направлению в сторону движения от точки С к точке В. Перпендикулярно BC проводим через конец этого отрезка линию - тангенциальное направление ускорения.
2) Из полюса pa плана ускорений откладываем параллельно звену CD отрезок 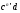 (нормальное направление ускорения) по направлению в сторону движения от точки С к точке D. Перпендикулярно CD проводим через конец этого отрезка линию - тангенциальное направление ускорения.
(нормальное направление ускорения) по направлению в сторону движения от точки С к точке D. Перпендикулярно CD проводим через конец этого отрезка линию - тангенциальное направление ускорения.
3) Пересечением 2-линий тангенциальных направлений получится точка C – вектор  .
.
4) Находим величину ускорения точки С из плана ускорений:
Для плана механизма с φ1 = 150º:
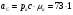 = 73 м/с2;
= 73 м/с2;
Для плана механизма с φ1 = 180º:
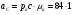 = 84 м/с2;
= 84 м/с2;
Для плана механизма с φ1 = 210º:
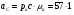 = 57 м/с2;
= 57 м/с2;
ε3 ω1 ε2 ω2 ω3
Рисунок . План механизма (а), скоростей (б) и ускорений (в) при φ1 = 150º.
ε3 ω3 ε3 ε2 ω2 ω1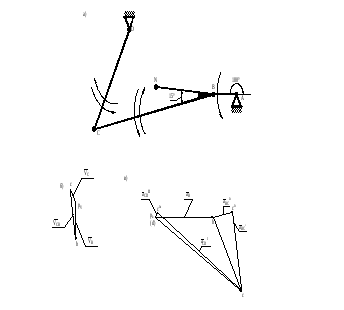
Рисунок . План механизма (а), скоростей (б) и ускорений (в) при φ1 = 180º.
ω1 ω2 ε2 ω3 ε3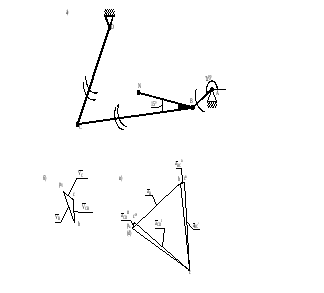
Рисунок . План механизма (а), скоростей (б) и ускорений (в) при φ1 = 210º.
Построение траекторию движения точки N. Для этого построим планы механизма для 12-ти положений: φ1 = 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360.

Рисунок . Построение планов механизма для 12-ти положений.
Построение планов механизма будем производить методом засечек:
Определим траекторию движения точки B путём построения с помощью циркуля окружности с центром A радиусом, равным l1;
Далее с помощью циркуля построим дугу траектории движения точки C. Затем для каждого положения точки B с помощью циркуля проведём засечки на дуге, определяющей траекторию движения точки C, радиусом l2. На пересечении засечек с дугой, определяющей траекторию движения точки C, будут определены положения точки C;
Далее для каждого положения точки B с помощью циркуля проводим дугу радиусом 50 мм, проводим прямую через точку B, составляющую со звеном CB угол 15º. На пересечении полученной дуги с прямой получим точку N;
Далее соединим все полученные положения точки N таким образом получив траекторию движения точки N.
Задание 3. ДИНАМИКА
Значения реакций в опорах определим для положения механизма φ1 = 150º, изображённого на рисунке 10
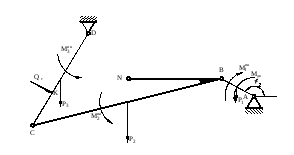
Рисунок . Положение механизма при φ1 = 150º
Изобразим активные силы и силы инерции, действующие на систему (рисунок 10).
Чтобы найти реакции звеньев 1 и 3 последовательно рассмотрим "равновесие" двух кинематических групп.
Расчёт звеньев 2-3.
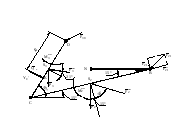
Рисунок . "Равновесие" кинематической группы 2-3.
Вначале рассмотрим звено 2:
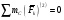
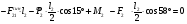 .
.
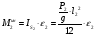
 0,008 Н∙м.
0,008 Н∙м.
Направлен момент инерции в сторону, противоположную угловому ускорению.
Определим из уравнения статики 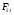 :
:


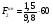 = 9,2 Н.
= 9,2 Н.
Направлена сила инерции в сторону, противоположную ускорению центра масс системы.
 = 1,8 Н.
= 1,8 Н.
Согласно измерениям на рисунке 6 и значению  :
:
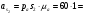 60 м/с2.
60 м/с2.
Рассмотрим сумму моментов для группы звеньев 2-3 относительно точки D:
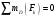
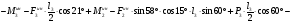
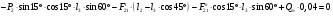
Определим из уравнения статики 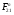 :
:
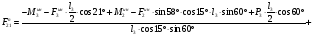
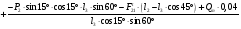
 = 0,03 Н∙м.
= 0,03 Н∙м.
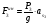
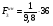 = 3,7 Н.
= 3,7 Н.
Согласно измерениям на рисунке 6 и значению  :
:
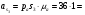 36 м/с2.
36 м/с2.
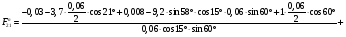
 = 40,6 Н.
= 40,6 Н.
Полная реакция в паре B равна:
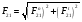
 = 40,6 Н.
= 40,6 Н.
Векторное уравнение сил для группы 2-3 позволяет графически определить вектор 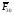 по величине и направлению (рисунок 12).
по величине и направлению (рисунок 12).

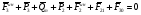
Строим план сил в масштабе
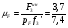 = 0,5 Н/мм.
= 0,5 Н/мм.
Найдем величины отрезков, изображающих на плане сил векторы сил:
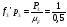 = 2 мм;
= 2 мм;
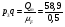 = 118 мм;
= 118 мм;
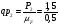 = 3 мм;
= 3 мм;
 = 18 мм;
= 18 мм;
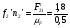 = 4 мм;
= 4 мм;
 = 81 мм;
= 81 мм;
Из плана сил определяем
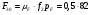 = 41 Н.
= 41 Н.
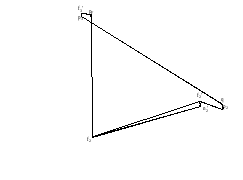
Рисунок . План сил для определения 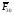 .
.
Расчёт начального звена 1.

Рисунок . "Равновесие" начального звена 1
Из векторного уравнения сил для звена 1 графически определяем вектор 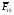 по величине и направлению:
по величине и направлению:
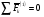
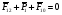
Строим план сил (рисунок 14) в масштабе
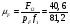 = 0,5 Н/мм.
= 0,5 Н/мм.
Найдем величину отрезка, изображающего на плане сил вектор силы 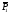 :
:
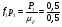 = 1 мм;
= 1 мм;
Из плана сил определяем
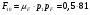 = 40,5 Н.
= 40,5 Н.

Рисунок . План сил для определения 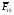 .
.
Напишем уравнение для определения кинетической энергии системы:
 .
.
Для определения кинетической энергии системы определим кинетическую энергию каждого из тел, входящих в систему.
Кривошип 1 совершает вращательное движение относительно неподвижной оси, поэтому его кинетическая энергия равна:
 ,
,
где  – момент инерции кривошипа 1 относительно точки A, кг∙м2.
– момент инерции кривошипа 1 относительно точки A, кг∙м2.
Рычаг 2 совершает плоскопараллельное движение, поэтому его кинетическая энергия равна:
 ,
,
где 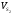 - скорость центра масс рычага 2, м/с;
- скорость центра масс рычага 2, м/с;
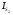 - момент инерции рычага 2 относительно центра масс, кг∙м2.
- момент инерции рычага 2 относительно центра масс, кг∙м2.

Кривошип 3 совершает вращательное движение относительно неподвижной оси, поэтому его кинетическая энергия равна:
 ,
,
где  – момент инерции кривошипа 3 относительно центра масс, кг∙м2.
– момент инерции кривошипа 3 относительно центра масс, кг∙м2.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ \* MERGEFORMAT (.)
\* MERGEFORMAT (.) \* MERGEFORMAT (.)
\* MERGEFORMAT (.) \* MERGEFORMAT (.)
\* MERGEFORMAT (.)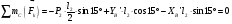 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)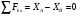 \* MERGEFORMAT (.)
\* MERGEFORMAT (.) \* MERGEFORMAT (.)
\* MERGEFORMAT (.)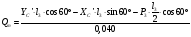 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)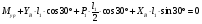 \* MERGEFORMAT (.)
\* MERGEFORMAT (.)