Қазақстан Республикасының білім және ғылым министрлігі

Министерство образования и науки Республики Казахстан

РИИ индустриалды-технологиялық колледжі

Индустриально-технологический колледж РИИ

КОНТРОЛЬНАЯ РАБОТА №1,2

по дисциплине: «Основы технической механики»

по разделам: «Теоретическая механика. Сопротивление материалов»

Выполнил: Шпис И.

Группа ЗЭ-10 2

Шифр 100480

Преподаватель: Семёнова О.Л.

Рудный 2010

Задача №1 Статика

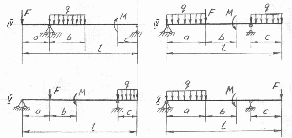
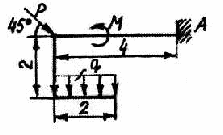
На схеме показаны способы закрепления бруса, ось которого - ломаная линия. Задаваемая нагрузка и размеры указаны в таблице 1.

Требуется определить реакции опор.

Таблица 1 - Исходные данные

Р, кН

М, кН·м

q, кН/м

5

10

2

Решение.

Рассмотрим систему уравновешивающихся сил, приложенных к конструкции. Действие связей на конструкцию заменяем их реакциями Х_А, Y_А, М_А. Равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей:

Q = q·2 = 2 ·2 = 4 кН

Р_х = Р·cos45⁰=5·0,707=3,53 кН

P_y=P·sin45⁰=5·0,707=3,53 кН

Момент в заделке найдем, не определяя пока остальных реакций

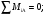М_А - Р·2 sin 45° + М - Q·5 = 0.

Вычисления дают:

М_А= 17,07 кН·м.

Определим остальные опорные реакции для этой схемы:

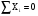Х_А+Р_Х=0 Х_А= -Р_Х= -3,53 кН

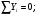Y_A-P_Y-Q=0 Y_A= P_Y+ Q=3,53+4=7,53кН

Проверка:

ΣМ_В=0

-Y_A·2+M_A+M-Q·3=0

-7,53·2+17,07+10-12=0

12.01-12=0

-0,01=0

ε=0.01/12.01·100%=0,008% (допускается погрешность до 0,1%)

Задача№2 Растяжение

На короткий чугунный брус круглого поперечного сечения действуют растягивающие и сжимающие усилия. Требуется спроектировать брус равного сопротивления, для чего:

1) разбить брус на участки (пронумеровав их, начиная от свободного конца) и на каждом участке найти внутреннюю продольную силу;

2) построить эпюру внутренних продольных сил;

3) из расчета на прочность определить для каждого участка бруса необходимый диаметр поперечного сечения и подобрать (для каждого участка) окончательную величину диаметра в соответствии с таблицей нормальных размеров;

4) начертить схему бруса с учетом найденных размеров сечений. Для спроектированного бруса:

5) найти на каждом участке напряжения и построить эпюру напряжений

F

кН

[σ_Р]

МПа

[σ с]

МПа

а

м

55

55

120

0.18

1. Построение эпюры N

Решение задачи начинается от свободного конца бруса. Это позволяет начать построение эпюры N без определения реакции опоры. Эпюра N строится методом сечений. Разделяем брус на участки. Границами участков являются точки приложения внешних сил, перемена сечения бруса и опора.

Границы участков обозначим буквами а, b, с, d, e.

I участок (ab)

N₁=-2F= -110 кН (сжатие)

II участок (bс)

N₂=-2F-4F=-6F=-330 кН (сжатие)

III участок (cd)

N₃==-2F-4F+13F=7 F=385кН (растяжение)

IV участок (de)

N₄=2F-4F+13F+5F=12F=660 кН (растяжение)

2. Строим эпюру N начиная от свободного конца бруса. Сначала проводим нулевую горизонтальную линию, далее откладываем значения подсчитанной продольной силы (положительные значения вверх, отрицательные вниз).

3. Определяем диаметр каждого участка

Условие прочности при растяжении:

,

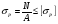Условие прочности при сжатии:

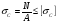
где А – площадь поперечного сечения бруса

Для бруса круглого поперечного сечения:

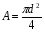
где d- диаметр бруса.

Подставляя в условие прочности и выражая значение диаметра получаем:

Для растяжения:

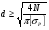
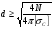
Для участков:

I участок (ab):

d₁ = √ 4·110/(3.14·12) = 11.67

По таблице нормальных размеров принимаем d₁=12 мм

II участок (bс):

d₂ = √ 4·330/(3.14·12) = 35.03

Принимаем d₂=36 мм

III участок (cd):

d₃ = √ 4·385/(3.14·5.5) = 89.17

Принимаем d₃=90 мм.

IV участок (de)

d₃ = √ 4·660/(3.14·5.5) = 152.8

Принимаем d₄=153 мм.

4 Строим схему бруса с учетом найденных значений диаметров

Посторенние начинаем с проведения штрихпунктирной линии, изображающей центр бруса, затем по участкам откладываем значения диаметров.

5 Находим на каждом участке напряжения и строим эпюру напряжений

Значение нормальных напряжений на участке определяем по формуле:

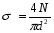
I участок (ab)

σ₁ = 4·(-110)/3.14·(1.2)² = -97.7

II участок (be)

σ₂ = 4·(-330)/3.14·(3.6)² = -32.44

III участок (cd)

σ₃ = 4·(385)/3.14·(9)² = 6.05

IV участок (de)

σ₄ = 4·(660)/3.14·(15.3)² = 3.59

Строим эпюру нормальных напряжений, руководствуясь правилами построения эпюры продольных сил.

5F 13F 4F 2F

e d c b a

а а 2а а

660

385

+

+

-

- 110

330

d₄ =153 d₃ =90

d₁ =12

d₂ =36

3.59

+ 6.05

+

-

-

32.44

97.7

Задача №3 Кручение

К стальному ступенчатому валу, имеющему сплошное поперечное сечение, приложены четыре момента. Левый конец вала жестко закреплён в опоре, а правый конец – свободен и его торец имеет угловые перемещения относительно левого конца.

Требуется:

- построить эпюру крутящих моментов по длине вала;

- при заданном значении допускаемого напряжения на кручение определить диаметры d₁ и d₂ вала из расчёта на прочность, полученные значения округлить.

Исходные данные

Расстояние, м

Моменты, кН·м

[τ],

МПа

а

b

с

Т₁

Т₂

Т₃

Т₄

1.3

1.7

1.9

5.8

2.8

1.8

0.8

45

Решение:

1. Построение эпюры М_кр (крутящего момента)

М_крI = -Т₄= -0.8 кН·м

М_крII = -Т₄+Т₃= -0.8+1.8=1кН·м

М_крIII = -Т₄+Т₃+Т₂= -0.8+1.8+2.8=3.8кН·м

М_крΙV = -Т₄+Т₃+Т₂+Т₁= -0.8+1.8+2.8+5.8=9.6 кН·м

По этим данным строим эпюру М_кр

2. Определение диаметров вала

Общее условие прочности при кручении:

τ_кр =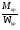

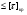
Максимальный крутящий момент для диаметра d₁:

М_кр=9600 Н·м

Максимальный крутящий момент для диаметра d₂:

М_кр=1000Н·м

Момент сопротивления при кручении:

W_кр =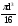

Подставляем значение в общее условие прочности:

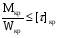
Получаем значение диаметра:

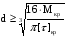
Вычисляем значение диаметров:

d₁=³√ 16·8200/3.14·45·10⁶ ≥ 0.17

d₂=³√ 16·1000/3.14·45·10⁶ ≥ 0.05

Принимаем d₁=115мм, d₂=50мм по таблице нормальных размеров.

ΙV Т₁ Т₂

ΙΙΙ

ΙΙ Т₃ Ι

d₁ d₂

Т₄

а b c a

9.6

3.8

+

+ 1

+

0.8

-

Задача №4 Изгиб

Для заданной схемы балки требуется написать выражение для определения изгибающего момента для каждого участка в общем виде, построить эпюру М, найти М_мах и подобрать стальную балку двутаврового поперечного сечения при [σ]= 160 МПа.

Таблица 5 – Исходные данные

а, м

b, м

с, м

l, м

М,

кН·м

F,

кН

q,

кН/м

2.6

4.6

2.7

11

10

10

15

Уравнение прочности при изгибе в общем виде:

σ _и =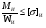

1.Составляем расчётную схему и методами теоретической механики определяем реакции в опорах. Предварительно определяем размер d:

d=l-(a+b+c) =11- (2.6+4.6+2.7) =1.1 м

ΣМ_А= 0 , - (2q·а) · (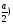 - P·d +R_B · (d+b) +M = 0

R_B=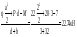

15·3.38+10·1.1-10

R_B=————————— = 29.52

1.1+4.6

ΣМ_B =0

- (2q·а)·(b+d+(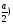)-R_А(d+b)+P·b+М=0

R_А=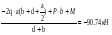

-30·(4.6+1.1+1.3)+10·4.6+10

R_А= ——————————————— = -27.01

1.1.+4.6

т.е. реакция направлена в другую сторону, чем на схеме.

2.Определяем изгибающие моменты, действующие по длине балки, используя правило знаков для изгибающего момента.

Изгибающий момент на участке с координатой Х₁:

М_И1=2q·Х₁·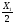

при Х₁=0,М_И=0

при Х₁=а, М_И=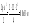 30·6.76/2 = 101.4

(кривая на эпюре парабола, т.к. переменная Х₁ во второй степени).

Изгибающий момент на участке с координатой Х₂:

М_ИII= 2q·а ·(Х₂-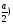+R_A·(Х₂-а)

при Х₂=а, М_И =2q·а· (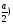+R_А·(а-а)=101.4 кН·м

Это значение совпадает со значением момента в этой опоре на предыдущем участке.

при Х₂= а +d, М_И =2q·а ·(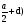+R_A· (а +d-а)=157.5 кН·м

Изгибающий момент на участке с координатой Х₃:

М_ИIII =2q·а·(Х₃-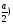-R_А·(Х₃-а)- Р·(Х₃-а-d)

при Х₃=а+d, М_И=214.21 кН·м

Это значение совпадает со значением момента в этой точке балки на предыдущем участке.

при Х₃=а+d+b, Ми=6.53 кН·м

Изгибающий момент на участке с координатой Х₄ равен моменту М, который задан в условии задачи.

М_ИIV=М=7кН·м

На предыдущем участке момент в этой опоре был равен 6.53 кН·м, разница в значениях моментов это погрешность расчёта.

На основании расчётов строим эпюру изгибающих моментов.

3. Определение опасного сечения балки.

Опасным сечением будет являться то сечение, в котором изгибающий момент максимальный. Это сечение в опоре А, изгибающий момент в котором равен 101.4Н·м. Подбираем номер двутавра по формуле:

W_Х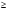

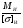
где М_И-максимальный изгибающий момент, кН·м

W_X - момент сопротивления двутавра, см³.

[σ]_И - допускаемое напряжение на изгиб, МПа

[σ]_И=160 МПа=16 кН/см³

W_X ≥ 101000/16000 = 630 см²

Номер двутавра по моменту сопротивления подбирается по таблице.

Значения момента сопротивления для двутавров

№

W_x

№

W_x

10

39.7

27

371

12

58.4

27а

407

14

81.7

30

472

16

109

30а

518

18

143

33

597

18а

159

36

743

20

184

40

953

20а

203

45

1231

22

232

50

1589

24

289

55

2035

24а

317

60

2560

Принимаем двутавр №36 с W_x=743см².

а d b c

e

Х₄

Х₁

Х₂

Х₃

214.21

101.4

7

Список использованной литературы.

1. Сборник заданий для курсовых работ по теоретической механике: Учеб. Пособие для техн. вузов/ Яблонский А.А., Норейко С.С., Вольфсон С.А. и др.; М.: Высш. шк., 1985.

2. Стёпин П.А. Сопротивление материалов: Учебник для немашиностроительных специальностей вузов.-7-е изд.-М.: Высш. шк., 1983.

3. Яблонский А.А, Курс теоретической механики часть 1: Учебник для машиностроительных, механических, приборостроительных, электротехнических и строительных специальностей вузов. М.: Высш. шк, 1963.: ил.