П Л А Н.

Вступ

Розділ 1. Дифракція і принцип Гюйгенса

1.1 Порушення прямолінійного поширення світла

1.2 Когерентність

1.3 Порушення принципу незалежності світлових пучків

1.4 Принцип суперпозиції. Інтерференція

Розділ 2. Дифракція і принцип Гюйгенса-Френеля

2.1 Розташування і ширина максимумів дифракції на екрані

2.2 Умови чіткого спостереження дифракції від однієї щілини

Розділ 3. Дифракційна природа оптичного зображення

3.1 Критерій Релея

3.2 Роздільна здатність мікроскопа і телескопа

3.3 Дифракційна гратка

Висновки

Список використаних джерел

ВСТУП

Розділ оптики про хвильові властивості світла – це частина так званої фізичної оптики. У променевій або геометричній оптиці розглядаються такі питання, які можна розв’язати на основі уявлень про світлові промені та закони відбивання і заломлення світла.

У хвильовій оптиці розглядаються питання, пов’язані з природою світла. Зрозуміти дифракцію, інтерференцію та поляризацію світла можна лише на основі уявлень про його хвильову природу, еволюція яких закінчилась розробкою електромагнітної теорії світла у другій половині XIX століття. Ця теорія стала провідною у вивченні цих та ряду інших явищ, як, наприклад, дисперсія світла.

Виявилось, що всі закони променевої оптики мають обмежений характер і що їх можна теоретично вивести на основі уявлень про хвильову природу світла. Як відомо, оптичні прилади розглядаються в геометричній оптиці, але важливе питання про можливості відрізняти дуже малі деталі об’єкта (роздільна здатність оптичних приладів) можна розв’язати, тільки враховуючи хвильові властивості світла.

Отже, поділ оптики на геометричну і хвильову – умовний, тому променеву оптику не слід вивчати відокремлено від хвильової теорії світла.

Більшу частину курсу оптики учні вивчають на основі умовного поняття про промінь і тільки згодом, в темі про інтерференцію та дифракцію, довідуються про хвильові властивості світла. Але це здається учням дрібним і незначним і істотно на формування їх знань з фізики не впливає. Насправді хвильові і квантові явища, що розглядаються в хвильовій оптиці, мають величезне наукове, освітнє і практичне значення.

Електромагнітна теорія світла належить до найважливіших теорій фізики і має величезне наукове значення. Пов’язуючи електромагнітні і оптичні явища, вона стверджує основні погляди діалектичного матеріалізму про взаємозв’язок між явищами природи.

Розділ 1.

Дифракція і принцип Гюйгенса

1.1. Порушення прямолінійного поширення світла

Вивчення будь-яких фізичних явищ починають із встановлення емпіричних фактів, тобто знань, одержаних дослідним шляхом. Звичайно, що такі емпіричні факти є статистичними узагальненнями спостережень. Спочатку виділимо деякі відомі факти та їх узагальнення, на основі яких можна відтворити найпоширеніші властивості хвильових процесів – інтерференцію і дифракцію світла.

Кожний хвильовий процес (механічні, звуковий, електромагнітний) характеризується періодичністю в просторі й періодичністю в часі. Періодичність у просторі – це коли в даний момент часу на поверхні води можна побачити гребені, а за ними впадини. Якщо ж у даному місці спостерігається спочатку гребінь, а потім впадина – це ознака періодичності в часі. Завдяки періодичності хвильові процеси різної природи описуються подібними математичними рівняннями. Рівняння, що описують світлові явища, зручно інтерпретувати за допомогою механічних хвиль. При цьому потрібно розрізняти графік поширення коливань у середовищі і графік зміни величини (зміщення, напруженості тощо ) від часу в даній точці простору.

Рис.1.

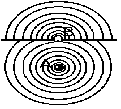
Короткими ударами по поверхні води у хвильовій ванні в деякій точці А можна викликати кільцеві хвилі, що розходяться в усі боки. Ванну перегороджуються екраном з вузькою щілиною В. Коливання, викликані в точці А, проникають крізь щілину В по інший бік екрана. Причому центром збудження цих коливань є не точка А, а щілина В, незалежно від того, в якому місці фронту хвилі вона знаходиться. Досліди з водяною ванною пояснюють відомий принцип Гюйгенса: кожна точка, якої досягає збудження, стає ніби новим центром (джерелом) коливань. Застосовуючи метод аналогії, доходимо висновку, що це характерно для усіх хвиль, у тому числі й світлових.

Факти прямолінійного поширення світла підтверджується повсякденними спостереженнями. Однак ще в 1665 р. італієць Франческо Гримальді звернув увагу на ту обставину, що перехід від світла до тіні відбувається не різко, а з поступовим посиленням освітлення. Він також спостерігав огинання світлом перешкод. Прямолінійність поширення світла порушувалася під час проходження скрізь вузькі щілини і малі отвори. Це явище було названо дифракцією. Для спостереження дифракції від отвору можна вузький промінь ОКГ (оптичного квантового генератора) спрямувати на отвір в непрозорому екрані.

Якщо спостерігати дифракцію від щілин, не важко помітити, що чим вужча щілина тим світло сильніше відхиляється від прямолінійного поширення.

Є дві схеми спостереження дифракції від отвору і щілини, коли, відповідно, світло направляють на отвір і щілину, та коли віддалене джерело світла розглядають крізь отвір і щілину. Отвір і щілина дають не лише дійсне, але й уявне зображення нескінченно віддалених джерел у вигляді дифракційної картини. Оскільки світло - це електромагнітні хвилі, явище огинання світлом перешкод легко пояснити за допомогою відомого принципу Гюйгенса (цей принцип був корисним для пояснення заломлення світла). Однак на основі принципу Гюйгенса можна встановити лише те, що зображення світної точки у формі розмитого світлого диска перевищує розміри отвору (щілини).

1.2. Когерентність

Дифракцію і інтерференцію електромагнітних хвиль можна зафіксувати, якщо хвилі однакової частоти мають сталу різницю фаз і одну площину коливань. Такі узгоджені в просторі і в часі хвилі називаються когерентними. У оптиці мають справу не з довготривалими монохроматичними синусоїдальними хвилями, а із затухаючими коливаннями, так званими цугами хвиль, що являють собою лише відрізки синусоїд (Рис.2). Час висвічування атома (10^-8 с) називають часом когерентності, а довжину цуга –

Атом

Х

Рис. 2

відстанню когерентності ().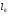

В кожному наступному цугу площина коливань електричного вектора, яка збігається з коливаннями електрона в атомі, щоразу змінюється. Змінюються й фазові співвідношення між окремими випромінюваннями одного і того самого атома. Кожен атом випромінює світло різних частот, яке не є монохроматичним. Тому світлові пучки, що складаються із сукупності багатьох цугів різної частоти, за таких умов некогерентні. Світловий фронт хвиль, створений розжареним тілом, змінюється від точки до точки і від одного моменту часу до іншого. За аналогією він може нагадувати хвильовий фронт, що створюється в калюжі, якщо туди кинути пригорщу камінців. Однак зауважимо, що один камінець (як точкове джерело), кинутий у воду, створює когерентний хвильовий фронт. Продовжуючи подібні порівняння, уявімо собі існування точкових світлових джерел (своєрідних “камінців”), які можуть генерувати когерентні світлові хвилі. Підстава для цього є, бо явища інтерференції й дифракції світла спостерігаються лише при взаємодії когерентних хвиль. Але площина цугів, фази та їх частоти різні, і когерентність світлових пучків не слід розуміти в традиційному смислі. Під когерентністю в оптиці розуміють здатність світлових хвиль до інтерференції. Чим вона зумовлюється?

Відомо, що чим вужча щілина, тим більше світло відхиляється від прямолінійного поширення. Подумки перейдімо до граничного випадку в розвитку цієї закономірності. Якби розміри щілини чи отвору були меншими від довжини хвилі, вона (щілина), напевно, освітлювала б весь екран. Отже, абстрагуючись від ширини щілини (отвору), переходимо до моделі лінійного (точкового) джерела, що випромінює гармонічні хвилі. Однак точкових джерел не існує, як не існує математичних маятників і матеріальних точок. І все-таки це корисна абстракція, оскільки вона дає змогу описувати спонтанне (самодовільне) випромінювання світлових джерел лише однією синусоїдальною хвилею. “Синусоїдальні” коливання від точкових джерел – це випромінювання монохроматичного світла.

Завдяки введенню монохроматичної ідеалізації можна говорити про інтерференцію від двох електромагнітних хвиль. На практиці точковим джерелом можна вважати джерело, розміри якого дорівнюють 250 довжинам хвиль. Розрахунки показують, що джерело світла розміром 0,15 мм мало чим відрізняються від точкового джерела.

Будь-які просторово рознесені точки такого джерела є когерентними. У свій час Юнг замінив вузький отвір великим джерелом світла, і інтерференційна картина на екрані відразу ж зникла. Юнг пояснив це тим, що на щілини потрапляло світло від різних ділянок великого джерела, а таке світло не має властивості просторової когерентності.

Отже, просторова когерентність – це когерентність, яка забезпечується просторовим розміщенням (рознесенням) точкових джерел. Просторова когерентність зумовлюється поділом фронту хвилі.

1.3. Порушення принципу незалежності світлових пучків

Цілком звичним для нас є таке явище. Два світлові пучки, що поширюється від двох електричних ламп, не впливають один на одного. Узагальненням цього явища став відомий із часів Гюйгенса закон незалежності світлових пучків. І лише в 1801р. англійський фізик Томас Юнг здійснив експеримент, що демонстрував інтерференцію світла. Він знайшов такі умови досліду, за які два з’єднанні пучки давали систему темних і світлих смуг, а це означає, “що світло додане, до світла, викликає темряву”. Юнг пропускав сонячне світло скрізь невеликій отвір S в екрані і направляв його на два невеликі близько розміщені отвори S1 і S2 в другому екрані (Рис. 3). Від кожного з них виходили конусоподібні дифрагуючі пучки світла, Що перекривалися один одним. На екрані спостерігається інтервенційна картина. В одному досліді із ОКГ (відстань між точковими діафрагмами становила 0,2 мм, а їх діаметри - 0,05 мм) спостерігається взаємне чергування семи світлих і темних смуг .

Рис. 3

РИСю1

Отже, явища інтерференції й дифракції фіксують, насамперед, порушення прямолінійності поширення світла і незалежності світлових хвиль.

1. 4. Принцип суперпозиції. Інтерференція

Хвилі при одночасному поширенні в певному середовищі взаємно проникні: не відбувається підсилення чи послаблення самих хвиль. Цей факт набув свого відображення у відомому принципі суперпозиції. Суперпозиція – це “здатність фізичних полів до накладання, при якому векторні характеристики додаються геометрично, а після розходження поля існують незалежно одне від одного”. У принципі суперпозиції поєднуються дві, здавалося б, протилежні ознаки хвильових явищ, а саме: незалежність, тобто відсутність взаємодії, вірніше, зв’язку між хвилями, і накладання – наявність зв’язку, взаємодії. Тому виділимо умовно найпоширеніші випадки накладання хвиль.

1. При одночасному поширенні в певному середовищі некогерентні хвилі (хвилі, що відрізняються частотою, площиною коливань і не мають сталої різниці фаз) є незалежними. Саме завдяки суперпозиції ми можемо, наприклад, настроюватися на певну радіостанцію, хоча одночасно радіохвилі випромінюються десятками інших радіостанцій.

2. При накладанні двох когерентних хвиль від двох точкових джерел у точці зустрічі коливання гасяться.

Суперпозиція (накладання) двох когерентних хвиль з утворенням сталої в просторі і часі інтерференційної картини дістала назви інтерференції. При інтерференції хвилі поширюються незалежно одна від одної, а складаються коливання, що надходять у будь-яку точку простору від двох джерел. У момент взаємодії лише в даній точці порушується так званий принцип незалежності світлових пучків. Проте, хоча в точці зустрічі коливання і гасяться, після зустрічі хвилі знову поширюються незалежно одна від одної.

Найпоширенішими випадками інтерференції є:

1. інтерференція від двох точкових джерел (так звана інтерференція за схемою Юнга);

2. інтерференція від протяжних джерел (інтерференція в тонких плівках).

Чи є підстава вважати, що точкові джерела освітлюють екран рівномірно? Звернемося до експерименту, що демонструє інтерференцію світла за схемою Юнга (Рис. 3). Юнг пропускав сонячне світло крізь невеликий отвір в екрані і направляв його на два невеликі близько розміщені отвори в іншому екрані. Від кожного із них виходили дифрагуючі конусоподібні когерентні пучки світла, що перекривали один одного і давали інтерференційну картину. Якщо відтворити цей дослід, то можна переконатись, що ширина максимумів інтерференції і розподіл інтенсивності підтверджується теоретичними розрахунками за умови рівномірного освітлення дисків на екрані, а саме: ширина максимумів інтерференції та їх інтенсивність у центральній частині екрана однакові.

На рис.4 зображена інтерференційна картина від двох нескінченно тонких щілин (одержання її в умовах школи не виявляється можливим). Щілини - це, по суті, сукупність пар проколів (точкових джерел). Картина від щілин більш виразна, ніж від точкових джерел. Відстань 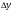між інтерференційними максимумами (мінімумами) дорівнює

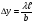, (1)

де b - відстань між щілинами, шириною яких нехтують, 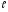- відстань від щілин до екрана, а розподіл інтенсивності світла на екрані

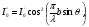(2)

де 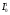- інтенсивність від однієї нескінченно тонкої щілини перпендикулярно до екрана. Тому розподіл інтенсивності світла являє собою серію максимумів однакової висоти.

Однак, насправді при наближенні екрана до отвору дифракційна картина від кожного із отворів освітлена нерівномірно, а конусоподібні пучки світла при їх накладанні дають інтерференційну картину у вигляді сімейства гіпербол (прямі лінії лише в центральній частині). Як пояснити, чому дифракційне зображення окремої світної точки оточене темними кільцями, а в дифракційному зображенні щілини шириною 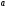(тут ширину враховують) присутні темні вертикальні лінії?

Розділ 2.

Дифракція і принцип Гюйгенса-Френеля.

2.1. Розташування і ширина максимумів дифракції на екрані

Очевидно, утворення світлих і темних смуг пов`язане із відхиленням променів. Припустимо, що світло - потік корпускул. Тоді виникнення світлих і темних ділянок стане можливим, коли взаємодія корпускул із перешкодою залежатиме від відстані між ними стрибкоподібно. Проте гравітаційні сили такої властивості не мають. Отже, результатом розгляду темних смуг повинен бути, насамперед, висновок про хвильову природу світла без посилання на те, що світло - це різновид електромагнітних хвиль, тобто незалежно від теорії Д. К. Максвела.

Більше того, наявність темних смуг дає підставу зауважити, що, мабуть, дифракція - це не просто огинання, це - складне явище. Дослідження дифракційних закономірностей можна провести за кожною з двох вищезгаданих схем спостереження явища, розглянувши такі випадки, коли: а) розміри отвору (щілини) та його відстань до екрана однакова; б) не змінюючи діаметра отвору і його місцезнаходження, наближають і віддаляють від нього екран спостереження; в) змінюють діаметр отвору за постійної відстані від отвору до екрана спостереження. Якщо, до того ж, змінювати відстань від джерела світла до отвору, розрізняють дифракцію Френеля і Фраунгофера. З дифракцією пов`язані різні варіації теоретичних і практичних задач, які не можна пояснити, використовуючи лише принцип Гюйгенса. І тут на допомогу приходить принцип Гюйгенса-Френеля, згідно з яким щілина, якої досягає фронт хвилі, стає джерелом нових вторинних хвиль (на рис.3 їх дванадцять). Хвилі когерентні між собою. Амплітуда і фаза хвилі у будь-якій точці Р- простору - це результат інтерференції хвиль, створених вторинними джерелами (на

Рис. 5

рис. 5 джерела 1 і 7, 2 і 8 тощо).

Оскільки кожна пара осциляторів дає мінімум інтерференції у точці Р, робимо висновок, що в цій точці має місце мінімум дифракції від щілини як множини джерел. Таким чином, при дифракції інтерферують дифраговані пучки світла. Дифракція - відхилення світла від прямолінійного поширення - обумовлена суперпозицією множини когерентних джерел. Користуючись графічною моделлю (рис.2) фізичного явища (дифракція), можна встановити умову першого мінімуму від щілини:

(3)

де 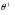- кутова півширина центрального максимуму. Крім того, за її допомогою можна ввести поняття про зони Френеля і розглянути дифракційні закономірності.

Розглянемо теорію дифракції від однієї щілини. Теорія дифракції на одній щілині (отворі) має велике практичне значення при проектуванні мікроскопів і телескопів, вона потрібна для пояснення роздільної здатності дифракційних граток, а також для розуміння дифракційної природи оптичного зображення тощо. Якщо “вилучити” непрозорий проміжок між нескінченно тонкими щілинами, можна отримати щілину певної ширини . Нехай ми маємо своєрідну щілину, що складається з n = 12 джерел, які випромінюють світлові хвилі. Відстань між крайніми джерелами дорівнює , а між сусідніми — ₁, причому  >  (мал.5). Дослідимо зміну картини, що спостерігається на екрані від щілини певної ширини, залежно від просторового кута при незмінному положенні екрана і щілини. Ті промені, для яких  =0, збираються лінзою або інтерферують у нескінченності в точці Р₀ , оскільки сумарна напруженість Е₁ =n E₀ . Виберемо такий напрям поширення променів, при якому різниця ходу між крайнім і середнім променями дорівнює 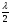. Тоді між крайніми променями ця різниця дорівнює . З мал.5 видно, що від першого осцилятора, який знаходиться у нижній половині щілини, результуюча напруженість дорівнює нулю. Крім того, такі пари осциляторів, як 2 і 8, 3 і 9, 4 і 10, 5 і 11, 6 і 12 в точці Р також створюють результуючу напруженість, що дорівнює нулю (коливання від цих пар осциляторів різняться на 180). З мал. 5 видно, що =₁ n, бо n1. Умову першого мінімуму (“нуля” інтенсивності хвилі) можна записати так:

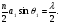(4)

Тому в напрямі, для якого різниця ходу між крайнім і середнім променями дорівнює половині довжини хвилі, тобто 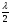, має місце перший мінімум. Умову першого мінімуму перепишемо так:  sin₁ =  .

Отже, якщо різниця ходу між крайніми хвилями дорівнює довжині хвилі, має місце мінімум напруженості в точці Р. Для малих кутів (≤30°)

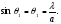(5)

Прийом попарного додавання миттєвих значень напруженості двох світлових хвиль є найпростішим способом встановлення кінцевого результату дифракції від багатьох пар “точкових джерел” щілини.

Слід підкреслити, що кожній точці (зоні) верхньої половини щілини відповідає деяке джерело (зона) з нижньої половини, і їх дії взаємно компенсуються. Отже, умовою першого мінімуму є наявність у щілині парного числа зон, які компенсують одна одну. Ці зони називають зонами Френеля. Зони Френеля – це уявні вузенькі смужки хвильового фронту щілини, різниця відстаней від відповідних (крайніх) точок яких до екрана дорівнює 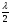. Ширина зони x₁ визначається за умови 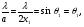тобто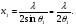

Рис. 6

Виберемо тепер напрям, для якого різниця ходу між середнім і крайнім променями дорівнює , а між крайніми – 2. Отже, різниця ходу між сусідніми хвилями при цьому становить  =60° (Рис.6). У даному разі різниця фаз 180° буде спостерігатися для таких пар осциляторів: 1 і 4, 2 і 5, 3 і 6 (четвертий скомпенсований першим, п’ятий – другим, шостий - третім). Таким чином, маємо чотири зони. Перша, в яку входять джерела 1,2,3, нейтралізується другою (джерела 4,5,6), третя зона, що складається із джерел 7,8,9, компенсується четвертою (джерела 10,11,12).

Для кута ₂ щілину можна уявити як сукупність чотирьох зон Френеля :  =4x₂ . (Тому різниця ходу визначається кількістю зон Френеля: ∆l=4x₂). При цьому ширину знаходять із співвідношення: 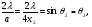або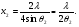

Рис. 7

Для випадку 3=sin₃ відстані між сусідніми джерелами відповідають зсуву фаз на 90° (мал.7). Виділимо ті пари джерел, хвилі від яких відрізняються на 90°: третє джерело компенсується першим, четверте – другим, сьоме – п’ятим, восьме – шостим тощо.

Залишається шість зон, у які входять відповідно джерела 1 і 2, 3 і 4, 5 і 6, 7 і 8, 9 і 10, 11 і 12. Ширину зони у цьому разі знаходять із співвідношення: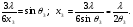

Отже, при інтерференції світла від кожної пари із сусідніх зон амплітуда результуючих коливань дорівнює нулю, оскільки вони в цілому викликають коливання з однаковими амплітудами, але протилежними фазами. Тому умову мінімуму інтерференції можна визначити, по – перше, за парним числом півхвиль, що вкладаються в різницю ходу між крайніми променями, а саме: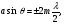

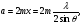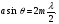де m= 1,2,3,…, а, по – друге, через парне число зон Френеля в щілині: або (6)

Встановимо геометричну умову для пучностей. У напрямі =0 спостерігається найінтенсивніший центральний максимум нульового порядку: коливання, що викликаються всіма ділянками щілини, здійснюються в однаковій фазі. Далі будемо міркувати так. Якщо різниця ходу між крайніми променями дорівнює , в щілині(отворі) вкладається дві зони, які компенсують одна одну, а якщо різниця ходу між крайніми променями дорівнює 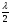, то в щілині(отворі) вкладається одна зона, яка нічим не компенсується. Це означає, що у випадку однієї зони різниця ходу ∆l між середнім і крайнім променями дорівнює 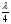, тобто 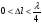(7)

Щілина (отвір) відкриває одну зону, й інтенсивність світла в центрі дифракційної картини в 4 рази більша, ніж за відсутності щілини (отвору). Перший побічний максимум повинен бути в напрямі між першим і другим дифракційними мінімумами і визначатися з умови 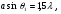тобто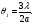

Тому різниця фази між сусідніми джерелами становить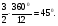

Відмітимо пари джерел, різниця фаз між якими становить 180°. Це такі: 1 і 5, 2 і 6, 3 і 7, 4 і 8. Оскільки джерела 5, 6, 7,8 уже скомпенсовані, залишаються не скомпенсованими джерела 9, 10, 11, 12. Таким чином, зона (1, 2, 3, 4) компенсується зоною (5, 6, 7, 8), а зона (9, 10, 11, 12) дає побічний максимум, інтенсивність якого становить 1/3 від інтенсивності всієї щілини. І в цьому разі дифракційний максимум першого порядку відповідає дії однієї зони (промені 9, 10, 11, 12). Аналогічно можна показати, що умови дифракційного максимуму запишуться через непарне число півхвиль, що вкладається в різниці ходу між крайніми променями, або через непарне число зон Френеля, що вміщуються у щілині: 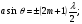(8)

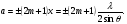(9)

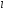
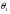
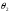
1

2

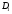
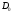
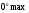
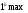
Рис. 8

Порівняємо ширину головного (нульового) максимуму на екрані із шириною наступних максимумів. Нехай 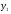- відстань від середини центрального (нульового) максимуму до першого мінімуму, а 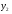- відстань від тієї ж середини центрального максимуму до другого мінімуму (Рис.8). Тоді 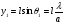, ширина головного максимуму становить 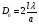, а ширина першого максимуму .

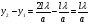Отже, ширина нульового максимуму інтенсивності 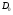при 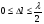вдвічі більша від наступних, перших максимумів, розміщених симетрично, тобто 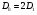. Із виразу для 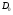видно, що червоне світло дифрагує сильніше, ніж синє.

2.2. Умови чіткого спостереження дифракції від однієї щілини

Характерною ознакою дифракції від щілини є те, що ширина нульового максимуму D_o на екрані вдвічі більша від наступних, перших максимумів, розміщених симетрично:

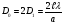, (10)

де 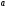- ширина щілини. Формула для обчислення інтенсивності світла на екрані від однієї щілини:

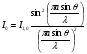(11)

Ми дотримуємось тієї позиції, що у широкому розумінні дифракція - сукупність явищ, зумовлених хвильовими властивостями світла, при яких порушуються закони геометричної оптики. Виділимо деякі з них.

Одним із явищ, які пояснюються на основі хвильової теорії, є прямолінійне поширення світла. Нехай від світної точки S світло поширюється у вигляді сферичної хвилі і доходить до точки А. За принципом Гюйгенса із точки А ми повинні бачити кожну точку сферичної хвилі. Однак цього не відбувається. Адже згідно із принципом Френеля коливання, які доходять до точки А від різних точок сферичної поверхні, взаємно знищуються, бо для кожної точки поверхні знайдеться інша точка, хід хвилі від якої до точки А відрізнятиметься на половину довжини хвилі, і вони гасяться. Отже, прямолінійне поширення світла належить до тих явищ, які можна пояснити, виходячи із принципу Гюйгенса-Френеля.

Зіставляючи явища дифракції та інтерференції, переконуємось, що дифракція завжди супроводжується інтерференцією, дифракція без інтерференції не існує (зворотне твердження справджується не завжди, оскільки інтерференція виникає не тільки завдяки дифракції, але і шляхом відбивання і заломлення світла). Цей зв`язок особливо проглядається, наприклад, в голографії.

Рис.9

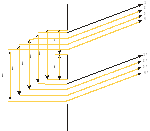
Закономірності дифракції від щілини та інтерференції від нескінченно тонких щілин дозволяють встановити дифракційні закономірності у дослідах з багатьма щілинами, включаючи дифракційну гратку. Максимум дифракції для двох щілин шириною 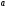, відстань між якими b, співпадає із умовою інтерференції для лінійних джерел 1 і 1`, 2 і 2` як нескінченно тонких щілин, елементів щілин шириною ,(рис 9):.

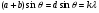(12)

У випадку нескінченно тонких щілин 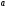0, тому інтерференційний максимум наступає, коли

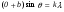(13)

Умова мінімуму для однієї щілини виконується для будь-якого числа щілин. Справді, якщо в даному напрямку від однієї щілини світла немає (рис.5), то і для будь-якого їх числа світла не буде. При спостереженні інтерференції внаслідок дифракції від двох щілин у кожному із дифракційних максимумів чітко проглядаються інтерференційні смуги, як на рис.4. Наведемо формулу розподілу інтенсивності світла у дифракційній картині від двох щілин, яка складається із двох множників - дифракційного (формула (5)) та інтерференційного (формула (2)):

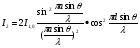(14)

При збільшенні числа щілин ширина дифракційних максимумів звужується, завдяки чому можна точніше виміряти довжину світлової хвилі за дифракційними спектрами.

Отже, дифракція спостерігається, коли ширина щілини набагато менша від ширини головного максимуму на екрані, тобто коли 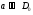: 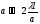, або .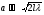

Останній вираз є допустимою умовою спостереження дифракції; вона залежить від співвідношення довжини хвилі 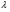, розмірів щілини (отвору) і відстані від неї до місця спостереження. Нагадаємо, що необхідною умовою спостереження дифракції є наявність просторового когерентного джерела світла.

Дифракція не спостерігається, якщо ширина головного максимуму мало відрізняється від ширини щілини (отвору), тобто коли 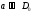. У цьому разі використовують наближення геометричної оптики. Ширина щілини, за якої на екрані спостерігається найвужча смужка світла. .

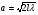Розділ 3.

Дифракційна природа оптичного зображення

3.1. Критерій Релея

Дослід Аббе свідчить про дифракційну природу оптичного зображення, якщо на капронову сітку направляти розширений пучок лазерного випромінювання на екрані спостерігають її зображення. Потім за сіткою встановлюють лінзу з фокусною відстанню F=50 мм. В фокусі цієї лінзи вертикально розміщують щілину. При зменшенні ширини щілини помічають, що вертикальні смуги на екрані зникають. Далі щілину встановлюємо горизонтально. Наслідком цього є поява на екрані вертикальних смуг. Якщо ж щілину поставити під кутом 45⁰ до горизонту, на екрані з’являться смуги під кутом 135⁰ до горизонту.

Які обмеження накладає хвильова природа світла на розрізнене сприймання двох джерел? Під роздільною здатністю оптичної системи розуміють її властивість давати роздільне зображення дрібних деталей об’єкта без порушення подібності їх предмету. Два точкових джерела сприймаються роздільно, якщо вони попадають, насамперед, на різні світлочутливі клітини на сітківці ока, роздільна здатність ока, в свою чергу, обмежується дифракційними явищами і зв`язана з розмірами зрачка. Зображення предметів складається із зображення сукупності точок і створюється за допомогою оптичних приладів. Вони складаються з оптичних деталей, розміри яких обмежені. Тому, наприклад, будь-який об`єктив, по суті, слугує дифракційним отвором.

У відповідності з двома схемами спостереження дифракції розрізняють оптичні прилади, у яких зображення створюються незалежно від присутності людини, і прилади, що працюють разом з оком людини. В першому випадку приймачами світла можуть бути фотопластинки, фотоопори, екрани, на яких дістають дійсне зображення. У другому випадку приймачем світла є око людини, яке може сприймати уявне зображення. Щоб узгодити ці прилади, треба знати той єдиний критерій, за яким дані, одержані в дійсній і уявній картині, будуть співпадати.

Нехай ми спостерігаємо досить віддалені точкові джерела світла S₁ i S₂ (фари автомобіля, що наближається, або дві зірки, на які направили об`єктив телескопа) з такої відстані, що їх дифракційні картини майже перекриваються або перекривають одна одну так, що їх максимуми співпадають. Тоді точки S₁ i S₂ зливаються і роздільно не сприймаються. Навіть якщо вони і попадають на різні світлочутливі точки ока, ми не бачимо їх нарізно. При наближенні автомобіля наступає момент, коли ми можемо сказати, що бачимо не одне, а два зображення. Щоправда, для різних спостерігачів він наступає дещо по-різному.

Тому загальноприйнятим став критерій розділення Релея. Він стосується в однаковій мірі всіх приладів, бо зумовлюється роздільною здатністю ока. Дві точки ми бачимо нарізно, якщо вони сприймаються різними світлочутливими клітинами на сітківці ока, а це наступає, коли, як встановив Релей, центр дифракційного диска однієї співпадає з мінімумом на дифракційній картині другої. Іншими словами, умовою або межею розділення (можливості бачити нарізно) стала кутова півширина першого мінімуму дифракції від щілини (3) і отвору ( ). На розділення двох джерел не впливає зміна їх розмірів, якщо мінімальна відстань між ними підтримується постійною: роздільна здатність визначається дифракцією світла від внутрішніх шарів. Тим самим, дифракція обмежує збільшення оптичними приладами, бо в межах 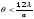будь-яке збільшення означає лише збільшення дифракційної картини без збереження подібності об`єкта. Однак, хоча дифракція обмежує збільшення і роздільну здатність, завдяки їй установлюється чітка межа розділення дифракційних зображень оптичними приладами.

3.2. Роздільна здатність мікроскопа і телескопа

Ми розглянули критерій Релея, який дає змогу розрізнити предмети за їх дифракційними зображеннями, не торкаючись питання про те, як утворюються зображення самих предметів. Критерій Релея в однаковій мірі відноситься до всіх оптичних приладів, основне призначення яких полягає у створенні зображень предметів, і стосується самосвітних і освітлювальних об’єктів. Теорію роздільної здатності для мікроскопа розробив німецький учений Ернст Аббе (1840-1905), який указав на різницю між утворенням зображення освітлених точок, і тих, що світяться. Завдяки його працям і діяльності організатора оптичного виробництва Карла Цейса (1816-1888) інструментальний арсенал оптики вийшов на той рівень, який відомий нам і сьогодні. Що нового приносить теорія Аббе до критерію Релея? Коротко про це можна сказати так. Для того , щоб розрізнити дві світні некогерентні точки в телескопі, достатня участь променів нульового максимуму, а щоб побачити дві освітлювані когерентні точки в мікроскопі, необхідна участь принаймні і променів першого максимуму.

Якщо для ока і телескопа мінімальна кутова відстань між точками, які можуть бути розділені як окремі, становить , то при тій же кутовій відстані точок у мікроскопі ми їх не побачимо, поки кожна з них, просто кажучи, не утворить у ньому зображення. Пояснити це означає вияснити:

1. за рахунок чого утворюється зображення предметів у мікроскопі;

2. як забезпечити подібність зображення його об’єкту.

Згадаймо, як утворюється зображення світних точок за законами геометричної оптики (рис. 10). Нехай точки А, В, С від об’ємного джерела, спряжені з екраном (друге положення екрана). Якщо пересунути екран вліво в перше положення (або наблизити їх до екрана), точки відобразяться у вигляді розмитих кружечків. На шляху променів установлюють діафрагму. Очевидно, що зменшуючи діаметр діафрагми, можна

Рис. 10

зменшити кружечки до розмірів, коли вони будуть здаватися для ока точковими – зображення стане чітким.

Однак геометрична оптика не в змозі пояснити утворення зображень у мікроскопі. В мікроскопі ми насправді спостерігаємо тінь від предметів. Унаслідок огинання світлом малої перешкоди ми її не бачимо, бо дифраговані промені не доходять до екрану, і тінь не утворюється, яке б велике збільшення ми не здійснювали.

За допомогою мікроскопа розглядають об’єкти, освітлені прохідним світлом. Але освітлені точки освітлюються одним і тим же точковим джерелом. Тому хвилі від них когерентні і шляхом дифракції (огинання) чи відбивання вони, з’єднуючись, інтерферують як і в інтерференційній (дифракційній) гратці, даючи світло чи темряву в залежності від різниці ходу. Тому освітлені об’єкти можна розглядати як дифракційну гратку, період якої дорівнює характерному розміру деталей об’єкта.

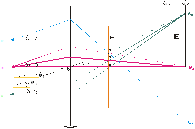
На рис. 11 схематично поданий випадок, коли на деталях об’єкта (

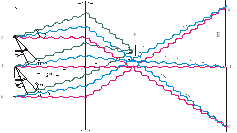
точки А, В, С) когерентні хвилі зазнають розсіяння (дифракція) і виходять під кутами, які задовольняють умові 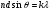, де n – показник заломлення середовища, d – характерний розмір деталей об’єкта (або дифракційної гратки ), який визначає кут дифракції 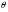; k=0,1,2… - порядок максимуму. Далі вони, у відповідності з принципом Гюйгенса-Френеля попарно інтерферують і в точках 0, 1, 2 утворюють дифракційні максимуми точок А, В, С (первинне, як назвав його Аббе, зображення). Вторинне зображення кожної із точок на спряженій площині (екран Е) утворюється внаслідок взаємодії променів від усіх 0, 1, 2 максимумів первинного або дифракційного зображення.

Якщо спробувати збільшити різкість зображення і з допомогою діафрагми або щілини перекрити побічні максимуми, вторинне зображення на екрані зникне. Нема дифракції - нема зображення. Отже, зображення має дифракційну природу. Дифракція – явище, яке забезпечує зображення предметів.

Для одержання зображень, цілком подібних об’єкту, треба, щоб у його створенні брали участь промені, які йдуть від усіх дифракційних максимумів. Особливе значення мають максимуми перших порядків. Вони розміщені під малими кутами і зумовлені великими, більш значними деталями об’єкта. При обмеженні числа максимумів різкість зображення втрачається.

Але дифракційні максимуми, як первинні зображення точок, утворюються завдяки тому, що дифраговані пучки перетворюються у збіжні лінзою об’єктива.

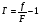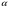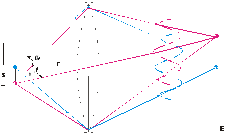
Для цього об’єкт якомога ближче розміщують до короткофокусного об’єктива мікроскопа (короткофокусний об’єктив дає більше збільшення, ніж довгофокусний, бо ). Чим ближче деталь до об’єктива, тим більшим буде кут, обмежений променями, які беруть участь у зображенні, тим більше променів створюють зображення. Прийнято говорити, що при цьому зростає апертурний кут . Кут 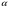, під яким із досліджуваної точки видно радіус лінзи, називають апертурним (це кут між віссю об’єктива і крайніми променями). З рис. 12 видно, що

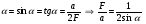, (15)

де 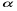- апертурний кут, 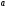- діаметр лінзи.

Разом з тим чим менший предмет, тим більше відхилення світла від прямолінійного поширення, тим більший кут дифракції 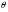він зумовлює.

Якщо апертурний кут 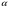об’єктива перевищує кут розходження 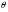, при якому в зображенні предмета беруть участь хоча б промені першого максимуму, зображення буде геометрично подібним до предмета. Під роздільною здатністю мікроскопа розуміють істинну відстань s між двома точками, які тільки-тільки вдається розділити:

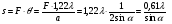(16)

Перш ніж розділити дві точки, треба забезпечити їх зображення. У формулі (16) 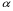- апертурний кут, який охоплює дифраговані пучки, побічних максимумів, що створюють зображення; 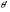- кут, при якому ми бачимо дві точки розділеними. Формула водночас визначає умови зображення і розділення точок.

Якщо між препаратом і об’єктивом внести краплину кедрового масла, показник заломлення якого 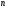, то відстань 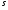зменшується, а, отже, роздільна здатність мікроскопа збільшується. Справді, чим більший показник заломлення, тим менший кут заломлення світла, і при тому ж апертурному куті у створенні зображення точки будуть брати участь максимуми більших порядків. Тому

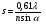(17)

3.3 Дифракційна гратка

Традиційно вивченню дифракційної гратки передує розгляд питання про інтерференцію в тонких плівках, когерентні промені від яких утворюються завдяки поділу амплітуди світлового пучка. Інтерференція від прозорих діелектричних прошарків відноситься до інтерференції від протяжних джерел, і відповідний навчальний матеріал не може бути пропедевтичним до пояснення дії дифракційної гратки. Справді, покладемо дифракційну гратку на кодоскоп і спроектуємо її зображення на екран або ж будемо розглядати світло від електричної лампи через решітку. Ніякої дифракційної картини ми не побачимо, бо світло від різних ділянок великого джерела не має властивості просторової когерентності.

Поставимо на шляху променів, що падають на дифракційну гратку, щілину. На екрані з’явиться дифракційний спектр. Отже, необхідною умовою виникнення дифракційних спектрів є наявність когерентних джерел світла у вигляді вузьких щілин.

Дифракційні гратки самі складаються із системи щілин шириною 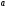і розділених непрозорими проміжками завширшки 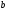. Пропускаючи когерентне світло, дифракційні спектри, інтенсивність світла в будь-якій точці екрана визначається результатом інтерференції дифракційних когерентних вторинних хвиль, які поширюються від різних ділянок однієї щілини і від різних щілин. Тому щілину не можна вважати нескінченною точкою.

Вивчення будь-якої складної системи спрощується, якщо розділити її на складові частини і вивчати кожну частину окремо.

Оскільки дифракційна гратка – це сукупність подвійних щілин, розміщених одна за одною, а кожну пару широких щілин можна зобразити як сукупність відповідних еквівалентних вузьких ділянок цих щілин, то в якості складової або “найпростішої комірки” дифракційної гратки можуть виступати дві вузькі щілини, відстань між якими 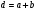, розмірами яких нехтують. Тому аналіз явища дифракції від двох широких щілин, а отже, і гратки, нагадує, по-перше, аналізінтерференційної картини від двох нескінченно тонких щілин за схемою Юнга, коли .

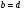Нагадаємо картину інтерференції від двох вузьких щілин (Рис. 4). Ширина смуг і їх інтенсивність однакова. Умова максимуму інтерференції виконується, коли

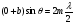(18),

бо 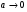, а умова мінімуму забезпечується, якщо різниця ходу

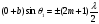(19)

У випадку, коли 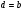, положення максимумів інтерференції від двох нескінченно тонких щілин (18) співпадають із положенням максимумів інтерференції від двох і багатьох щілин.

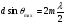(20)

де 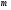- порядок дифракції спектру.

Отже, якщо в даному напрямі різниця ходу між кожною парою відповідних вузьких ділянок сусідніх щілин дорівнює цілому числу довжин хвиль, то від гратки в цілому буде спостерігатися в цьому напрямі дифракційний максимум. Інтерференційне підсилення дифракційних хвиль від відповідних нескінченно тонких щілин в такому випадку називають повним.

По-друге, елементом дифракційної гратки може бути сама щілина шириною 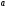, яку не можна назвати нескінченно тонкою, бо в цьому разі поза увагою залишається закономірність дифракції від щілини. Умова мінімуму для дифракційної гратки співпадає з умовою мінімуму для однієї щілини, бо якщо в даному напрямі від кожної щілини світла нема, то і від багатьох щілин світла не буде.

Якщо покласти на кодоскоп лист темного паперу із щілиною, на екрані одержимо чітке її зображення, а коли направити на ту ж щілину світло від іншої вузької щілини, можна спостерігати явище дифракції від щілини.

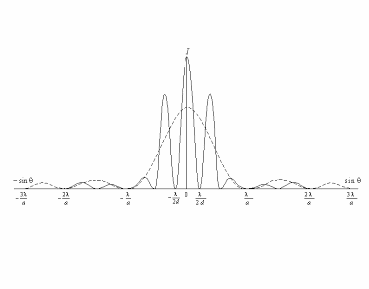
Картина дифракції від щілини і розподіл інтенсивності світла подані на мал. 4. Видно що між двома першими мінімумами розміщується нульовий дифракційний максимум ширина якого простягається від -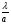 до +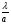, тобто вдвічі більша від наступних максимумів. Розподіл інтенсивності світла від однієї щілини описується залежністю:

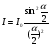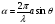, де (21)

Оскільки кожна щілина є елементом дифракційної гратки, нагадаємо закономірності дифракції від щілини, а також способи їх встановлення, з тим, щоб можна було поширити на дифракційну гратку. Умову мінімуму дифракції від щілини шириною 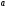в точці 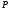екрана, різниця ходу до якої між крайніми променями щілини 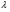, 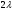і т. д., визначають за принципом Гюйгенса-Френеля. Однак вибір числа вторинних ідеальних джерел цілком довільний. Якщо таких джерел чотири, то хвилі від першого третього, другого і четвертого знаходяться у протифазі і їх дія компенсується. Різниця ходу між сусідніми променями 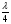, а різниця фаз 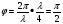. Коли вибрати шість джерел, то у протифазі знаходиться такі пари джерел, як: 1 і 3, 2 і 4, 3 і 6. різниця ходу між сусідніми хвилями 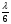, а різниця фаз 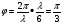. Виберемо 12 джерел. В цьому разі компенсується дія таких пар як 1 і 7, 2 і 8, 3 і 9, 4 і 10, 5 і 11, 6 і 12. Різниця ходу між сусідніми хвилями 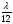, а різниця фаз .

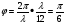Інтерференційне гасіння дифракційних хвиль від нескінченно тонких щілин кожної щілини, які знаходяться у протифазі, є повним.

Таким чином, незалежно від числа вторинних ідеальних джерел виконується закономірність: якщо різниця ходу між променями від крайніх джерел дорівнює 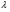, то має місце перший мінімум дифракції від щілини; коли різниця ходу між крайніми променями становить 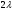, то у точці 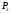буде другий дифракційний мінімум від щілини, і т. д., тобто

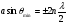, (22).

де 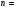1, 2, 3 ...

Розглянемо, чи залежить дифракційна картина від числа реальних щілин дифракційної гратки, якщо:

1. різниця ходу між променями від крайніх щілин дорівнює .

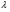2. різниця ходу між променями від крайніх щілин не дорівнює .

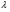Поширимо умову головних мінімумів для дифракції із однієї щілини на всю дифракційну гратку шириною 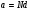, де 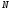число щілин, а 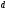- період дифракційної гратки

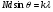(23)

де 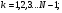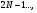бо, як показу аналіз формули, при 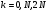вона перетворюється на умову головних максимумів (20). Оскільки 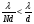, то 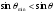, тобто між двома головними максимумами розміщується 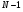побічних мінімуми.

Дві широкі щілини являють собою найпростішу дифракційну гратку. Положення двох сусідніх головних максимумів в дифракційній картині від них визначається кутовою півшириною 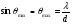. Кутова півширина кожного головного максимуму становить 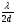і співпадає із умовою побічного мінімуму (23) в дифракційній картині від двох щілин, яка містить один побічний мінімум (k=1) у випадку чотирьох щілин кутова півширина головного максимуму зменшується і співпадає із умовою першого побічного мінімуму .

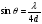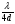
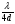
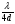
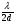
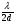
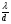
Рис. 14

Із Рис. 14 видно, що між головними максимумами з’являється 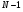побічний мінімум і 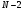побічних максимуми.

Таким чином, в залежності від числа щілин змінюється положення побічних мінімумів і положення побічних максимумів. Для тих променів, для яких різниця ходу 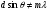, інтерференційне гасіння або підсилення дифрагованих хвиль від відповідних нескінченно тонких щілин може бути повним або неповним в залежності від числа щілин. Наведемо приклад. Нехай різниця ходу променів 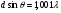. Тоді у випадку двох щілин відповідні хвилі дещо розійдуться за фазою, і між ними майже збережеться інтерференційне підсилення. У випадку величезного числа щілин різниця ходу променів, що виходять із двох сусідніх щілин, також невелика. Проте хвиля із однієї щілини може виявитись у протифазі із хвилею від іншої щілини, і їх суперпозиція приведе до інтерференційного гасіння. Тому максимуми стають вужчими, чим більше щілин має дифракційна гратка.

Оскільки ширина кожної щілини однакова, то, здавалось, дифракційна картина від двох щілин повинна бути такою, як і від однієї щілини. Проте це не так. Розподіл інтенсивності світла від двох щілин у випадку некогерентного і когерентного світла показаний на (Рис. 15) пунктирна крива відповідає додаванню інтенсивностей світла від обох щілин, якби їх освітлювати некогерентним світлом, а суцільно-когерентним.

Однак загальна інтенсивність світла, який пропорційний до площадок обмежених цими кривими і віссю абсцис, в обох випадках однакові. Дифракційну картину від двох щілин можна одержати, якщо інтерференційну картину від двох нескінченно тонких щілин моделювати функцію

Рис. 15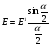

Оскільки 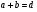, то 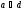, тому із формул видно що 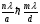, отже 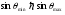. Головні максимуми (піки) лежать між головними мінімумами. Положення головних дифракційних максимумів і мінімумів при певній довжині хвилі залежить лише від періоду решітки і не залежить від структури періоду гратки і числа щілин. Між головними максимумами у випадку двох щілин знаходиться по одному побічному мінімуму, який визначається за формулою

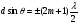(23)

Розглянемо, як позначається структура періоду найпростішої дифракційної гратки на характер дифракційної картини. Дослід показує що інтерференційний пік (максимум) 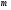порядку не спостерігається, коли він співпадає із першим дифракційним мінімумом. Із формули (20) і формули (22) при 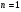, коли 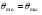допишемо: 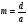. Отже порядок відсутнього інтерференційного максимуму і число інтерференційних смуг, які уміщуються в нульовому (центральному) дифракційному максимумі, залежить від структури періоду гратки, тобто від відношення 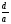і не залежить від довжини хвилі 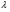. Нехай в центральному дифракційному максимумі спостерігається 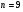смуг, тобто смуги при 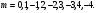Порядок відсутнього інтерференційного максимуму 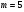. Його можна знайти також за формулою 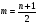. 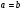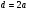Якщо , то і 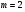. Всі парні головні максимуми при цьому не з’являються.

Висновки

Дифракція у широкому розумінні це сукупність явищ, зумовлених хвильовими властивостями світла, при яких порушуються закони геометричної оптики. Явище огинання світлом перешкод легко пояснити за допомогою відомого принципу Гюйгенса. На основі цього принципу можна встановити: 1) зображення світної точки у формі розмитого світного диска перевищує розміри отвору. 2) є підстава вважати, що точкові джерела освітлюють екран рівномірно.

Чим вужча щілина, тим більше відхилення світла від прямолінійного поширення. Якщо розміри щілини були меншими за довжину хвилі, вона напевно, рівномірно освітлювала б значну частину екрана. Завдяки дифракції приходимо до моделі лінійного (точкового) джерела світла. Якщо пропускати когерентне світло крізь невеликий отвір в екрані, потім направляти на два невеликі розміщені отвори в іншому екрані. Від кожного будуть виходити дифрагуючі конусоподібні когерентні пучки світла, що перекривають один одного і дають інтерференційну картину, ширина максимумів інтерференції та їх інтенсивність в центральній частині екрана однакові. Картина від щілини більш виразна, ніж від точкових джерел. Щілина – це, по суті, сукупність пар проколів (точкових джерел). Однак, насправді, при наближенні екрана до отвору дифракційне зображення окремої світної точки оточене темними кільцями.

Дифракція – це не просто огинання , це складне явище, яке не можна пояснити використовуючи лише принцип Гюйгенса. І тут на допомогу приходить принцип Гюйгенса-Френеля, згідно з яким щілина, якої досягає фронт хвилі, стає джерелом нових вторинних хвиль. Характерною ознакою дифракції від щілини є те, що ширина нульового максимуму на екрані вдвічі більша від наступних, перших максимумів, що розміщені симетрично.

Які обмеження накладає хвильова природа світла на розрізнене сприймання двох джерел? Два точкових джерела сприймаються роздільно, якщо вони попадають, насамперед, на різні світлочутливі клітини на сітківці ока, і як встановив Релей, центр дифракційного диска однієї співпадає з мінімумом на дифракційній картині другої. Іншими словами, умовою або межею розділення стала кутова півширина першого максимуму дифракції від щілини.

Критерій Релея в однаковій мірі відноситься до всіх оптичних приладів, основне призначення яких полягає у створенні зображень предметів і стосується самосвітних і освітлюваних об’єктів.

Ернст Аббе, вказав на різницю між утворенням зображення освітлених точок, і тих, що світяться. Якщо для ока і телескопа мінімальна кутова відстань між точками, які можуть бути розділені як окремі, становить 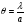, то при тій же кутовій відстані точок у мікроскопі ми їх не побачимо, поки кожна з них, просто кажучи, не утворить у ньому зображення. Для одержання зображень, цілком подібних об’єкту, треба щоб у його створенні брали участь промені, які йдуть від усіх побічних дифракційних максимумів.

Дослід Аббе свідчить про дифракційну природу оптичного зображення, якщо на капронову сітку направляти розширений пучок лазерного випромінювання на екрані спостерігають її зображення. Потім за сіткою встановлюють лінзу з фокусною відстанню F=50 мм. В фокусі цієї лінзи вертикально розміщують щілину. При зменшенні ширини щілини помічають, що вертикальні смуги на екрані зникають. Далі щілину встановлюємо горизонтально. Наслідком цього є поява на екрані вертикальних смуг. Якщо ж щілину поставити під кутом 45⁰ до горизонту, на екрані з’являться смуги під кутом 135⁰ до горизонту.

Отже: 1) дифракція – це огинання світлом перешкод.

2) дифракція – це інтерференція дифрагуючих променів.

3) дифракційна природа оптичного зображення (дослід Аббе).

Список використаних джерел

1. Васильев А. Эрнест Аббе и “Карл Цейс Йена” // Квант. – 2000. – №1. – С. 17-19.

2. Гончаренко С. У. Фізика 11. – К.: Освіта, 1995. – 448 с.

3. Єнін В. М. Савченко В. І. Єдиний підхід до вивчення хвильових властивостей світла // Збірник наукових праць Кам’янець-Подільського педагогічного університету. – Вип. 5. – 1999. – С. 125-138.

4. Резников Л. И. Физическая оптика в средней школе. – М.: Просвещение, 1971. – 264 с.

5. Стасенко А. Пределы зоркости приборов // Квант. – 2000. – №3. – С. 39-41.

6. Физика. Оптика и волны. 4. II. // Под ред. А. С. Ахматова.- М.: Наука, 1974.- 400с.

7. Калитеевский Н. И. Волновая оптика // Наука, 1971. – 376с.

8. Бабенко О. К. Методика викладання коливальних і хвильових явищ у середній школі // Радянська школа, 1958. – 362с.

9. Корсак К. В. Фізика: 25 повторювальних лекцій: Навч. Посібник. – К.: Вища шк.., 1994. – 431с.

10. Підвищення ефективності уроків з фізики. / за ред. Бугайова О.І. – К.: Радянська школа, 1986 – 152с.

11. Гончаренко С. У. Фізика: проб. навч. пос. для 11 кл. Шк.. III ступ., гімназій і ліцеїв гумуніт. проф.. – 2-ге видання – К.: Освіта, 1998. – 287с.

12. Ландсберг Г. С. Оптика - М., 1976 г. 928 с.

13. Шахмаев Н. М и др.. Фізика: учеб для 11 кл серед шк../Н. М. Шахмаев, С. Н. Шахмаев, Д. Ш. Шодиев. – М. : Просвещение, 1991. 239 с.

14. Ярошевский М.Г., Зорина Л.Я. История науки и школьное обучение. – М.: Знание, 1978. – 190с.

15. Кононов В. М. Об изучении дифракционной решетки. – Физика в школе. - №1, 2001, с. 29-30.