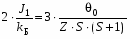
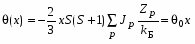
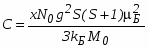
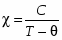
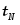
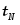
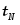
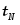
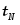
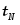
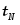
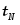
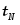
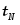
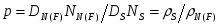
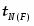
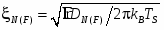
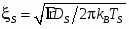
Реферат

Влияние граничных условий на критическую температуру неоднородных сверхпроводящих мезоструктур

Исследования неоднородных сверхпроводящих мезоструктур, в которых сверхпроводимость обусловлена наличием эффекта близости, представляют большой интерес как с прикладной, так и с фундаментальной точек зрения.

В данной работе рассматривается проблема влияния внешних границ на критическую температуру структур типа сверхпроводник/нормальный металл (S/N) и сверхпроводник/ферромагнетик (S/F). В качестве структур типа S/N были рассмотрены трехслойные образцы вида N/S/N и S/N/S. В качестве структур S/F типа исследовались бислойные S/F структуры.

Измерения для многослойных структур S/N типа проводились на трехслойных образцах Cu/Nb/Cu и Nb/Cu/Nb, детали приготовления приведены в [1]. Измерения для структур S/F типа были выполнены на образцах Nb/PdNi детали приготовления описаны в [2].

Критические состояния для структур типа S/F и S/N в отсутствии внешнего магнитного поля без учета парамагнитного и спин-орбитального взаимодействия, могут быть описаны с помощью уравнений Узаделя [3]. В качестве условий сшивания на плоскостях контакта сверхпроводящего и несверхпроводящего слоев использовались условия Куприянова - Лукичева [4]. Метод решения приведен в [5].

Из [5] следует, что решение граничной задачи зависит от следующих параметров. Для S/N структур – от критической температуры массивного сверхпроводящего материала (Nb) T_S, частоты Дебая _D, длин когерентности в сверхпроводящем и несверхпроводящем слоях:

,

,

где D_S, D_N(F) – постоянные диффузии сверхпроводящего и нормального (ферромагнитного) металлов; параметра прозрачности S/N(F) границы , и параметра

,

где _S, _N(F) – низкотемпературные (при T = 10 K) удельные сопротивления сверхпроводящего и нормального (ферромагнитного) металлов, соответственно. В случае S/F структур, кроме указанных выше параметров, подгоночным также оказывается еще один параметр – энергия обменного взаимодействия E_ex.

Дебаевская частота, являясь параметром обрезания, должна быть достаточно большой, чтобы не влиять на критические характеристики сверхпроводника. Это условие с большим запасом выполняется для исследуемых материалов. В частности, для Nb _D = 275 K. Для определения длины когерентности трехслойных S/N структур _S = 6.4 нм были выполнены отдельные измерения H_c2(T). Для бислойных S/F структур получено _S = 6 нм [2].

Значение параметра p = 2.77 в рассматриваемом экспериментальном случае для Cu/Nb/Cu определяется вполне однозначно. Для структуры Nb/Cu/Nb оказывается возможным получить лишь оценку, p  2.0 – 8.5. Для структуры Nb/PdNi согласно [2] – p  0.1 – 1.29.

Параметр T_S достаточно уверенно можно задать для N/S/N, сравнивая асимптотики экспериментальной и теоретической зависимостей T_c(d_S); в результате для Cu/Nb/Cu имеем T_S  9 K. Для Nb/Cu/Nb можно установить лишь интервал допустимых значений 7.5 K < T_S < 9.2 K. Для Nb/PdNi из асимптотического значения T_c(d_S) при T_c→ ∞ получено - T_S  8.8 K. Для структуры Nb/PdNi согласно [2] получено значение E_ex = 230 К.

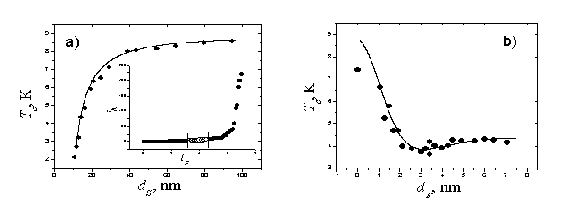
Параметры и _N для структуры N/S/N функционально связаны т.е. существует кривая (_N), все точки которой дают одну и ту же зависимость T_c(d_S) (вставка к рисунку 1a). На рисунке 1a белыми квадратами представлена зависимость, рассчитанная со значениями подгоночных параметров T_S = 9 K, _S = 6.4 нм, p = 2.77, = 0.98, _N = 34 нм, экспериментальные данные обозначены черными точками.

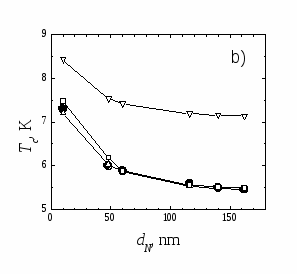
Попытаемся теперь воспроизвести экспериментальную зависимость (черные точки на рис. 1b) T_c(d_N) для структуры Nb/Cu/Nb с набором параметров, определенных в задаче о восстановлении зависимости T_c(d_S). Оказывается, что при заданных p = 2.77, T_S = 9 K не существует значений (,_N), воспроизводящих экспериментальную зависимость T_c(d_N). На рисунке 1b треугольниками острием вниз представлена теоретическая кривая T_c(d_N), построенная по параметрам = 0.98, _N = 34 нм, – видим полное несоответствие экспериментальным данным по структуре Nb/Cu/Nb. Воспроизвести экспериментальную зависимость T_c(d_N) возможно, одновременно изменяя значения подгоночных параметров p, T_S. На рисунке 1b треугольниками острием вверх показана кривая, рассчитанная со значениями подгоночных параметров = 0.98, _N = 34 нм, p = 2.77, характеризующих структуру Cu/Nb/Cu, и при T_S = 8 K; однако хорошее согласие теории и эксперимента достигается при этом существенным изменением длины когерентности: _S = 8 нм. На том же рисунке белыми квадратами обозначена теоретическая зависимость T_c(d_N), рассчитанная с параметрами структуры Cu/Nb/Cu _S = 6.4 нм, = 0.98, _N = 34 нм, и T_S = 9 K, и с подгонкой параметра p; его значение, p = 9.8, выходит за границы интервала допустимых значений. Был получен также набор возможных значений параметров (T_S, p), восстанавливающий зависимость T_c(d_N) для S/N/S структур.

Рисунок 1. Зависимости T_c(d_S) (a) и T_c(d_N) (b) для трехслойных S/N структур.

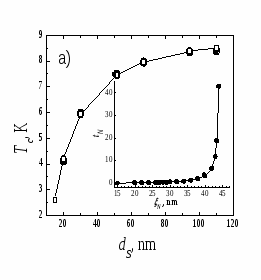
На рисунке 2a линией обозначена теоретическая зависимость T_c(d_S) для бислойных S/F структур, рассчитанная со значениями подгоночных параметров: E_ex = 230 К, T_S = 8.8 K, _S = 6 нм, p = 0.29, =3.2, l_F = 4 нм, где l_F – длина свободного пробега электрона в ферромагнитном слое, экспериментальные данные обозначены черными точками. Зафиксировав первые четыре параметра, можно получить набор параметров (, l_F), значения которых восстанавливают зависимость T_c(d_S) (вставка к рис. 2a, черные точки). На рисунке 2b линией изображена теоретическая зависимость T_c(d_F), экспериментальные данные – черные точки. Область значений возможных подгоночных параметров (, l_F) восстанавливающих зависимость T_c(d_F) выделена на вставке к рис. 2a (белые точки).

Рисунок 2. Зависимости T_c(d_S) (a) и T_c(d_F) (b) для бислойных S/F структур.

Полученное различие в материальных параметрах, описывающих свойства S/N/S и N/S/N структур, в первую очередь обусловлено различием свойств внутреннего S слоя в Cu/Nb/Cu и внешних S слоев в Nb/Cu/Nb образцах. Неоднородность внешних поверхностей структуры S/N/S оказывает сильное влияние на ее характеристики. Фактически вместо трехслойной S/N/S мы имеем пятислойную многослойную структуру S/S/N/S/S, в которой свойства внешнего слоя S точно не известны, и могут изменяться неконтролируемым образом для разных образцов. С практической точки зрения это значит, что для идентификации параметров многослойных структур вида N/S/…/S/N нельзя использовать S/N/S-структуры. Понятен способ преодоления этих сложностей: вместо структур S/N/S следует использовать структуры N/S/N/S/N. Расчеты, проведенные для структур S/F типа полностью подтверждают результат, полученный для структур типа S/N/S и N/S/N. Т.е. в случае бислойных структур Nb/PdNi набор значений подгоночных параметров, восстанавливающих зависимость T_c(d_F), полностью входит в диапазон значений подгоночных параметров для T_c(d_S).

Воздействие концентрированных потоков энергии на материалы является на сегодняшний день активно изучаемым вопросом физики твердого тела и физического материаловедения [1]. Среди широкого спектра различного вида высокоэнергетических воздействий особый интерес с точки зрения модифицирования структурно-фазового состояния и свойств приповерхностных слоев представляет воздействие компрессионными плазменными потоками. Особенностью энергетических потоков данного рода является сочетание квазистационарности воздействия и высокой плотности передаваемой энергии [2]. Обработка компрессионными плазменными потоками может проводиться на различного рода объектах, одним из которых является система «металлическое покрытие-кремниевая подложка». Наиболее важной научной и практической задачей является изучение возможости образования приповерхностных слоев силицидов металлов в результате плазменного воздействия, особенностей их состава и микроструктуры [3].

В настоящей работе исследовалась возможность силицидообразования в системе «никелевое покрытие-кремний» в результате воздействия компрессионных плазменных потоков, а также их структура и распределение в приповерхностном слое.

В качестве объекта исследования использовалась монокристаллическая пластина кремния (кристаллографическая ориентация (100)). Покрытие никеля толщиной 4 мкм наносилось методом химического осаждения. Согласно диаграмме состояния [4], в системе никель-кремний возможно образование ряда силицидов, обогащенных никелем (Ni₃Si, Ni₂Si, Ni₃₁Si₁₂, Ni₃Si₂), моносилицида NiSi и дисилицида NiSi₂.

Генерирование компрессионных плазменных потоков проводилось в магнитоплазменном компрессоре компактной геометрии. В качестве плазмообразующего вещества использовались азот (давление ~400 Па). Воздействие проводилось одним импульсом и серией из трех импульсов. Продолжительность импульса составляла ~100 мкс, давление потока – 1,5 МПа, температура – 3 эВ, плотность поглощенной энергии – 8-13 Дж/см².

Фазовый состав обработанной системы никель-кремний исследовался методом рентгеноструктурного анализа на дифрактометре ДРОН-4-13 при фокусировке по Брэггу-Брентано в излучении Cu Kα. Исследование элементного состава проводилось методом Оже-электронной спектроскопии на установке PHI-660 фирмы Perkin Elmer. Регистрация оже-электронов производилась при травлении образцов ионами аргона энергией 3 кВ. Микроструктура обработанной системы, а также планарное и латеральное распределение элементов изучались методом растровой электронной микроскопии и рентгеноспектрального микроанализа на микроскопе LEO1455VP фирмы “Karl Zeiss” с энергодисперсионным рентгеноспектральным микроанализатором Rontec.

Исследования элементного состава обработанной системы показали, что высокоэнергетическое плазменное воздействие приводит к перераспределению компонент покрытия и подложки. Увеличение количества импульсов вызывает более глубокое проникновение никеля. Согласно результатам фазового анализа, плазменная обработка ведет к образованию силицидов. При увеличении плотности энергии потока плазмы практически весь никель вступает в реакции силицидообразования вследствие более интенсивного перемешивания. В результате воздействия одним импульсом формируются силициды NiSi, NiSi₂, а в случае воздействия серией из трех импульсов – Ni₂Si, NiSi, NiSi₂. Совместное образование моно- и дисилицида никеля обусловлено их близкими энергиями образования (~85 кДж/моль), наиболее низкими среди всех силицидов никеля [5]. Формирование силицида Ni₂Si и увеличение глубины проникновения никеля при воздействии серией импульсов связано с интенсивным взаимным диффузионным перемешиванием никеля и кремния при каждом последующем плазменном импульсе.

Результаты исследования морфологии поверхности обработанных образцов и их поперечного сечения выявили, что микрорельеф характерен для быстрозатвердевшей жидкости. Таким образом, высокоэнергетическое воздействие компрессионного плазменного потока приводит к расплавлению покрытия никеля и части кремниевой подложки, перемешиванию их компонент за счет жидкофазной диффузии и конвекции. Толщина переплавленного слоя составляет 10-15 мкм.

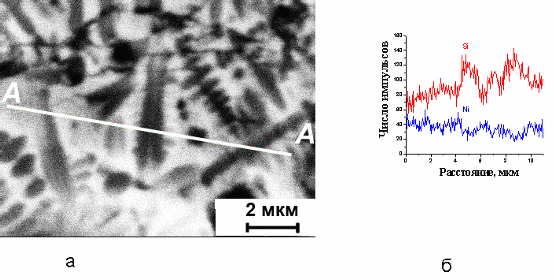
Рис.3 Микрофотография дендритной структуры (а) и распределения интенсивностей характеристических рентгеновских излучений кремния и никеля вдоль линии АА (б) системы Ni/Si(100), обработанной одним импульсом при плотности энергии потока 8 Дж/см²

В приповерхностном слое было обнаружено формирование дендритной структуры. Характерный размер дендритов составляет 2-20 мкм. Преимущественная ориентация дендритов соответствует направлению (100). Особенностью пространственного распределения элементов в дендритных областях является повышенное содержание кремния внутри дендритов (рис. 1). Формирование данного вида структуры описывается в рамках модели концентрационного переохлаждения [6]. При быстром затвердевании кремния происходит вытеснение никеля за границу кристаллизации. В результате этого образуется область жидкости, обогащенной никелем, которая, согласно диаграмме состояния, имеет меньшую температуру кристаллизации, т. е. имеет место переохлаждение. При этом любой случайный выступ на границе жидкой и твердой фаз, попадающий в область переохлажденной жидкости, становится устойчивым образованием и при дальнейшем развитии перерастает в дендрит. Ориентация дендритов, главным образом, определяется направлением движения фронта кристаллизации. Увеличение плотности энергии плазменного потока приводит к более интенсивному образованию дендритов ввиду увеличения градиента температуры и скорости кристаллизации. Рост дендрита сопровождается диффузией никеля за границу кристаллизации, вследствие чего в междендритных областях, закристаллизовавшихся позднее, концентрация никеля выше, чем внутри дендритов. В данных областях наиболее вероятно образование силицидов, обогащенных никелем, а также моносилицида, в то время как формирование дисилицида наиболее интенсивно происходит внутри дендритов, а также возле их границ.

Таким образом, было выявлено, что воздействие компрессионных плазменных потоков на систему «никелевое покрытие-кремний» приводит к перераспределению компонент покрытия и подложки в приповерхностном слое толщиной 10-15 мкм, формированию силицидов никеля Ni₂Si, NiSi, NiSi₂, а также к образованию дендритной структуры с характерным размером ветвей 2-20 мкм. Установлено, что при воздействии импульса компрессионной плазмы происходит расплавление покрытия никеля и части кремниевой подложки, жидкофазное перемешивание и быстрая кристаллизация, сопровождаемая концентрационным переохлаждением.

Твердые растворы Hg_1-xMn_xS должны быть полупроводниками со сменной в зависимости от состава шириной запрещенной зоны (E_g) и принадлежат к полумагнитным полупроводникам. Наличие в кристаллах атомов Mn с нескомпенсированным магнитным моментом дает возможность контролировать состав (х) и наличие в образцах включений второй фазы магнитными методами (в частности с помощью измерений магнитной восприимчивости кристаллов).

Полумагнитные полупроводниковые твердые растворы Hg_1-xMn_xS (область существования которых (0<х≤0,375) [1]), полученные нами методом Бриджмена, владеют проводимостью n-типа (концентрация электронов n~10¹⁸см^-3).

Исследование магнитной восприимчивости (χ) образцов Hg_1-xMn_xS проведено методом Фарадея в интервале Т=77-300К и Н=0,25-4кЭ. Установлено, что зависимости χ_Mn^-1 = f(T)) состоят из прямолинейных участков, которые описываются законом Кюри или Кюри-Вейсса:

;(1)

где С – постоянная Кюри:

;(2)

Отрицательные значения парамагнитной температуры Кюри (θ<0) указывают на то, что в кристаллах Hg_1-xMn_xS между атомами Mn возникает обменное взаимодействие антиферромагнитного характера. Рассмотрим возможные типы включений второй фазы и кластеров (которые им соответствуют по характеру обменного взаимодействия, но в отличие от фаз не владеют собственной кристаллической структурой, а образуются в рамках кристаллической структуры кристалла, в котором они существуют) в кристаллах Hg_1-xMn_xS. К таким фазам, которые могли бы образоваться в исследуемых кристаллах, относятся MnS₂ (T_N=60K, = -592K), MnS (T_N=155K, = -982K), Mn (T_N=100K) (фаза MnО с T_N=120 K, или соответствующие ей кластеры менее вероятны, чем рассмотренные). Все эти фазы являются антиферромагнетиками и если бы они присутствовали в Hg_1-xMn_xS, то это привело бы к особенностям на температурной зависимости магнитной восприимчивости при указанных температурах Нееля (Т_N). В кластерах, которые отвечают этим фазам, обменное взаимодействие антиферромагнитного характера (антиферромагнитное упорядочение) проявляется слабее или сильнее, в зависимости от размеров кластеров и температуры. С увеличением размеров кластеров парамагнитная температура Кюри () и температура излома (Т_С) на зависимости χ_Mn^-1= f(T), которые их характеризуют, будут возрастать, приближаясь к соответствующим параметрам, которыми владеют соответствующие этим кластерам фазы: MnS₂, MnS, Mn, а при выделении этих фаз параметры совпадут. Так особенность на зависимостях χ= f(T) и χ_Mn^-1= f(T) для х_м=0,025 находится при Т~155К, что может свидетельствовать о наличии включения второй фазы (MnS) в кристалле Hg_1-xMn_xS.

Учитывая вышесказанное, можно допустить, что наиболее вероятными в кристаллах Hg_1-xMn_xS есть кластеры типа Mn-S-Mn-S, которые по характеру обменного взаимодействия подобны фазе MnS, поскольку образуются они в кристаллах Hg_1-xMn_xS в результате изовалентного замещение атомами Mn атомов ртути.

Таким образом наличие изломов на зависимостях χ_Mn^-1= f(T) (при Т=Т_С) обусловлено переходом в парамагнитное состояние при повышении температуры кластеров типа Mn-S-Mn-S (разного размера), в которых между атомами Mn через атомы серы осуществляется непрямое обменное взаимодействие антиферромагнитного характера (аналогично, как в Hg_1-xMn_xSе [2, 3]). Увеличение эффективного магнитного момента (μ_эф.) атомов Mn, при повышении температуры, подтверждает то, что при Т=Т_С кластеры переходят из “антиферромагнитного” в парамагнитное состояние (табл. 1).

Таблица 1.

Магнитные параметры образцов Hg_1-xMn_xS

х_м.

θ, К

μ_эф.(μ_Б)

Т_С, К

0,017

0

5,92

–

0,046

-12

-63

5,05

6,05

125

0,069

-15

-85

4,81

5,90

135

Экстраполяция до нуля усредненных в области высоких температур зависимостей χ_Mn^-1=f(T), которые описываются законом Кюри–Вейсса, дает значение  для образца с составом “х_м”, полученным на основе зависимостей χ_Mn^-1=f(T) и формул (1, 2).

Авторы работы [4] в рамках высокотемпературного приближения (k_БТ>>_A, где _A) – энергия обменного взаимодействия между атомами, которые владеют собственными магнитными моментами) получили такое выражение для величины парамагнитной температуры Кюри:

,(3)

где J_p – интеграл обменного взаимодействия для пары соседей, Z_p – количество катионных состояний в р- координационной сфере. Константа ₀ отвечает предельной величине (х) для гипотетического магнитного полупроводника с х=1 и структурой полупроводников типа А^ІІВ^VI.

Выражение (3) разрешает определить величину обменного интеграла (J₁) пары соседей в первой координационной сфере (Z=12):

(4)

Экспериментальная зависимость (х), которая получена для Hg_1-xMn_xS является прямой линией. Экстраполяция этой зависимости к х= 1 дает ₀= – 990К. Полученное значение ₀ разрешает определить величину обменного интеграла (для пар Mn–S–Mn) J₁/k_Б=-14,1К.

В таблице 1 приведены параметры, которые определены на основе полученных χ_Mn^-1=f(T) для образцов Hg_1-xMn_xS, а именно: содержание магнитной компоненты (х_м) (полученое на основе “усредненных” высокотемпературных участков χ_Mn^-1=f(T) при Т~300К), парамагнитная температура Кюри (θ), температура излома (Т_С), значение эффективного магнитного момента атомов марганца (μ_эф). Для данного х_м нижняя строка параметров относится к более высокотемпературному участку зависимости χ_Mn^-1=f(T).

При термообработке кристаллов Hg_1-xMn_xS, которые владеют довольно выраженной как дефектной, так и кластерной подсистемами, создаются возможности для диффузии в кристалл атомов паров компонент (при отжиге) и вырывания из узлов и миграции атомов по кристаллу и занятия ими разных мест в кристаллической решетке: вакансий, междоузлий, узлов.

Дефектная система в этом случае может способствовать как уменьшению, так и увеличению размеров кластеров и образованию новых кластеров, что проявляется как в изменении кинетических коэффициентов кристаллов (дефекты – электрически активные), так и в изменении магнитных параметров образцов (парамагнитной температуры Кюри () и эффективного магнитного момента атомов марганца (_эф.)) (табл. 2), а значит и зависимостей χ_Mn^-1=f(T), на основе которых они определяются.

Таблица 2.

Магнитные параметры образцов Hg_1-xMn_xS

x_м

n, см^-3 (при Т=300К)

θ, К

µ_эф, µ_Б (на атом Мn)

до отжига

после отжига

до отжига

после отжига

до отжига

после отжига

0,025

до и после отжига в парах ртути

8,6۠۠۠∙ 10¹⁷

1,2∙ 10¹⁸

-15

-29

-18

-54

5,08

5,75

5,41

6,03

0,046

до и после отжига в парах серы

8,7۠۠۠∙ 10¹⁷

3,1∙ 10¹⁷

-12

-63

-30

-146

4,96

5,95

5,01

6,31

Таким образом термообработка образцов в парах компонент приводит к изменению размеров существующих в кристалле кластеров (размеры кластеров пропорциональные величине θ) и даже к “рассасыванию ” включений второй фазы (т.е. к уменьшению их размеров и преобразованию включений второй фазы MnS в кластеры Mn-S-Mn-S).

Исследование кинетических коэффициентов кристаллов проведены в интервале Т=77-300К и Н=0,5-6 кЭ. Коэффициент Холла (R_H) в исследуемых кристаллах почти не зависит от температуры, что указывает на вырождение электронного газа. Электропроводность (σ) кристаллов имеет металлический характер (т.е. уменьшается с ростом температуры), что обусловлено уменьшением подвижности электронов (μ_Н) при увеличении Т. Термо-эдс (α) увеличивается с ростом температуры, что обусловлено уменьшением вырождения электронного газа.

Термообработка образцов Hg_1-xMn_xS в парах серы приводит к понижению концентрации электронов и увеличению их подвижности, а отжиг в парах ртути увеличивает концентрацию электронов в образцах.

Литература

1. В. А. Грибков, Ф. И. Григорьев, Б. А. Калин, В. Л. Якушин. Перспективные радиационно-пучковые технологии обработки материалов. Круглый год, М. (2001). 528 с.

2. В. М. Асташинский, В. В. Ефремов, Е. А. Костюкевич, А. М. Кузьмицкий, Л. Я. Минько.Физика плазмы 17 (1991). С. 1111-1115.

3. В. В. Углов, В. М. Анищик, Ю. А. Петухов, В. М. Асташинский, А. М. Кузьмицкий, Н. Т. Квасов. / 5^th International Conference “New Electrical and Electronic Technology and their Industrial Implementation”, Zakopane, Poland (2007). P.63

4. Диаграммы состояния двойных металлических систем. Т. 3, Кн. 1 / Под ред. Н. П. Лякишева. Машиностроение, М. (1997). 576 с.

5. Мьюрарка Ш. Силициды для СБИС. Мир, М. (1982). 176 с.

6. Вайнгард У. Введение в физику кристаллизации металлов. Мир, М. (1967). 160 с.