- 1 -

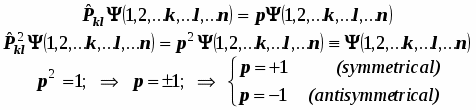
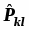
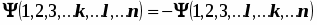
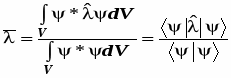
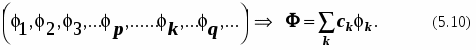
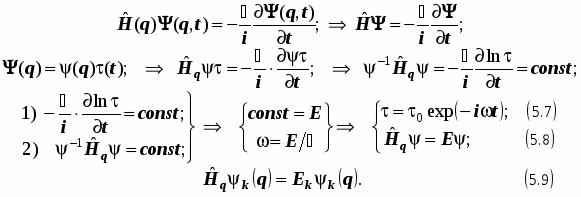
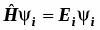
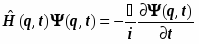
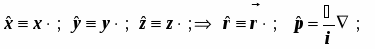
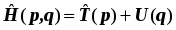
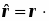
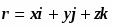
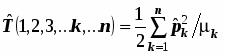
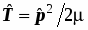
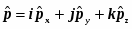
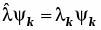
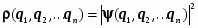
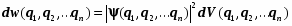
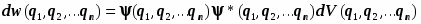
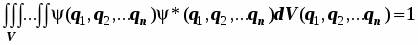
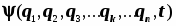
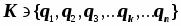
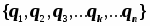
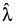
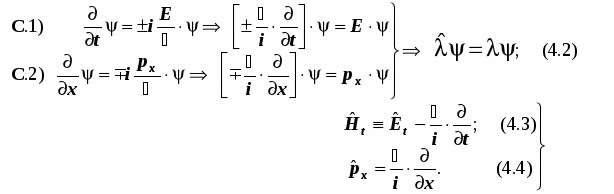
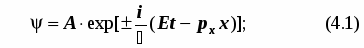
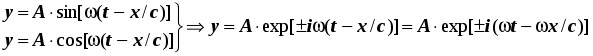
Введение в аксиоматику квантовой механики

Происхождение операторов динамических величин

Содержание:

Уравнение плоской бегущей волны материи.

Операторы импульса и энергии.

Общая схема вычислений физических наблюдаемых в квантовой механике.

4.1. Уравнение плоской бегущей волны материи

Для построения математической схемы квантовой механики необходимо расширить представления о волнах материи. Волны Де Бройля позволяет наиболее экономно показать, как появляются на свет Божий операторы импульса (p) и полной энергии (H), поясняя, что же это такое - операторные уравнения на собственные значения и их смысл. Однако показать – вовсе не означает доказать! ... Обратимся к цепочке рассуждений...

4.1.1. Плоская световая волна

(элекромагнитное поле) описывается уравнениями:

4.1.2. Плоская волна материи:

1. Подстановки E = ћ = mc² ;   = mc²/ћ = pc/ћ;   = E/ћ приводят к формуле

плоской волны материи:

Это выражение называется волновой функцией системы (плоской волны материи). Она зависит от двух переменных - времени и координаты. Волновая функция считается универсальным источником динамической информации о системе.

Это напоминает термодинамику. Посредством определённых преобразований и действий над термодинамическими функциями состояния можно вычислить прочие термодинамические свойства. Аналогично в квантовой механике из волновой функции системы можно определёнными действиями можно извлечь все её динамические характеристики. Волновая функция является функцией квантово - механического состояния системы.

Энергия и импульс получаются из волновой функции с помощью дифференцирования по разным переменным – времени и координате. Общая схема вычисления представлена формулой 4.2.

Слева от знака равенства волновая функция  подвергается совокупности преобразований. Вся совокупность действий, извлекающих эту физическую величину, сгруппирована в один оператор, его символ. Справа от знака равенства результатом преобразований является она же () с точностью до численного множителя ; он-то и представляет собой численное значение искомой физической величины.

Резюме. Выражения 4.3 и 4.4 настолько важны, что без них было бы затруднительно построить математический аппарат квантовой механики.

4.2. О структуре операторного уравнения

Способ расчёта динамических переменных из волновой функции оказывается настолько общей, что затрагивает самые важные вопросы о способах человеческого познания. Итак предмет нашего исследования - операторное уравнение (4.2). Перечислим то, что представляется особо важным.

Содержание:

Общая схема расчётов динамических переменных и структура операторных уравнений квантовой механики. Эксперимент и теория. Измерения и уравнения. Объекты и образы. Система и прибор, волновая функция и оператор. Микросистема и макроприбор, структура операторов. Опыт и теория: информация и организация. Идеальный опыт и операторное уравнение.

Бросается в глаза, что весь алгоритм вычисления динамической переменной разделяется знаком равенства на две части. Такое имеет место в любых вычислениях, знак равенства обязателен при записи уравнений, но здесь активную роль играет само понятие преобразования – понятие оператора.

Все действия слева от знака равенства сгруппированы в один-единственный оператор. Он определяет всю программу действий для достижения результата.

Сам же результат представлен численным множителем справа от знака равенства.

В обеих частях равенства присутствует волновая функция. Слева она объект преобразования, справа - неизменный объект, не претерпевший изменений.

Все эти признаки допускают очень простую и наглядную интерпретацию, самым тесным образом отражающую способы познания человеком окружающего мира. Главное в ней понятие объекта и образа-отображения. В таком случае в нашем понимании важную роль играет каждая деталь...

4.3. Рассмотрим операторное уравнение как образ идеального эксперимента

Волновая функция это образ исследуемой микросистемы.

Оператор, действием которого извлекается искомая величина, есть образ макроскопического прибора, настроенного на измерение конкретной искомой физической величины.

Знак равенства разделяет эксперимент на два качественно разных этапа. Исходный, стартовый этап, предшествующий измерению, изображён выражением слева от знака равенства. На завершающем этапе достигается количественная информация о системе, получено численное значение измеренной величины (справа от знака равенства).

Волновая функция в эксперименте остаётся неизменной, и это отражает простейшее обязательное качество идеального опыта – измерение не должно изменять систему. Иначе невозможно идентифицировать итоги опыта, результат измерения нельзя отнести ни какой-либо конкретной ситуации, ни к какому-либо состоянию, и нельзя вообще сказать, к той ли системе вообще данный результат относится.

При такой точке зрения следует постулировать некоторый минимальный набор операторов и далее определить правило составления оператора любой сколь-угодно более сложной величины.

Раздел 5. Основные понятия и постулаты квантовой механики

Содержание:

Система постулатов квантовой механики.

5.0. Понятие о конфигурационном пространстве системы частиц

При описании механических движений в системе частиц с номерами: {1,2, 3, ... n}

могут быть использованы различные пространственные переменные (прямоугольные-декартовы, косоугольные, полярные (шаровые, цилиндрические или эллиптические). Их полная совокупность, достаточная для составления исчерпывающих уравнений механики в конкретной задаче, называется конфигурационным пространством K. Координаты могут быть декартовы {x₁, y₁, z₁, x₂, y₂, z₂, x₃, y₃, z₃, ... x_n, y_n, z_n}, или полярные, например, шаровые {r₁, ₁, ₁, r₂, ₂, ₂, r₃, ₃, ₃, ... r_n, _n, _n}, или любые другие - в общем виде: . Максимальная размерность конфигурационного пространства K равна 3n - утроенному числу частиц в системе. Принадлежность переменных к конфигурационному пространству можно указать с помощью символов - кванторов включения, например, в виде: .

5.1. Постулат 1. Волновая функция и её свойства (конечность, однозначность, непрерывность и нормировка).

Формулировка:

Всякое состояние квантово-механической системы описывается функцией со-стояния - волновой функцией, заданной на многообразии всех переменных конфи-гурационного пространства системы, и также времени:

Волновые функции обязаны удовлетворять нескольким математическим требованиям. Они должны быть: 1)конечны, 2)однозначны, 3)непрерывны, 4)нормированны, т.е.:

; (5.1)

Область интегрирования охватывает весь возможный диапазон значений каждой переменной во всём пространстве K. Вероятностный смысл волновой функции:

. (5.2)

Нормировка оказывается условием суммирования плотности вероятности во всём конфигурационном пространстве. Квадрат модуля волновой функции является плотностью вероятности, с которой физическая система, пребывая в том физическом состоянии, которое описывается волновой функцией , распределена по конфигурационному пространству. Функции, отвечающие условиям 1, 2, 3 называются регулярными.

Волновая функция это математический образ квантово-механического состояния физической системы. Конечно же, это функция механического состояния системы.

5.2. Постулат 2. Измерения физических величин и операторные уравнения на собст-венные значения эрмитовых операторов

Формулировка:

Разрешёнными значениями динамической переменной являются те, что являются собственными значениями эрмитова оператора данной динамической переменной:

. (5.3)

Операторные уравнения являются математическими образами измерений. Операторы удобно рассматривать в качестве образов макроскопических приборов. Выражения для операторов основных динамических переменных. Оператор импульса и его rомпоненты (из формулы бегущей волны де Бройля). Операторы координат и оператор потенциальной энергии совпадают с самими этими переменными. Взаимосвязь операторов различных динамических переменных определяется тем, что они отображают макроскопическое устройство приборов. Операторы момента импульса одной частицы и его компонент имеют вид , оператор кинетической энергии единственной частицы равен , а для системы нескольких частиц представляет собою сумму вида . Радиус-вектор частицы , и его оператор представляет собой просто множитель перед волновой функцией, т.е. имеет вид: . Оператор потенциальной энергии это также просто множитель перед волновой функцией U(r), оператор полной энергии – гамильтониан складывается из операторов кинетической и потенциальной энергии: . (5.4) Принимается, что и операторы всех прочих динамических переменных построены из этих двух по формулам классической механики.

Причина классической схемы взаимосвязи кроется в том, что операторы являются образами макроскопически устроенных приборов, а конструкционные компоненты которых подчиняются законам классической (макроскопической ) физики.

Состояния и волновые функции, соответствующие определённым квантованным значениям физически наблюдаемой величины, - тем, которые непосредственно проявляются в измерениях, называются чистыми.

5.3. Постулат 3. Уравнения Шрёдингера (временнoе и стационарное)

Формулировка:

Волновые функции, описывающие возможные состояния изменяющейся во времени физической системы, являются решениями временного уравнения Шрёдингера :

. (5.5)

Для стационарной системы уравнение Шрёдингера принимает вид операторного уравнения на собственные значения гамильтониана:

(5.6)

Обратимся к стационарным системам. Введём гамильтониан, не зависящий от времени, и получится стационарное уравнение Шрёдингера. Выявим смысл комплексного сопряжения волновых функций как признак механической обратимости во времени решений уравнения Шрёдингера:

Результат (5.9) это стационарное уравнение Шрёдингера. Оно представляет собой операторное выражение закона сохранения энергии стационарной системы. Это чисто пространственная часть общего решения. Временная часть описывает периодический процесс.

Внимание! Операция комплексного сопряжения временной компоненты волновой функции состоит в замене знака перед аргументом - временем в показателе комплексной экспоненты. Эта простая алгебраическая операция совершенно идентична простой замене знака перед переменной времени. Получается, что при изменении отсчёта времени на обратное, не изменяются законы, которым починяется физическая система. Это важнейший результат, состоящий в том, что уравнение Шрёдингера описывает процессы, обратимые во времени.

5.4. Постулат 4. Суперпозиция состояний

Состояния чистые и смешанные. Математические и физические основания принципа суперпозиции

Формулировка 1 (скорее математическая):

Если две волновые функции _p и _q являются решениями операторного уравнения на собственные значения, то их линейная комбинация =c_p_p+ c_q_q также является его решением.

Истоки этой формулировки лежат в теории дифференциальных уравнений.

Формулировка 2 (скорее физическая):

Если система может находиться в состояниях с волновыми функциями _p и _q , то она может находиться и в состоянии с волновой функцией =c_p_p+ c_q_q.

Истоки этой формулировки происходят из убеждения, что до опыта нельзя предсказать, в каком состоянии находится система, а потому приходится допустить для неё сразу все возможности.

Речь о тех функциях, что совокупность которых образует спектр собственных функций эрмитова оператора (оператора динамической переменной). Эта ситуация может быть распространена на любое число собственных функций линейного самосопряжённого оператора:

Этот постулат называется принципом суперпозиции состояний и допускает обобщение на любое число собственных функций, образующих спектр эрмитова оператора. Функции _k отвечают так называемым чистым состояниям, а их суперпозиция  - смешанному состоянию.

5.5. Постулат 5. Средние значения динамических переменных. Математические ожидания для динамических характеристик состояний чистых и смешанных

Формулировка:

Среднее значение динамической переменной, полученное в результате серии ис-пытаний (измерений) совпадает с математическим ожиданием динамического оператора этой переменной, которое вычисляется по формуле:

; (5.11)

Для чистых состояний это уравнение является формальным следствием 2-го постулата, но для случая смешанных состояний эта формула постулируется и тем самым возводится в ранг физического закона.

5.6. Постулат 6. Принцип Паули

Формулировка:

Полная волновая функция, коллектива идентичных фермионов антисимметрична относительно перестановки любой пары частиц между их индивидуальными одночастичными состояниями.

Это свойство можно записать в виде

. (5.12)

5.7. О перестановочной симметрии коллектива частиц

Удобно ввести оператор перестановки , действие которого состоит в том, что он меняет местами идентичные частицы с номерами k и l между их одночастичными состояниями или что совершенно одно и то же – меняет состояния этих двух частиц между собой.

Если заранее оговорить, что всегда номера идентичных частиц в колективе определяются просто порядковым номером в цепочке-перечислении, то номер можно и не записывать в явной форме. В таком случае записывая в позиции частицы символ какой-то волновой функции, удобно считать её символом состояния, в которое частица попадает.

Действуя на волновую функцию, оператор перестановки исторгает из неё собственное значение, но при этом умудряется её самоё не изменять. Перед нею просто возникает некоторое число - собственное значение этого оператора. Если же оператор перестановки применить к волновой функции коллектива повторно, то обе переставляемые частицы возвращаются на исходные позиции – в исходные состояния, и волновая функция обязана обратиться вновь сама в себя. Система возвращается в исходную ситуацию, и поэтому собственное значение квадрата оператора перестановки равно единице. Получаем равенства:

Необходимая информация.

5.8. Фермионы

Поясним, что обязательный комплект переменных многофермионного коллектива включает не только пространственные переменные и время, но для каждой частицы вводится дополнительная степень свободы, называемая спиновой переменной, так что пространство переменных существенно расширяется.

Этот вопрос рассмотрим позднее, а сейчас его на время оставим...

Фермионами являются все частицы со спином, равным или кратным 1/2 (также возможно и 3/2, 5/2,...-это у некоторых ядер). Электроны и протоны суть фермионы. Их спин равен 1/2. Соответственно для электронного коллектива в молекуле должна быть построена электронная , а для коллектива идентичных протонов – уже своя - протонная волновая функция.

Уравнение Шрёдингера для простейших стационарных движений

6.1. Одномерный "потенциальный ящик"

и последовательный квантово-механический анализ свойств стационарной системы удобно проследить на примере простейшего поступательного движения, на ограниченном интервале. Волновые функции одной частицы называют орбиталями. Решение уравнения Шрёдингера превращаются в орбитали только после подчинения их условиям регулярности, предъявляемым к волновым функциям, а также после обязательной нормировки. Правило квантования энергии (энергетический спектр) вытекает из последовательного наложения граничных условий на решения уравнения Шрёдингера. Энергетический спектр не отличается от полученного для простой модели линейно ограниченной волны Де-Бройля. Энергетическую диаграмму и графики волновых