Геометрия вокруг нас
Вступление
«Понятия числа и фигуры взяты не откуда-нибудь, а только из действительного мира »
Ф.Энгельс
Каждый день на уроках математики мы узнаем о свойствах чисел и фигур, решаем задачи, а вернувшись домой, повторяем изученный материал, делаем домашнее задание. Большим помощником у нас является учебник. О многом можно узнать из него: как складывать десятичные и обыкновенные дроби, как решать уравнения, как строить графики и.т.д. Но про то, кем и когда были придуманы дроби, где впервые стали решать задачи с помощью уравнений, когда возникли отрицательные числа,- про все это в учебнике сказано очень мало. Не говорится в учебнике и о том, как применяют математику в различных играх, как ее используют для тайнописи, как применяют в строительстве
Хочется оглянуться вокруг и увидеть свойства геометрических фигур и тел, а также их широкое применение на практике.
-3-
Геометрия вокруг нас
Геометрия в переводе с греческого «гео»-земля, «метрео»-мерить. Как сказал великий ученый П.Рамус: «Геометрия-это наука хорошо измерять».
Многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Поверхности кирпича, спичечного коробка, куска мыла состоят из шести прямоугольных граней. Конечно, грани эти шероховаты, могут иметь выбоины или трещины, но с достаточной степенью точности можно вычислить их площади по формуле площади прямоугольника S=ab.
А опытный рабочий может так отшлифовать поверхность металлического бруска, что неровности не будут превышать нескольких тысячных долей миллиметра. Для таких поверхностей формула площади выполняется уже с большей точностью.
Чертежный угольник имеет форму прямоугольного треугольника с той лишь разницей, что геометрический треугольник не имеет толщины, а чертежный угольник ее имеет. Дощечки паркета, плитки, которыми покрывают полы в ванных комнатах и метро, сверху ограничены м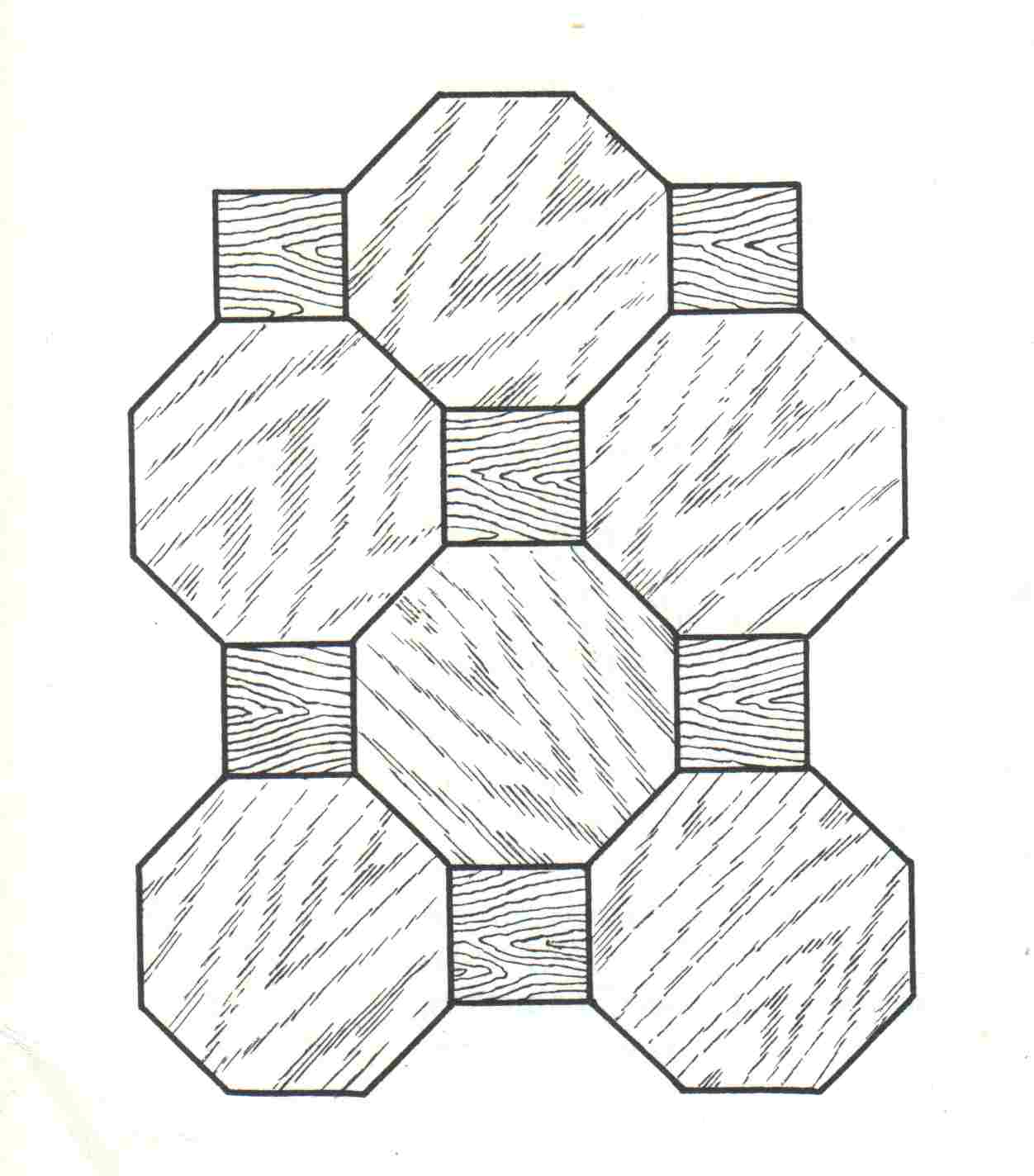 ногоугольниками.
ногоугольниками.
Комнаты, кирпичи, железобетонные блоки напоминают своей формой прямоугольный параллелепипед. Поэтому их объемы можно с хорошей точностью вычислить по формуле v=abc для объема прямоугольного параллелепипеда можно сложить новое тело той же формы, но большего размера. Например, из кирпичей или железобетонных блоков складывают стены зданий . Эти стены не падают. А если бы стены стали складываться из наклонных тел, то они завалились бы.
Е сли поставить круглый стакан на лист бумаги и обвести его дно карандашом, получится линия, похожая на окружность.
сли поставить круглый стакан на лист бумаги и обвести его дно карандашом, получится линия, похожая на окружность.
Но, посмотрев на эту линию через микроскоп, увидим
толстую неровную черту.
В геометрии изучают лишь окружности, не имеющие
толщины. Поэтому наша линия является только изобра-
жением той окружности, которую изучают в геометрии. Конечно,
чем тоньше карандаш, тем больше проведенная линия будет похожа на окружность.
-4-
М ногие вещи напоминают окружность- обруч, кольцо, дорожка вдоль арены цирка. Длину обруча или кольца можно вычислить по формуле l=2πr, где π=3,14… . орбиты планет, то есть линии, по которым они движутся вокруг Солнца,- это чуть-чуть сплюснутые окружности. Но для многих задач этим можно пренебречь и приближенно считать, что орбиты планет– окружности, центром которых является Солнце. Окружность является границей круга.
ногие вещи напоминают окружность- обруч, кольцо, дорожка вдоль арены цирка. Длину обруча или кольца можно вычислить по формуле l=2πr, где π=3,14… . орбиты планет, то есть линии, по которым они движутся вокруг Солнца,- это чуть-чуть сплюснутые окружности. Но для многих задач этим можно пренебречь и приближенно считать, что орбиты планет– окружности, центром которых является Солнце. Окружность является границей круга.
Арена цирка, дно стакана или тарелки имеют форму круга (по латыни «циркус» и означает слово круг).
Фигура, близкая к кругу, получится , если разрезать поперек арбуз.

Со времени изобретения гончарного круга люди научились делать круглую посуду- горшки, вазы, амфоры. 

К руглыми были и колонны, подпиравшие здания.
руглыми были и колонны, подпиравшие здания.
Среди круглых тел самым важным является шар. Расстояние всех точек поверхности шара от центра одно и то же. На геометрический шар похожи арбуз, глобус, футбольный мяч.


Поэтому, когда у футбольных болельщиков до матча спрашивают, с каким счетом он кончится, они часто отвечают: «Не знаем- мяч круглый».
Из всех тел заданного объема шар имеет наименьшую площадь поверхности. Из-за этого на космическом корабле, находящемся в состоянии
-5-
Невесомости, пролитая вода собирается в водяной шар. 
Форму шара имеют и громадные сгустки материи-звезды и, в частности, С олнце. Но из-за вращения вокруг оси они немного сплюснуты. Земля тоже имеет форму немного сплюснутого шара (расстояние от центра Земли до полюса равно 6357км, а до экватора- на 21км больше). Но часто говорят «земной шар», пренебрегая сжатием Земли.
олнце. Но из-за вращения вокруг оси они немного сплюснуты. Земля тоже имеет форму немного сплюснутого шара (расстояние от центра Земли до полюса равно 6357км, а до экватора- на 21км больше). Но часто говорят «земной шар», пренебрегая сжатием Земли.
Поверхность шара называют сферой. Если рассечь сферу плоскостью, в сечении получится окружность. Такие окружности имеют разные радиусы: чем дальше плоскость от центра сферы, тем меньше радиус сечения. Самые большие окружности получаются при сечении сферы плоскостями, проходящими через центр. Такими большими окружностями на земной поверхности являются экватор и меридианы. А параллели- это сечения земной поверхности плоскостями, параллельными плоскости экватора. 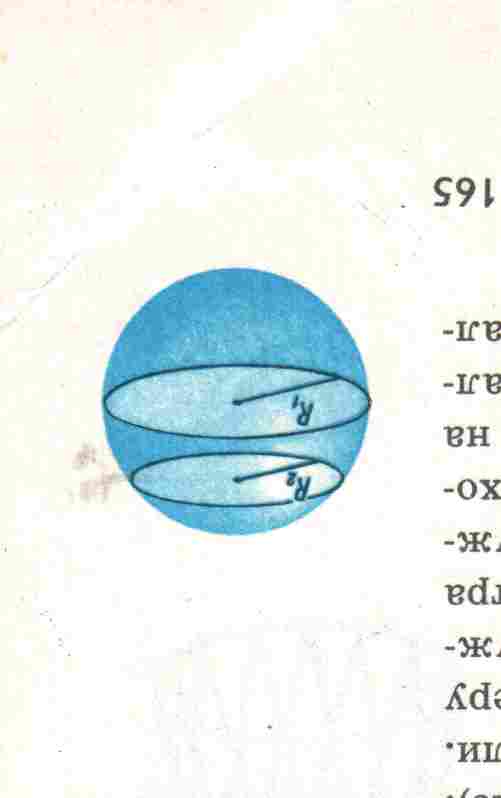
М
 ногие тела имеют форму геометрических фигур, названия которых вы еще не знаете. Шестигранный карандаш с боков ограничен шестью прямоугольниками, а снизу и сверху-правильными шестиугольниками. Такой же вид имеет плитка, которой покрывают пол. Только у карандаша высота больше стороны основания, а у плитки - меньше. Тела такой формы называют прямыми призмами. Призмы могут быть не только шестиугольными, но и треугольными, четырехугольными и т.д.
ногие тела имеют форму геометрических фигур, названия которых вы еще не знаете. Шестигранный карандаш с боков ограничен шестью прямоугольниками, а снизу и сверху-правильными шестиугольниками. Такой же вид имеет плитка, которой покрывают пол. Только у карандаша высота больше стороны основания, а у плитки - меньше. Тела такой формы называют прямыми призмами. Призмы могут быть не только шестиугольными, но и треугольными, четырехугольными и т.д.
Прямоугольный параллелепипед-это прямая четырехугольная призма, у которой основание-прямоугольник. Дом приблизительно имеет вид
-6-
прямоугольного параллелепипеда, покрытого сверху треугольной призмой (такую форму придают крыше, чтобы с нее стекало дождевая вода).
 Набатная башня Кремля составлено из нескольких параллелепипедов, усеченной четырехугольной пирамиды и восьмиугольной пирамиды.
Набатная башня Кремля составлено из нескольких параллелепипедов, усеченной четырехугольной пирамиды и восьмиугольной пирамиды.
геометрические фигуры различной формы можно узнать и в других замечательных сооружениях


-7-



Круглый карандаш, бревно, консервная банка имеют форму цилиндра. Цилиндрические предметы из металла или дерева вытачивают на токарном станке. На таком станке можно выточить и конус. Цветочный горшок имеет форму конуса с отрезанной нижней частью. Такую фигуру называют усеченным конусом.
Но не только такие простые фигуры встречаются в окружающем нас мире. Например, телевизионная башня, построенная замечательным русским инженером В.Г Шуховым состоит из частей, которые математики называют гиперболоидами вращения. 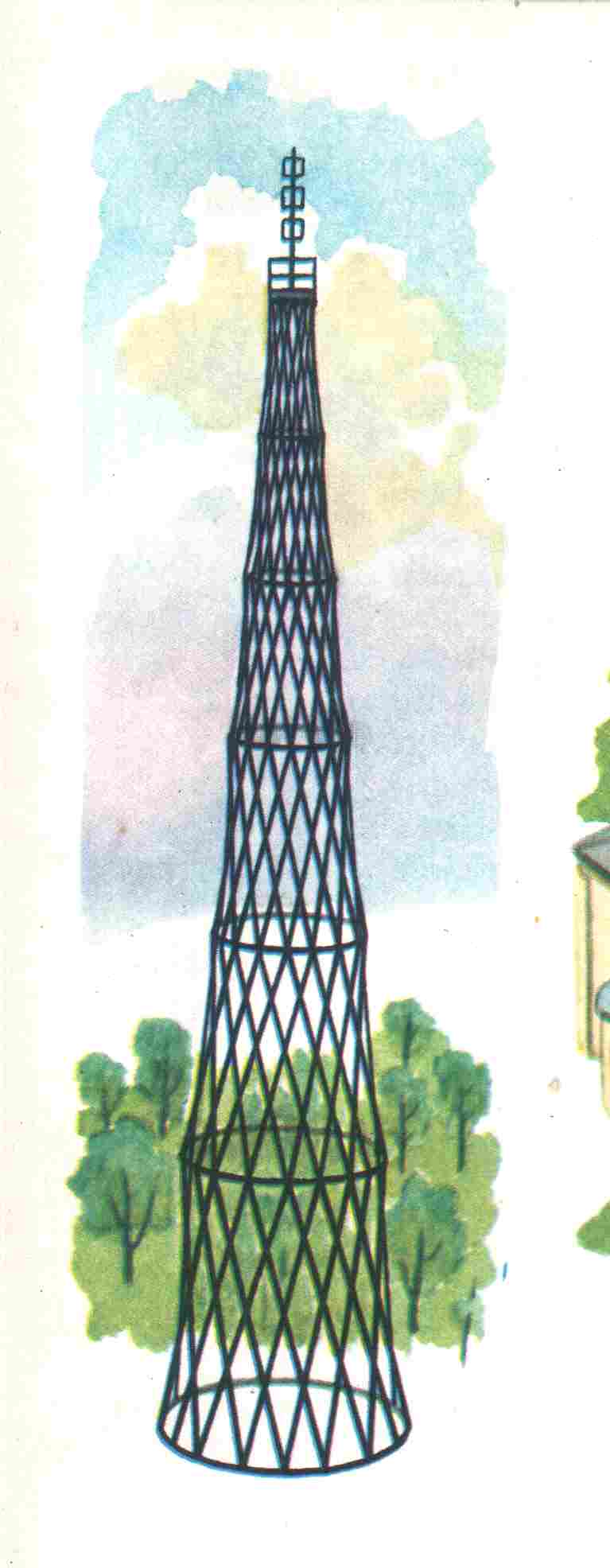 Хотя сами части кривые, они сложены из прямолинейных металлических балок. Этим Шухов облегчил возведение башни.
Хотя сами части кривые, они сложены из прямолинейных металлических балок. Этим Шухов облегчил возведение башни.
-8-
Заключение
Итак, мы рассмотрели различные примеры, показывающие, как широко применяется геометрия в окружающем нас мире. Геометрия необходима не только с научной точки зрения, но и с практической: в архитектуре, строительстве, физике, астрономии и т.д. сложную форму деталей имеют и детали машин – гайки, винты, зубчатые колеса и т.д. Но поверхности таких предметов можно изучать геометрическими методами. Поэтому геометрия необходима рабочим многих специальностей, имеющим дело с обработкой дерева и металла. Я уверена, что данный материал заинтересует других ребят и покажет всю красоту и значимость такой прекрасной науки – геометрии.
Его можно рассматривать как на уроках геометрии, так и на факультативах и других внеклассных мероприятиях. Как сказал великий русский поэт А.С. Пушкин: «Вдохновение нужно в геометрии, как в поэзии.»
-9-
Список литературы:
1 «За страницами учебника математики» пособие для учащихся 5-6 классов средней школы. И.Я. Депман, Н.Я Виленкин. Москва «Просвещение», 1989 г.
2 И.И. Зубарева, А.Г.Мордкович «Математика 5 класс» учебник для общеобразовательных учреждений. Москва «Мнемозина», 2005.
3 Л.С. Атанасян «Геометрия 7-9» учебник для общеобразовательных учреждений. Москва, «Просвещение»,2004 г.
-10-
Муниципальное общеобразовательное учреждение
Черемушкинская средняя общеобразовательная школа № 1 г.Саяногорск
Секция математики
Геометрия вокруг нас
Автор
Соколович катя- ученица 5 класса
Руководитель
Жукова Галина Анатольевна
2007 г.
Г. Саяногорск
П.Черемушки
1 вступление__________________________3
2 основная часть:
Геометрия вокруг нас________________4
3 заключение__________________________9
4 список литературы__________________10

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ