Конспект урока для 11 класса «Производная и ее геометрический смысл»
Урок разноуровневого обобщающего
повторения в 11 классе на тему
«Производная и ее геометрический смысл».
Урок подготовила и провела:
учитель математики
Тарада Елена Борисовна
Цели:
обобщить и систематизировать теоретические знания по темам: «Вычисление производных» и « Геометрический смысл производной»; рассмотреть методы решения заданий ЕГЭ, связанных с понятием производной базового и повышенного уровней сложности; организовать работу учащихся по указанным темам согласно уровню их сформированных знаний.
Оборудование:
ПК учителя, мультимедийный проектор.
Индивидуальные карточки для проведения разноуровневой самостоятельной работы.
Презентация, содержащая материал для повторения и закрепления теоретических знаний, для фронтального опроса по теории.
ХОД УРОКА
I этап урока – организационный (2 минуты).
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится у них на парте.
II этап урока – повторение теоретического материала по теме «Производная и ее геометрический смысл» (12 минут).
Учитель задает учащимся вопрос: «Что называется производной функции?»
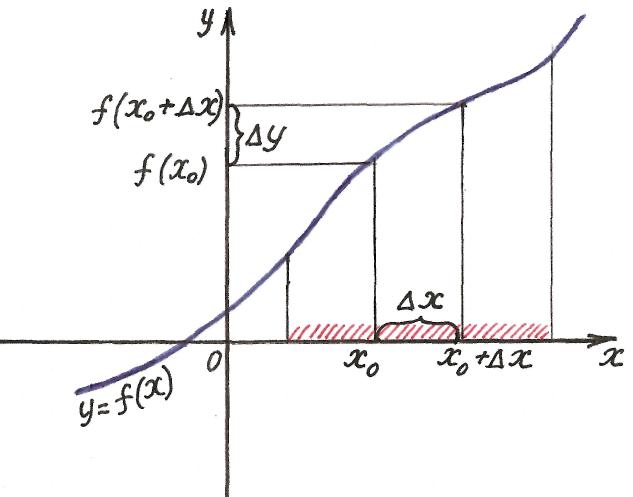 На экране – слайд № 1.
На экране – слайд № 1.
Ответ: Пусть функция y = f(x) определена в некотором интервале, содержащем внутри себя точку x0. Дадим аргументу приращение ![]() такое, чтобы не выйти из этого интервала. Если существует предел отношения приращения функции
такое, чтобы не выйти из этого интервала. Если существует предел отношения приращения функции ![]() (при переходе от точки x0 к точке
(при переходе от точки x0 к точке ![]() ) к приращению аргумента при
) к приращению аргумента при ![]() , то указанный предел называют производной функции
, то указанный предел называют производной функции ![]() в точке x0.
в точке x0.
Учитель: «А теперь вспомните формулы производных элементарных функций. Чему равна:
- производная постоянной функции ![]() ;
;
- производная линейной функции ![]() ;
;
- производная степенной функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ;
;
- производная функции ![]() ?»
?»
На экране – слайд № 2.
C′ = 0 (kx + m)′ = k ![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
Учитель: «Сформулируйте правила вычисления производных. Чему равна:
- производная суммы функций;
- производная произведения функций;
- производная частного функций;
- производная функции ![]() ?».
?».
Слайд № 3.
(u + v)′ = u′ + v′
(uv)′ = u′v +u v′
(ku)′ = ku′
![]() =
= ![]()
![]() = k f ′(kx+m)
= k f ′(kx+m)
Соответствующие формулы на слайдах № 2, 3 появляются по мере ответов учащихся.
Учитель: «Как называется прямая, проходящая через две точки графика функции?»
Ответ учащихся: секущая.
Учитель: «Какая прямая называется касательной к кривой L в точке M?».
Слайд № 4
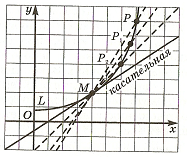
Учащиеся должны ответить, что касательная есть предельное положение секущей.
Учитель: «Как найти угловой коэффициент касательной? Угловой коэффициент секущей?»
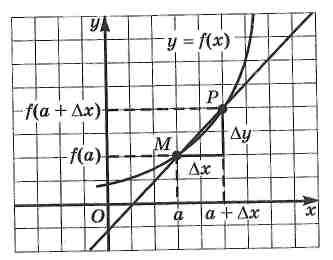 Слайд № 5.
Слайд № 5.
Ответ: ![]() - угловой коэффициент секущей; угловой коэффициент касательной
- угловой коэффициент секущей; угловой коэффициент касательной ![]()
Учитель: «В чем состоит геометрический смысл производной?»
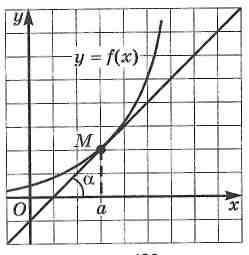 Слайд № 6
Слайд № 6
Ответ: Если к графику функции ![]() в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как
в точке с абсциссой x = a можно провести касательную, непараллельную оси y, то f ′(a) выражает угловой коэффициент касательной, а так как ![]() , то f ′(a)=
, то f ′(a)= ![]() .
.
Учитель: «Что можно сказать о знаке производной функции в точке x0, если касательная, проведенная к графику функции в точке с абсциссой x0, образует с положительным направлением оси абсцисс острый угол?»
Слайд № 7

Ответ: Производная в точке x0 положительна.
Учитель: «Что можно сказать о знаке производной функции в точке x0, если касательная, проведенная к графику функции в точке с абсциссой x0, образует с положительным направлением оси абсцисс тупой угол?»
Слайд № 8

Учащиеся отвечают, что в этом случае производная в точке x0 отрицательна.
Учитель: «Что можно сказать о значении производной в том случае, когда касательная к графику функции в точке с абсциссой x0 параллельна оси абсцисс?»
Слайд № 9

Ответ: Производная этой функции в точке x0 равна нулю.
Кроме того, учитель просит записать на доске уравнение касательной к графику функции y = f (x) в точке с абсциссой x0: y = f (x0) + f ′(x0)(x – x0)
III этап урока – устная работа по теме урока (10 минут).
Учитель: «Итак, ребята, сейчас вы должны применить сведения, которые повторили на уроке, на практике»
Слайд № 10
Найдите производную функции:
Ответы:
y = tg(5x)
y′ = − 5
f ′(x) =
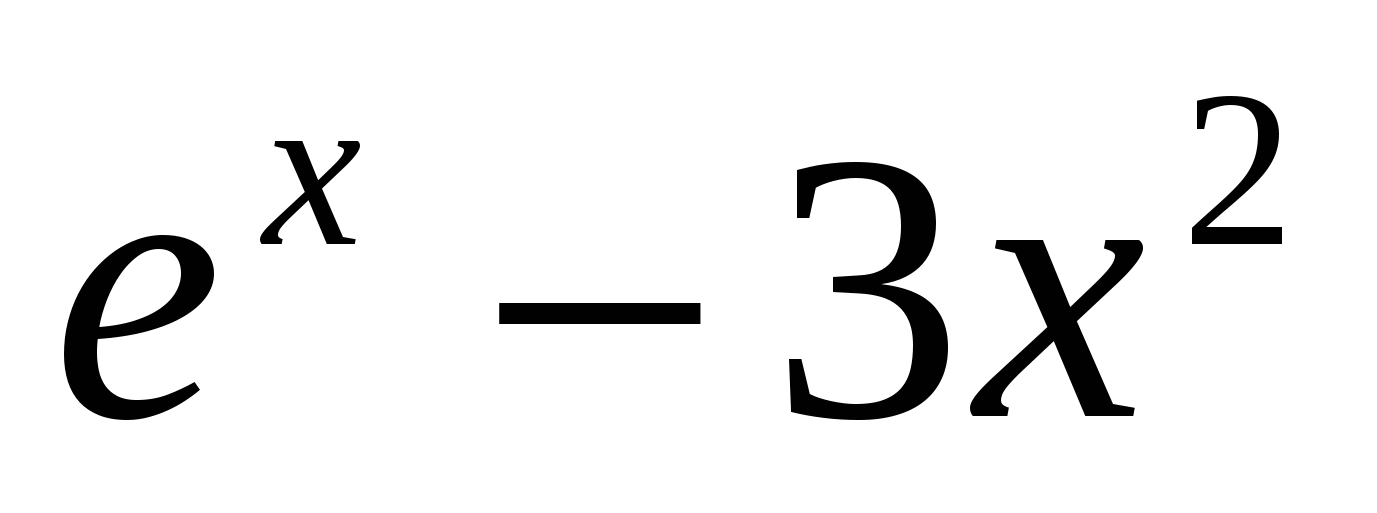
f ′(x) =
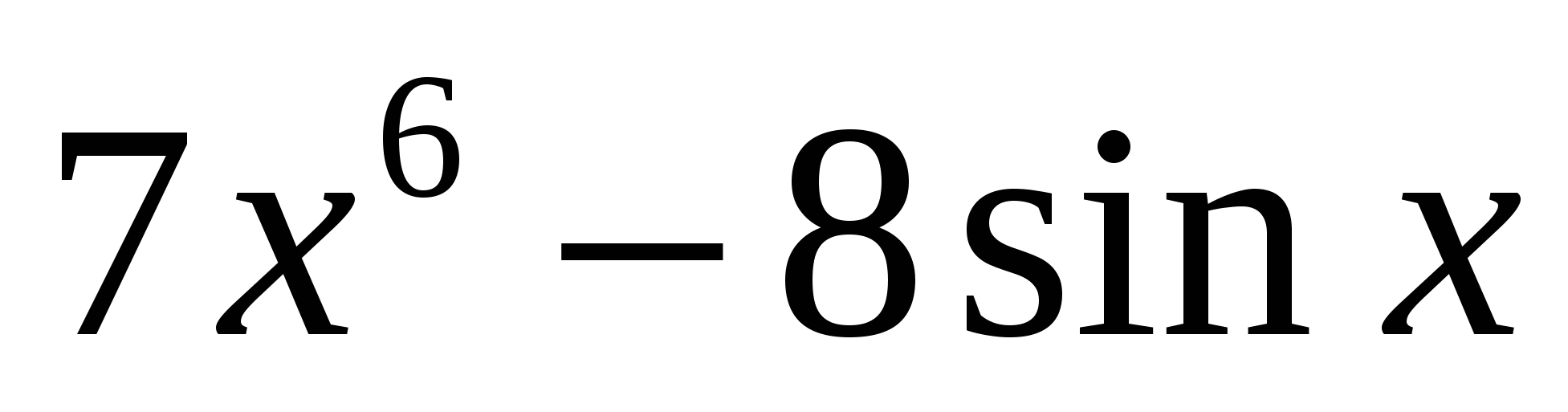
y′ =
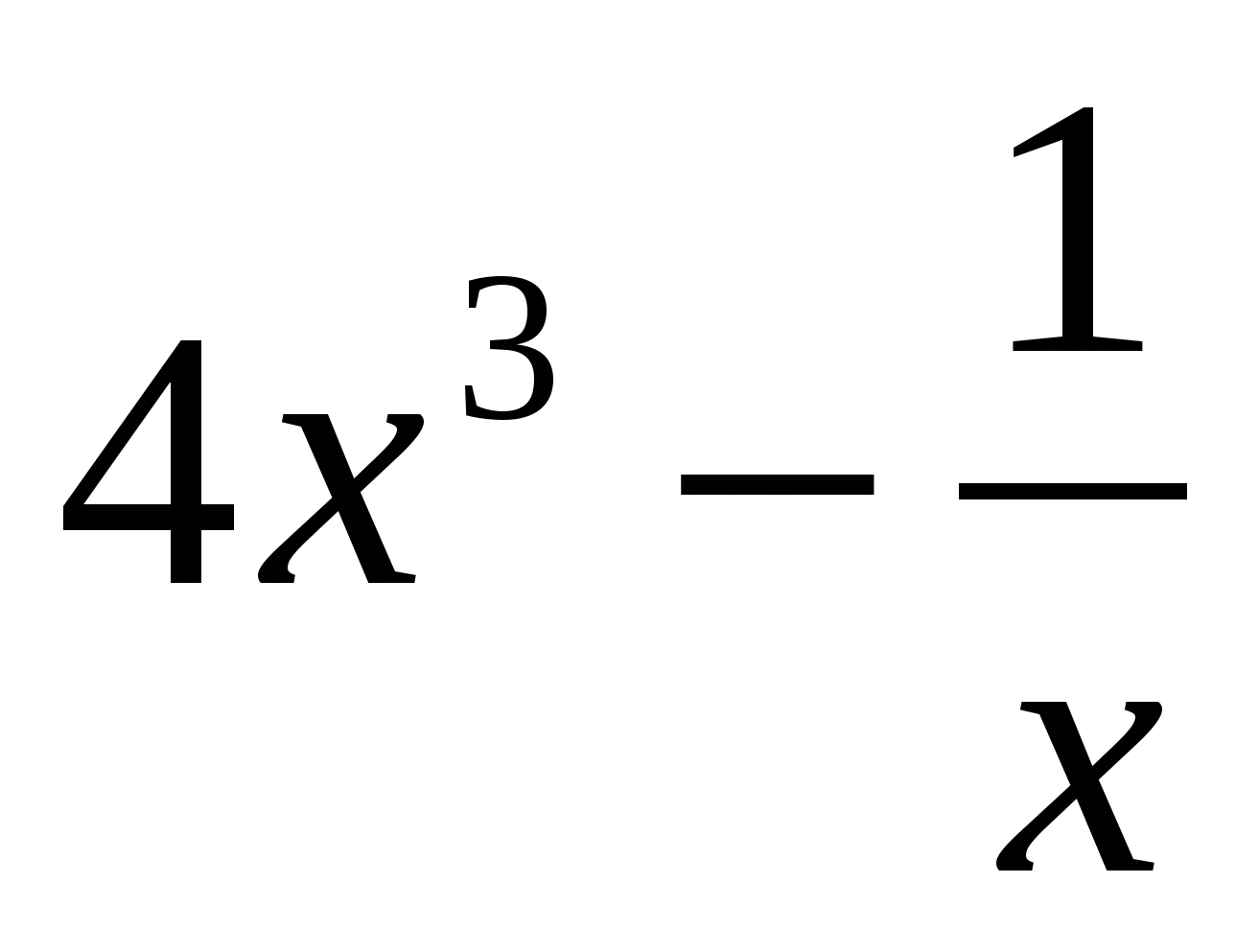
y′ =
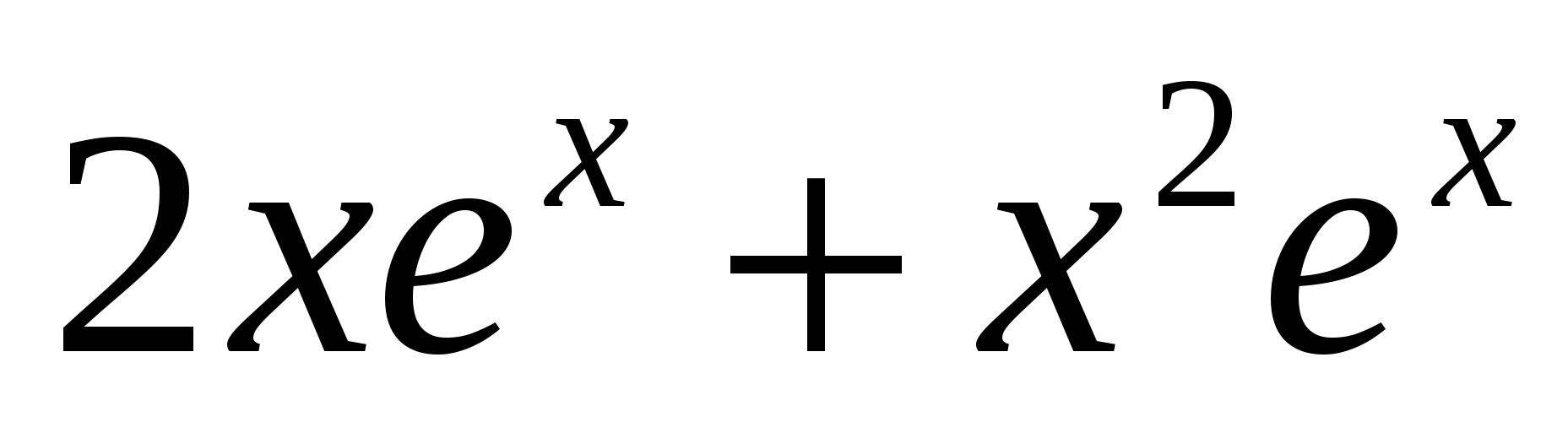
y′ =
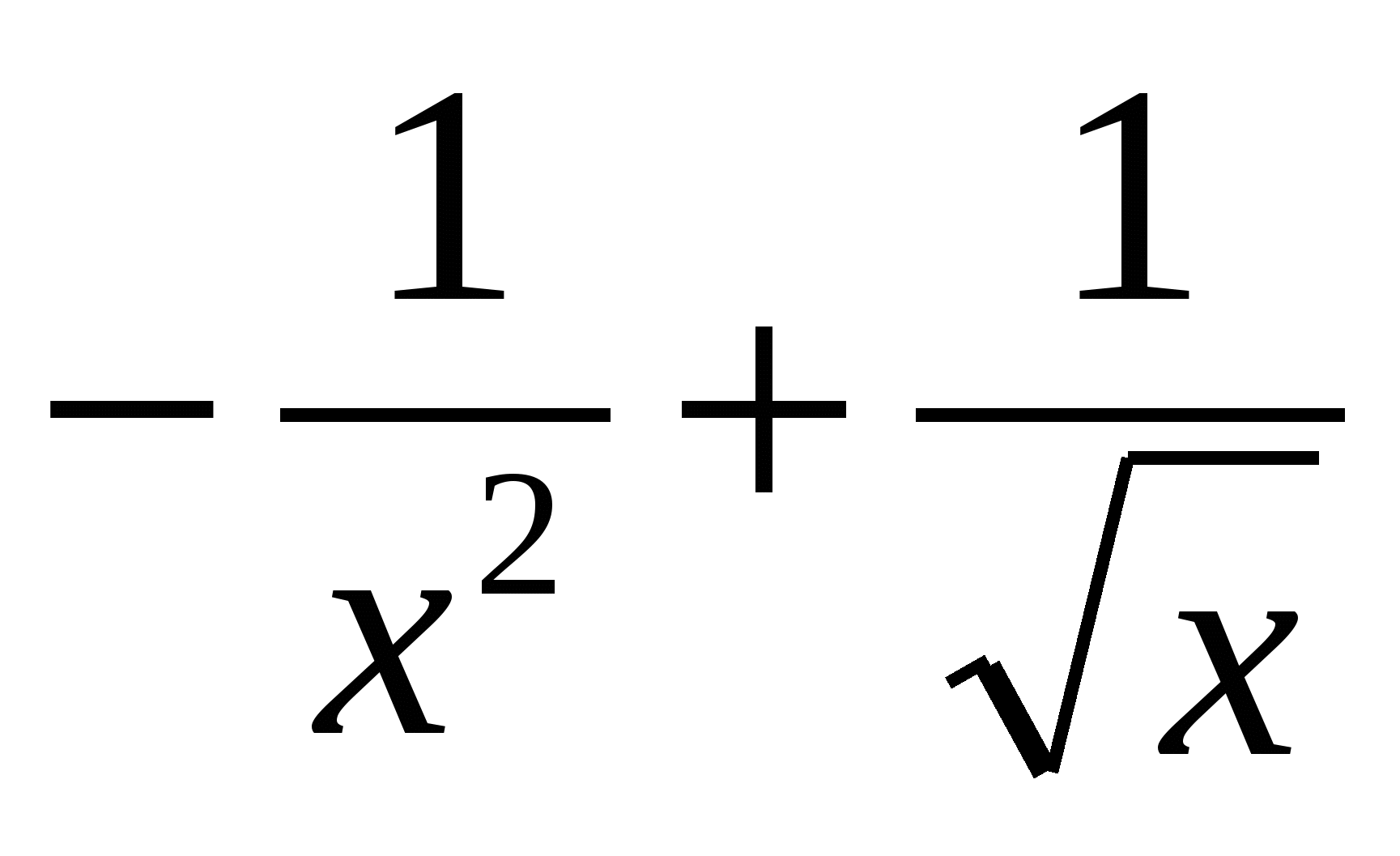
y′(x) =
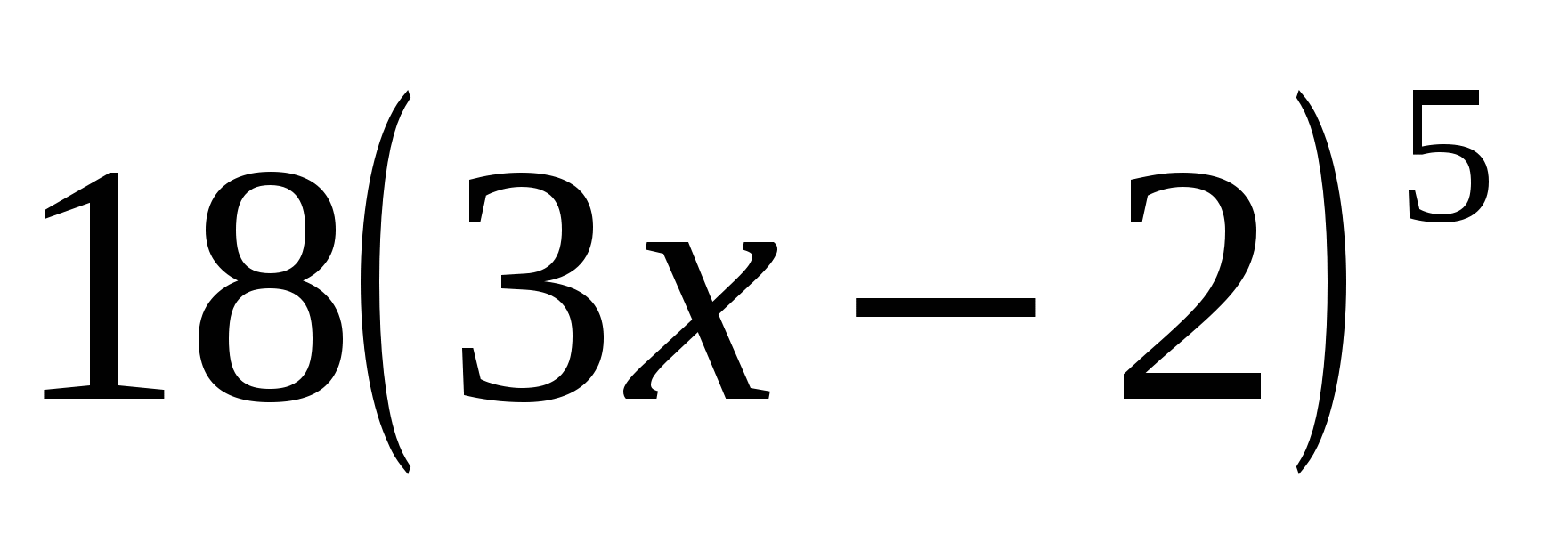
y′ =
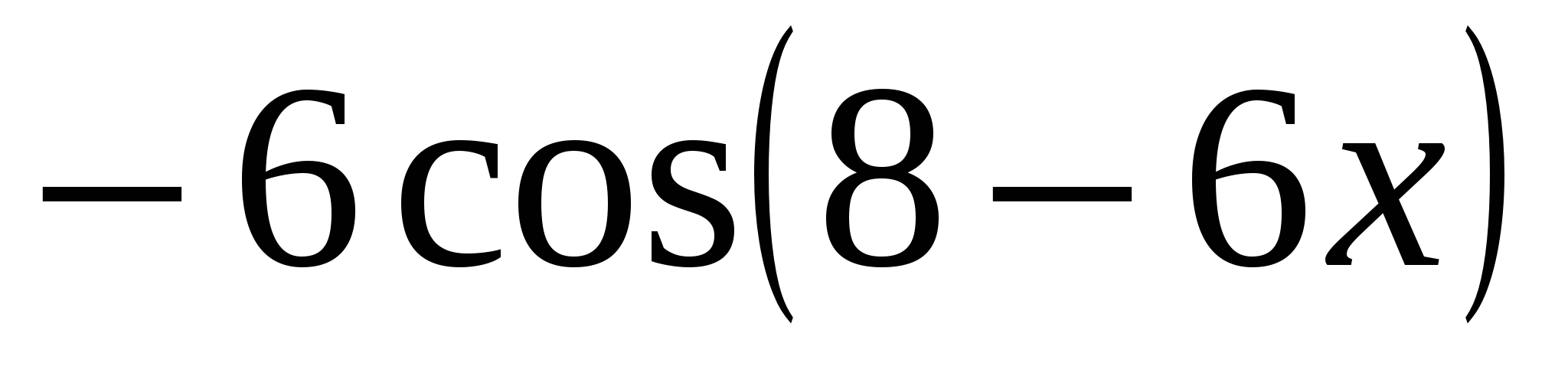
y ′=
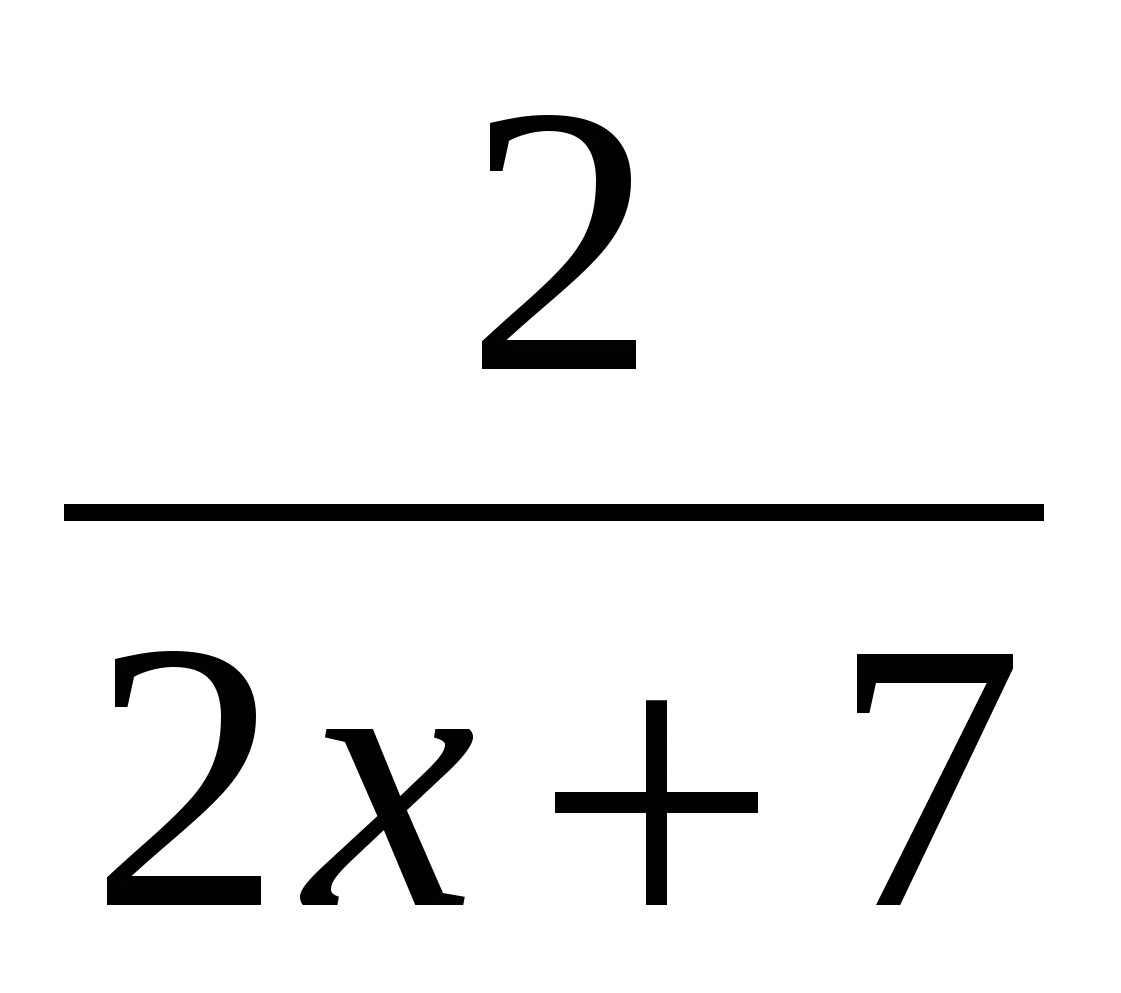
y′ =
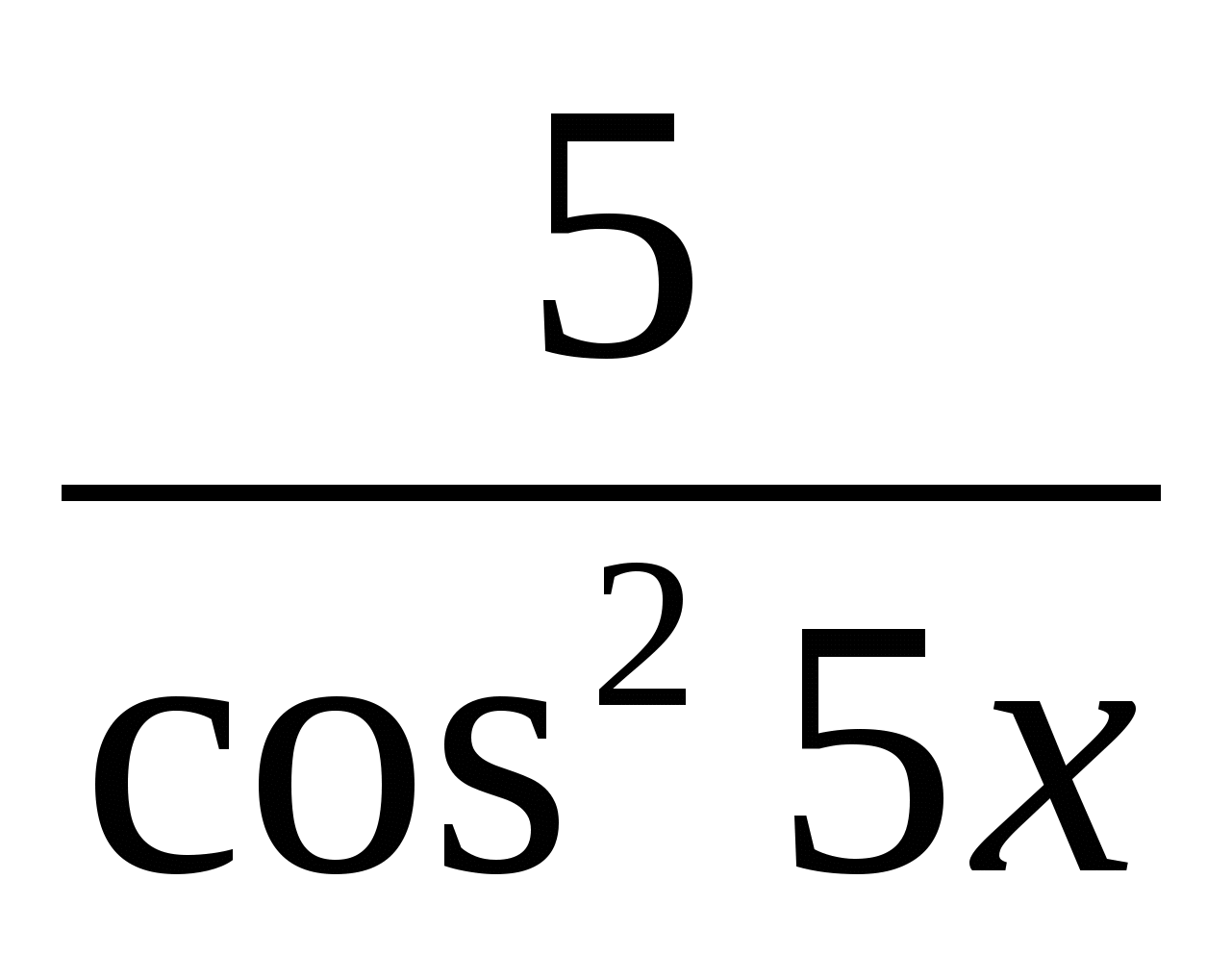
По мере ответов учащихся ответы появляются на слайде.
Слайд № 11
На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
1)

2)

3)

Ответы:
№ 1
№ 2
№ 3
1
− 0,5
0
 Слайды № 12 – 14
Слайды № 12 – 14
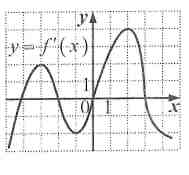
На рисунке изображен график производной функции у = f '(х). Найдите угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой х0 = 2.

Найдите значение производной
 .
.
Функция у = f(x) определена на промежутке (−4; 4). На рисунке изображён график её производной. Определите по графику у = f '(x) градусную меру угла наклона касательной к положительному направлению оси Ох в точке с абсциссой x0 = − 2 .
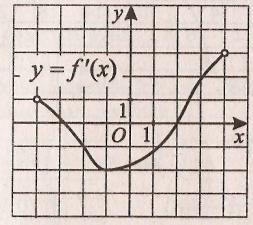
Ответы:
№ 1
№ 2
№ 3
4
− 1
135

1) Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции
. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции ![]() имеет наибольший угловой коэффициент.
имеет наибольший угловой коэффициент.

2) Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции.
. На рисунке изображен график производной этой функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.

3)Функция ![]() определена на промежутке
определена на промежутке ![]() . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной ![]() , определите количество касательных к графику функции
, определите количество касательных к графику функции ![]() , которые составляют угол
, которые составляют угол ![]() с положительным направлением оси Ox.
с положительным направлением оси Ox.
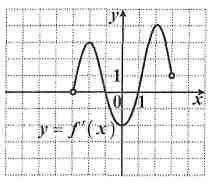
4) Функция у = f (x) определена на промежутке (− 3; 3). Используя изображенный на рисунке график производной y=f'(x), определите количество касательных к графику функции
у = f (х), параллельных оси Ох.
Ответы:
№ 1
№ 2
№ 3
№ 4
− 2
5
3
2
IV этап урока – разноуровневая самостоятельная работа (16 минут).
Учитель выдает задания для самостоятельной работы, сообщая учащимся, что на её выполнение отводится 16 минут.
Для учащихся 1-й группы учителем составлены карточки уровня А в двух вариантах. Учащиеся 1-й группы – это как правило, учащиеся со слабой математической подготовкой, они будут выполнять задания под контролем учителя. Работа для них содержит простейшие задания на вычисление производных элементарных функций, аналогичные тем, которые разбирались на уроке. Все задания в варианте базового уровня сложности. Для учащихся 2-й группы (средний уровень подготовки) учителем составлены карточки в четырех вариантах (уровень В). Учащимся 3-й группы учитель выдает карточки с задачами повышенного уровня сложности в двух вариантах (уровень С).
Вместе с заданиями учащиеся получают бланки для выполнения заданий.
Уровень А
Вариант 1
Вычислите значение производной функции
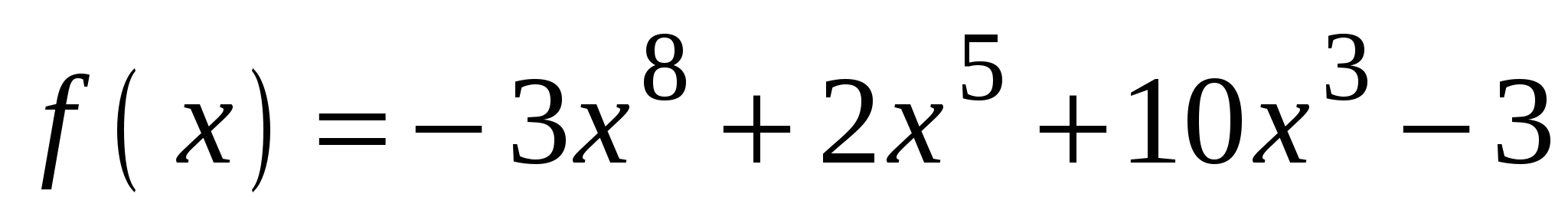 в точке
в точке 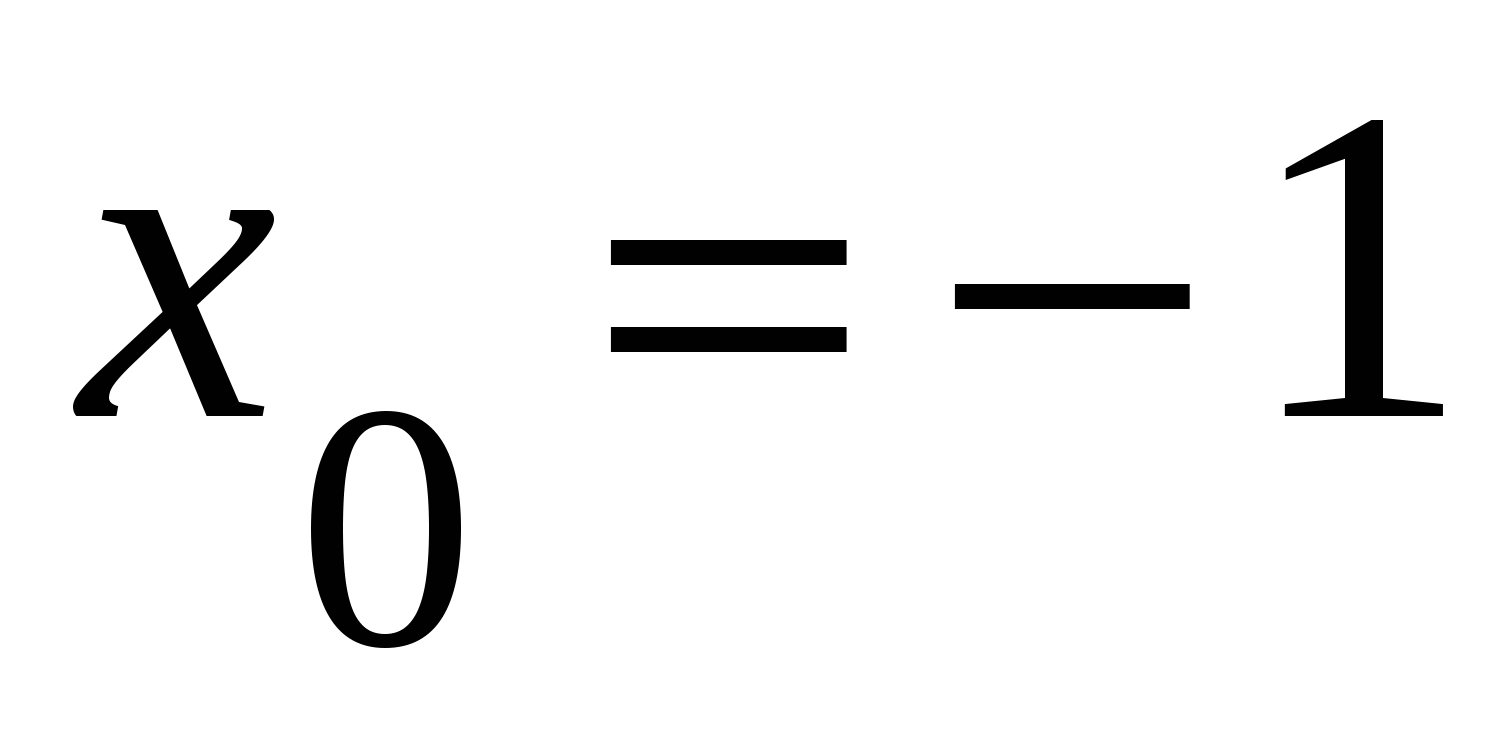 .
.
1)
16
2)
64
3)
– 16
4)
– 64
Найдите производную функции
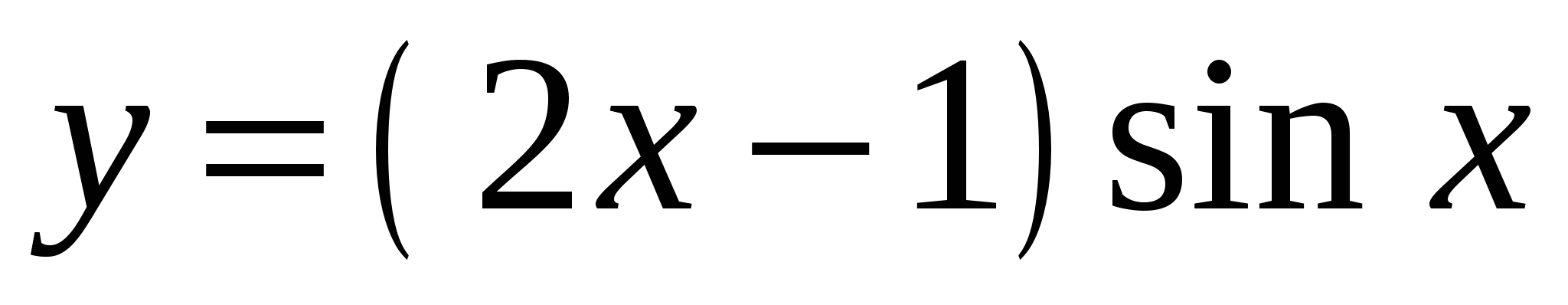 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
Найдите угловой коэффициент касательной, проведенной к графику функции
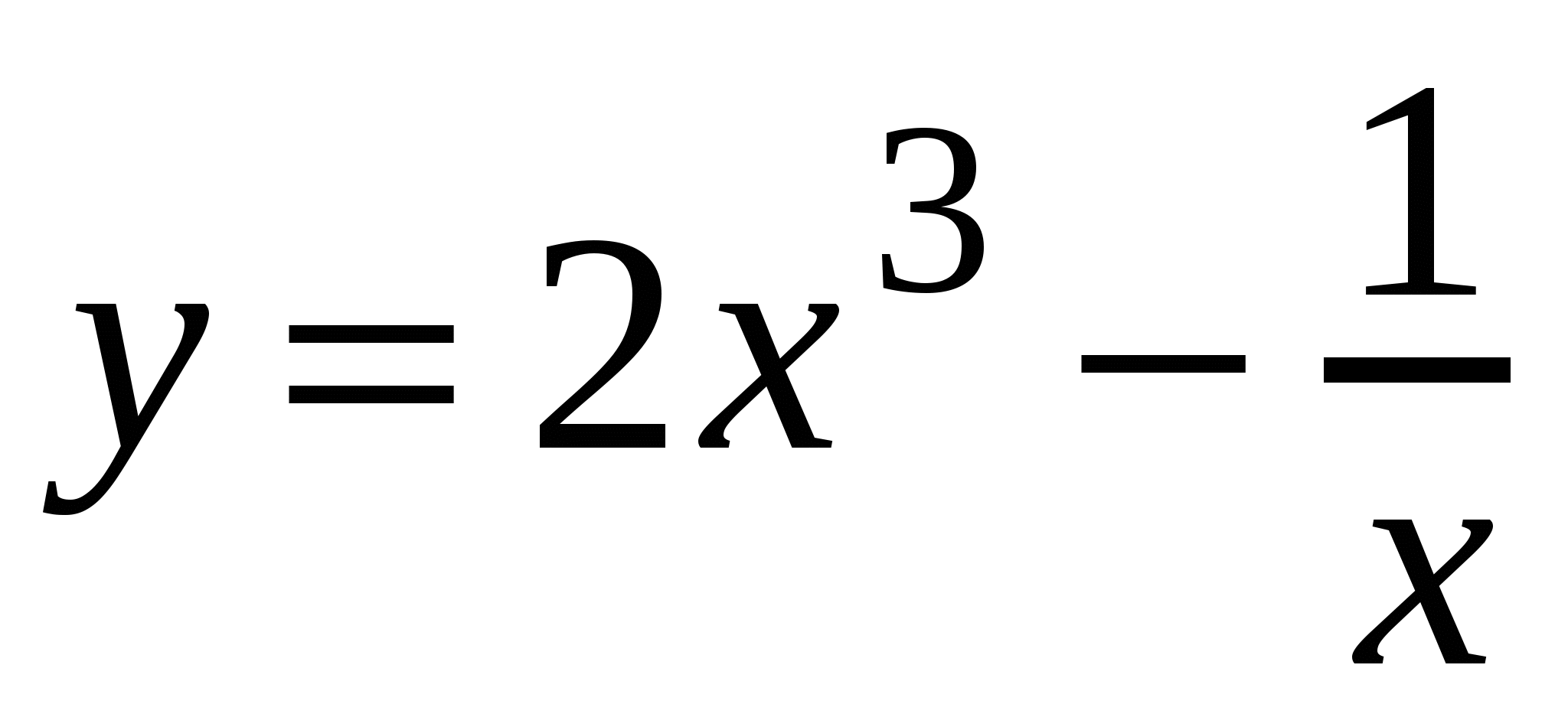 в его точке с абсциссой
в его точке с абсциссой 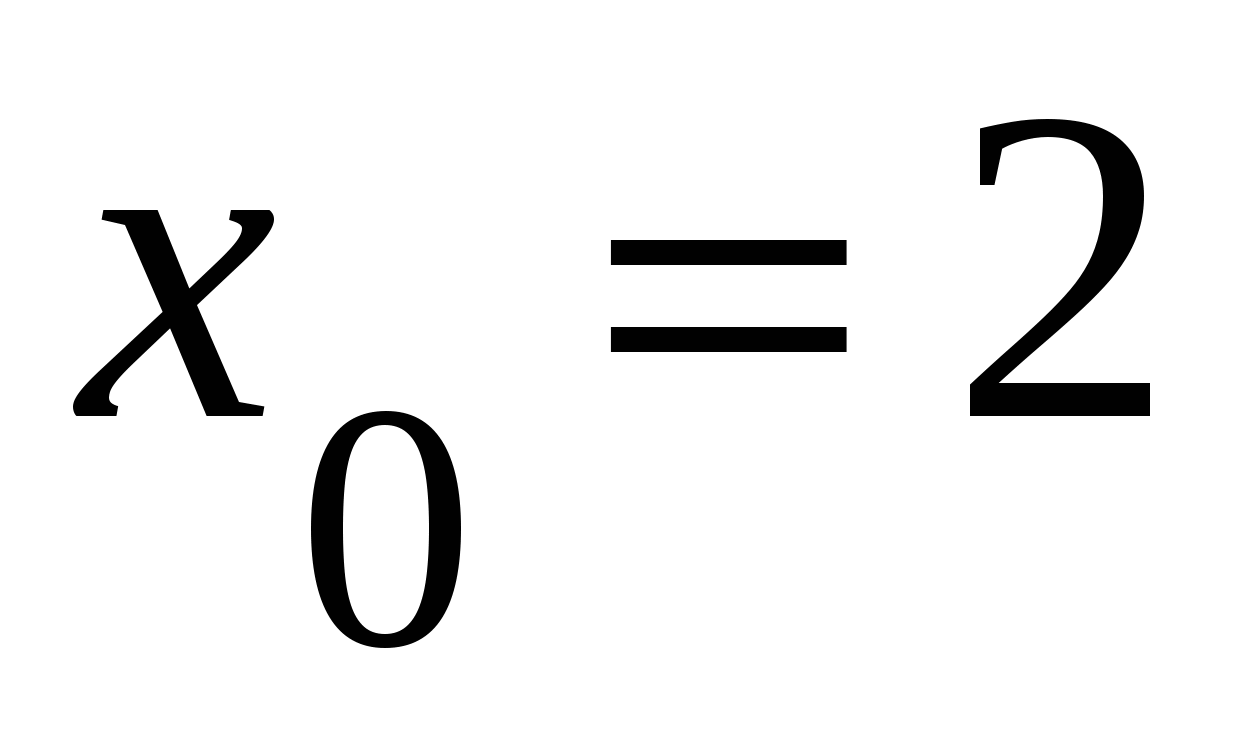 .
.
1)
22
2)
23,75
3)
24,25
4)
24
На графике функции
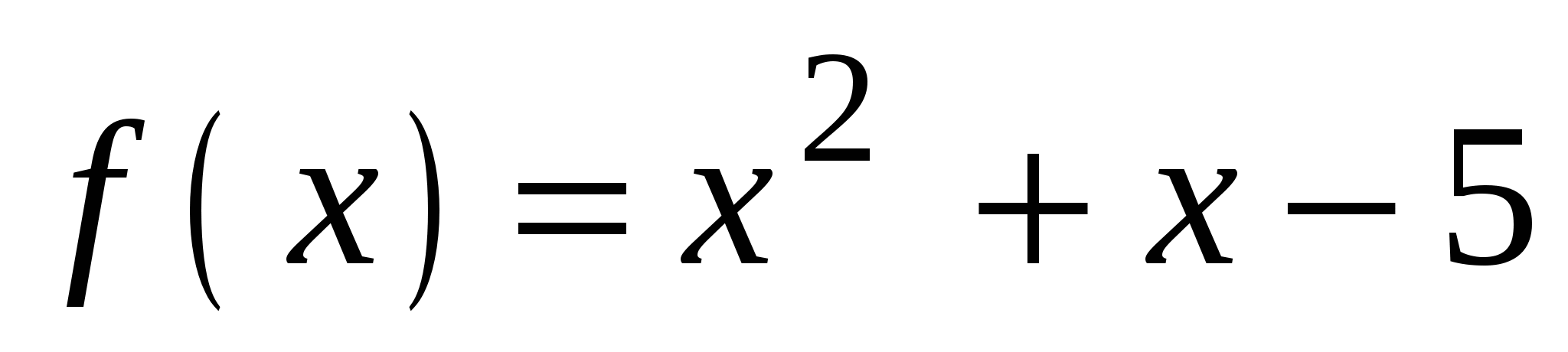 взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.
взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.
1)
1
2)
3
3)
![]()
4)
2
5. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.

Вариант 2
Найдите значение производной функции

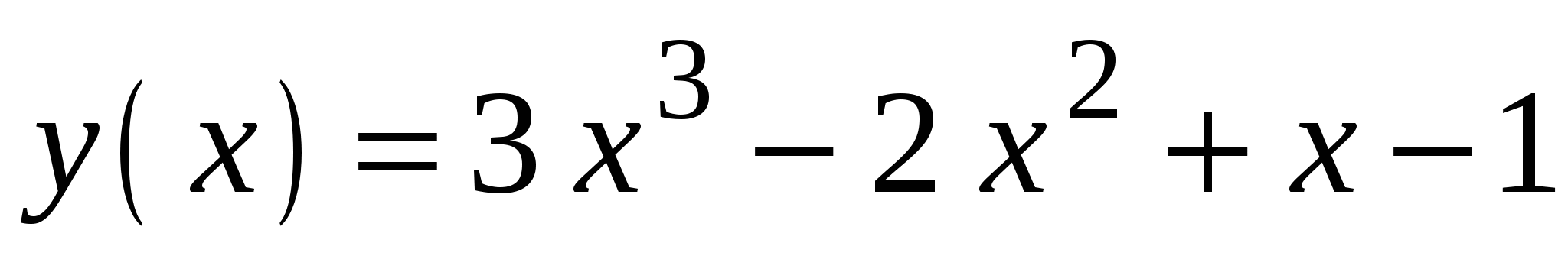 в точке с абсциссой
в точке с абсциссой 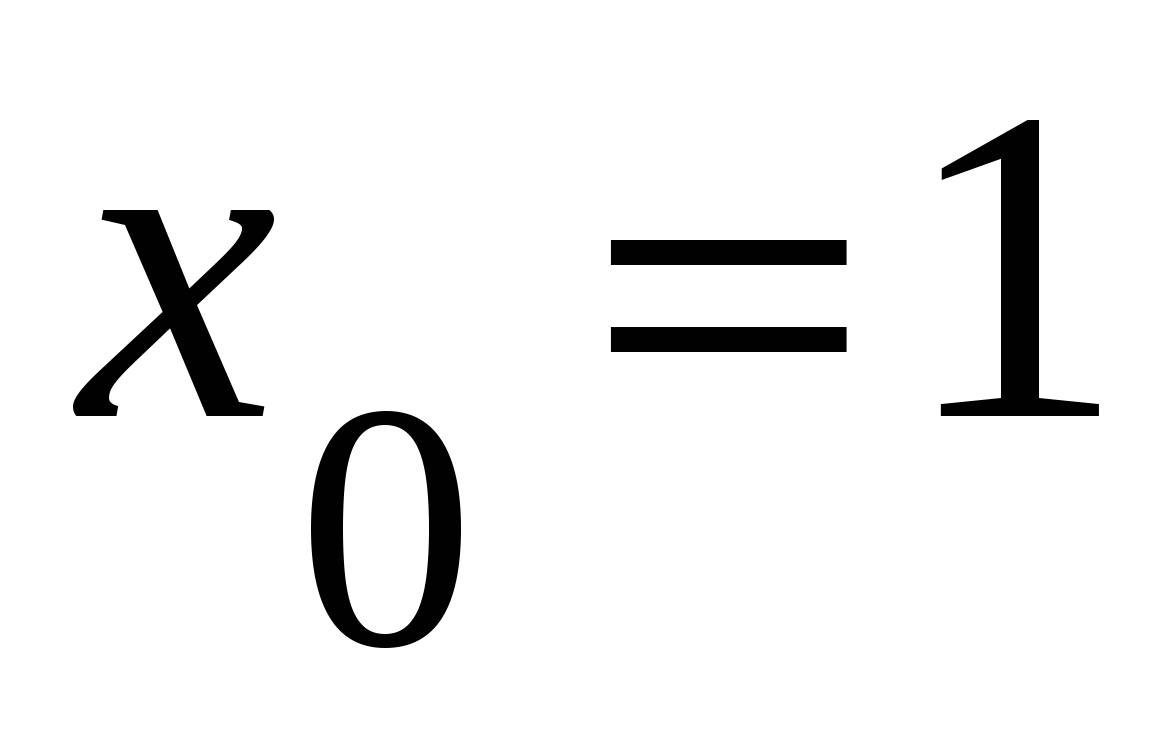 .
.
1)
9
2)
5
3)
4
4)
6
Найдите производную функции
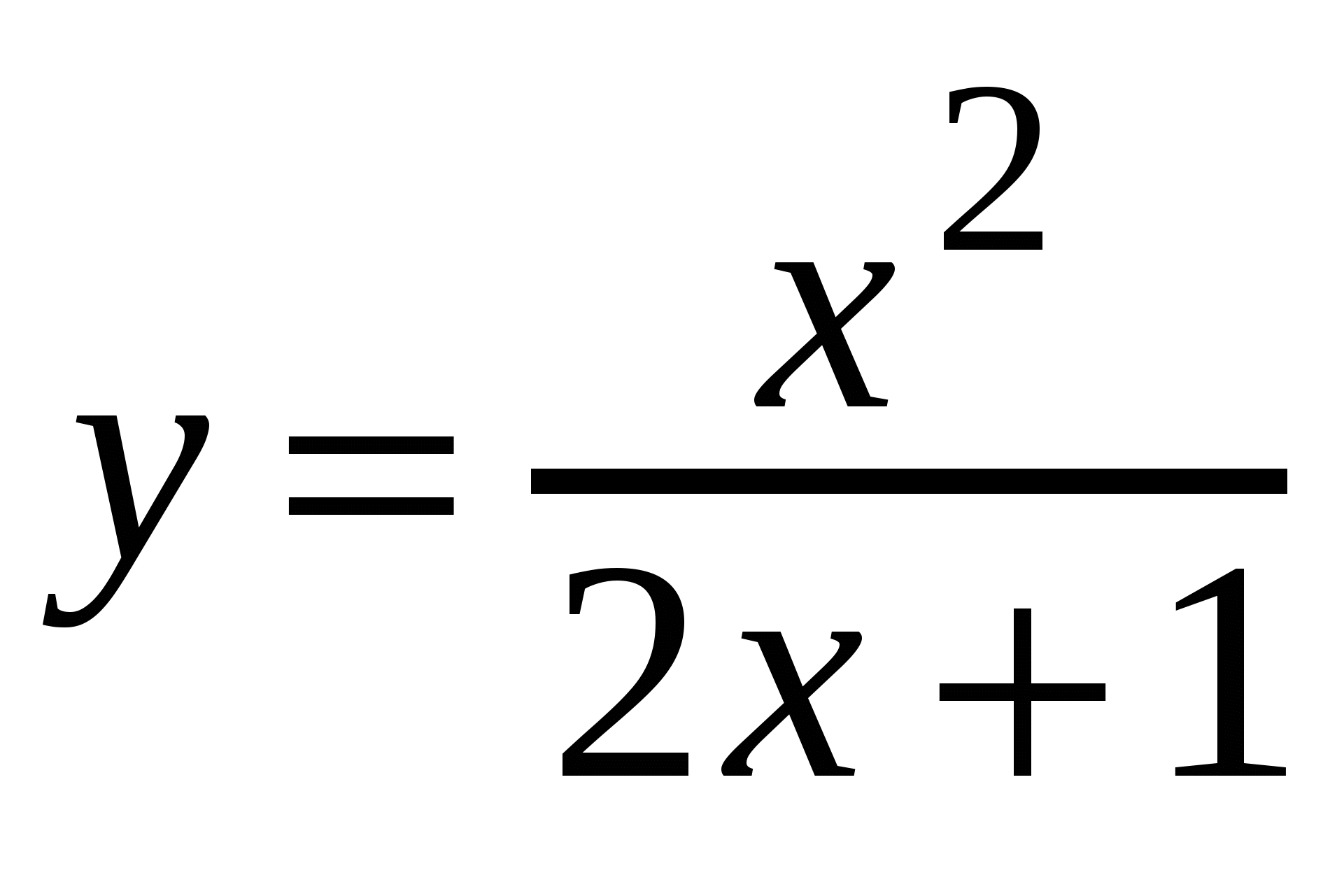 .
.
1)
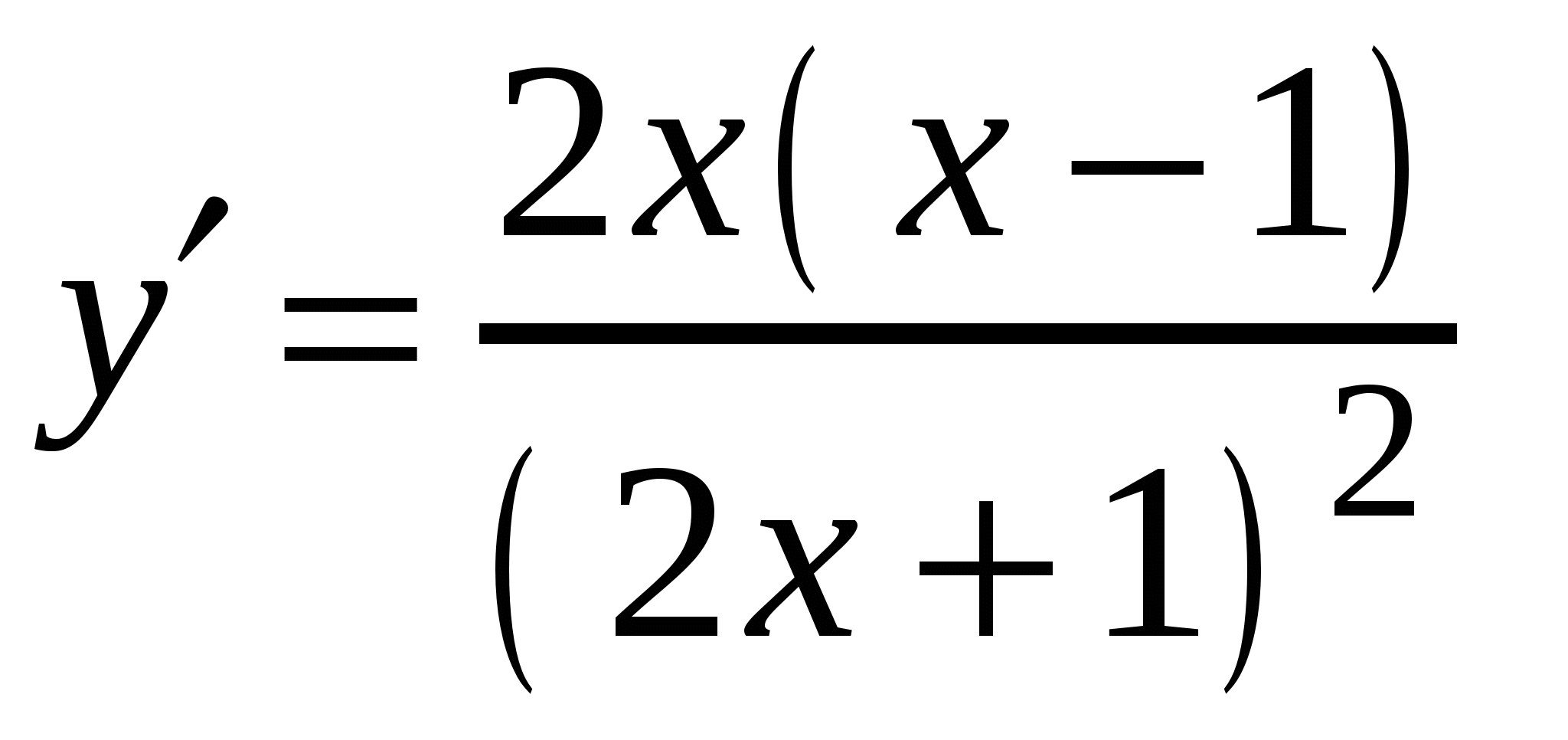
3)
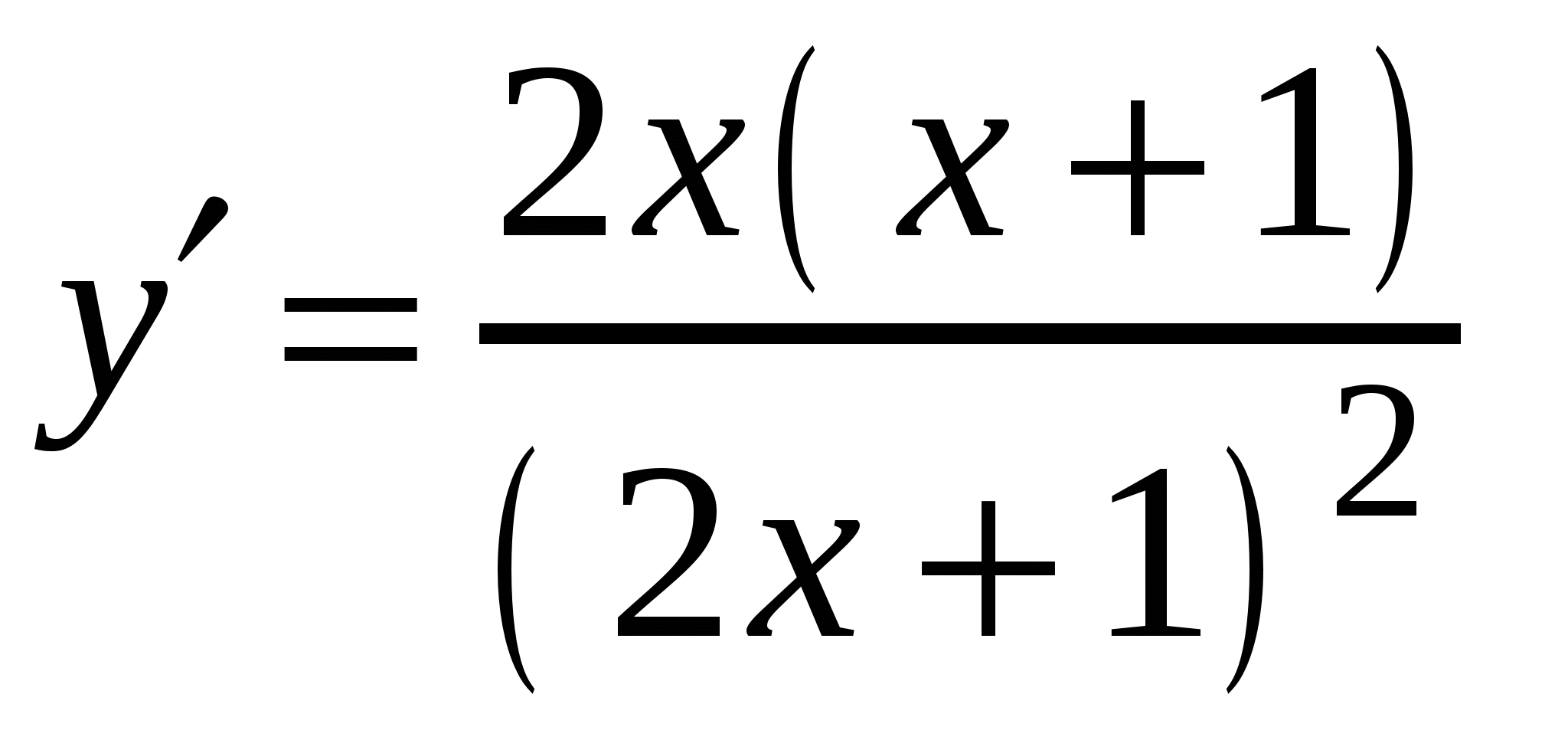
2)
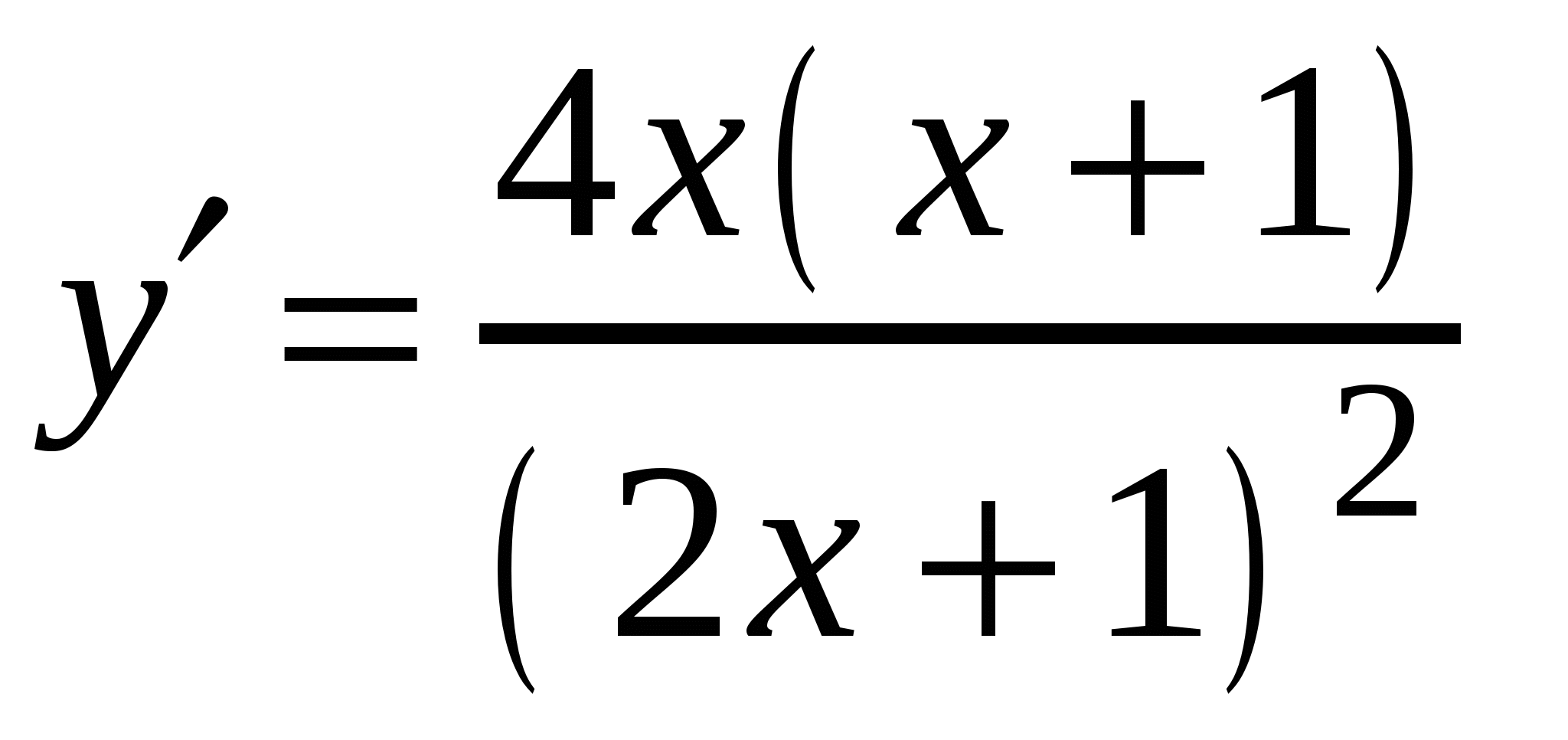
4)
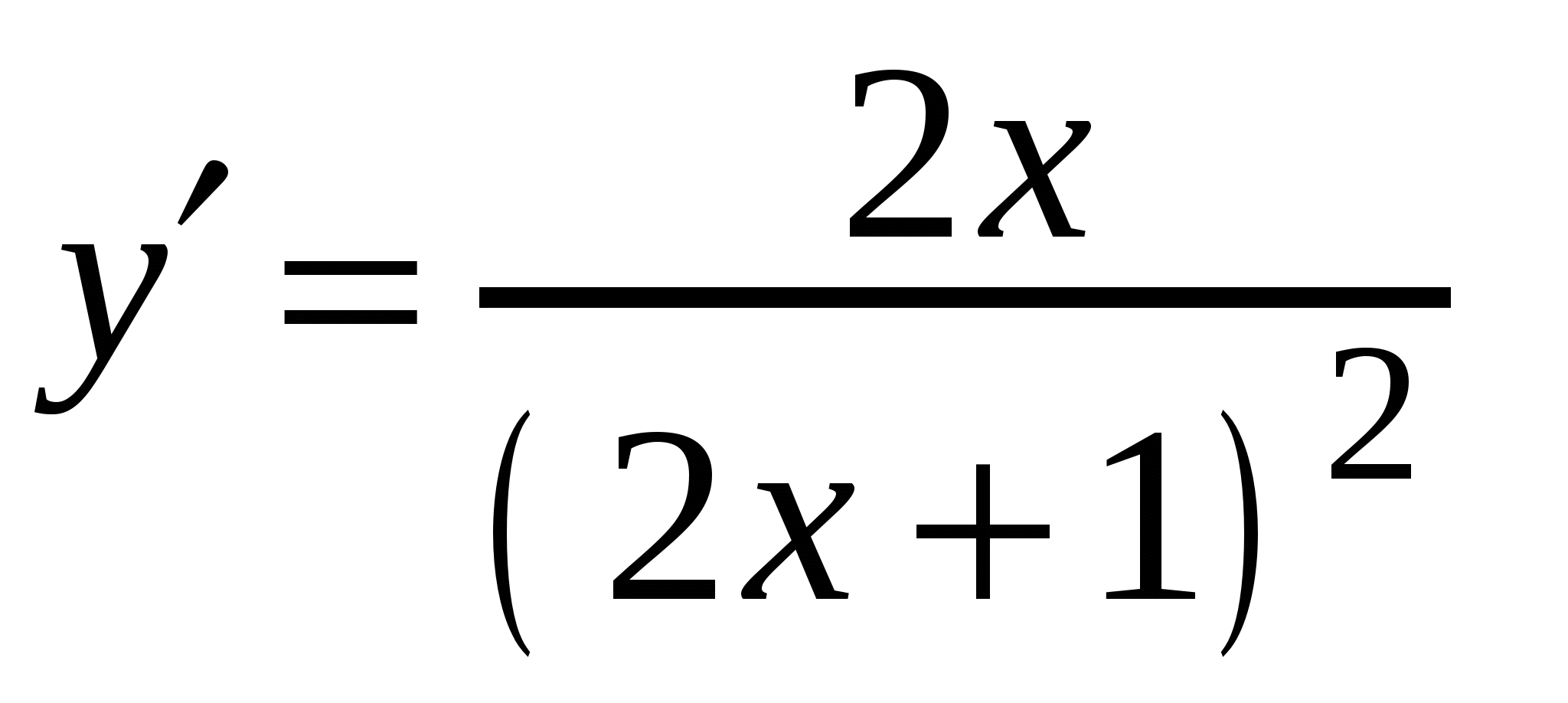
Найдите угловой коэффициент касательной, проведенной к графику функции
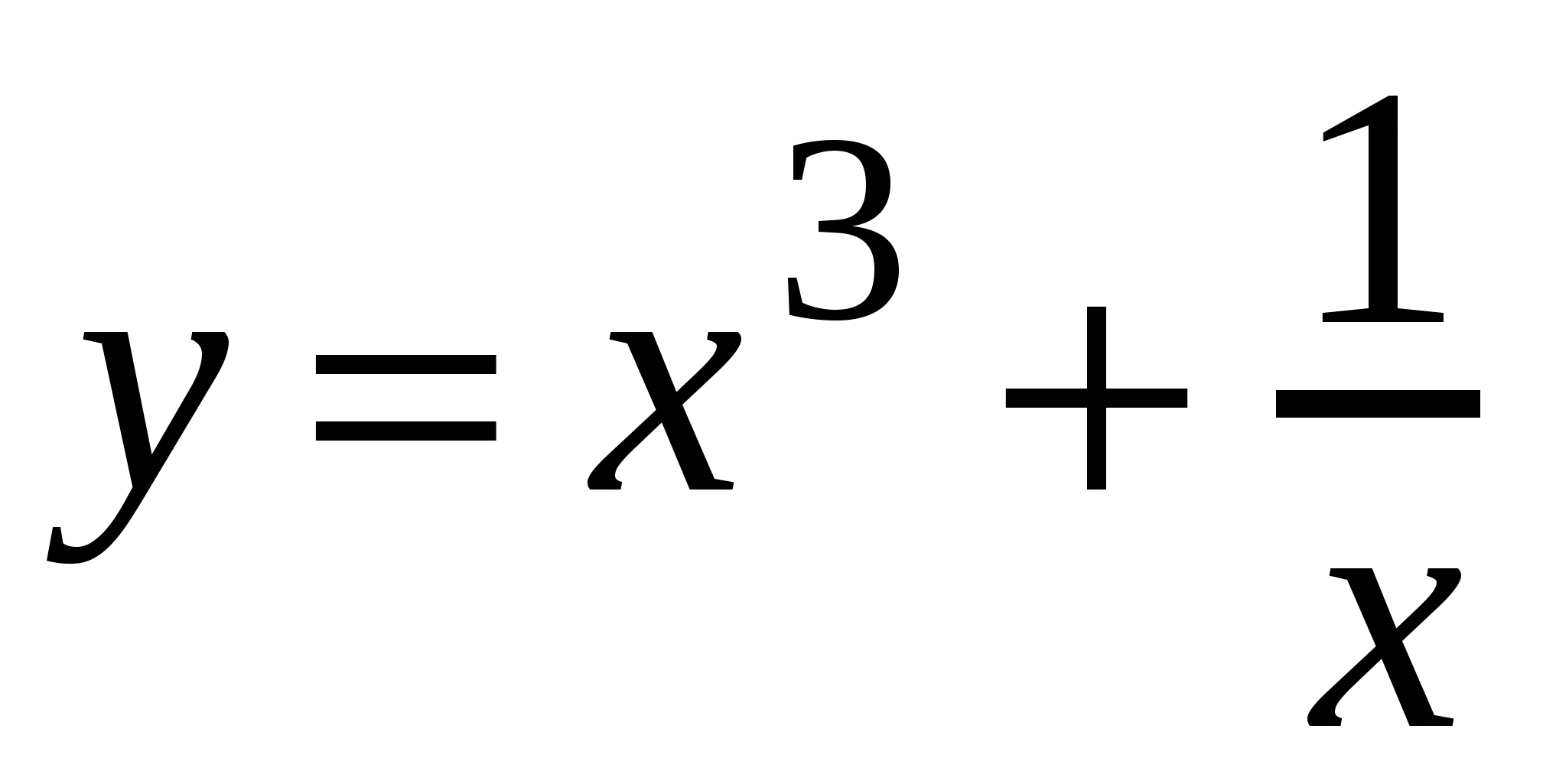 в его точке с абсциссой
в его точке с абсциссой 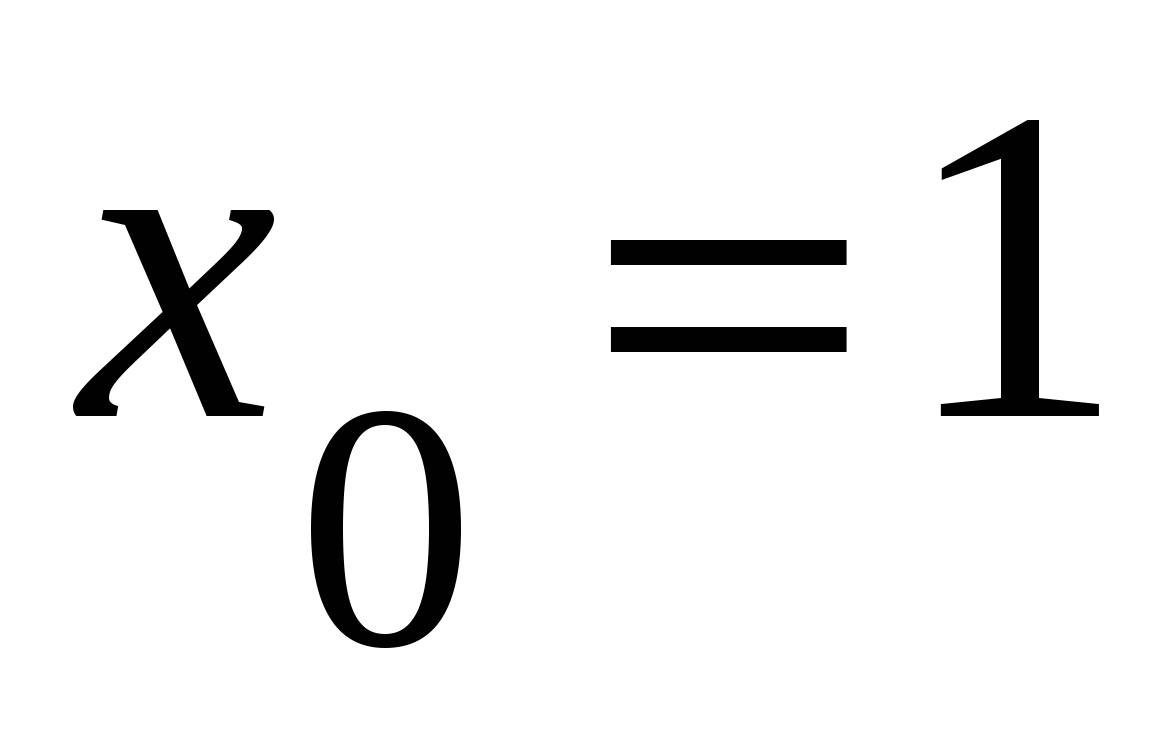 .
.
1)
2
2)
3
3)
4
4)
1
Определите абсциссу точки, в которой касательная к графику функции
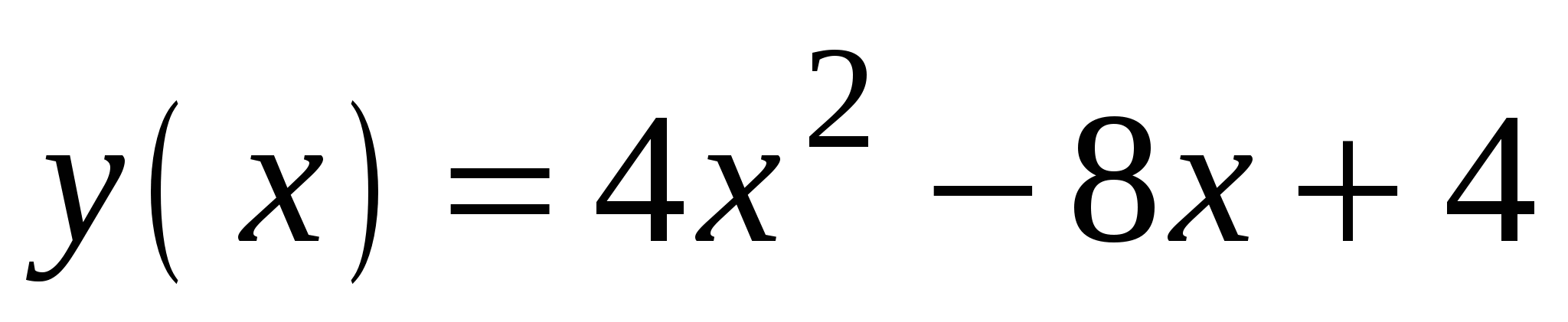 параллельна оси абсцисс.
параллельна оси абсцисс.
1)
– 8
2)
1
3)
0
4)
4
5. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.

Ответы:
Номер задания
1
2
3
4
5
Вариант 1
2
1
3
4
1,5
Вариант 2
4
3
1
2
−1
Уровень В
Вариант 1
Найдите производную функции
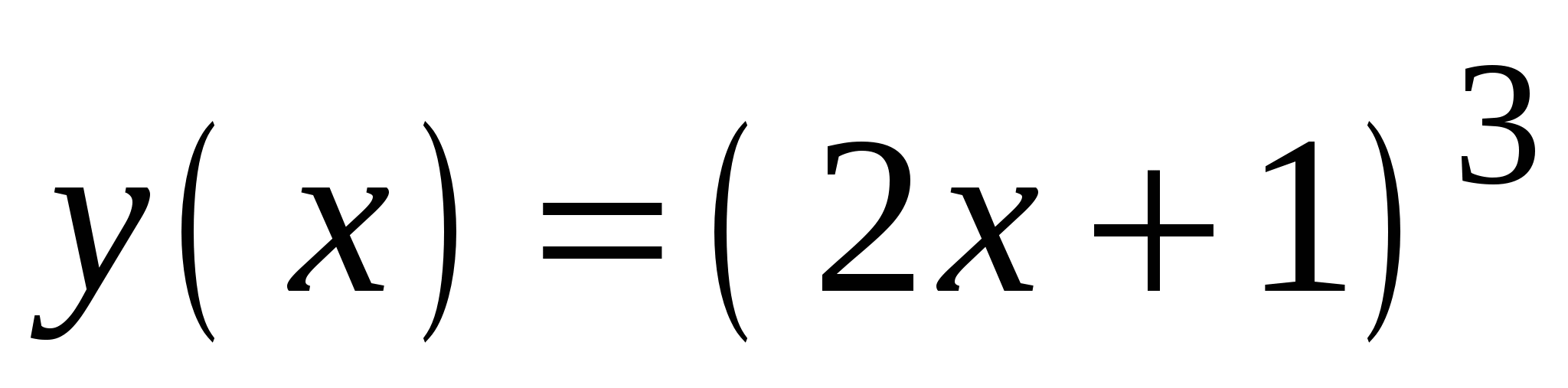 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
Найдите производную функции
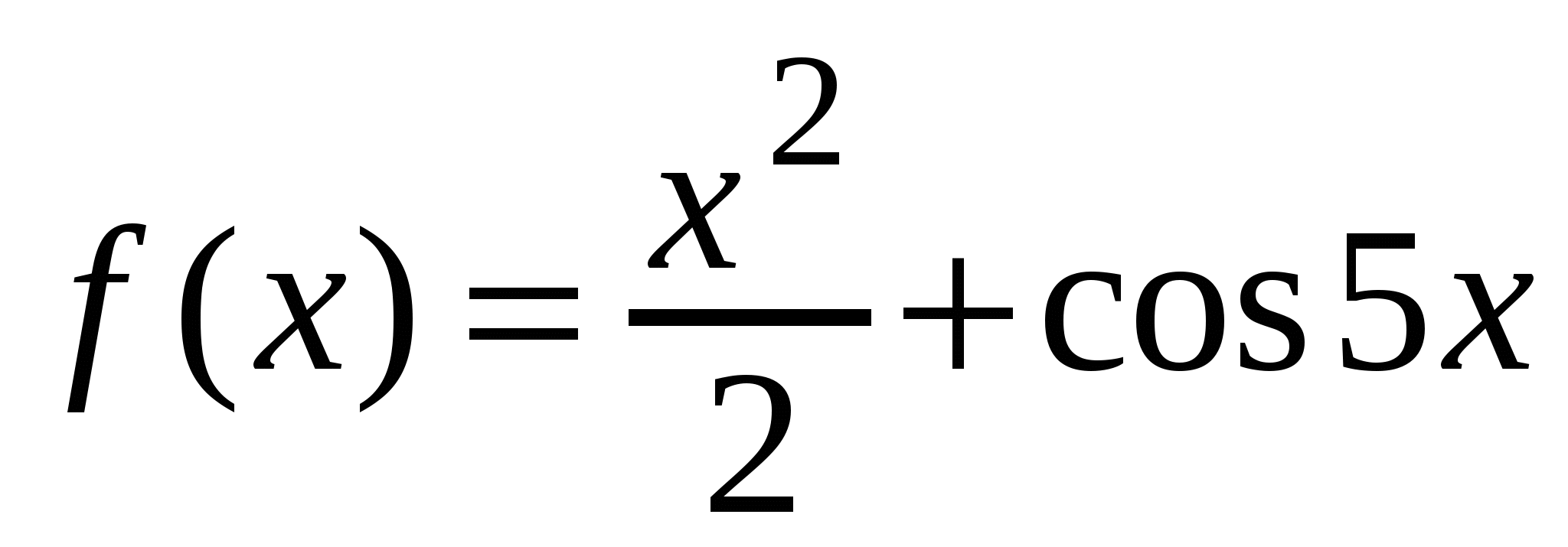 .
.
1) ![]()
3) ![]()
2) ![]()
4) ![]()
Найдите абсциссу точки, в которой касательная к графику функции
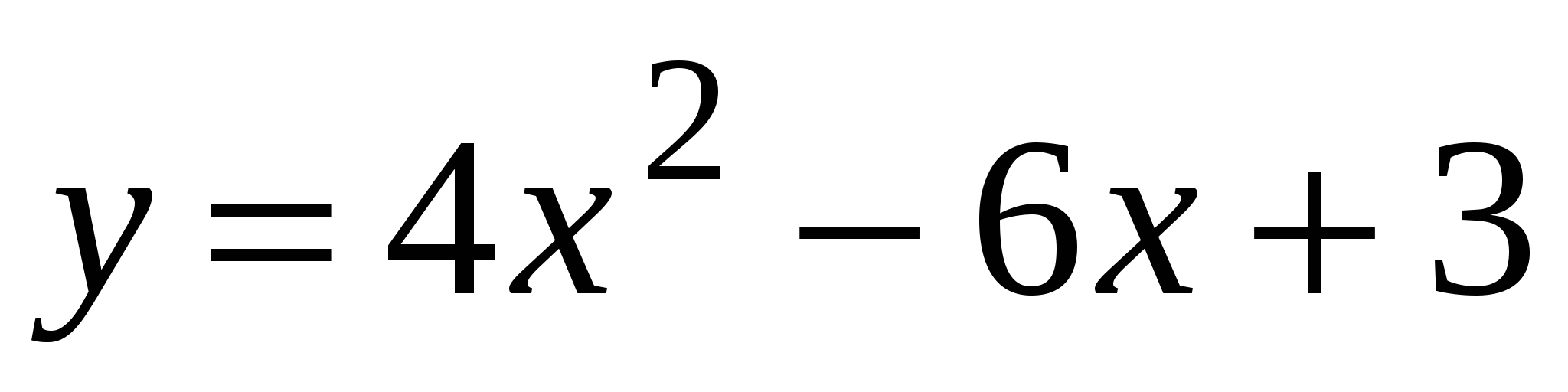 параллельна прямой
параллельна прямой 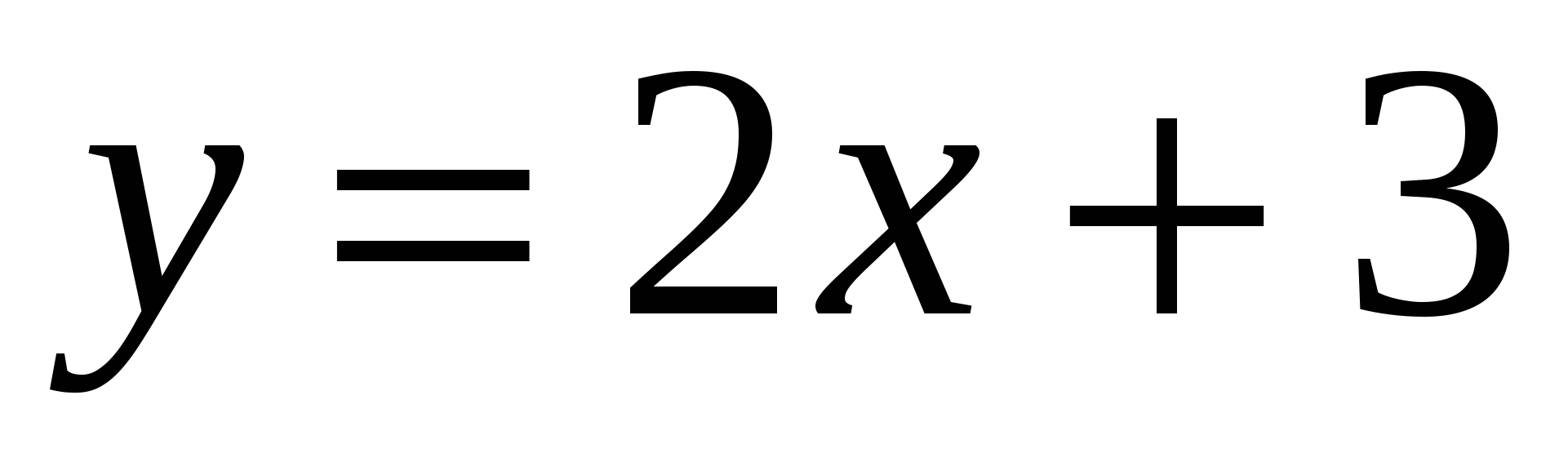 .
.
1)
– 2
2)
1
3)
2
4)
3
Найдите угловой коэффициент касательной, проведенной к графику функции
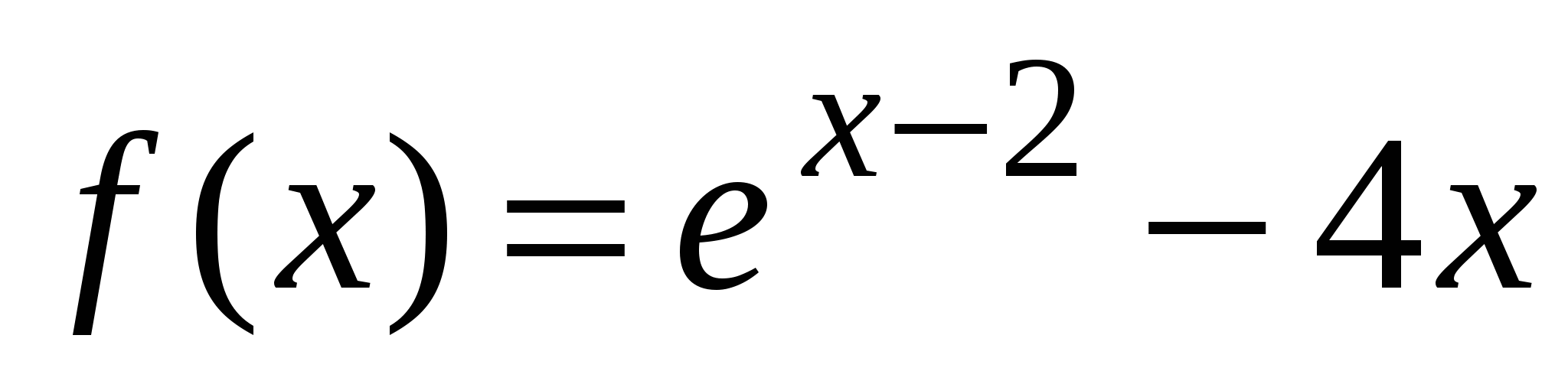 в точке с абсциссой
в точке с абсциссой 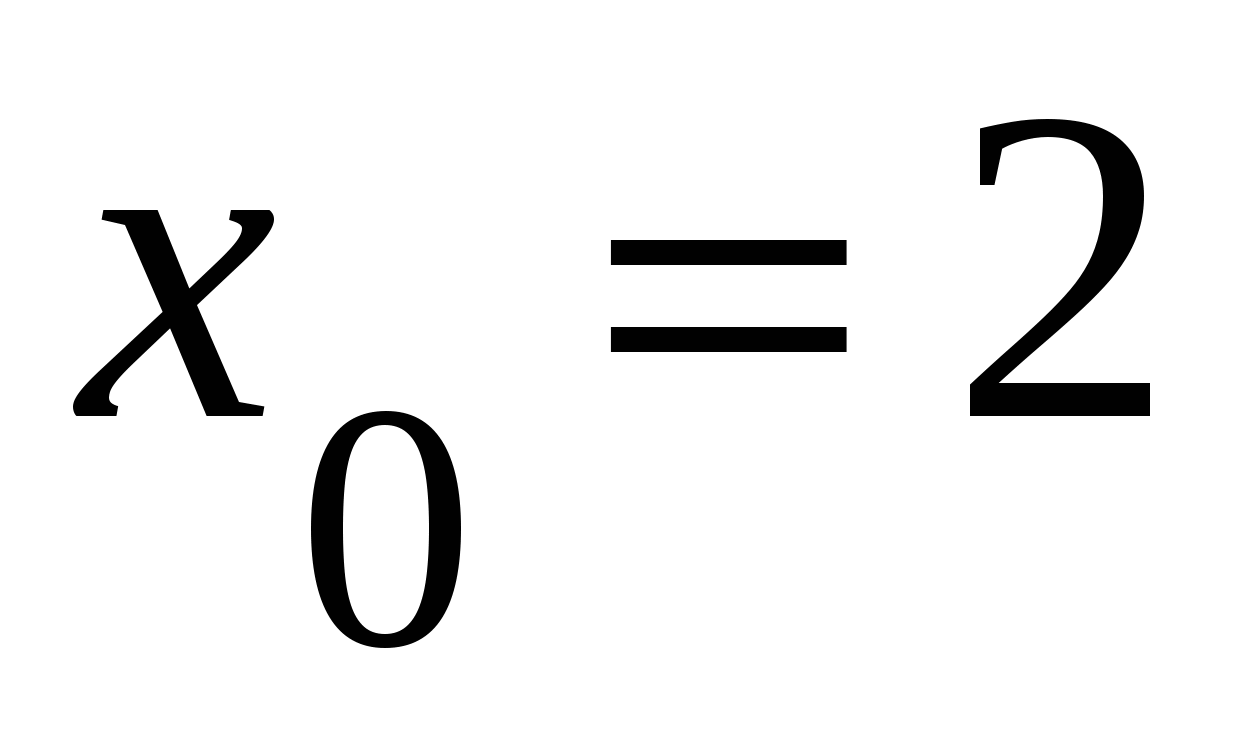 .
.
1)
![]()
2)
– 8
3)
– 3
4)
– 4
Чему равно значение производной функции в точке с абсциссой
 ?
?

Вариант 2
Найдите производную функции
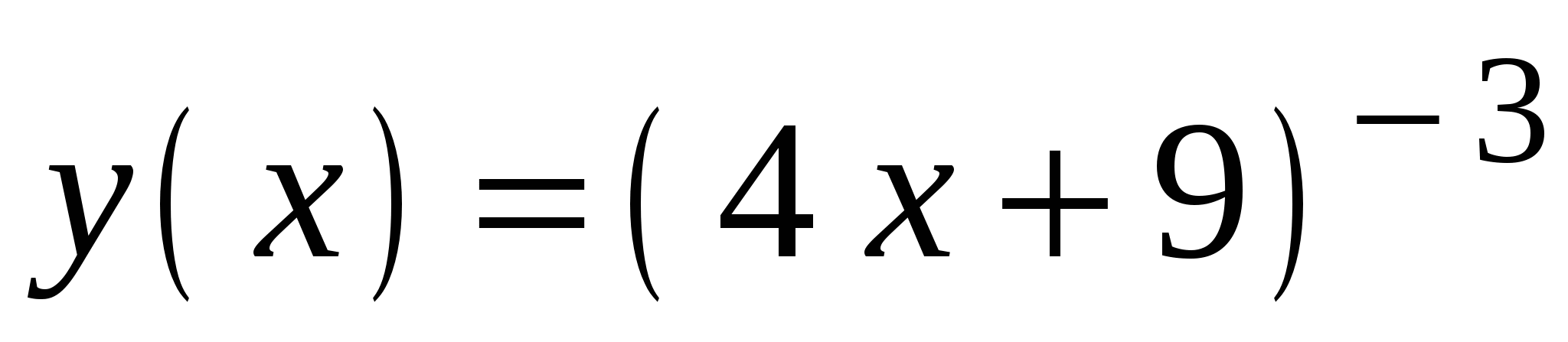 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
Найдите производную функции
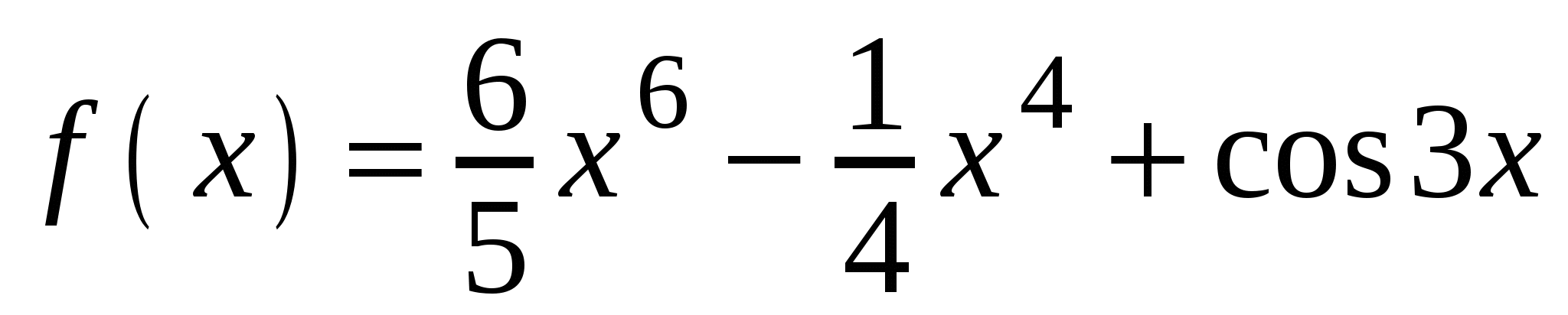 .
.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
К графику функции
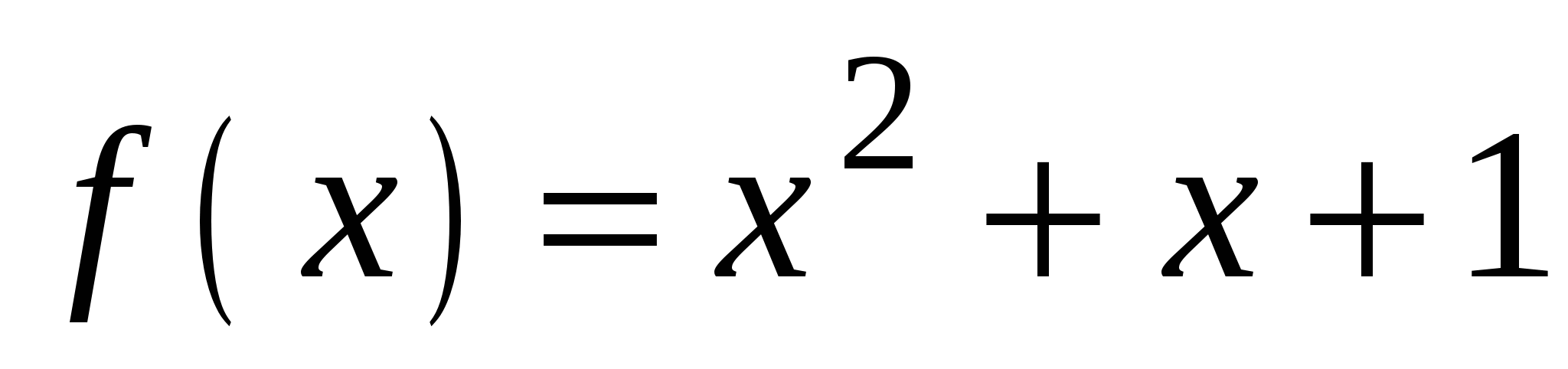 в точке с абсциссой
в точке с абсциссой 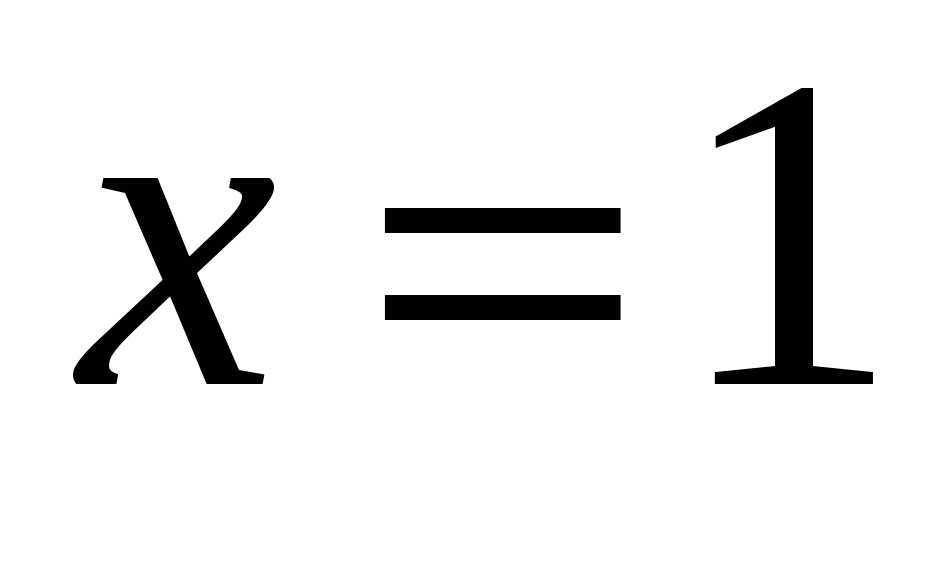 проведена касательная. Найдите абсциссу точки пересечения касательной с осью ОХ.
проведена касательная. Найдите абсциссу точки пересечения касательной с осью ОХ.
1)
0
2)
![]()
3)
![]()
4)
![]()
Укажите угол наклона касательной, проведенной к графику функции
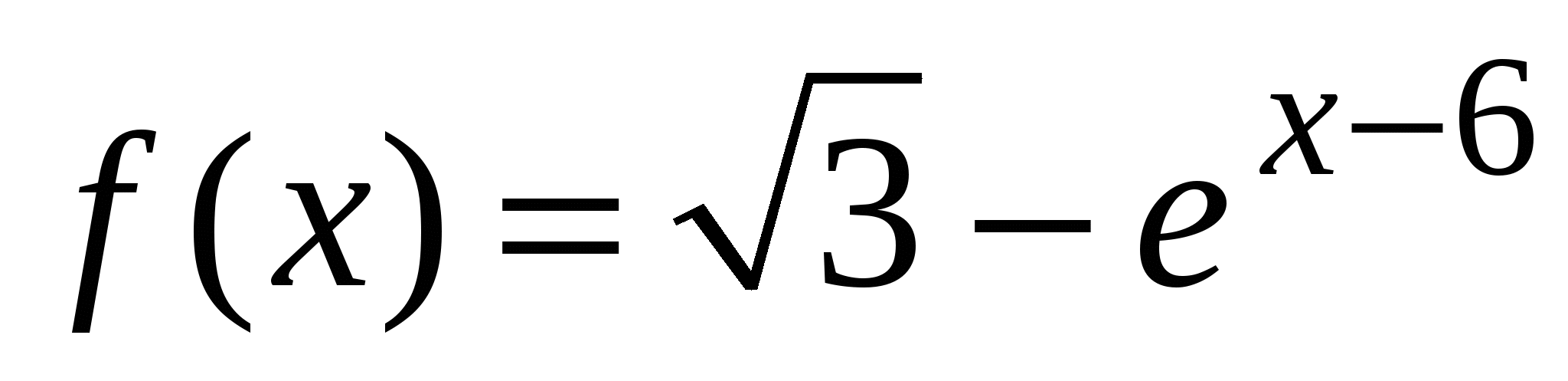 в точке с абсциссой
в точке с абсциссой 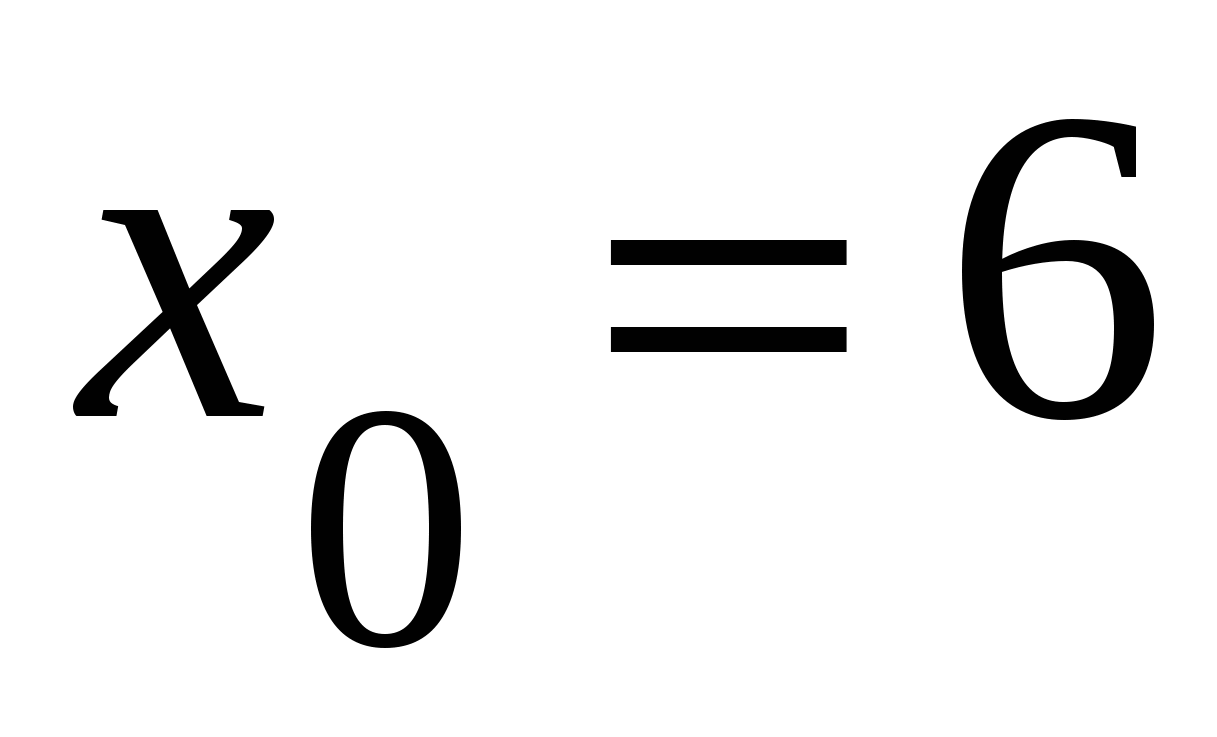 .
.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
На рисунке изображен график функции y = f(x) и касательная к нему. Найдите значение выражения
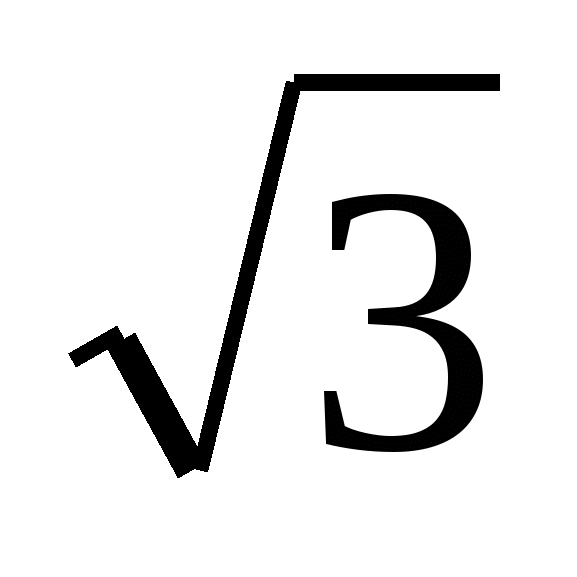 · f ′
· f ′ 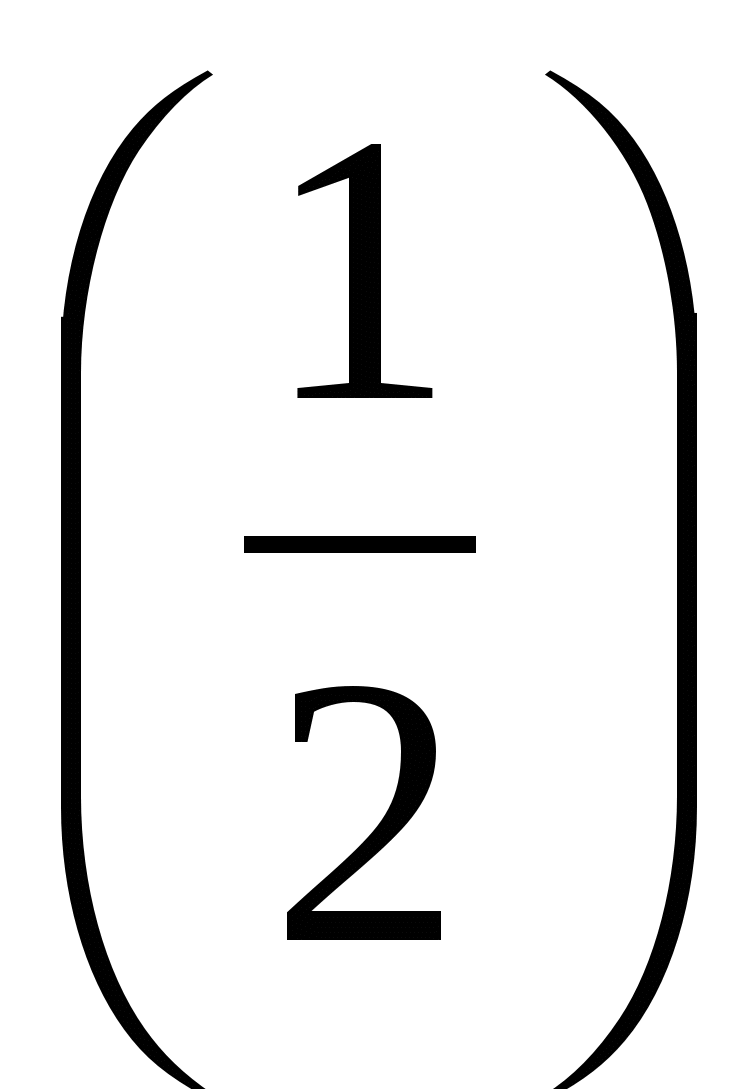 .
.
Вариант 3
Найдите производную функции
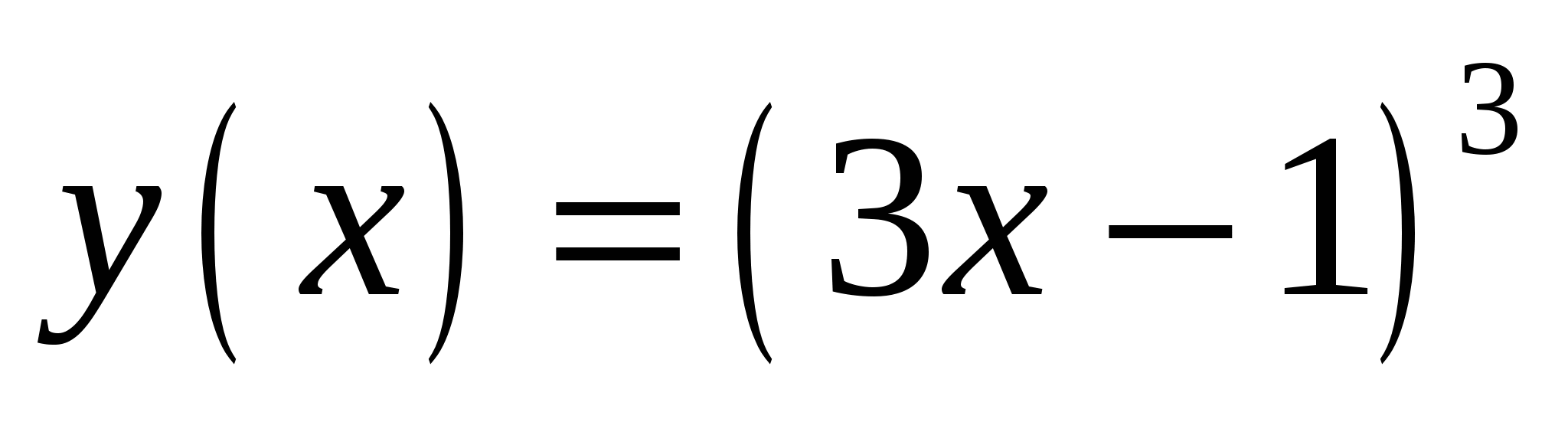 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
Найдите производную функции
 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
К графику функции
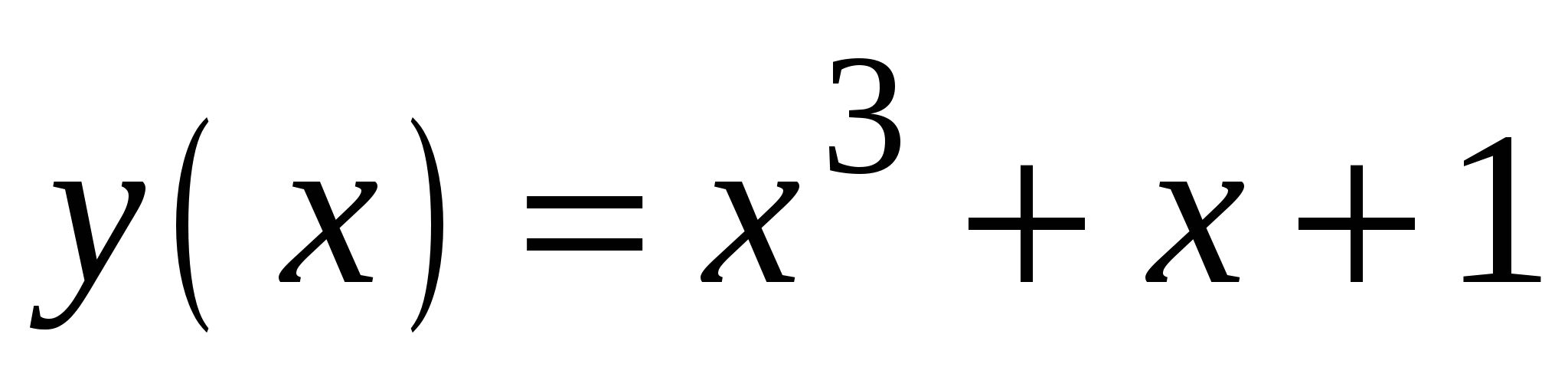 в точке с абсциссой
в точке с абсциссой 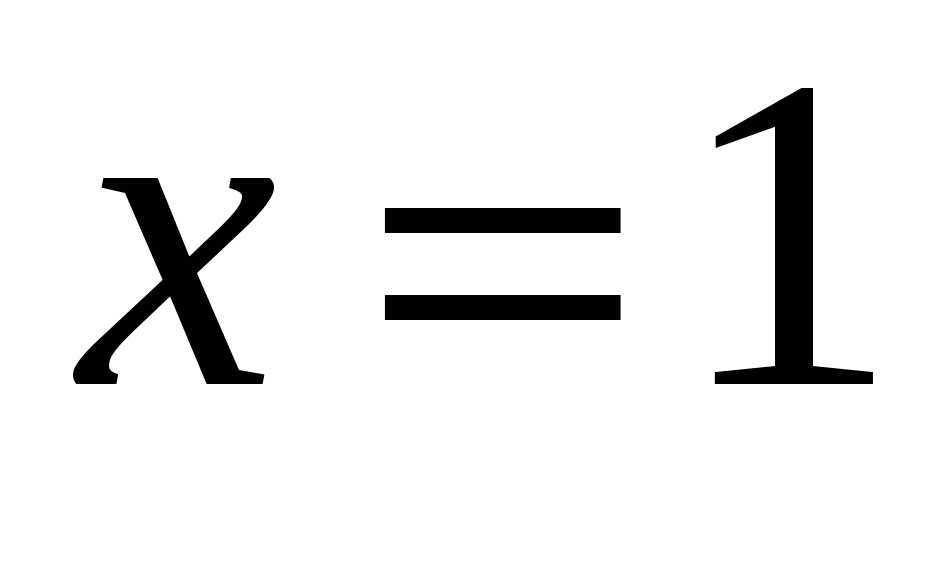 проведена касательная. Найдите абсциссу точки графика касательной, ордината которой равна 31.
проведена касательная. Найдите абсциссу точки графика касательной, ордината которой равна 31.
1)
7
2)
9
3)
10
4)
8
Укажите абсциссу точки графика функции
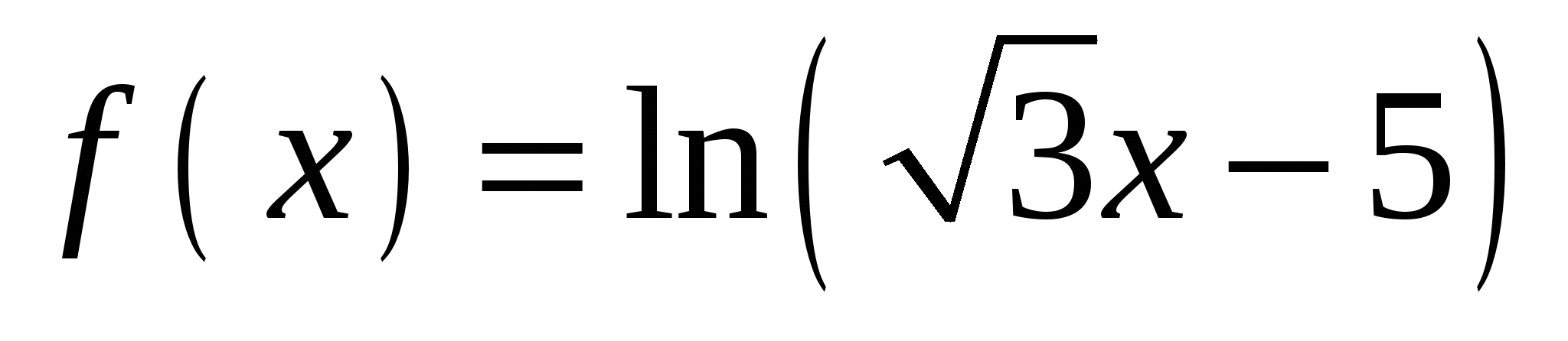 , в которой касательная составляет угол
, в которой касательная составляет угол 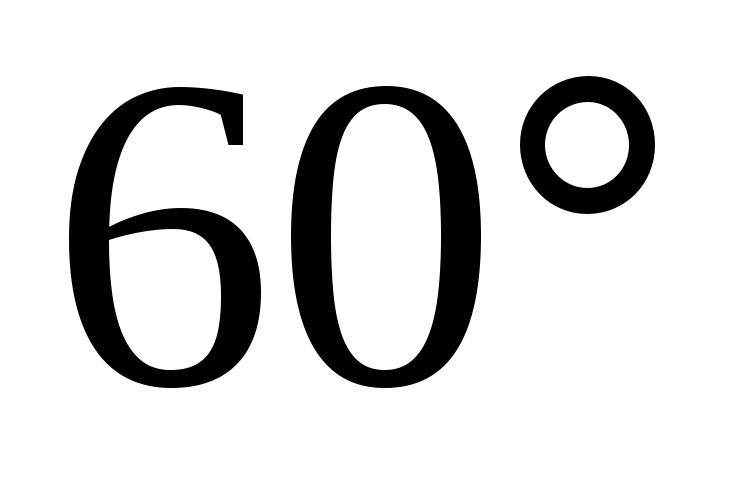 с положительным направлением оси абсцисс.
с положительным направлением оси абсцисс.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5. На рисунке изображен график функции ![]() и касательная к этому графику. Найдите значение выражения
и касательная к этому графику. Найдите значение выражения  .
.
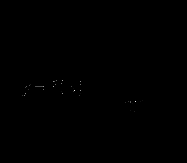
Вариант 4
Найдите производную функции
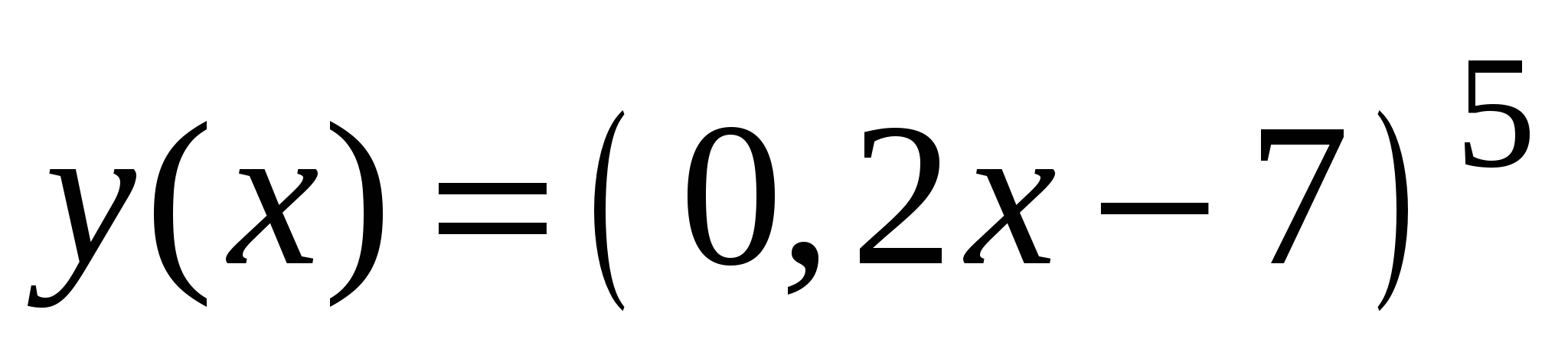 .
.
1)
![]()
3)
![]()
2)
![]()
4)
![]()
Найдите производную функции
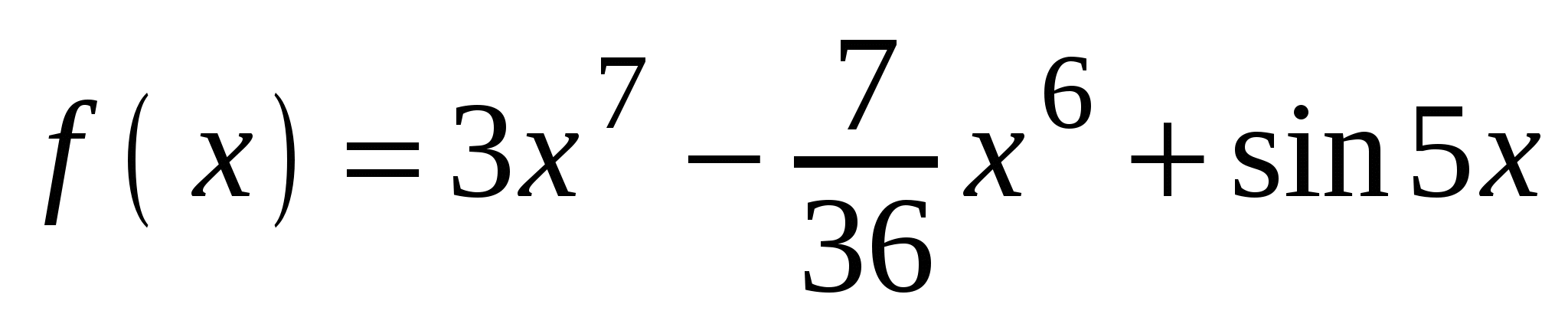 .
.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
К графику функции
 в точке с абсциссой
в точке с абсциссой 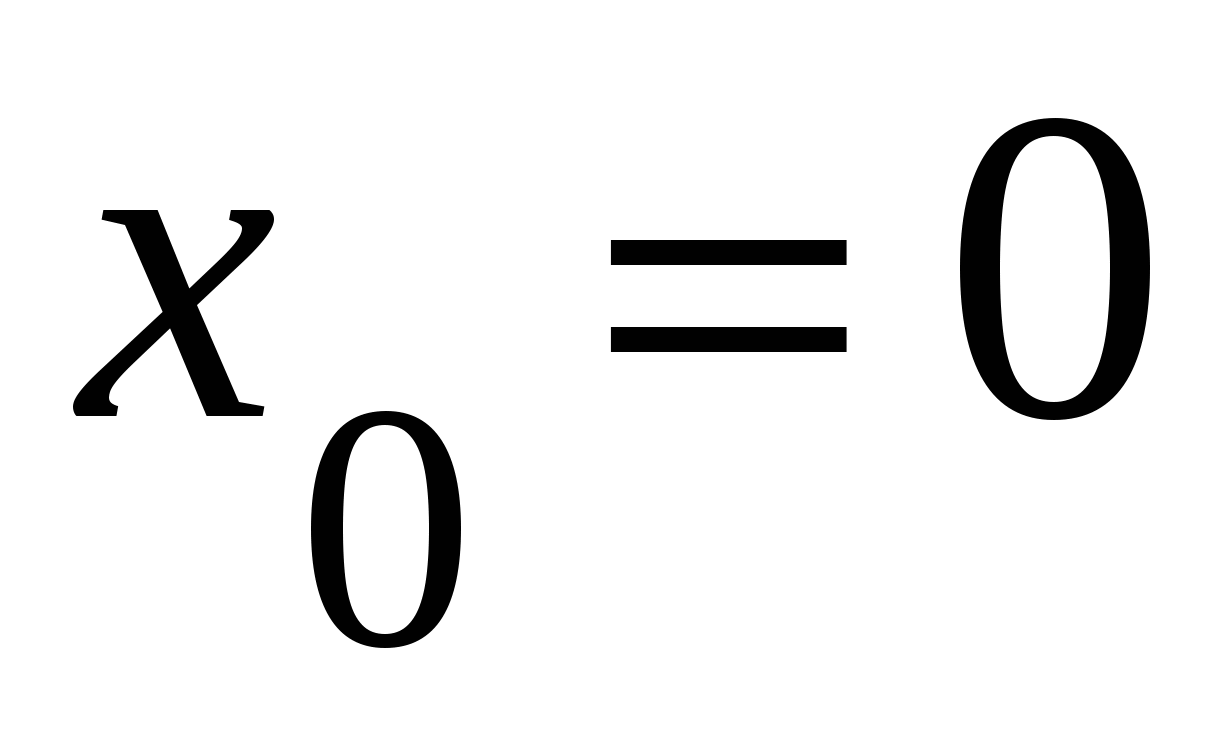 проведена касательная. Найдите абсциссу точки пересечения этой касательной с осью ОХ.
проведена касательная. Найдите абсциссу точки пересечения этой касательной с осью ОХ.
1)
4
2)
2
3)
– 2
4)
3
Определите абсциссу точки графика функции
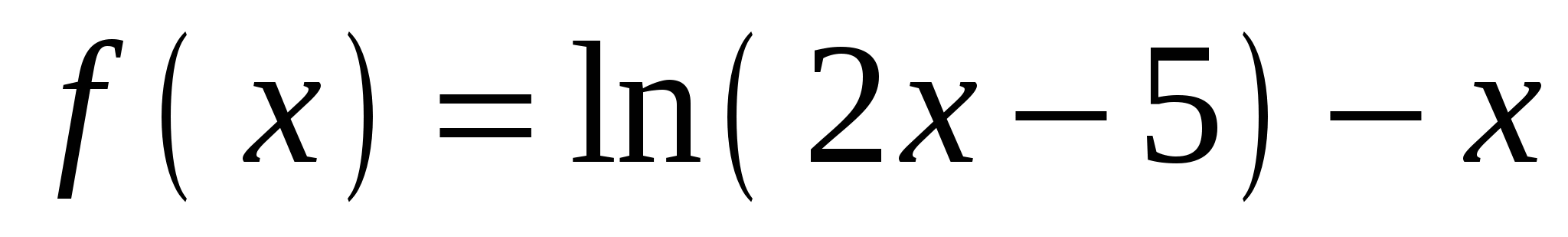 , в которой касательная параллельна оси Ox.
, в которой касательная параллельна оси Ox.
1)
6
2)
2
3)
3
4)
3,5
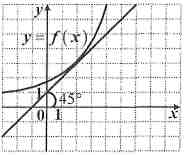
На рисунке изображен график функции y = f(x) и касательная к нему. Найдите значение производной f '(2).
Ответы:
Номер задания
1
2
3
4
5
Вариант 1
2
3
2
3
− 1
Вариант 2
2
4
1
3
− 3
Вариант 3
2
3
4
2
1
Вариант 4
1
2
4
4
1
Уровень С
Вариант 1
Прямая пересекает ось абсцисс при
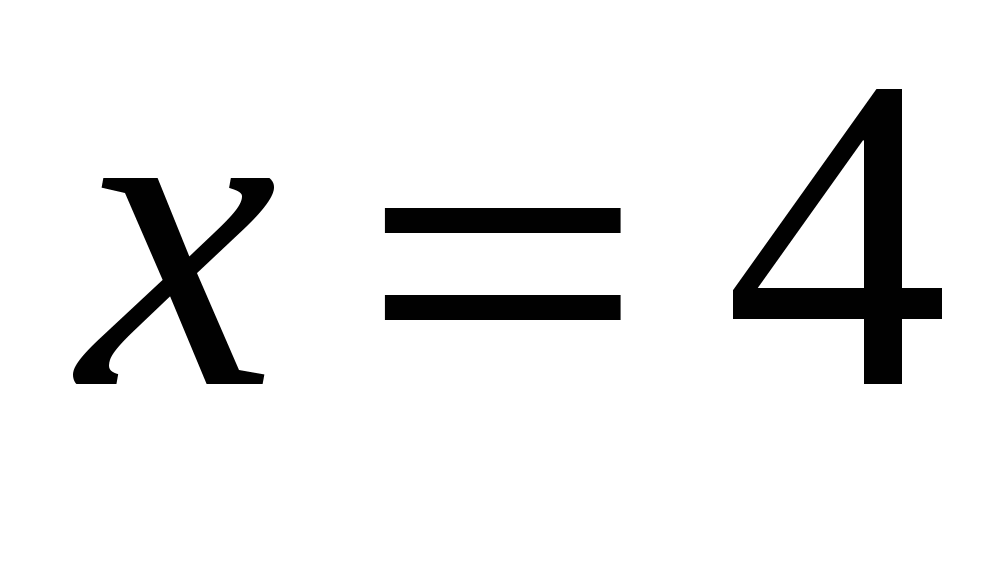 , касается графика функции
, касается графика функции 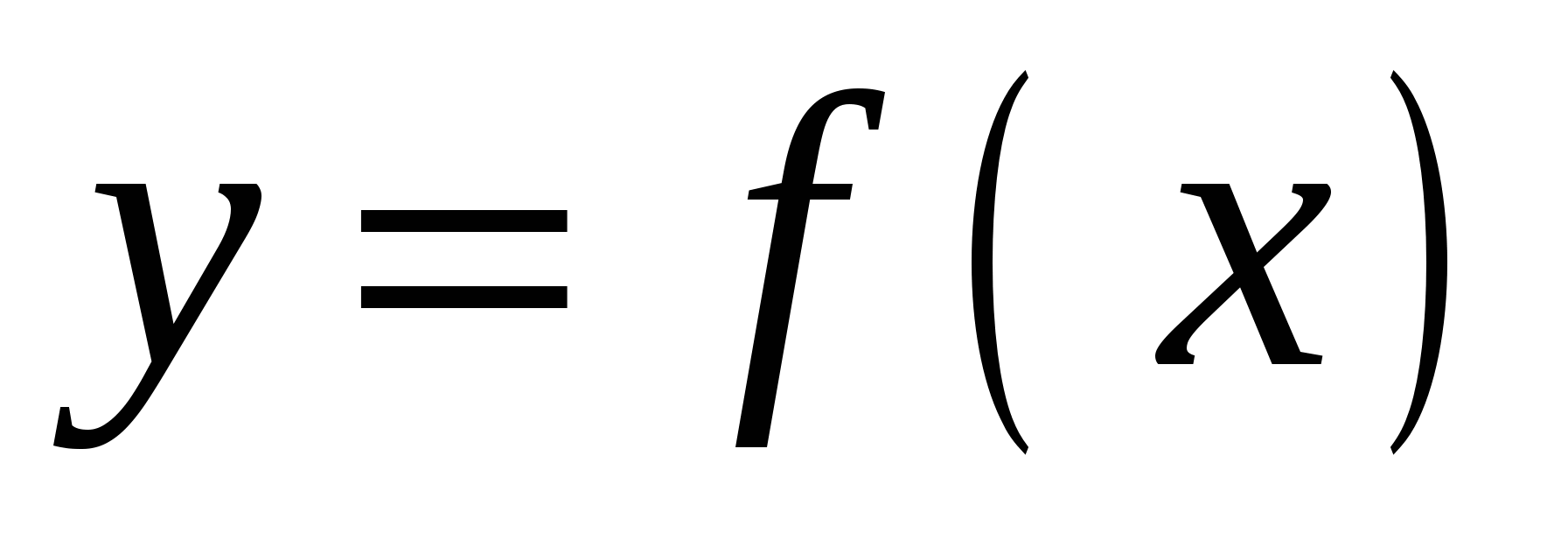 в точке
в точке 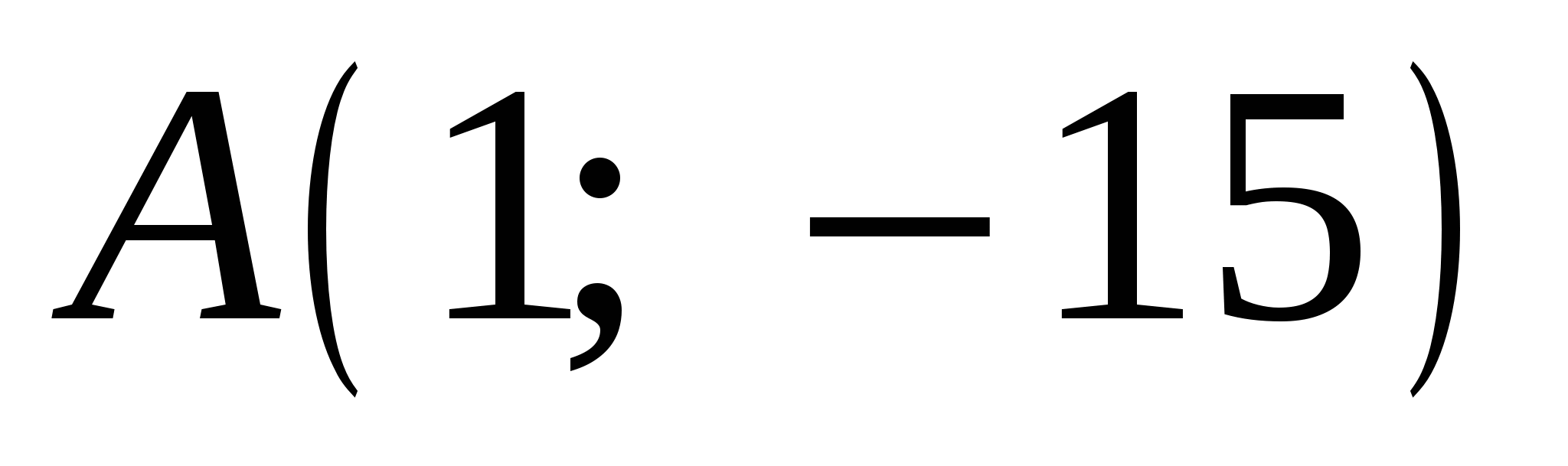 . Найдите
. Найдите 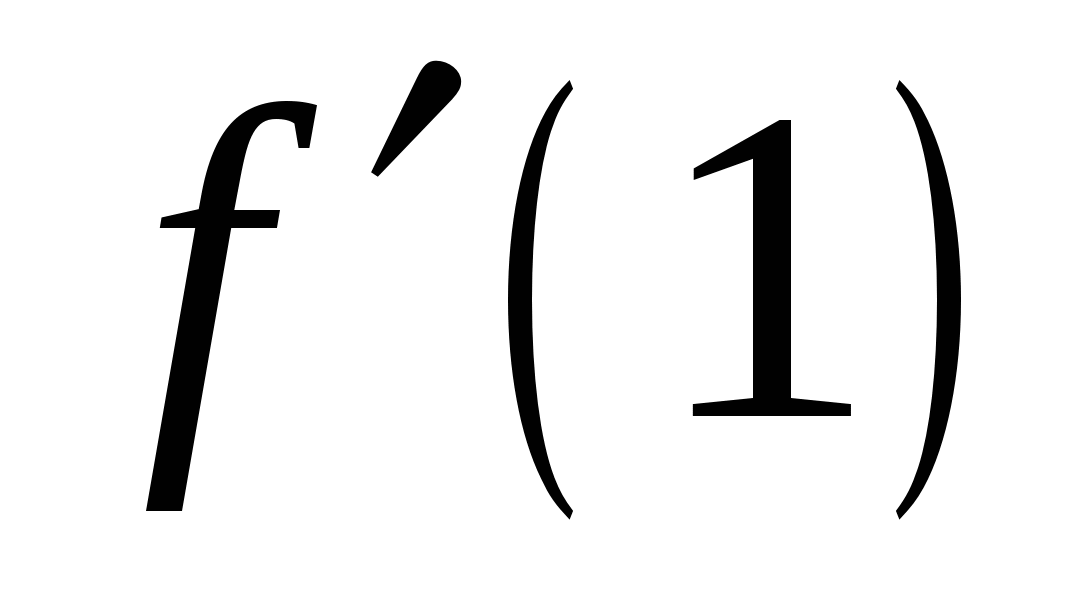 .
.Ф
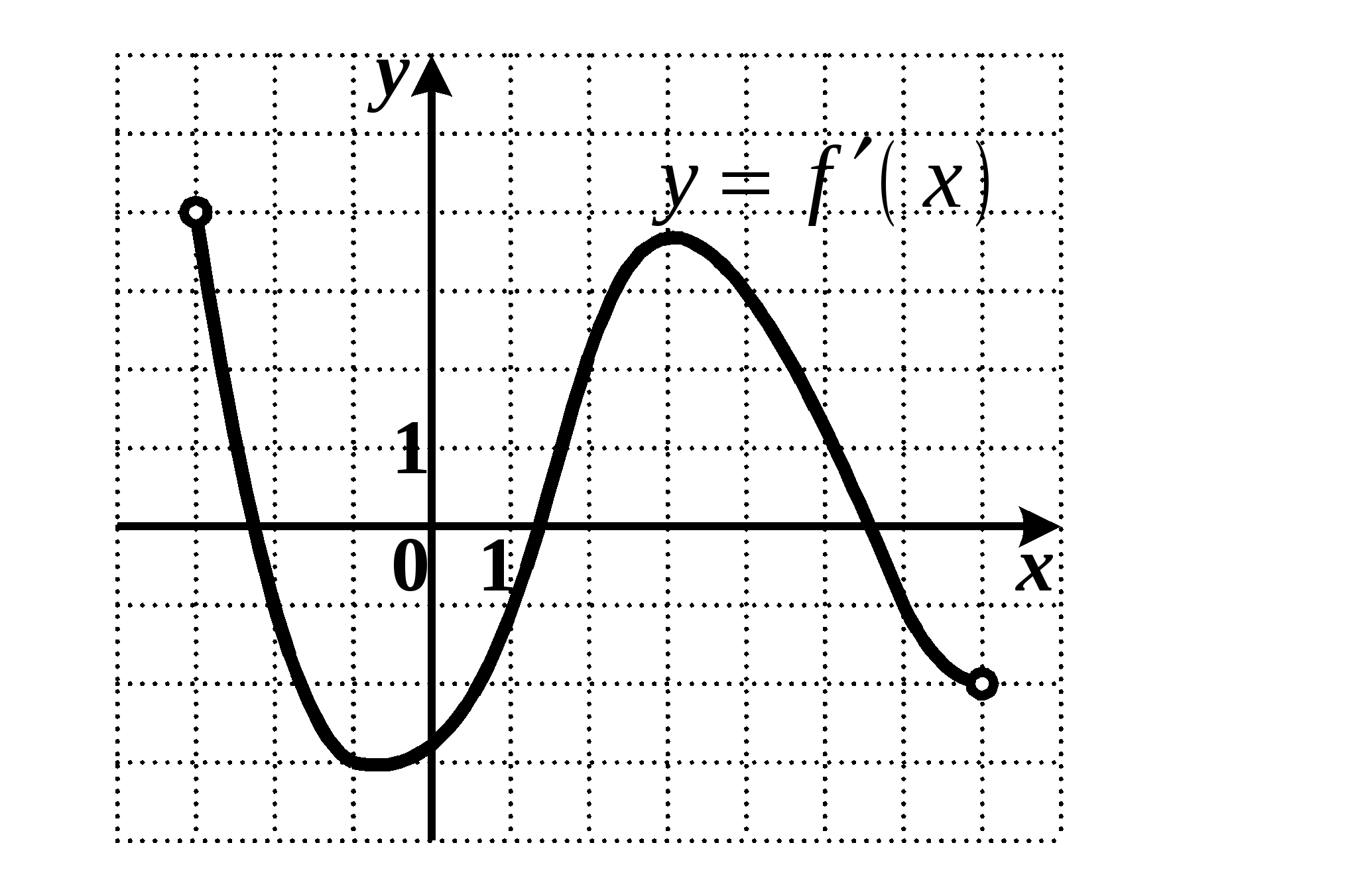 ункция
ункция 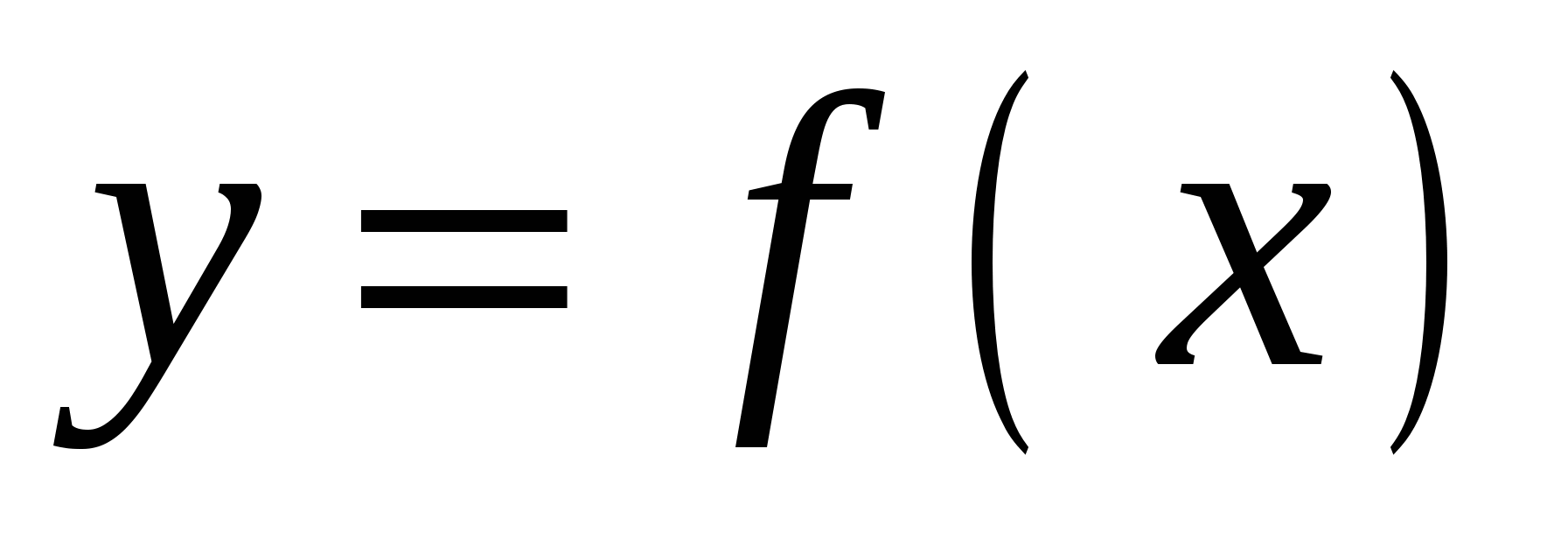 определена на промежутке
определена на промежутке 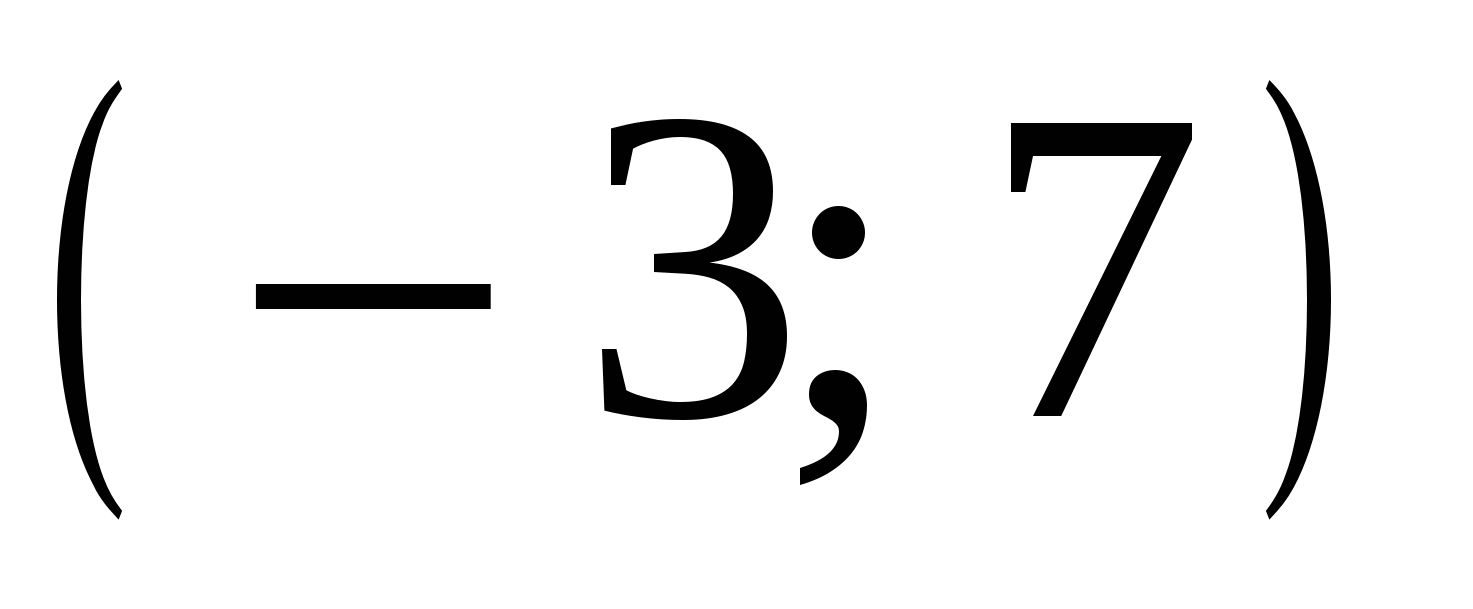 . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной 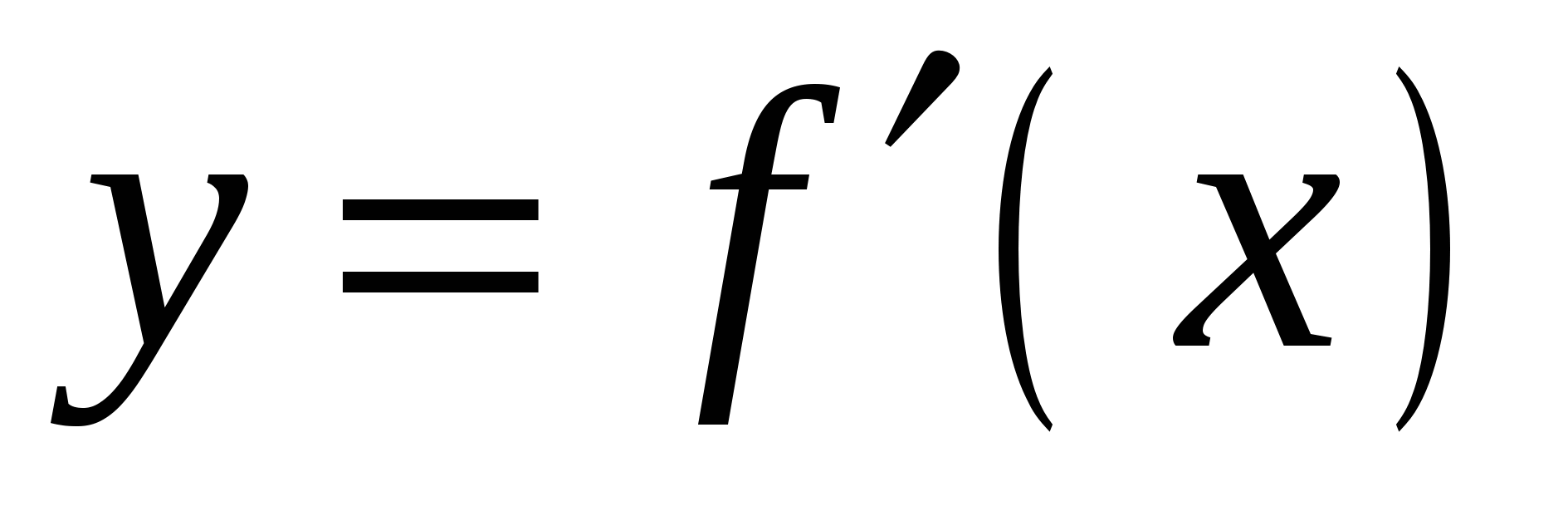 , определите количество касательных к графику функции
, определите количество касательных к графику функции 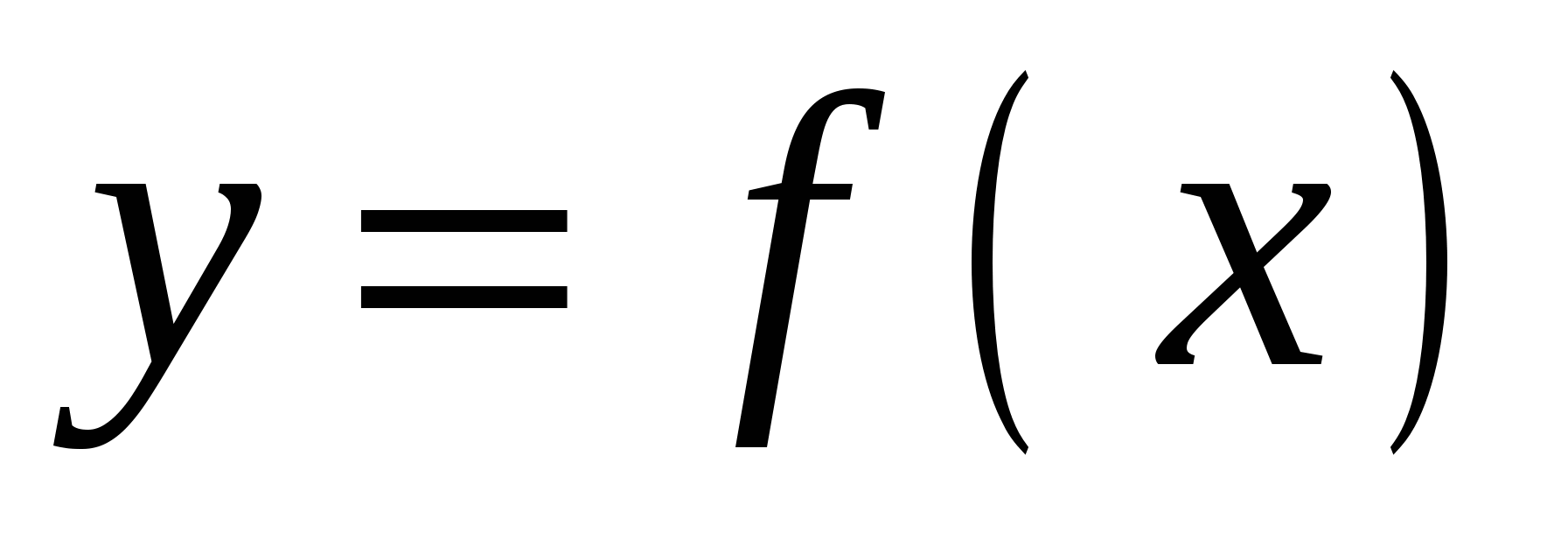 , которые составляют угол
, которые составляют угол 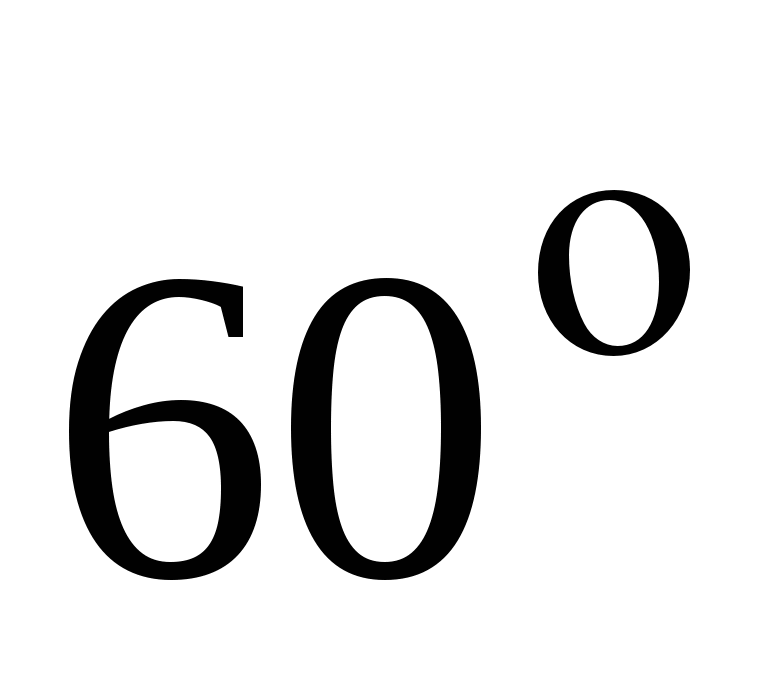 с положительным направлением оси Ox.
с положительным направлением оси Ox.
Дана функция
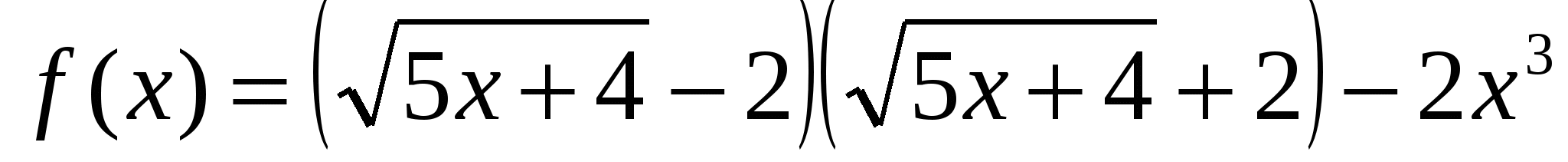 . Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой
. Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой 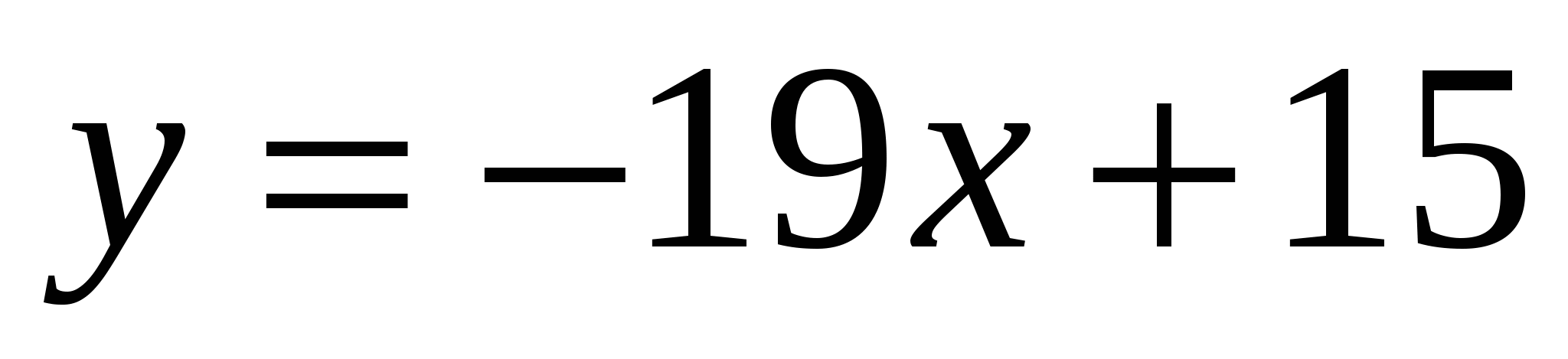 или совпадают с ней?
или совпадают с ней?
Вариант 2
Прямая пересекает ось ординат при
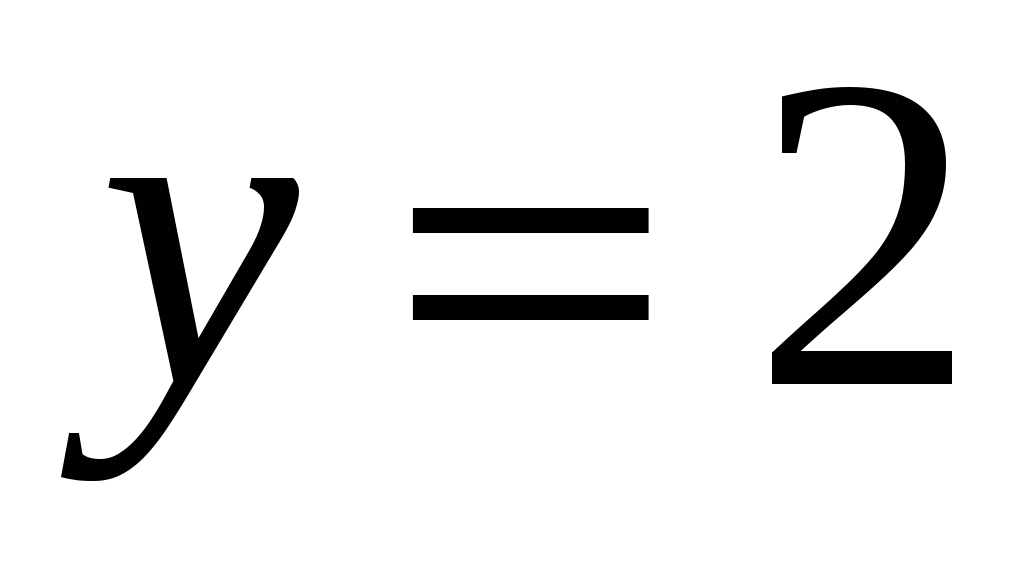 , касается графика функции
, касается графика функции 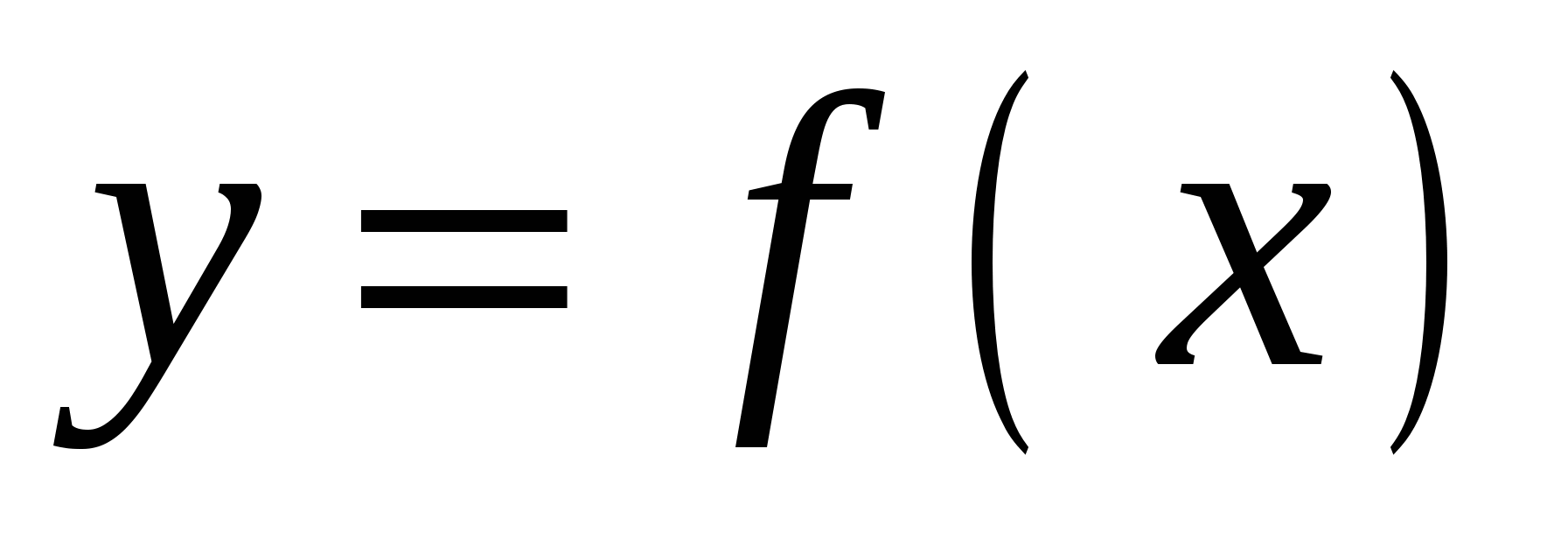 в точке
в точке 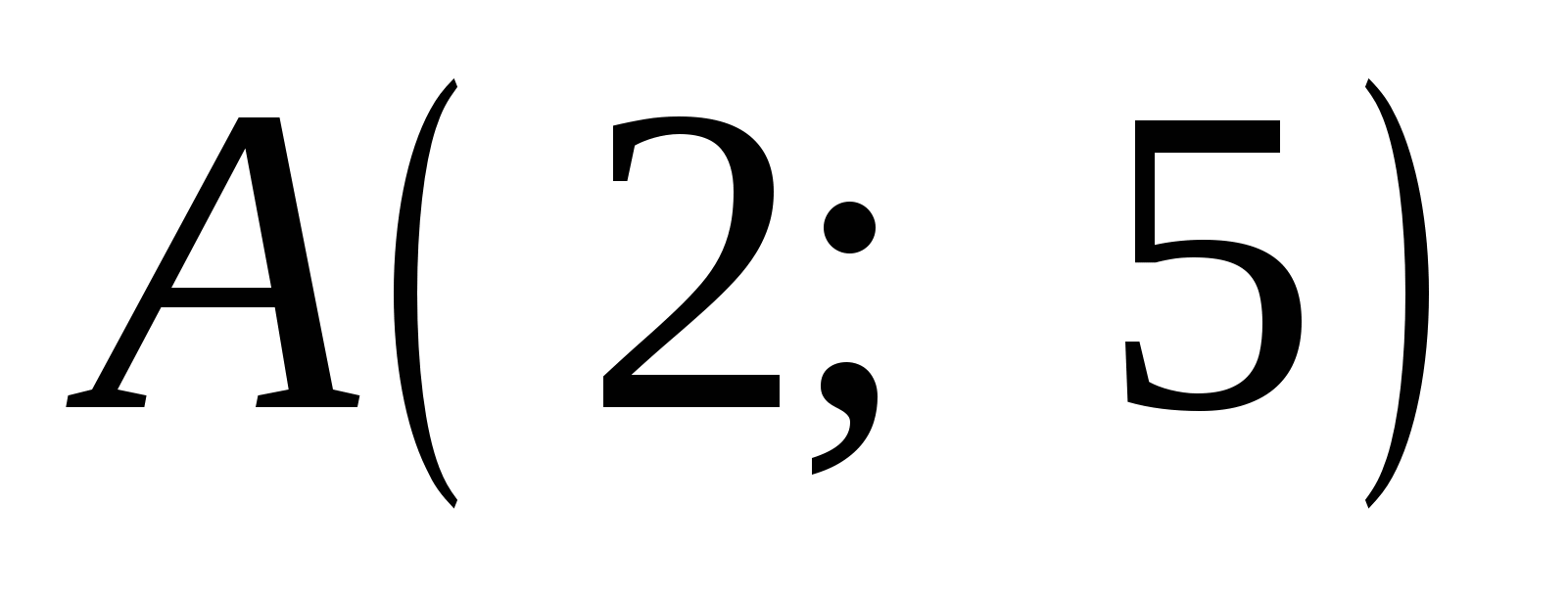 . Найдите
. Найдите 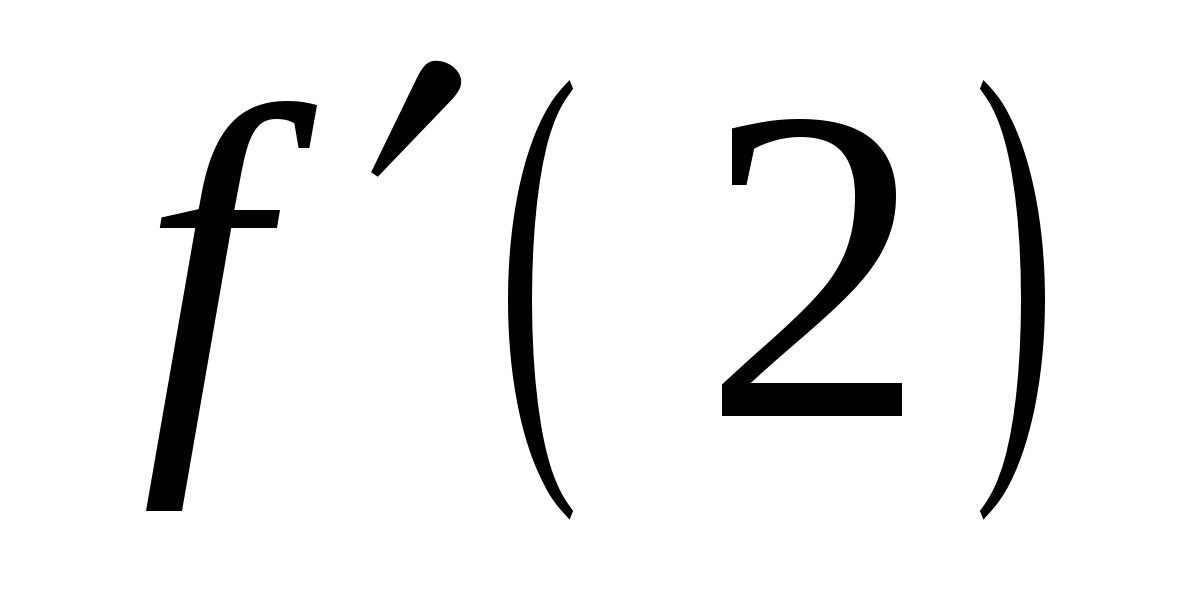 .
.
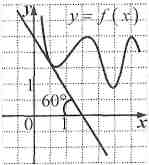
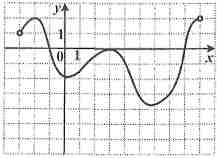
Функция у = f (x) определена
на промежутке (- 3; 9).
Используя изображенный на
рисунке график производной
y = f '(x), определите
количество касательных к графику
функции у = f(х), которые составляют угол 120°
с положительным направлением оси Ох.
Дана функция
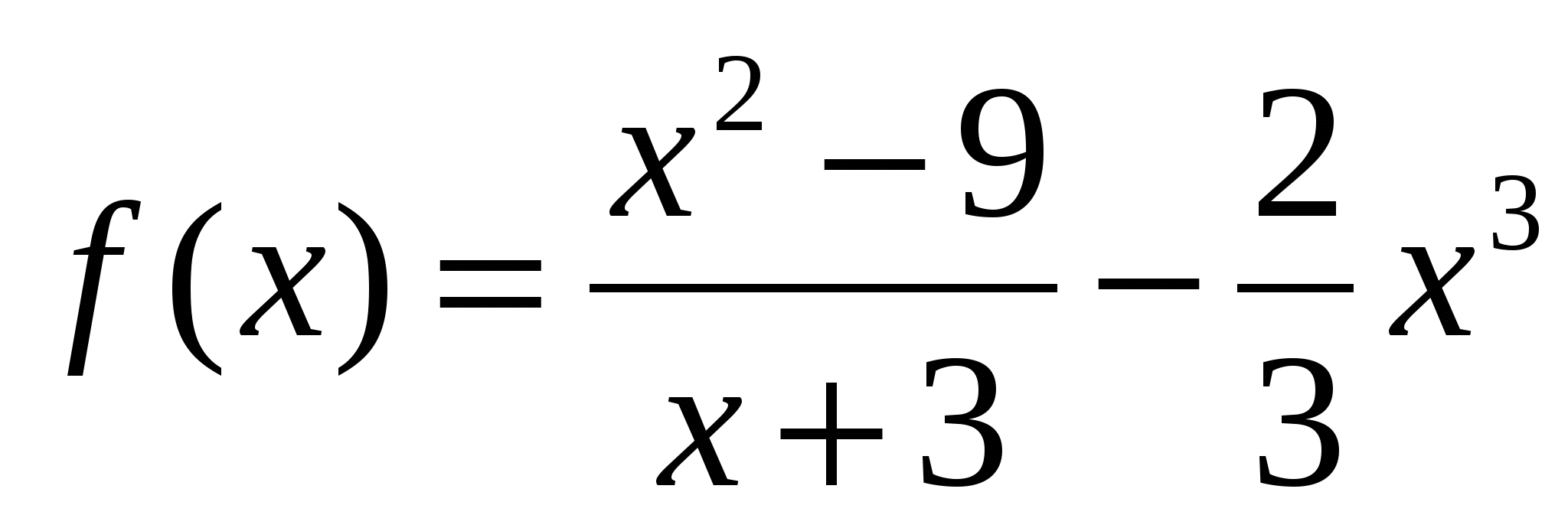 . Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой
. Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой 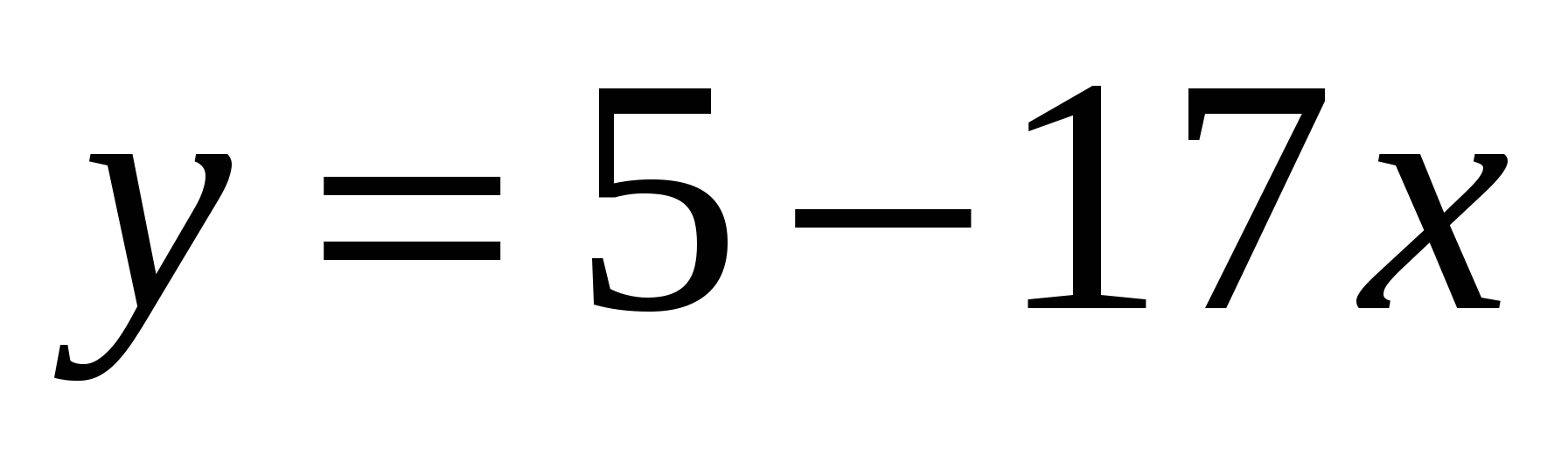 или совпадают с ней?
или совпадают с ней?
Ответы:
Номер задания
1
2
3
Вариант 1
5
3
2
Вариант 2
1,5
4
3
Решение задания № 3
Вариант 1
Дана функция ![]() . Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой
. Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой ![]() или совпадают с ней?
или совпадают с ней?
Решение.
1) ![]() ;
;
2) ![]() ;
;
![]() ;
;
3) f ′(x) = 5 – 6x2;
4) Так как угловые коэффициенты параллельных прямых равны, а угловой коэффициент касательной равен значению производной функции в точке касания, то:
5 – 6x2 = – 19;
– 6x2 = – 24;
x2 = 4;
x = ![]() ;
;
5) –2 ![]() .
.
Ответ: 2.
Вариант 2
Дана функция ![]() . Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой
. Каковы абсциссы всех точек графика этой функции, касательные в которых параллельны прямой ![]() или совпадают с ней?
или совпадают с ней?
Решение.
1) ![]() ;
;
2) ![]() ;
;
![]() ;
;
3) f ′(x) = 1 – 2x2;
4) Так как угловые коэффициенты параллельных прямых равны, а угловой коэффициент касательной равен значению производной функции в точке касания, то:
1 – 2x2 = – 17;
– 2x2 = – 18;
x2 = 9;
x = ![]() ;
;
5) –3 ![]() .
.
Ответ: 3.
Во время выполнения работы учитель, при необходимости, помогает учащимся первой группы (уровень А) выполнять задания наводящими вопросами. Максимальная оценка, которую могут получить учащиеся этой группы – «4», при условии того, что все задания выполнены верно. Оценка «3» выставляется в случае, если правильно выполнено 3 – 4 задания из 5 возможных.
Соответственно, максимальная оценка, которую могут получить учащиеся второй группы (уровень В) – «5». Оценка «3» выставляется за 3 верно решенных задания, «4» – за 4 верно решенных задания, «5» − за все верно решенные задания (их всего 5).
Варианты заданий уровня С содержат 2 задания повышенного уровня сложности с кратким ответом и 1 задание повышенного уровня сложности с развернутым ответом. Максимальное количество баллов равно 4 (задание №2 оценивается при верном решении в 2 балла), и за это выставляется оценка «5». 3 балла – «4».
V этап урока (5 минут) - подведение итогов, комментарии по домашнему заданию.
Учитель отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет оценки. Основной части класса оценки будут объявлены на следующем уроке.
В качестве домашнего задания учащиеся получают по одному варианту из краевой диагностической работы (январь 2009 г.). и обмениваются в пределах своей группы вариантами самостоятельной работы.
Используемая литература:
Алгебра и начала анализа. 10 – 11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. – 9 изд., перераб. – М. : Мнемозина, 2008.
Алгебра и начала анализа. 10 – 11 классы. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А. Г. Мордкович. и др.] – 9 изд., перераб. – М. : Мнемозина, 2008.
Тестовые задания для подготовки к ЕГЭ-2009 по математике / Под ред. Е. А. Семенко. – Краснодар: «Просвещение-Юг», 2009.
Математика. Подготовка к ЕГЭ-2010/Под редакцией Ф. Ф. Лысенко, С. Ю. Кулабухова. – Ростов-на-Дону: Легион-М, 2009.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ