Конспект урока Геометрии "Площадь и объём цилиндрических тел"











 Урок 2
Урок 2
Тема: Площадь и объём цилиндрических тел
Тип учебного занятия:
Обобщение и систематизация знаний и способов деятельности.
Цели урока:
Организовать деятельность учащихся по обобщению и систематизации понятия цилиндрическое тело.
Создать условия для осмысления учащимися общих формул вычисления площади поверхности призмы и кругового цилиндра, дать обобщенную формулу объема цилиндрических тел.
С помощью математического диктанта выявить типичные ошибки и пробелы в знаниях с целью их последующего устранения.
Обеспечить развитие у учащихся умений сравнивать познавательные объекты, продолжить развитие пространственного мышления.
Форма учебного занятия:
Классический урок с элементами исследовательской работы.
Оснащение урока:
модели призмы, цилиндра, параллелепипеда.
учебник «Геометрии 10 – 11 кл.» под редакцией Л.С. Атанасян.
Таблицы «Объемы», «Объемы цилиндрических тел».
Ход урока:
Организация занятия.
Проверка готовности учащихся к занятию, постановка целей и задачи урока. Тема урока записывается в тетради и на доске.
Проверка домашнего задания:
Записать формулы площади треугольника, параллелограмма, трапеции, прямоугольника, круга.
2) решение задач по карточкам № 1, 2, 3, 4
3) Математический диктант
геометрическое тело, поверхность которого ограничена конечным
числом многоугольников
2- многогранник, который состоит из двух параллельных и равных
шестиугольников и шести прямоугольников.
Многогранник, который ограничен квадратом и четырьмя
равнобедренными треугольниками с общей вершиной.
если у треугольника все стороны равны, то его площадь находится по формуле…
чтобы найти площадь поверхности прямоугольного параллелепипеда
с измерениями а, в и с нужно…
6- многогранник, боковыми гранями которого являются трапеции, а основания - два подобных многоугольника.
Ответы: 1 – многогранник, 2 – шестиугольная призма; 3- правильная четырехугольная пирамида; 4 - 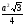 ; 5 – (ав+ вс+ас)·2; 6 – усеченная пирамида.
; 5 – (ав+ вс+ас)·2; 6 – усеченная пирамида.
Проверка решений задач, формул, диктанта. Итоги проверки.
Изучение нового материала.
Сообщение учащегося (историческая справка)
.Общее понятие цилиндрического тела (по таблице «Цилиндрические тела»).
Площадь поверхности любого цилиндрического тела:
Sпов=2Sосн. + Sбок.
4. Решение задачи №539 из учебника.
№ 539 стр. 123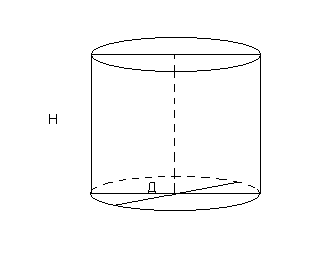
Дано:
цилиндр
Д=1,5 м
Н=3 м
На 1м2 – 200г
M - ?
Анализ задачи:
Если на 1м2 – 200г краски, но необходимо знать площадь поверхности всего бака.
Sпов.ц. = 2S осн. + S бок.
S осн. = S круг. = 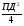
S бок. = ПД • Н
m = 200г • S пов.
Решение:
S п.ц. =
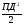 + ПДН = ПД (
+ ПДН = ПД (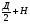 ) S п.ц. = П•1,5 (
) S п.ц. = П•1,5 (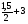 ) = 5,625П
) = 5,625П
S п.ц. = 3, 14 • 1, 5 (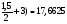 m = 200 • 5,625 = 1,125Пкг
m = 200 • 5,625 = 1,125Пкг
m = 200 • 17,6625 = 3532,5 ≈ 3,5кг Ответ: 1,125Пкг
5.Работа с учебником, стр.140 и таблицей «Объем цилиндрических тел».
Общие понятия
Свойства объема
Объем прямоугольного параллелепипеда
Объем призмы и объем кругового цилиндра
Вывод: объем цилиндрического тела равен произведению площади основания на высоту.
Первичное закрепление материала при решении задач.
1. Задача №663
Найти объем правильной n-угольной призмы, у которой каждое ребро равно а. а) n=3, б) n=4, в) n=6.
Решение задачи проводится учащимся с объяснением, более подготовленные учащиеся решают задачу самостоятельно (решив задачу, и проверив ее решение у преподователя, помогают тем, кто нуждается в пояснении).
2. Задача №668.
Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметром в 18 метров и высотой 7 метров, если плотность нефти равна 0,85 г/см3
По заданию № 668 проводится анализ задачи, и записываются основные формулы на доске. Решение – самостоятельно. (Кто не сможет решить задачу, разбираем решение)
Задача № 670 – для самостоятельного решения сильным учащимся
Свинцова труба (плотность свинца 11, 4 г/см3) с толщиной стена 4 мм имеет внутренний диаметр 13 мм. Какова масса трубы, если ее длина равна 25 м?
(Для всех задач, предложенных для самостоятельной работы, проверка осуществляется по образцам).
Подведение итогов:
общая характеристика работы класса,
итоги математического диктанта, анализ самостоятельной работы учащихся.
VII. Домашнее задание
Повторить формулы площади поверхности и цилиндрических тел, повторить определение следующих пространственных тел: пирамиды, конуса, усеченной пирамиды, усеченного конуса. Решить задачу №663 (б).
VIII.Рефлексия.
Самооценка работы на уроке, недостатки и положительные стороны урока..
Каждый учащийся определяет свою точку по степени усвоения материала данного урока и на оценочных листах проставляют свои точки
const
max1
max2
min1
min2
Min3
const – урок как урок
min1 – «не понял!»
min2 – не все понял, но хочу понять
max1 – не все понял, прошу помощи!
max2 – понял!
Min3– не хочу понимать!
Приложения к уроку:
Vц. т = S осн. • Н
Цилиндрическое тело
Призма Круговой цилиндр
V = S осн. • Н Vц. т = S осн. • Н = ПR2 • Н
Прямоугольный
Параллелепипед
V = S осн. V = S осн. • Н = а•в •н
Или
V=а•в•Н
Куб
V=а3
Историческая справка (сообщение учащегося по историческому блоку):
Для того, чтобыопределить объем камня, необходимого для строительства великих пирамид (Хеопса, Хефрена и Минерита) в Гизе, древними зодчими нужно было уметь рассчитывать объем пирамиды;
Уличить недобросовестных ювелиров Архимеду помог открытый им в ванне «эвристический закон»: объем погруженного в воду тела можно. определить по вытесненному телом объему воды;
Поиску формулы для определения емкости винных бочек посвятил свой труд известный математик и астроном И.Кеплер. Его научный труд под названием «Новая стереометрия винных бочек» вышел в свет в 1615г. Эти примеры иллюстрируют тот факт, что понятие объема и простейшие вычисления, связанные с нахождением объемов, возникли из практических потребностей людей: измерения объема строительных работ, определение вместимости различных емкостей, нахождение массы и плотности предметов и т.д. До возникновения интегрального исчисления способы вывода формул объемов разных тел были самыми разнообразными.
Так, для вывода объема цилиндра использовали метод аппроксимации
для объема подобных тел – принцип Кавальери, для усеченных тел – формулы Симпсона.
Интеграл помог облегчить вывод формул объемов тел путем их унификации.
Исторический блок.
.
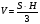
Kepler J (1615г) 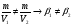
Метод аппроксимации
Принцип Кавальери  V
V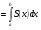
Формулы Симпсона
Блок актуализации.
в
в h h h
а а
а2 а·в a a a
a·h 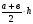
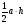
в
S2
R
R
r
а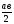
р (R2-r2) рR2 S1 + S2 + S3 +…
0
a
b
x
y
y=f(x)
R
r
S(x)
Q
x
H
рRr
убрать

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ